GPS整周模糊度
GPS整周模糊度

GPS整周模糊度GPS整周模糊度的计算与确定引⾔精密型GPS信号接收机⼀般都具有伪距和载波相位两种基本观测量。
相对于伪噪声码观测量⽽⾔,GPS载波相位观测量能提供⾮常精确的相对定位。
但由于GPS载波相位测量存在整周模糊数较难解算的问题,致使它在快速定位及导航中的应⽤受到了限制。
因此,快速⽽准确地求解GPS载波相位测量的整周模糊度就成了它在快速定位及导航中应⽤的关键问题。
整周模糊度求解的理论及其实⽤研究是近⼀、⼆⼗年的研究热点和难点。
许多学者提出了⼀些解算⽅法,其中双频P码伪距法、整周模糊度函数法、最⼩⼆乘搜索法和整周模糊度协⽅差法应⽤较⼴泛。
整周模糊度的确定是GPS载波相位测量中的关键问题,其原因如下:精确地、不⾜⼀周的相位与修复周跳后的正确整周记数只有在与正确的整周模糊度配合使⽤才有意义。
整周模糊度参数⼀旦出现问题,就将导致⼤量的卫地距出现系统性的粗差,从⽽严重影响定位的精度和可靠性,正确确定整周模糊度N是获得⾼精度定位结果的必要条件。
在⼤量对精确确定整周模糊度的计算研究中不断推出了新的计算算法。
⼏种整周模糊度的确定⽅法:(⼀)快速求解整周模糊度伪距双差⽅程经过线性化之后如下[2],(1)其中,ρ表⽰实际观测值与计算值之差,A表⽰系数阵,δx表⽰坐标增量,v表⽰模型误差和测量噪声,N(·)表⽰正态分布,QDΨ表⽰伪距测量的协⽅差阵。
由式(1),根据最⼩⼆乘原理可得(2)对于载波相位,其双差模型线性化之后可得[3](3)其中,l表⽰实际观测值与计算值之差,λ表⽰L1载波波长,N表⽰载波相位双差模糊度,w 表⽰模型误差和测量噪声,QDφ表⽰载波相位测量的协⽅差阵。
由式(2)、(3),可得整周模糊度的浮点解N^。
(4)由式(4)根据协因数传播定律,此时整周模糊度N^的协⽅差阵QN^为(5)其中表⽰坐标增量的协⽅差阵;表⽰后验⽅差系数;表⽰残差;n表⽰卫星数;u= rank(A)表⽰系数阵A的秩。
整周模糊度的确定

整周模糊度的确定确定整周未知数,是基于载波相位测量进行相对定位,必需解决的另一个关键问题。
精确和快速地求解整周未知数,对于确保相对定位的高精度,提高作业效率,开拓高精度动态定位新方法,都是极其重要的。
确定整周未知数的方法许多,若按解算所需时间的长短区分,可分为经典静态相对定位法和快速解算模糊度(整周未知数)法,而快速解算模糊度法又包括交换天线法,P码双频法、滤波法,搜寻法和模糊函数法等等;若按确定整周未知数时gps接收机的运动状态区分,又可分为静态法和动态法。
上述各种快速解算法皆属于静态法的范畴。
所谓动态法,就是GPS接收机在运动状态中完成求解整周未知数,它是实施高精度实时动态定位的基础。
一、经典静态相对定位法确定整周未知数这种方法是将作为待定的未知参数,在基线平差中与其它未知参数(如δXi、δYi、δZi等)一并求解的方法。
一般是由载波相位观测值组成双差分观测方程式,并进行方程式线性化,得到双差分误差方程式,则该方程式中包含有待定测站三个坐标改正数δXi、δYi、δZi和整周未知数的线性组合这四个未知数[此处]。
只要在已知测站和待定测站上同步观测不少于4颗卫星,则可平差解出整周未知数。
用这种方法一般需观测较长时间(几非常钟至几小时),但解算的精度最高,常用于静态相对定位中,尤其是用于长距离相对定位中。
在平差计算中,依据对的取值方式不同,可分为“整数解”(固定解)和“实数解”(浮动解)两种。
整数解是利用应当是整数的特性[也应为整数],将解得的▽▽N(t0)值进行凑整(凑成最接近的整数),然后将凑整后的作为已知量再代入双差分误差方程,重新平差,解算待定测站坐标改正数。
这种方法,只有当观测误差和外界误差对观测值影响较小,解得的比较接近整数的状况下才有效,此时,它可以提高解算结果的精度。
整数解常用于四、五十公里以下的基线的相对定位。
实数解当联测基线较长时,某些外界误差(如大气折射误差、卫星星历误差等)对基线两端点观测值的影响差别较大(即相关性不强),这时,在两测站间求差分时,就不能较好地消退或减弱其影响,它们在基线平差解算中将被汲取进待定测站坐标改正数和整周未知数中,这样解算出来的整周未知数一般偏离整数值较远,且其精度较低,误差可能大于半周,这时,我们不再考虑的整数特性,而取其实际解算值―实数解。
整周模糊度的解算
GPS精密定位周跳检测与修复(Cycle slip detection and repair)完整的载波相位是由初始整周模糊度N、计数器记录的整周数INT和接收机基频信号与收到到卫星信号的小于一周部分相位差Δφ。
Δφ能以极高的精度测定,但这只有在N和INT都正确无误地确定情况下才有意义。
卫星在观测中失锁后,造成接收机载波整周计数INT误差,这种现象称为周跳。
当重新捕获卫星后,周跳给计数器造成的偏差即为中断期间丢失的整周数,小周跳可以通过检测方法发现后并加以修复,大的周跳或较长时间的失锁,周跳不易修复,需要重新固定整周模糊度。
周跳的探测及修复对于用载波相位精密定位至关重要,成功的修复才能获得高精度的结果。
周跳产生的原因:1.卫星信号暂时阻断;2.仪器线路暂时故障;3.外界环境的突变干扰,如电离层、动态变化。
检测周跳的主要方法:1.屏幕扫描法观测值中出现周跳后。
相位观测值的变化率就不再连续。
凡曲线出现不规则的突然变化时,就意味着在相应的相位观测值中出现了整周跳变。
早期进行GPS相位测量的数据处理时,就是靠作业人员坐在计算机屏幕前依次对每个站、每个时段、每个卫星的相位观测值的变化率的图像进行逐段检查来探测周跳,然后再加以修复。
这种方法比较直观,在早期曾广泛使用。
但由于工作繁琐枯燥乏味,而且需反复进行,所以这种手工编辑方法目前正逐步被淘汰,而很少使用了。
2.高次差或多项式拟合法由于卫星和接收机间的距离在不断变化,因而载波相位测量的观测值INT+Δφ也随时间在不断变化。
但这种变化应是有规律的、平滑的。
周跳将破坏这种规律性。
根据这一特性就能将一些大的周跳寻找出来(尤其是对采样率较高的数据)。
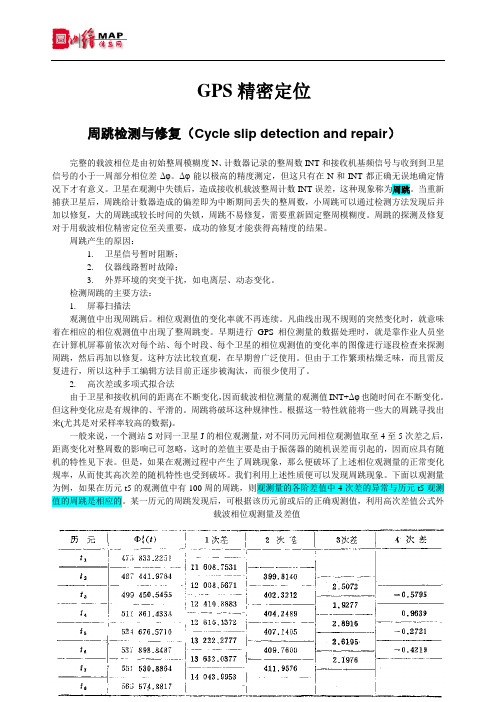
一般来说,一个测站S对同一卫星J的相位观测量,对不同历元间相位观测值取至4至5次差之后,距离变化对整周数的影响已可忽略,这时的差值主要是由于振荡器的随机误差而引起的,因而应具有随机的特性见下表。
但是,如果在观测过程中产生了周跳现象,那么便破坏了上述相位观测量的正常变化规率,从而使其高次差的随机特性也受到破坏。
第一课周跳的探测与修复整周模糊度的确定

正整周计数。这种方法实质上和上面介绍的高次差法是相 像的但便于计算 特点
由于四次差或五次差一般巳呈偶然误差特性无法再用函 数来加以拟合。所以用多项式拟合时通常也只需取至4—5 阶即可。观测值可以是真正的相位观测值也可以是经线性 组合后的虚拟观测值单差观测值和双差观测值
返回
载波相位测量的观测值N0+Int(ф) +Fr(ф)也随时 间在不断变化。但这种变化应是有规律的平滑的。 周跳将破坏这种规律性。 对于GPS卫星而言,当 求至四次差时,其值已趋向于零。残留的四次差 主要是由接收机的钟误差等因素引起的。
返回
< 3、多项式拟合法
原理 为了便于用计算机计算常采用多项式拟合的方法。即根
< 4、MW观测值法
返回
<
5、残差法
方法
根据平差后的残 差进行周跳的探测 与修复
特点
可以发现小周跳
返回
< 整周模糊度的确定
1、静态相对定位中的常用方法
取整法 置信区间法 模糊函数法
2、快速定位中的常用方法
走走停停法 快速静态定位法
3、动态相对定位中的常用方法
初始化法 实时解算模糊度法
返回
< 1、静态相对定位中的方法
周跳的探测与修复的方法
1、屏幕扫描法 2、高次差法 3、多项式拟合法 4、MW观测值法 5、残差法
返回
<
1、屏幕扫描法
原理 人工在屏幕上观察观测值曲线的变化是否
连续 特点
费时、只能发现大周跳。由于原始的载波 观测值变化很快,通常观察的 是某种观测值的 组合
返回
<
2、高次差法
高次差法的原理 由于卫星和接收机间的距离在不断变化,因而
改进GPS整周模糊度单历元求解方法(原创测绘论文)

改进GPS整周模糊度单历元求解方法(原创测绘论文)改进GPS整周模糊度单历元求解法在阳山金矿控制测量中的验证叶培1,1,安立宝2,2,庄景禾2,1(1,武警黄金第十二支队,四川成都610036,2,中国黄金集团阳山金矿有限公司,甘肃文县,746400)[摘要]快速准确地确定整周模糊度是进行高精度GPS测量的关键问题。
本文作者根据阳山金矿控制测量的自身特点,对刘宁等人提出的新GPS整周模糊度单历元求解法进行改进,简化模糊度搜索空间,增加单频机采集数据的算法,通过线性组合逆变化求取模糊度,以模糊度函数法进行真值的搜索,实现单历元解算。
在阳山矿区GPS控制测量中随机选取两条基线进行解算,从而证明此法的可行性和可靠性。
[关键词]整周模糊度;单历元;GPS;阳山矿区;模糊度搜索空间[文章编号]TD178[文献标识码]B[第一作者]叶培(1978-),男,2011年毕业于成都理工大学,获工程硕士学位,工程师,长期从事工程测绘工作。
Email:****************1、引言快速准确地确定整周模糊度是进行高精度GPS测量的关键问题,目前较为常见的模糊度解算方法有最小二乘搜索法、快速模糊度搜索的滤波法和最小二乘模糊度降相关平差法等。
这些方法各有优点,但也有其局限性,主要表现在需先进行相位周跳的探测与修复,且当卫星信号被遮挡时,需要对整周模糊度重新求解。
刘宁等人提出了一种新的GPS整周模糊度单历元求解法[1],不需要较为准确的先验约束信息便能得到高精度测量值。
但是各个测区,有其自身特点,这种方法是不是在每个测区都能得到较为可靠的精度,是一个值得探讨的问题。
武警黄金第十二支队从2000年开始,在甘肃省文县阳山金矿带陆续进行了大面积的GPS控制测量,其中D级控制测量面积为198平方千米,E级控制测量面积为87平方千米,整个GPS控制测量时间经历了近13年的时间。
阳山金矿测区属于秦岭造山带,地形复杂,切割较大,植被茂密,部分地区还有池塘和湖水对卫星信号起一定反射作用,而且2005年以前采集数据的机器还为单频机,如何根据测区自身特点来对这个新算法进行一定改进以提高GPS精度,就显得很有必要。
周跳和整周模糊度

周跳的来源、影响
周跳的来源
1、障碍物的遮挡造成信号中断; 2、卫星信号的信噪比过低; 3、接收机或卫星发生故障。
周跳的影响
在从发生周跳的历元开始的后续所有载波相位观测值 中引入一个相同大小的整周数偏差。
GPS测量原理及应用
周跳的探测与修复
周跳
• 探测出在何时发生了 周跳并求出丢失的整 周数,对中断后的整 周计数进行修正,并 恢复为正确的计数, 使这部分观测值仍可 用。
• 整数解——短基线测量
求初始解:确定基线向量 的实数解和整周未知数的 实数解 将整周未知数固定为整数 求固定解
• 实数解——长基线测量
基线较长,误差相关性减 弱,初始解的误差随之增 大,从而使整周未知数很 难固定,整数化的意义不 大。
GPS测量原理及应用
三差法
卫星间求一次差
单差 (直接观测值相减)
gps测量原理及应用周跳的探测与修复探测出在何时发生了周跳并求出丢失的整周数对中断后的整周计数进行修正并恢复为正确的计数使这部分观测值仍可双频观测值法电离层残差法gps测量原理及应用屏幕扫描法方法人工在屏幕上观察观测值曲线的变化是否连续
GPS测量原理及应用
GPS测量原理及应用
课程内容
• 第一部分:绪论 • 第二部分:周跳 • 第三部分:整周模糊度
GPS测量原理及应用
其他方法
• • • • • 交换天线法 双频P码伪距法 模糊度函数法 最小二乘搜索法 模糊度协方差法
GPS测量原理及应用
GPS测量原理及应用
载波相位测量的观测方程
f f f ft a ftb 1 2 N kj c c c
j k
GPS测量原理及应用
GPS整周模糊度解算方法

GPS 整周模糊度解算方法探讨一、为什么要解算GPS 整周模糊度?整周模糊度的确定是载波相位测量中的关键问题,这是因为:(1)精确的、不足1周的相位观测值()φr F 和修复周跳后的正确的整周计数()φInt 只有与正确的整周模糊度配合使用才有意义。
模糊度参数一旦出错,就将导致大量的卫地距出现系统性的粗差,从而严重损害定位的精度和可靠性。
正确确定整周模糊度N 是获得高精度定位结果的必要条件。
(2)在一般精度的GPS 定位中,定位所需的时间实际上就是正确确定整周模糊度所需要的时间。
快速确定整周模糊度对提高GPS 定位的作业效率具有极其重要的作用;对开拓GPS 定位技术的应用领域,将其推广应用到低等级控制测量和一般的工程测量等领域也具有极其重要的作用。
二、GPS 整周模糊度解算方法1、LAMBDA 法1993年荷兰Delft 大学的Teunissen 教授提出了最小二乘模糊度降相关平差法,简称LAMBDA 法。
该方法可缩小搜索范围,加快搜索过程,是目前快速静态定位中最成功的一种模糊度搜索方法。
LAMBDA 法的基本原理: (1)整数变换在LAMBDA 法中,并不直接对整数模糊度参数N 进行搜索,而是先对初始解中的实数模糊度参数⎪⎭⎫⎝⎛=∧∧∧∧n N N N N ,......,,21及其协因数阵∧N Q 进行整数变换:∧∧⋅=N Z z TZ Q Z Q NT z⋅⋅=∧∧式中Z 为整数变换矩阵。
整数变换具有以下特点:当N 为整数时,变换后的参数z 也为整数;反之,当z 为整数时,经逆变换后所得的()z Z N T⋅=-1也为整数。
整数变换并不是唯一的。
我们希望整数变换后所得到的新参数⎪⎭⎫⎝⎛=∧∧∧∧n z z z z ,......,,21之间的相关性能显著减小,其协因数阵∧z Q 中的非对角线元素5.0≤,模糊度参数的方差也能大幅度减小。
注意,整数变换指的是具有上述特性的一种数学变换方法,但并非只能对整数进行变换。
GPS整周模糊度的求解方法

用表示
,所以
式中L是
分解为LDLT得到的。
解出展开得
但由于
的结构比较差,故搜索范围较大,效率不高,所以又对
实行了Z转换,
Z为一整数矩阵,通过高斯整数变换得到。变换后的
为
其目的就是要使的结构比
的好。
2.2最优点判断标准
如上面所讲,LAMBDA方法的目的就是寻找
度的定位结果,必须预先解得模糊度的大小。很明显,当以载波相位观测量为依据,进行精密相对定位时,整周未知数的确定,是一个关键问题。
目前确定解算模糊度的方法有很多种,如经典待定系数法、快速模糊度分解法(FARA)、最小二乘搜索法、LAMBDA方法等,下面就几种模糊度解算方法进行阐述。
确定整周模糊度的传统方法:
为滤波器
输出,即模糊度的每历元的修正值,其他符号与前文相同。在滤波器中,方程(8)可以同时含有码伪距和载波相位观测信息。
2使用LAMBDA方法快速、准确解算整周模糊度
基于模糊度域的整周模糊度搜索方法,就是对模糊度估值域的搜索,即搜索程序直接或间接依赖于模糊度浮点解的方差阵的对角元素。如果存在一个可逆的整数变换矩阵,使得变换后的模糊度参数的方差阵的对角元素小于变换前的方差阵对应的对角元素,则搜索效率会大大提高。该观点首先被荷兰Delft大学的Teunissen教授表示为LAMBDA方法。2.1 LAMBDA方法解算整周模糊度可分为三个步骤1)标准最小二乘平差求基线和整周模糊度浮点解。2)整数最小二乘估计求整周模糊度固定解。3)求基线固定解。
当基线较长时,误差的相关性将降低,许多误差消除的不够完善。所以无论是基线向量还是整周未知数,均无法估计的很准确。在这种情况下再将整周未知数固定为某一整数往往无实际意义,所以通常将实数解作为最后解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
GPS整周模糊度的计算与确定引言精密型GPS信号接收机一般都具有伪距和载波相位两种基本观测量。
相对于伪噪声码观测量而言,GPS载波相位观测量能提供非常精确的相对定位。
但由于GPS载波相位测量存在整周模糊数较难解算的问题,致使它在快速定位及导航中的应用受到了限制。
因此,快速而准确地求解GPS载波相位测量的整周模糊度就成了它在快速定位及导航中应用的关键问题。
整周模糊度求解的理论及其实用研究是近一、二十年的研究热点和难点。
许多学者提出了一些解算方法,其中双频P码伪距法、整周模糊度函数法、最小二乘搜索法和整周模糊度协方差法应用较广泛。
整周模糊度的确定是GPS载波相位测量中的关键问题,其原因如下:精确地、不足一周的相位与修复周跳后的正确整周记数只有在与正确的整周模糊度配合使用才有意义。
整周模糊度参数一旦出现问题,就将导致大量的卫地距出现系统性的粗差,从而严重影响定位的精度和可靠性,正确确定整周模糊度N是获得高精度定位结果的必要条件。
在大量对精确确定整周模糊度的计算研究中不断推出了新的计算算法。
几种整周模糊度的确定方法:(一)快速求解整周模糊度伪距双差方程经过线性化之后如下[2],(1)其中,ρ表示实际观测值与计算值之差,A表示系数阵,δx表示坐标增量,v表示模型误差和测量噪声,N(·)表示正态分布,QDΨ表示伪距测量的协方差阵。
由式(1),根据最小二乘原理可得(2)对于载波相位,其双差模型线性化之后可得[3](3)其中,l表示实际观测值与计算值之差,λ表示L1载波波长,N表示载波相位双差模糊度,w 表示模型误差和测量噪声,QDφ表示载波相位测量的协方差阵。
由式(2)、(3),可得整周模糊度的浮点解N^。
(4)由式(4)根据协因数传播定律,此时整周模糊度N^的协方差阵QN^为(5)其中表示坐标增量的协方差阵;表示后验方差系数;表示残差;n表示卫星数;u= rank(A)表示系数阵A的秩。
由式(4)和(5),应用LAMBDA方法可以估计出整周模糊度的整数解。
LAMBDA方法搜索过程如下[4]:①方差阵Z变换(降相关变换);②浮点解分解整数部分和小数部分;③浮点解小数部分进行Z变换;④设置搜索提供的候选解个数;⑤计算搜索范围的大小(CHI2)的值;⑥求解浮点解小数部分进行Z变换后对应的固定解;⑦求解浮点解的固定解。
由于伪距的精度不高,此时求解出来的整周模糊度仍可能不正确,包含有一个偏差量δN。
因为模糊度Ni已经过LAMBDA方法搜索,该偏差量δN一般小于4周,所以,还需要第二个搜索过程。
以下采用FARA方法。
(6)其中,Ni表示LAMBDA方法求解的整周模糊度;δNi=βdiag(QN^)表示搜索空间;β表示置信度。
在第二个搜索过程中,根据FARA确定整周模糊度的准则知,因其组合数大大减少,所以能很快搜索出正确的整周模糊度。
(二)GPS短基线整周模糊度快速结算在很多情况下,位移的绝对值往往大于0.2 m,甚至可达0.5 m以上,例如悬索桥的变形。
在这些情况下,则不能直接应用DC算法。
为了扩大DC算法的应用范围,通过对载波相位进行组合,提出了一种适合大位移值的GPS整周模糊度直接解算方法。
该方法在位移值达到0.7 m时,仍可以直接解算GPS整周模糊度,并获得高精度的变形值。
将该方法推广到一般的GPS 短基线(基线长度小于等于10 km)定位的应用中,得到了GPS短基线定位时整周模糊度的准确快速算法。
在GPS变形监测网中,由于变形监测的基线比较短(基线长度小于等于10 km),在采用双差观测值后,可以大大消除卫星钟差、对流层、电离层延迟这些误差。
在基线小于10 km时,可以忽略这些误差的影响。
因此,可以解出整周模糊度:(1)式中, 为两历元两测站得到的相位整周数差之差; 为两历元两测站得到的相位差之差; 为两历元两测站得到的距离差之差[4]。
当监测点的位移小于0.1648 m时,位移对整周模糊度的影响小于等于半周。
这种利用监测点的位移为约束条件直接解算单历元变形量的方法就称为DC算法[1]。
保证L1和L2载波的整周模糊度N1和N2为整数的条件当位移值大到0.7 m时,如果还希望对整周模糊度的影响小于等于半周[5],并应用式(1)计算整周模糊度,载波相位的波长应为:(2)将位移值Δd=0.7 m代入式(2)。
当位移值Δd=0.7 m时,如果还希望对整周模糊度的影响小于等于半周[5],则载波相位的波长应为:(3)不同的载波相位组合观测值可以认为是不同波长和精度的载波相位观测值。
设φ1和φ2为一理想卫星发射的双频相位观测值,则可得到其组合观测值:(4)适当选取n和m,可以保证组合载波的波长大于等于0.808 3 m。
故按式(1)直接计算组合载波的整周模糊度,可使位移值对组合载波的整周模糊度的影响小于等于半周。
如此解出的组合载波的整周模糊度虽然比较准确,但不是所需要的最终结果。
所需要的最终结果是L1和L2的整周模糊度N1和N2。
如果还有一个波长大于0.808 3 m以上的载波相位组合观测值φs,应用式(1)也可以解得此组合的整周模糊度Ns。
有了线性组合的两个观测值的整周模糊度Nw和Ns,就可以通过解二元一次方程组,解出L1和L2载波的整周模糊度N1和N2,即(5)因为(6)式中,Nw、Ns、n1、m1、n2、m2均为整数。
故要保证由式(6)解得的N1、N2为整数,只需要保证:(7)即要求(8)式(8)就是通过解二元一次方程组,保证解算出的L1和L2载波的整周模糊度N1和N2为整数的条件式。
当使用宽巷与超宽巷组合的组合观测值来求解时,即,它们满足条件式(8),即.并且在满足式(8)中的所有线性组合观测值中,宽巷与超宽巷组合的噪声相对来说比较小。
而宽巷的波长λw=86.19 cm,超宽巷的波长λs=162.81 cm,它们都满足式(8)的条件。
所以采用宽巷与超宽巷组合作为求解L1和L2的整周模糊度的线性组合,既保证了整周模糊度的整数性质,在计算中又容易固定整周模糊度。
点位精度高于0.7m的初始坐标的获得因为一般的工程测量控制网,其基线长度都小于等于10 km,所以短基线模糊度的解算是GPS应用中最普遍的问题之一。
将DC算法用于短基线模糊度的解算,关键的问题是要得到点位精度高于0.7 m时各点的初始坐标。
由于GPS卫星轨道精度的不断提高(目前,精密星历为5 cm,普通星历为5 m),加之SA计划的取消,使得伪距单点定位的精度可达到5 m,伪距差分的精度已突破m级[9]。
为此,本文提出了利用伪距双差来获取初始坐标。
为了保证在快速静态定位中伪距差分的精度能满足0.7 m的要求,研制了专门的解算程序[10],并用武汉和深圳两地的实测数据进行了验算。
通过武汉和深圳的双GPS 数据(基线长度小于10 km),利用20min的伪距观测数据,用自编伪距双差程序与TGO解算的基线进行了比较分析,计算结果列于表1(前面10条基线为武汉地区采集的GPS数据计算的基线长度分量,后面6条为深圳地区采集的GPS数据计算的基线长度分量)。
由表1可以看出,利用20 min的伪距数据进行伪距双差,就可以保证基线长度的精度高于0.7 m。
(三)基于多历元递推最小二乘卡尔曼滤波方法的模糊度解算在GPS动态定位中,载波相位模糊度的解算多采用伪距信息和载波相位信息统一解算,其中伪距可以是一个历元的伪距观测信息,也可以是多个历元的伪距平滑信息,但是由于动态定位中目标点空间坐标在变化之中,载波相位信息目前常采用单个历元观测量,而放弃前续历元的载波相位观测信息。
如能有效地利用此多个历元的载波相位信息,将有助于模糊度的解算。
针对这个问题提出了同时使用多个历元的伪距信息和载波相位信息来解算载波相位模糊度。
与此同时,卡尔曼滤波技术在GPS导航定位中有着广泛应用,但是由于受到系统状态方程模型精度的限制,在cm级的差分GPS定位中,卡尔曼滤波使用的并不多。
但如果系统状态方程的模型精度很高,即仅对模糊度参数建模,滤波效果则大为改善。
GPS动态差分定位中的迭代最小二乘方法:由GPS双差线性观测方程:(1)式中,L为双差码伪距和载波相位观测矢量;B为差分GPS定位系数矩阵;dx为坐标未知数改正数向量;N为载波相位双差模糊度,具有整数特性;A为模糊度系数矩阵;D为观测矢量方差阵。
引入迭代最小二乘方法,可得到不含坐标未知数改正数向量dx的定位方程:(2)式中, ,I为单位阵, , ,其对应的法方程为:(3)由方程(3)可解得模糊度浮点解:方程(2)中不再具有坐标未知数改正数向量,只具有模糊度参数。
根据无周跳时前后历元模糊度不变的特性,可对多个历元的法方程(3)进行叠加,或者使用卡尔曼滤波方法,解得模糊度浮点解。
在模糊度浮点解的基础上,可使用动态模糊度搜索方法进行整数模糊度搜索。
对此相关文献研究较多[1],此处不再赘述。
基于递推最小二乘的卡尔曼滤波在正确探测并修复周跳的前提下,对于方程(2)模糊度浮点解的解算,既可以使用多历元法方程叠加方法,也可以使用卡尔曼滤波方法。
由于卡尔曼滤波方程便于编程实现,特别是在后文重新出现卫星的处理中非常方便,故本文使用后者。
由于方程(2)中只具有模糊度参数,所以滤波器状态方程的精度很高。
对于式(2),建立只含有模糊度参数的卡尔曼滤波器:(4)(5)式中,式(4)为状态方程,Nk为k时刻的模糊度向量;Nk+1为k+1时刻的模糊度向量;Qk为系统噪声阵,由于前后历元所对应的模糊度保持不变,故系统噪声阵可设为零。
式(5)为量测方程,是式(2)在k+1时刻的描述。
滤波器的广义滤波方程为:(6)(7)(8)(9)式中,P为系统方差阵;K为增益矩阵;I为单位阵; 为滤波器输出,即模糊度的每历元的修正值,其他符号与前文相同。
在滤波器中,方程(8)可以同时含有码伪距和载波相位观测信息。
参考文献:(1)邱蕾、花向红等,GPS短基线整周模糊度的直接解法,武汉大学学报-信息科学版,2009年1月第34卷第1期(2)刘立龙、唐诗华、文鸿雁,一种快速求解整周模糊度的方法,遥测遥控,2007年9月第28卷第5期(3)孙红星、付建红等,基于多历元递推最小二乘卡尔曼滤波方法的整周模糊度解算,武汉大学学报-信息科学版,2008年7月第33卷第7期。
