公司估值--第一讲-资本资产定价模型(CAPM)与贴现率估算
概述资本资产定价模型(CAPM)

概述资本资产定价模型(CAPM)一、引言(资本资产定价模型的理论源渊)资产定价理论源于马柯维茨(Harry Markowtitz)的资产组合理论的研究。
1952年,马柯维茨在《金融杂志》上发表题为《投资组合的选择》的博士论文是现代金融学的第一个突破,他在该文中确定了最小方差资产组合集合的思想和方法,开创了对投资进行整体管理的先河,奠定了投资理论发展的基石,这一理论提出标志着现代投资分析理论的诞生。
在此后的岁月里,经济学家们一直在利用数量化方法不断丰富和完善组合管理的理论和实际投资管理方法,并使之成为投资学的主流理论。
到了60年代初期,金融经济学家们开始研究马柯维茨的模型是如何影响证券估值,这一研究导致了资本资产定价模型(Capital Asset Price Model,简称为CAPM)的产生。
现代资本资产定价模型是由夏普(William Sharpe ,1964年)、林特纳(Jone Lintner,1965年)和莫辛(Mossin,1966年)根据马柯维茨最优资产组合选择的思想分别提出来的,因此资本资产定价模型也称为SLM模型。
由于资本资产定价模型在资产组合管理中具有重要的作用,从其创立的六十年代中期起,就迅速为实业界所接受并转化为实用,也成了学术界研究的焦点和热点问题。
二、资本资产定价模型理论描述资本资产定价模型是在马柯维茨均值方差理论基础上发展起来的,它继承了其的假设,如,资本市场是有效的、资产无限可分,投资者可以购买股票的任何部分、投资者根据均值方差选择投资组合、投资者是厌恶风险,永不满足的、存在着无风险资产,投资者可以按无风险利率自由借贷等等。
同时又由于马柯维茨的投资组合理论计算的繁琐性,导致了其的不实用性,夏普在继承的同时,为了简化模型,又增加了新的假设。
有,资本市场是完美的,没有交易成本,信息是免费的并且是立即可得的、所有投资者借贷利率相等、投资期是单期的或者说投资者都有相同的投资期限、投资者有相同的预期,即他们对预期回报率,标准差和证券之间的协方差具有相同的理解等等。
资本资产定价模型PPT课件

资产定价的随机过程
随机过程的基本概念
随机过程是描述一系列随机事件的数学模型,其中每个事件的发生都具有不确定性。在资产定价的上下文中,随 机过程通常用于描述资产价格的变动。
资本资产定价模型的随机过程
资本资产定价模型假设资产价格的变动遵循随机过程,并且这种变动与资产的预期回报和风险有关。通过建立适 当的随机过程模型,可以进一步研究资产价格的动态行为和风险特征。
发展历程
起源
资本资产定价模型起源于20世纪60年代,由经济学家威廉·夏普、 约翰·林特纳和简·莫辛共同发展。
发展
在随后的几十年中,CAPM经历了多次修订和完善,以适应金融市 场的变化。
应用
资本资产定价模型被广泛应用于投资组合管理、风险评估和资本预算 等领域。
发展历程
起源
资本资产定价模型起源于20世纪60年代,由经济学家威廉·夏普、 约翰·林特纳和简·莫辛共同发展。
发展
在随后的几十年中,CAPM经历了多次修订和完善,以适应金融市 场的变化。
应用
资本资产定价模型被广泛应用于投资组合管本资产定价模型用于确定投资 组合的风险和预期回报,帮助投 资者在风险和回报之间做出权衡。
风险评估
通过CAPM,投资者可以评估特 定资产或投资组合的风险,并与 其他资产或基准进行比较。
主要发现
是一种用于评估风险和预期回报之间关系的金融模型,主要用于投资组合管理 和风险评估。
CAPM的核心思想
资本的预期收益率由两部分组成,一部分是无风险利率,另一部分是风险溢价, 即风险超过无风险资产的部分。
目的和目标
目的
通过理解CAPM,投资者可以更准确 地评估投资的风险和预期回报,从而 做出更明智的投资决策。
(最新经营)如何估算贴现率doc15页

第一讲如何估算贴现率第一节资本资产定价模型(CAPM)与贴现率估算资本资产定价模型用不可分散化的方差来度量风险,将风险与预期收益联系起来,任何资产不可分散化的风险均可以用β值来描述,且相应地计算出预期收益率。
E(R)=R f+β(E[R m]-R f)其中:R f=无风险利率E(R m)=市场的预期收益率投资者所要求的收益率即为贴现率。
因此,从资本资产定价模型公式可以看出,要估算出贴现率要求以下变量是已知的:即期无风险利率(R f)、市场的预期收益率(E(R m))、资产的β值。
接下来几节,分别就如何估算无风险利率、市场预期收益率和β值进行讲解。
第二节如何估算无风险利率所谓无风险利率,是指投资者可以任意借入或者贷出资金的市场利率。
现阶段,符合理论要求的无风险利率有两个:回购利率、同业市场拆借利率。
我们倾向于推荐使用7天回购利率的30天或90天平均值,因为同业拆借市场对一般投资者是不开放的。
于美国等债券市场发达的国家,无风险利率的选取有三种观点:观点1:用短期国债利率作为无风险利率,用根据短期国债利率计算出的股票市场历史风险溢价收益率作为市场风险溢价收益率的估计值。
以这些数据为基础计算股权资本成本,作为未来现金流的贴现率。
例:使用即期短期国债利率的CAPM模型:百事可乐企业1992年12月,百事可乐企业的β值为1.06,当时的短期国债利率为3.35%,企业股权资本成本的计算如下:股权成本=3.35%+(1.06×6.41%)=10.14%我们可以使用10.14%的股权资本作为红利或现金流的贴现率来计算百事可乐企业股票的价值。
观点2、使用即期短期政府债券与市场的历史风险溢价收益率计算第一期(年)的股权资本成本。
同时利用期限结构中的远期利率估计远期的无风险利率,作为未来时期的股权资本成本。
例:使用远期利率的CAPM模型:百事可乐企业假设即期国债利率为3.35%,利率的期限结构中的1年期远期利率如下:1年远期利率=4.0%;2年远期利率=4.4%;3年远期利率=4.7%;4年远期利率=5.0%.使用这些远期利率计算股权资本成本:第一年的股权成本=3.35%+(1.06×6.4%1)=10.14%第二年的股权成本=4%+(1.06%×6.1%)=10.47%第三年的股权成本=4.4%+(1.06×5.9%)=10.65%第四年的股权成本=4.7%+(1.06×5.8%)=10.85%第五年的股权成本=5%+(1.06×5.7%)=11.04%注意:于上面的计算中,期限越长,市场风险溢价收益率越低。
公司估值--第一讲-资本资产定价模型(CAPM)与贴现率估算

第一节资本资产定价模型(CAPM)与贴现率估算资本资产定价模型用不可分散化的方差来度量风险,将风险与预期收益联系起来,任何资产不可分散化的风险都可以用β值来描述,并相应地计算出预期收益率。
E(R)=Rf+β(E[Rm]-Rf)其中:Rf =无风险利率E(Rm)=市场的预期收益率投资者所要求的收益率即为贴现率。
因此,从资本资产定价模型公式可以看出,要估算出贴现率要求以下变量是已知的:即期无风险利率(Rf)、市场的预期收益率(E(Rm))、资产的β值。
接下来几节,分别就如何估算无风险利率、市场预期收益率和β值进行讲解。
第二节如何估算无风险利率所谓无风险利率,是指投资者可以任意借入或者贷出资金的市场利率。
现阶段,符合理论要求的无风险利率有两个:回购利率、同业市场拆借利率。
我们倾向于推荐使用7天回购利率的30天或90天平均值,因为同业拆借市场对一般投资者是不开放的。
在美国等债券市场发达的国家,无风险利率的选取有三种观点:观点1:用短期国债利率作为无风险利率,用根据短期国债利率计算出的股票市场历史风险溢价收益率作为市场风险溢价收益率的估计值。
以这些数据为基础计算股权资本成本,作为未来现金流的贴现率。
例:使用即期短期国债利率的CAPM模型:百事可乐公司1992年12月,百事可乐公司的β值为1.06,当时的短期国债利率为3.35%,公司股权资本成本的计算如下:股权成本=3.35%+(1.06×6.41%)=10.14%我们可以使用10.14%的股权资本作为红利或现金流的贴现率来计算百事可乐公司股票的价值。
观点2、使用即期短期政府债券与市场的历史风险溢价收益率计算第一期(年)的股权资本成本。
同时利用期限结构中的远期利率估计远期的无风险利率,作为未来时期的股权资本成本。
例:使用远期利率的CAPM模型:百事可乐公司假设即期国债利率为3.35%,利率的期限结构中的1年期远期利率如下:1年远期利率=4.0%;2年远期利率=4.4%;3年远期利率=4.7%;4年远期利率=5.0%.使用这些远期利率计算股权资本成本:第一年的股权成本=3.35%+(1.06×6.4%1)=10.14%第二年的股权成本=4%+(1.06%×6.1%)=10.47%第三年的股权成本=4.4%+(1.06×5.9%)=10.65%第四年的股权成本=4.7%+(1.06×5.8%)=10.85%第五年的股权成本=5%+(1.06×5.7%)=11.04%注意:在上面的计算中,期限越长,市场风险溢价收益率越低。
资本资产定价模型(CAPM)教学讲义

10/22/2020
1
6.1 资本资产定价模型(CAPM)
❖ 资本资产定价模型(Capital Asset Pricing Model,CAPM)是由美国Stanford大学教授夏 普等人在马克维茨的证券投资组合理论基础上 提出的一种证券投资理论。
❖ CAPM解决了所有的人按照组合理论投资下,资 产的收益与风险的问题。
5
收益rp
rf
非有效
10/22/2020
不可行
风险σp
6
6.1.2 CAPM的基本假设
CAPM模型是建立在一系列假设基础之上的。 设定假设的原因在于:由于实际的经济环境 过于复杂,以至我们无法描述所有影响该环 境的因素,而只能集中于最重要的因素,而 这又只能通过对经济环境作出的一系列假设 来达到。
风险基金=市场组合(Market portfolio):与整个市场上风险证券比 例一致的资产组合。对股票市场而言,就 是构造一个包括所有上市公司股票,且结 构相同的基金(如指数基金)。
因为只有当风险基金等价与市场组合时,
才能保证:(1)全体投资者购买的风险
证券等于市场风险证券的总和——市场均
10/22/2020
(1)
10/22/2020
4
组合的标准差为
一种风险资产与无风险资产构 成的组合,其标准差是风险资
产的权重与标准差的乘积。
p w11
(2)
由(1)和(2)可得
rp
p 1
r1
(1
p 1
)rf
=rf
(r1 rf
1
)
p
可以发现这是一条以rf
为截距,以
r1
rf
CAPM资本资产定价模型

资本资产定价模型(Capital Asset Pricing Model简称CAPM)资本资产定价模型(CapitalAssetPricingModel简称CAPM)是由美国学者夏普(William Sharpe)、林特尔(John Lintner)、特里诺(Jack Treynor)和莫辛(JanMossin)等人在资产组合理论的基础上发展起来的,是现代金融市场价格理论的支柱,广泛应用于投资决策和公司理财领域。
一、资本资产定价模型资本资产定价模型就是在投资组合理论和资本市场理论基础上形成发展起来的,主要研究证券市场中资产的预期收益率与风险资产之间的关系,以及均衡价格是如何形成的.CAPM是建立在马科威茨模型基础上的,马科威茨模型的假设自然包含在其中:1、投资者希望财富越多愈好,效用是财富的函数,财富又是投资收益率的函数,因此可以认为效用为收益率的函数。
2、投资者能事先知道投资收益率的概率分布为正态分布。
3、投资风险用投资收益率的方差或标准差标识。
4、影响投资决策的主要因素为期望收益率和风险两项。
5、投资者都遵守主宰原则(Dominancerule),即同一风险水平下,选择收益率较高的证券;同一收益率水平下,选择风险较低的证券。
CAPM的附加假设条件:6、可以在无风险折现率R的水平下无限制地借入或贷出资金。
7、所有投资者对证券收益率概率分布的看法一致,因此市场上的效率边界只有一条。
8、所有投资者具有相同的投资期限,而且只有一期。
9、所有的证券投资可以无限制的细分,在任何一个投资组合里可以含有非整数股份。
10、买卖证券时没有税负及交易成本。
11、所有投资者可以及时免费获得充分的市场信息。
12、不存在通货膨胀,且折现率不变。
13、投资者具有相同预期,即他们对预期收益率、标准差和证券之间的协方差具有相同的预期值。
上述假设表明:第一,投资者是理性的,而且严格按照马科威茨模型的规则进行多样化的投资,并将从有效边界的某处选择投资组合;第二,资本市场是完全有效的市场,没有任何磨擦阻碍投资。
公司估值--第一讲-资本资产定价模型(CAPM)与贴现率估算

第一节资本资产定价模型( CAPM )与贴现率估算资本资产定价模型用不可分散化的方差来度量风险,将风险与预期收益联系起来,任何资产不可分散化的风险都可以用B值来描述,并相应地计算出预期收益率。
E (R)=Rf+ B ( E[Rm]-Rf )其中:Rf =无风险利率E( Rm) =市场的预期收益率投资者所要求的收益率即为贴现率。
因此,从资本资产定价模型公式可以看出,要估算出贴现率要求以下变量是已知的:即期无风险利率 ( Rf)、市场的预期收益率(E ( Rm))、资产的B值。
接下来几节,分别就如何估算无风险利率、市场预期收益率和B值进行讲解。
第二节如何估算无风险利率所谓无风险利率,是指投资者可以任意借入或者贷出资金的市场利率。
现阶段,符合理论要求的无风险利率有两个:回购利率、同业市场拆借利率。
我们倾向于推荐使用7天回购利率的30天或90 天平均值,因为同业拆借市场对一般投资者是不开放的。
在美国等债券市场发达的国家,无风险利率的选取有三种观点:观点1:用短期国债利率作为无风险利率,用根据短期国债利率计算出的股票市场历史风险溢价收益率作为市场风险溢价收益率的估计值。
以这些数据为基础计算股权资本成本,作为未来现金流的贴现率。
例:使用即期短期国债利率的CAPM 模型:百事可乐公司1992年12月,百事可乐公司的 B值为1.06,当时的短期国债利率为 3.35%,公司股权资本成本的计算如下:股权成本=3.35%+(1.06 >6.41%)=10.14%我们可以使用10.14%的股权资本作为红利或现金流的贴现率来计算百事可乐公司股票的价值。
观点2、使用即期短期政府债券与市场的历史风险溢价收益率计算第一期(年)的股权资本成本。
同时利用期限结构中的远期利率估计远期的无风险利率,作为未来时期的股权资本成本。
例:使用远期利率的CAPM 模型:百事可乐公司假设即期国债利率为 3.35%,利率的期限结构中的 1 年期远期利率如下:1年远期利率=4.0% ; 2年远期利率=4.4%;3年远期利率=4 .7%; 4年远期利率=5 .0%. 使用这些远期利率计算股权资本成本:第一年的股权成本=3 .35% +(1 .06 >6.4%1) =10.14 %第二年的股权成本=4% + (1.06%X6.1%)=10.47%第三年的股权成本=4 .4%+(1.06 >5.9%)=10.65%第四年的股权成本= 4.7%+(1.06 >5.8%)=10.85%第五年的股权成本= 5%+(1.06> 5.7%)=11.04% 注意:在上面的计算中,期限越长,市场风险溢价收益率越低。
资本资产定价模型CAPM.pptx
0.0205
14.3%
债券基金
回报率 离标差准平差方
17%
1.00%
7%
0.00%
-3%
1.00%
7.00%
0.0067
8.2%
14.3% 0.0205
9
第10页/共73页
协方差
衡量资产同步变动的程度
考虑如下的乘积:
[r股票(s)-E(r股票)][r债券(s)-E(r债券)]
协方差的定义
Cov(r股票,r债券) = S P(s)[r股票(s)-E(r股票)][r债券(s)-E(r债
26
第27页/共73页
10.4 两个资产的有效集
股票在组合的比率
0% 5% 10% 15% 20% 25% 30% 35% 40% 45% 50.00% 55% 60% 65% 70% 75% 80% 85% 90% 95% 100%
风险
8.2% 7.0% 5.9% 4.8% 3.7% 2.6% 1.4% 0.4% 0.9% 2.0% 3.08% 4.2% 5.3% 6.4% 7.6% 8.7% 9.8% 10.9% 12.1% 13.2% 14.3%
0.00%
-3%
1.00%
7.00%
0.0067
8.2%
2.05% 1 (3.24% 0.01% 2.89%) 3
8
第9页/共73页
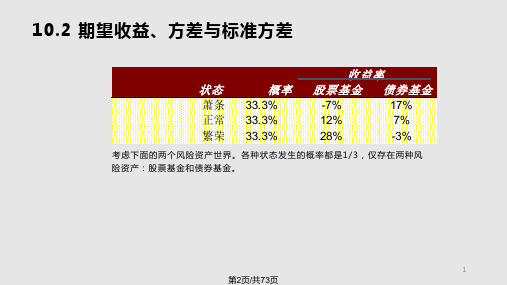
10.2 期望收益、方差与标准方差
状态
萧条 正常 繁荣
期望收益 方差 标准差
股票基金
回报率 离标差准平差方
-7%
3.24%
12%
0.01%
28%
2.89%
11.00%
24
第25页/共73页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节资本资产定价模型(CAPM)与贴现率估算资本资产定价模型用不可分散化的方差来度量风险,将风险与预期收益联系起来,任何资产不可分散化的风险都可以用β值来描述,并相应地计算出预期收益率。
E(R)=Rf+β(E[Rm]-Rf)其中:Rf =无风险利率E(Rm)=市场的预期收益率投资者所要求的收益率即为贴现率。
因此,从资本资产定价模型公式可以看出,要估算出贴现率要求以下变量是已知的:即期无风险利率(Rf)、市场的预期收益率(E(Rm))、资产的β值。
接下来几节,分别就如何估算无风险利率、市场预期收益率和β值进行讲解。
第二节如何估算无风险利率所谓无风险利率,是指投资者可以任意借入或者贷出资金的市场利率。
现阶段,符合理论要求的无风险利率有两个:回购利率、同业市场拆借利率。
我们倾向于推荐使用7天回购利率的30天或90天平均值,因为同业拆借市场对一般投资者是不开放的。
在美国等债券市场发达的国家,无风险利率的选取有三种观点:观点1:用短期国债利率作为无风险利率,用根据短期国债利率计算出的股票市场历史风险溢价收益率作为市场风险溢价收益率的估计值。
以这些数据为基础计算股权资本成本,作为未来现金流的贴现率。
例:使用即期短期国债利率的CAPM模型:百事可乐公司1992年12月,百事可乐公司的β值为1.06,当时的短期国债利率为3.35%,公司股权资本成本的计算如下:股权成本=3.35%+(1.06×6.41%)=10.14%我们可以使用10.14%的股权资本作为红利或现金流的贴现率来计算百事可乐公司股票的价值。
观点2、使用即期短期政府债券与市场的历史风险溢价收益率计算第一期(年)的股权资本成本。
同时利用期限结构中的远期利率估计远期的无风险利率,作为未来时期的股权资本成本。
例:使用远期利率的CAPM模型:百事可乐公司假设即期国债利率为3.35%,利率的期限结构中的1年期远期利率如下:1年远期利率=4.0%;2年远期利率=4.4%;3年远期利率=4.7%;4年远期利率=5.0%.使用这些远期利率计算股权资本成本:第一年的股权成本=3.35%+(1.06×6.4%1)=10.14%第二年的股权成本=4%+(1.06%×6.1%)=10.47%第三年的股权成本=4.4%+(1.06×5.9%)=10.65%第四年的股权成本=4.7%+(1.06×5.8%)=10.85%第五年的股权成本=5%+(1.06×5.7%)=11.04%注意:在上面的计算中,期限越长,市场风险溢价收益率越低。
这说明与相对即期国债利率的风险溢价收益率相比,相对远期利率的股票市场的历史风险溢价收益率较低。
观点3:用即期的长期国债利率作为无风险利率,用根据长期国债利率计算出的股票市场历史风险溢价收益率作为市场风险溢价收益率的估计值。
以这些数据为基础计算股权资本成本,作为未来现金流的贴现率。
例:使用即期长期国债利率为7%,在长期国债而不是短期国债的基础之上计算市场的风险溢价收益率。
从1926年到1990年的市场风险溢价怍益率为5.5%。
已知百事可乐公司股票的β值为1.06,则其股权资本成本为:以上给出的三种观点中,三种观点中哪一种最好?从理论上与直观上来说观点都是合理的。
第一种观点认为CAPM是单时期的风险收益模型,即期的短期国债利率是未来短期利率的合理预期。
第二个观点着重于远期利率在预测未来利率中存在的优势,第三种观点认为长期国债与被估价资产具有相同的到期期限。
在实际中,当利率的期限结构与历史上短期利率与长期利率的关系相同,且β值趋近于1的时候,这三种方法计算的结果是相同的。
当期限结构与历史数据发生偏离,或者β远不等于1时,这三种方法计算的结果不相同。
如果收益率曲线向上倾斜的程度较大,则使用长期利率得到的贴现率较高,从而会造成价值的低估。
如果收益率曲线向上倾斜的程度较小甚至出现向下倾斜,则结论正好相反。
第三节如何估算预期市场收益率或者风险溢价CAPM中使用的风险溢价是在历史数据的基础上计算出的,风险溢价的定义是:在观测时期内股票的平均收益率与无风险证券平均收益率的差额,即(E[Rm]-Rf)。
目前国内的业界中,一般将(E[Rm]-Rf)视为一个整体、一个大体固定的数值,取值在8—9%左右。
理论上,由于无风险利率已知,只需要估算出预期市场收益率即可。
在具体的计算时我们面临两个问题:样本的观测期应该是多长?是使用算术平均值还是几何平均值?人们对于使用算术平均值还是几何平均值有很大的争论。
主张使用算术平均值的人认为算术平均值更加符合CAPM期望一方差的理论框架,并且能对下一期的收益率做出较好的预测。
主张使用几何平均值的人认为几何平均值考虑了复利计算方法,是对长期平均收益率的一种较好的估计,这两种方法所得到的溢价利率可能会有很大的差异。
表1是根据美国股票和债券的历史数据计算的溢价利率。
表1:(美国市场)风险溢价水平(%)历史时期对短期国债的风险溢价对长期国债的风险溢价算术平均值几何平均值算术平均值风何平均值1926-1990 8.41 6.41 7.21 5.501962-1990 4.10 2.95 3.92 3.251981-1990 6.05 5.38 0.13 0.19用几何平均值计算得到的收益率一般比算术平均值要低,因为在估价时我们是对一段较长时间内的现金流进行贴现,所以几何平均值对风险溢价的估计效果更好。
表2列出了世界各国的风险洋价收益率,从表中可见欧洲市场(不包括英国)股票相对国库券的风险溢价收益率没有美国和日本高,决定风险溢价收益率的因素有以下三点:(a)宏观经济的波动程度:如果一个国家的宏观经济容易发生波动,那么股票市场的风险溢价收益率就较高,新兴市场由于发展速度较快,经济系统风险较高,所以风险溢价水平高于发达国家的市场。
(b)政治风险:政治的不稳定会导致经济的不稳定,进而导致风险溢价收益率较高。
(c)市场结构:有些股票市场的风险溢价收益率较低是因为这些市场的上市公司规模较大,经营多样化,且相当稳定(比如德国与瑞士),一般来说,如果上市公司普遍规模较小而且风险性较大,则该股票市场的风险溢价收益率会较大。
表2:世界各国的股票市场风险溢价收益率(%)。
1970-1990年国家股票政府债券风险溢价收益率澳大利亚 9.60 7.35 2.25加拿大 10.50 7.41 3.09法国 11.90 7.68 4.22德国 7.40 6.81 0.59意大利 9.40 9.06 0.34日本 13.70 6.96 6.74荷兰 11.20 6.87 4.33瑞士 5.30 4.10 1.20英国 14.70 8.15 6.25美国 10.00 6.18 3.82以美国股票市场 5.50%的风险溢价收益率作基准,我们发现比美国市场风险性高的市场风险溢价收益率也较大,比美国市场风险性低的市场风险溢价收益率也较低。
金融市场的特点对政府债券的风险溢价收益率有政治风险的正在形成中的市场(南美、东欧) 8.5%发展中的市场(除日本外的亚洲市场、墨西哥) 7.5%规模较大的发达市场(美国、日本、英国) 5.5%规模较小的发达市场(除德国与瑞士外的西欧市场) 4.5%-5.5%规模较小,经济稳定的发达市场(德国、瑞士) 3.5%-4%第四节如何估算β值关于β值的估算,因首次公发与增发项目类型不同估算方法不尽相同。
一、增发项目β值的估算对于增发项目来说,其已经是上市公司、股票已经上市交易,对其β值估算的一般方法是对股票收益率(R1)与市场收益率(Rm)进行回归分析:R1=a+bRm其中:a=回归曲线的截距b=回归曲线的斜率=cov(R1 Rm)/σ2m回归方程中得到的R2是一个很有用的统计量。
在统计意义上R2是衡量回归方程拟和程度的一个标准,在经济意义上R2表示了风险在公司整个风险中所占的比例,(1-R2)表示了公司特有风险在公司整个风险中所占的比例。
例:估计CAPM的风险参数:Intel公司Intel公司是一家世界著名的以生产个人电脑芯片为主的公司。
下面是Intel公司回归方程的统计数据,从1989年1月到1993年12月Intel公司与S&P500公司月收益率的比较。
(a)回归曲线的斜率=1.39;这是Intel公司的β值,是根据1989年到1993年的历史数据计算得到的。
使用不同的回归期,或者相同的回归期但时间间隔不同(以周或天为时间间隔)进行计算,都会得出不同的β值。
(b)回归方程的R2=22.90%,这表明Intel公司整体风险的22.90%来自于市场风险(利率风险,通货膨胀风险等等),77.10%来自于公司特有风险。
因为后者是可以通过分散投资消除的,所以在CAPM中没有反映出来。
在进行回归分析时要考虑四个问题。
第一个是回归期限的长度,估计期越长,可使用的数据越多,但是公司本身的风险特征可能已经随时间的推移而发生了改变。
例如:我们使用1980年到1992年的数据估计苹果计算机(Apple Computer)公司的β值,可使用的数据量较大,但是得出的β值估计值要比真实值高,因为苹果计算机公司在20世纪80年代初规模较小,风险较大。
第二个是回归分析所使用数据的时间隔,我们可以使用以年、月、星期、天,甚至一天中的某一段时间为收益率的单位。
以天或更小的时间单位作为收益率的单位进行回归分析可以增加观察值的数量,但是,由于在短时间单位内公司股票的交易量可能为零,从而导致β值估计中出现严重误差。
例如,例用每天收益率来估计小型公司的β值时,可能会因为小型公司在一天内无任何交易而命名估计出的β值偏低。
使用以星期或月为时间单位的收益率能够显著减少这种由于无交易量而导致的β值估计误差。
第三个问题是回归分析中市场收益率的选择。
估计β值的一般主方法是使用公司股票所在交易市场的收益率。
因此,在估计德国公司股票β值时用法兰克富DAX指数收益率,在估计英国公司股票β值时采用伦敦金融时报股票指数(FTSE)收益率,在估计日本公司股票的β值时采用日经指数(Nikkei)收益率,在估计美国公司股票的β值时使用纽约股票交易所指数(NYSE)收益率。
第四个总是是回归分析得到的β值是否应该加以调整,以反映回归分析中可能的误差和β值偏离平均值(行业或整个市场)的程度。
许多公布的β值都使用了一种根据回归分析中β估计值的标准差将β值向1的方向调整的统计方法——标准差越大,调整的幅度越大,这些方法在使用每天收益率估计β值时效果最显著,收益率时间单位越长,效果越不明显。
β值的决定因素。
公司的β值由三个因素决定:公司所处的行来、公司的经营杠杆比率和公司的财务杠杆比率。
行业类型:β值是衡量公司相对于市场风险程度的指标。
