曲线要素计算表
曲线计算公式

一、曲线要素计算已知:JDZH 、JDX 、JDY 、R 、L S1、L S2、L H 、T 、A 1、A 2(L H =L S1+L S2+圆曲线长)1、求ZH 点(或ZY 点)坐标及方位角⎪⎩⎪⎨⎧-=-=-=11sin cos AT JDY ZHY A T JDX ZHX TJDZH ZHZH 2、求HZ 点(或YZ 点)坐标及方位角⎪⎩⎪⎨⎧+=+=+-=22sin cos AT JDY HZY A T JDX HZX L T JDZH HZZH H3、求解切线长T 、外距E 、曲线长L(1)圆曲线⎪⎩⎪⎨⎧=-==180/)1)2/cos(/1()2/tan(απααR L R E R T (2)缓圆曲线 )2/(2/)2/cos(/)(2180/)21()2/tan()(020R l l l Rl l R p R E l R L qp R T s s s HsH H ===⎪⎩⎪⎨⎧-+=+⨯-=+⨯+=ββαπβα时当其中 二、直线上各桩号坐标及方位角计算 已知:ZH 、X 、Y 、A ⎪⎩⎪⎨⎧+=+==-=A L Y DY A L X DX A T ZH DZH L sin cos 三、第一缓和曲线上各桩号点坐标及方位角计算 已知:ZHZH 、ZHX 、ZHY 、A 1、R 、L S1、i (Z+1Y-1) ⎪⎩⎪⎨⎧⨯-+=⨯++=⨯⨯-==-=-=1111121132125cos sin sin cos /180)2/()6/()40/(Ay i A x ZHY DY A y i A x ZHX DX Rl l i A T Rl L y l R L L x ZHZH DZH L s s s π四、圆曲线上各桩号点坐标及方位角计算已知:ZHZH 、ZHX 、ZHY 、A 1、R 、L S1、i (Z+1Y-1)⎪⎩⎪⎨⎧⨯-+=⨯++=⨯+⨯-=⎪⎩⎪⎨⎧=-==++-=-++=--=1111121231110211231111cos sin sin cos /180)/2/(24/240/2/2/24/)]/2/cos(1[240/2/)/2/sin(Ay i A x ZHY DY A y i A x ZHX DX R L R l i A T R l p R l l q R l R l R L R l R y R l l R L R l R x ls ZHZH DZH L s s s s s s s s s s πβ其中五、第二缓和曲线上个桩号坐标及方位角计算 已知:HZZH 、HZX 、HZY 、A2、R 、L S2、i (Z+1Y-1) ⎪⎩⎪⎨⎧⨯--=⨯+-=⨯⨯+==-=-=2222222232225cos sin sin cos /180)2/()6/()40/(Ay i A x HZY DY A y i A x HZX DX Rl l i A T Rl L y l R L L x DZHHZZH L s s s π六、边桩坐标求解 已知:DZH 、X 、Y 、T 、BZJL (Z+Y-)、DLJJ 、N (距中桩距离,左正右负)⎪⎩⎪⎨⎧-=-=+=T N Y BDY T N X BDX T T sin cos α七、纵断面高程计算(1) 直线段上高程计算 已知:直线上任一点桩号(ZH )、高程(H )、纵坡(i ))(*ZH DZH i H DH -+=(2) 竖曲线上高程计算已知:竖曲线起点桩号(ZH )、起点高程(H )、竖曲线半径R 、起点坡度(i )、k (凸曲线+1、凹曲线-1) )2/(2R l k il H DH ZHDZH l ⨯-+=-=注:JDZH 、JDX 、JDY :交点桩号、交点X 、Y 坐标R 、L S1、L S2:半径、缓和曲线1、缓和曲线2LH :缓和曲线1长 +圆曲线长+ 缓和曲线2长 A1、A2:方位角1、方位角2 T :在曲线要素中代表切线长;在坐标计算中代表被求解点的坐标方位角。
(完整版)平曲线要素计算

一、路线转角、交点间距的计算(一)在地形图上量出路线起终点及各路线交点的坐标:QD 23810,27180、JD1 23996,26977 、JD 224684,26591、 JD3248480,25885、JD4 25350,25204 、ZD2606225783,(二)计算公式及方法设起点坐标为 QD X0,Y0,第 i 个交点坐标为 JD i X i ,Y i , i1,2,3,4, 则坐标增量 DX X i X i 1, DY Y i Y i 1交点间距 D(DX )22 DY象限角arctanDYDX方向角 A 是由象限角计算的:象限DX DY A象限DX DY A Ⅰ++AⅢ--A180o Ⅱ-+ A 180oⅣ+-A360o转角i A i Ai 11.QD与 JD1之间:坐标增量 DX X1X 0 =2396623810=186 0DY Y1Y026977271802030交点间距 D(DX )2DY 218622032275.33m象限角arctan DY arctan20347.502 oDX186方向角 A0360o360o47.502o312.498o 2.JD1与 JD 2之间:坐标增量 DX X 2X1=2468423966=688 0DY Y2Y126591269773860交点间距 D(DX )2268823862DY788.89 m象限角arctanDYarctan386 29.294 oDX688方向角 A 1 360o360o 29.294o 330.706o 转角 1 =A 1 A 0 330.706o 312.498o 18.208o3. JD 2 与JD 3之间:坐标增量 DXX 3 X 2 =24840 24684=156 0DYY 3 Y 2 25885 26591706 0交点间距 D(DX )221562 706 2DY723.03m象限角arctanDYarctan706 77.54oDX156方向角 A 2 360o360o 77.54o 282.46o转角 2 =A 2 A 1 282.46o 330.706o 48.246 o4. JD 3与 JD 4 之间:坐标增量 DXX 4 X 3 =25350 24840=510 0DY Y 4 Y 3 25204 25885681 0交点间距 D(DX )225102681 2DY850.8m象限角arctan DYarctan 51053.171oDX681方向角 A 3 360o360o 53.171o306.829o 转角 3 =A 3 A 2 306.829 282.4624.369o5. JD 4 与 ZD 之间:坐标增量 DXX X 4 =26062 25350=712 0DYYY 4 2578325204579 0交点间距 D (DX )2 27122 5792 917.706mDY象限角arctanDYarctan57939.118 oDX712方向角 A 039.118o转角 4 =A 4 A 3 39.118o 312.498o 92.289o二、各平曲线要素的计算( 一) JD 1曲线要素计算取R 800m ,设计速度为 60km/ h ,JD1桩号为K0+275.33,转角1.缓和曲线长度 L S,则:L SV 30.0366030.0369.72(m)R800L SV60350(m) 33.63.6L S R~ R800~ 80088.89 ~ 800(m) 99取整数,采用缓和曲线长120m(《公路工程技术标准》规定:V 最小缓和曲线长度为50m ).2.圆曲线内移值 RL2S L4S120212040.75(m)R2688 (R)324 8002688 (800) 324R3.总切线长T hL S L3S120120359.989(m)先求 q240R2224080022所以 T h (R R) tan q(80018.20859.989 188.31(m)0.75) tan224.曲线总长度 L hL S=0.0752RL h ( 2 )R 2L S?R+L S 374.22(m)1801805.五个基本桩号JD 1K0+274.33)T h188.31ZH 1K 0+087.0218.208o60 km h 时,)L SHY1)( L h 2L S )YH1)L SHZ 11L h)2QZ1120.00K0+207.02134.22 K0+341.24120.00 K0+461.24187.11 K0+274.13E h ( R R)sec R (8000.75sec 18.208800 10.97(m)22超距 D2T L h 2 188.31374.22 2.4(m)。
圆曲线要素及计算公式

第二章圆曲线要素及计算公式
如图2-1所示,两相邻直线偏角(线路转向角)为,选定其
图 2-1
连接曲线圆曲线的半径为R,这样,圆曲线和两直线段的切点位置ZY点、YZ点便被确定下来,我们称为对圆曲线相对位置起控制作用的直圆点ZY、圆直点YZ和曲中点QZ为圆曲线三主要点。
我们称R、α以及具体体现三主要点几何位置的切线长T、曲线长L、外矢距E和切曲差(切线长和曲线长之差)D为曲线6要素。
只要知道了曲线6要素,便可于实地测放出圆曲线。
现将圆曲线的元素列下:
:转向角(实地测出)
R:曲率半径(设计给出)
T:切线长(计算得出)
L:曲线长(计算得出)
D:切曲差(计算得出)
偏角是在线路祥测时测放出的,圆曲线半径R是在设计中根据线路的等级以及现场
地形条件等因素选定的,其余要素可根据以下公式计算:。
曲线要素等计算公式表格

左边桩距 0.000 0.000 0.000 0.000 0.000 0.000 20.900 0.000 20.000 20.000 24.000 24.000 15.000 15.000 23.000
桩号 K716+100.000 K716+100.000 K716+100.000 K716+100.000 K716+100.000 K228+265.899 K718+153.833 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000 K718+210.000
Y 519085.088 519082.168 519082.168 519082.168 518738.184 526279.356 526296.381 526308.590 526294.298 524061.827 526332.070 523920.860 523853.932 523855.632 523825.527 523810.141 523821.966 523803.645 523799.102 523779.297 523778.422 523742.714 523685.632 523563.133 523449.901 523451.714 523436.323 523429.087 523392.676 523399.873 523386.237 523388.033 523367.165 523347.919 523329.614
平曲线的五大要素计算公式

平曲线的五大要素计算公式以下是关于平曲线的五大要素计算公式。
平曲线是指在平面上描述一条曲线的五种基本参数,包括曲线长度、曲线半径、曲线角度、曲线切线和曲线弧度。
下面是这五种要素的计算公式:1.曲线长度(L):曲线长度可以通过计算曲线上的所有坐标点之间的距离来获得。
对于参数方程表示的曲线,曲线长度L可以通过以下公式计算: L=∫(√((dx/dt)²+(dy/dt)²)dt) 其中,(dx/dt)和(dy/dt)分别是曲线在x和y方向上的速度矢量。
2.曲线半径(R):曲线半径表示曲线在某一点处弯曲的程度。
对于圆弧曲线,曲线半径R可以通过以下公式计算: R=(dx²+dy ²)^(1/2)/(1+(dy/dx)²)^(1/2) 其中,(dx,dy)是曲线上的某一点坐标。
3.曲线角度(θ):曲线角度表示曲线在某一点处与x轴的夹角。
对于参数方程表示的曲线,曲线角度θ可以通过以下公式计算: θ=atan2(dy/dx) 其中,(dx,dy)是曲线上的某一点坐标。
4.曲线切线(T):曲线切线表示曲线在某一点处的切线方向。
对于参数方程表示的曲线,曲线切线T可以通过以下公式计算: T=(dx/dt,dy/dt) 其中,(dx/dt)和(dy/dt)分别是曲线在x和y方向上的速度矢量。
5.曲线弧度(α):曲线弧度表示曲线在某一点处沿逆时针方向的旋转程度。
对于圆弧曲线,曲线弧度α可以通过以下公式计算: α=θ 其中,θ是曲线在某一点处与x轴的夹角。
需要注意的是,这些公式适用于平曲线的一般情况。
在实际应用中,根据具体的曲线类型和表示方式,可能需要对公式进行相应的调整。
曲线要素坐标计算
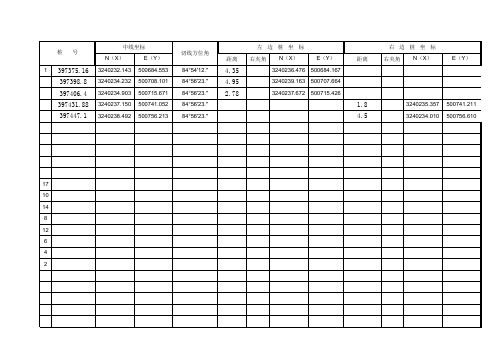
中线坐标
N(X)
E(Y)
切线方位角
距离
左边桩坐标 右夹角 N(X)
E(Y)
距离
右边桩坐标 右夹角 N(X)
E(Y)
1 397375.16 3240232.143 500684.553 84°54′12.″
4.35
3240236.476 500684.167
397398.8 3240234.232 500708.101 84°56′23.″
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号中Leabharlann 坐标切线方位角左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
左边桩坐标
右边桩坐标
桩号
中线坐标
切线方位角
圆曲线坐标计算(坐标正算法)

圆曲线坐标计算(坐标正算法)
单圆曲线是一段具有一定半径的圆弧。 单圆曲线最简单的一种连接两相邻直线的形式。 单圆曲线主要是用于铁路专用线和低等级公路。
一、圆曲线主点
xixZY C co αZs Y i
yiyZY C siαn Z Y i
五、圆曲线测设
1、全站仪坐标放样 将曲线点及控制点坐标数据数据输入全站仪,在控制点上安 置仪器,以相邻控制点为后视点,测设曲线点。 2、检核 在其它控制点上安置仪器,定向后实测各曲线点的坐标,并 与计算值比较,若差值在允许范围内,则测设成果合格,否则说 明测设错误,应查找原因予以纠正。 由于用全站仪极坐标法进行中桩测设时,实际的点位误差主 要是测设时的测量误差,误差一般很小,完全能够达到精度要求, 可不做调整。
通用公式:
XZY i XJDi Ti coαsi1,i YZY i YJDi Ti sinαi1,i
XYZi XJDi Ti coαsi,i1 YYZi YJDi Ti sinαi,i1
Байду номын сангаас
X
起点
ZY1 QZ2 YZ1
JD1
O
JD2
QZ2
ZY2
YZ2
终点
Y
2)计算曲线点坐标
① 计算坐标方位角
i 点为曲线上任意一点。
li 为 i 点与ZY点里程之差。
i
li 180 Rπ
δi
i
2
90li πR
ZY-
i
ZY-
JD
Z Y i Z Y JD i
当曲线左转时用“-”,右转时用“+”。
② 计算弦长
直线 曲线及转角标准计算表(Excel模板).xls
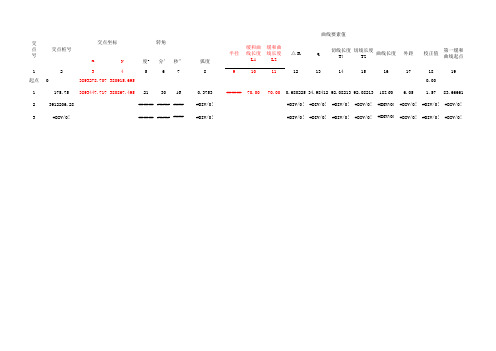
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
曲线
曲线位置
直线长度及方向
第一缓和
第二缓和
曲线终点 或圆曲线
曲线中点
曲线起点 或圆曲线
第二缓和 曲线终点
直线长度 (m)
交点间距 (m)
起点
终点
计算方位角
20
21
22
23
24
14
15
16
17
18
19
0.00
###### 70.00 70.00 0.680225 34.98412 92.08213 92.08213 182.60 6.05 1.57 83.66661
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
2
3912206.28
###### ##### ####
3
#DIV/0!
###### ##### ####
弧度 8
0.3753 #DIV/0! #DIV/0!
曲线要素值
缓和曲 缓和曲
半径 线长度 线长度 △ R
L1
L2
9
10
11
12
q
切线长度 T!
切线长度 T2曲线长度外距来自校正值第一缓和 曲线起点
13
曲线位置直线长度m交点间距m第一缓和曲线终点或圆曲线起点曲线中点第二缓和曲线起点或圆曲线终点直线长度及方向计算方位角第二缓和曲线终点153
交 点 号
1 起点
交点桩号
2 0
交点坐标
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设有缓和曲线的要素计算公式 平曲线要素 缓和曲线长l0 曲线半径R 曲线长Lc 交点前直线切线角A 转向角α 曲线方向判别 内移距p 切垂距m 缓和曲线角β 切线长T 曲线长L 外视距E 切曲差q 交点里程JD ZH点切线方位角 HY点切线方位角 YH点切线方位角 HZ点切线方位角 直缓点ZH里程 缓圆点HY里程 曲中QZ里程 圆缓点YH里程 缓直点HZ里程 缓直点HZ里程
X=XHZ +x*COS(θ 2+π )+y*sin(θ 2+l*π /2) Y=YHZ +x*SIN(θ 2+π )-y*cos(θ 2+l*π /2) θ =θ 1-i*l^2/(2*ls*R) 待求点切线方位角
x=l-l^5/(40*R^2*ls^2)(缓和曲线上) y=l^3/(6*R*ls)-l^7/(336R^3*ls^3)(缓和曲线上)
β 1交点前方位角、β 2 交点后方位角;α 右转 为正,左转为负(弧度制)
l0缓和曲线长(指的是一段的长不是两段的 和) 缓和曲线 缓和曲线(弧度制)
已知
校核无误
注:曲线终点里程必须沿曲线计算,不能沿切线计算。只有把终点里程算出来后,才能接着算下一直线里程; excel表格中角度是弧度制 设有缓和曲线的主要素坐标计算 平曲线要素 方位角θ
0
计算结果 190 1600 1192.29 5.814491681 0.863933132 1 0.940104167 94.98883626 0.059375 833.0276277 1572.293011 162.869954 93.76224494 437703.58 5.814491681 5.873866681 6.619049813 6.678424813 436870.55 437060.55 437656.70 438252.85 438442.85 438442.85
待求点支距坐标x 待求点支距坐标y Ψ
x=q-R*SIN(Ψ) y=p+R*(1-cos(Ψ )) Ψ =(ls/2R)-(l-ls)/R
(圆曲线上) (圆曲线上) (圆曲线上)
交点前直线切线角A 转向角α
度 333 49
分 8 29
秒 45 59
线元切线方位角
度 333
分 8 32 14 38
计算公式
备注 已知(m) 已知(m)
α =β 1-β 2 左=-1,右=1 p=l02/24R m=l0/2-l03/240R2 β 0=l0/2R T=(R+p)*TAN(α /2)+m L=(R*α *π )/180+l0 E=(R+p)sec(α /2)-R q=2T-L JD=ZH+T 333.1458 336.5478 19.2436 22.6456 ZH=JD-T HY=ZH+l0 QZ=HY+L/2-l0 YH=QZ+L/2-l0 HZ=YH+l0 HZ=JD+T-q
秒 45 52 37 44
角度
336 19 22
交点前直线切线角A 方位角θ 1
度 333
分 8
秒 45
方位角θ
2
22
38
44
本曲线段线元要素汇总表
线元切线方位角 计算结果 里程 度 直缓点ZH 缓圆点HY 圆缓点YH 缓直点HZ 436870.55 437060.55 438252.85 438442.85 333 336 19 22 分 8 32 14 38 秒 45 52 37 44 X 857507.217 857678.366 858497.656 858674.394 Y 498827.719 498745.277 498715.174 498784.833 坐标
曲线半径R 转向角α 曲线方向判别 内移距p 前缓和曲线长l1 后缓和曲线长l2 切线长T1 切线长T2 切垂距m 外视距E 切曲差q 曲线长L 交点里程JD 直缓点ZH 缓圆点HY 曲中QZ 圆缓点YH 缓直点HZ ZH(x) ZH(y) HZ(X) HZ(Y) HY(X) HY(Y) θ YH(X) YH(Y) θ 待求点支距坐标x 待求点支距坐标y
1
计算结果 5.814491681
计算公式
备注 交点前导线沿线路前进方向的方位角
方位角θ 交点XБайду номын сангаас 交点Y0
2
0.395239505 858080.92
交点后导线沿线路前进方向的方位角
交点大地坐标
498537.24 1600 5.419252176 1 0.940104167 190 190 643.0499552 643.0499552 94.98883626 -3362.869954 7574.70357 8860.803481 437703.58 437060.53 437250.53 441490.9318 445731.3335 445921.3335 857507.2171 498827.7193 858674.3936 498784.833 857678.3662 498745.2774 T=(R+p)*TAN(α /2)+m T=(R+p)*TAN(α /2)+m m=l0/2-l03/240R2 E=(R+p)sec(α /2)-R q=2T-L L=(R*α *π )/180+l0 JD=ZH+T ZH=JD-T HY=ZH+l0 QZ=HY+L/2-l0 YH=QZ+L/2-l0 HZ=YH+l0 X=X0 +T1*COS(θ 1+π ) Y=Y0 +T1*SIN(θ 1+π ) X=X0 +T1*COS(θ 2) Y=Y0 +T1*SIN(θ 2) X=XZH +x*COS(θ 1)+y*sin(θ 1) Y=YZH +x*SIN(θ 1)-y*cos(θ 1) θ =θ 1+i*l^2/(2*ls*R) 858497.6557 498715.1738 待求点切线方位角 α =θ 1-θ 2 左=-1,右=1 p=l02/24R
