光波的标量衍射理论
合集下载
第三章 标量衍射理论

U ( x, y, z) a exp( jk r )
a exp jk( x cos y cos z cos )
当平面波沿z轴正方向传播时
cos cos 0
U ( z ) a exp( j 2
cos 1
z , 2 ,3 波阵面
2u 1 2u c t
2 2
0
j 2 t
2
2 x
2
2 y
2
2 z 2
u( p, t ) U ( p)e
2 2
c
U ( p) k U ( p) 0
K
2
亥母霍兹方程
三、基尔霍夫积分定理 格林定理 若U(p)和G(p)是两个空间任意复数函数,S为包围体积V 的封闭曲面,U、G在S内和S上它们均单值连续,且一阶 和二阶偏导数单值连续,则有
U ( x, y ) t ( x, y )U ( x, y )
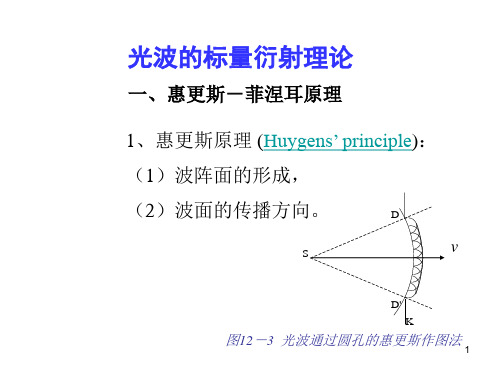
一、惠更斯—菲涅耳原理
1.惠更斯原理:波前上每一个面元都可以看作一个次级 扰动中心,它们产生球面子波,后一时 刻的波前位置是所有这些子波的包络面。
2.惠更斯—菲涅耳原理:波前上任何未受阻挡的点,都 可以看作一个次级波波源,其后空间任 一观察点的光振动是这些子波传播到该 点后叠加的结果。 菲涅耳发展了惠更斯原理,由定性走向了定量计算。
U0为后表面的光场
讨论:当孔用p点的点光源照明时的情况。 推导
r' • P'
n
P0
r • P
经过以上推导,当p近轴,r很大时,180,则有
1 exp( jkr ) 1 cos U ( p) U 0 ( p0 ) r 2 ds j 1 exp( jkr ) 1 cos U 0 ( x0 , y0 ) r 2 dx0dy0 j
信息光学-第3章 标量衍射理论

rz2 x x 0 2 y y 0 2 z1 x x 0 2z 2 y y 0 2
对上式进行二项式展开,并考虑徬轴近似,上式可进一步简化为:
rzxx02yy02
泰勒公式:f(x)=f(a) + f'(a)(x-a)/1! + f''(a2整)z理(xpp-ta)^2/2! + …… + f(n)(a)(x-a)^n/n!
此时,称A(cos/,cos/ )为xy平面上复振幅分布的角谱。 引入角谱概念有助于进一步理解复振幅分解的物理意义: (1)单色光波场中某一平面上的场分布可看作不同方向传播的
单色平面波的叠加; (2) 在叠加时各平面波成分有自己的振幅和常量相位,它们
的值分别取决于角谱的模和幅角。
角谱如何求?就用傅里叶变换整理就ppt 行,注意坐标替换
整理ppt
试写出传播方向余弦为(cosα,0)的单色平面波在x-y平 面上的复振幅分布(用空间频率来描述)
(fxcos/, fy0)
U (x ,y )A ex p (j2 fxx )
整理ppt
k kx kz;
朝X正方向, fx cos/;
2)不能,波长应该是不会变长的
3)波长应该由时间域的频率 f 决定,即波形变 化的快慢,不是由空间频率决定的。波长=c/f。 也可由公式:X=波长/cosa得到。
1、光波的数学描述
将简化式代入球面波复振幅表达式有:
UP a0 ejkr
r
rzxx02yy02
2z
思考,公式中的近似 条件为何位相里面不 考虑成r=z
jk z x x02 y y02
U P ae aee 0
2z
0 jkz j2 k z x x02 y y02
对上式进行二项式展开,并考虑徬轴近似,上式可进一步简化为:
rzxx02yy02
泰勒公式:f(x)=f(a) + f'(a)(x-a)/1! + f''(a2整)z理(xpp-ta)^2/2! + …… + f(n)(a)(x-a)^n/n!
此时,称A(cos/,cos/ )为xy平面上复振幅分布的角谱。 引入角谱概念有助于进一步理解复振幅分解的物理意义: (1)单色光波场中某一平面上的场分布可看作不同方向传播的
单色平面波的叠加; (2) 在叠加时各平面波成分有自己的振幅和常量相位,它们
的值分别取决于角谱的模和幅角。
角谱如何求?就用傅里叶变换整理就ppt 行,注意坐标替换
整理ppt
试写出传播方向余弦为(cosα,0)的单色平面波在x-y平 面上的复振幅分布(用空间频率来描述)
(fxcos/, fy0)
U (x ,y )A ex p (j2 fxx )
整理ppt
k kx kz;
朝X正方向, fx cos/;
2)不能,波长应该是不会变长的
3)波长应该由时间域的频率 f 决定,即波形变 化的快慢,不是由空间频率决定的。波长=c/f。 也可由公式:X=波长/cosa得到。
1、光波的数学描述
将简化式代入球面波复振幅表达式有:
UP a0 ejkr
r
rzxx02yy02
2z
思考,公式中的近似 条件为何位相里面不 考虑成r=z
jk z x x02 y y02
U P ae aee 0
2z
0 jkz j2 k z x x02 y y02
3.1光波的标量衍射理论-邓冬梅

2
2
z12
= z1
( x x1 ) + ( y y1 ) +
2
2
2 z1
[( x x1 ) + ( y y1 ) ]2 + .... 3 8 z1
2 2
r ≈ z1
(x x1 )2 + ( y y1 )2 +
2 z1
C
y1 x1 Q z1 K r
y P x
近似条件: [( x x1 ) + ( y y1 ) ] z >> 4λ
一,光的衍射现象
'光线'拐弯了! 光线'拐弯了! 光线
S
?
衍射现象:光波偏离直线传播而出 衍射现象: 现光强不均匀分布的现象
E
E
S
S
圆孔衍射
Diffraction pattern of an icosahedral quasicrystal
12
光孔尺寸与衍射
衍射效应很弱,光线几乎直线传播 直线传播. 一,ρ>1000λ时,衍射效应很弱,光线几乎直线传播. λ 但在影界边缘,衍射现象仍不可忽略. 但在影界边缘,衍射现象仍不可忽略. 二,1000λ >ρ> λ时,衍射现象显著,出现了与光孔 衍射现象显著 现象显著, λ ρ 形状对应的衍射图样. 形状对应的衍射图样. 衍射效应过于强烈,只看到干涉 干涉. 三,ρ ~ λ 衍射效应过于强烈,只看到干涉. 过渡. 四,ρ<λ 向散射过渡. λ 散射过渡 其中:光孔线度ρ,波长λ
π
( n,l ) ( n,r ) ∑
θ
l
r P
K一般在0-1之间,特别地, 光线正入射时:
R
2
z12
= z1
( x x1 ) + ( y y1 ) +
2
2
2 z1
[( x x1 ) + ( y y1 ) ]2 + .... 3 8 z1
2 2
r ≈ z1
(x x1 )2 + ( y y1 )2 +
2 z1
C
y1 x1 Q z1 K r
y P x
近似条件: [( x x1 ) + ( y y1 ) ] z >> 4λ
一,光的衍射现象
'光线'拐弯了! 光线'拐弯了! 光线
S
?
衍射现象:光波偏离直线传播而出 衍射现象: 现光强不均匀分布的现象
E
E
S
S
圆孔衍射
Diffraction pattern of an icosahedral quasicrystal
12
光孔尺寸与衍射
衍射效应很弱,光线几乎直线传播 直线传播. 一,ρ>1000λ时,衍射效应很弱,光线几乎直线传播. λ 但在影界边缘,衍射现象仍不可忽略. 但在影界边缘,衍射现象仍不可忽略. 二,1000λ >ρ> λ时,衍射现象显著,出现了与光孔 衍射现象显著 现象显著, λ ρ 形状对应的衍射图样. 形状对应的衍射图样. 衍射效应过于强烈,只看到干涉 干涉. 三,ρ ~ λ 衍射效应过于强烈,只看到干涉. 过渡. 四,ρ<λ 向散射过渡. λ 散射过渡 其中:光孔线度ρ,波长λ
π
( n,l ) ( n,r ) ∑
θ
l
r P
K一般在0-1之间,特别地, 光线正入射时:
R
第二章 光的标量衍射理论

(2-1-15)
(2-1-15)式称为菲涅尔衍射积分公式 式称为菲涅尔衍射积分公式 满足菲涅耳近似条件的衍射称为菲涅耳衍射 满足菲涅耳近似条件的观察区域称为“菲涅尔衍射区” 满足菲涅耳近似条件的观察区域称为“菲涅尔衍射区” 在菲涅耳衍射区中放置一个二维观察屏, 在菲涅耳衍射区中放置一个二维观察屏,屏上显示的图 形即物体的菲涅耳衍射图形。 形即物体的菲涅耳衍射图形。 辐照度L(x,y) 为: 辐照度
• 2.1.1 惠更斯 菲涅耳原理 惠更斯-菲涅耳原理 • 假设:波前上的每一个面元都可以看做是一个次级扰 假设: 动中心,它们能产生球面子波. 动中心,它们能产生球面子波.后一时刻的波前位置 是所有这些子波波前的包络面。 是所有这些子波波前的包络面。 波前”即是某一时刻光波的波面(等相面 等相面), “波前”即是某一时刻光波的波面 等相面 , 次级扰动中心” 是一个点光源或称为子波源。 “次级扰动中心” 是一个点光源或称为子波源。
该近似称为夫琅和费近似 该近似下 基尔霍夫衍射积分公式化简为: 在该近似下,基尔霍夫衍射积分公式化简为:
x2 + y2 E ( x, y ) = exp j k d + jλ d 2d 1 ∞ k ∫ ∫ A(ξ ,η ) exp − j ( xξ + yη ) d ξ d η d −∞ (2-1-19) )
(2-1-16) )
L(x,y)等于菲涅耳衍射复振幅分布 等于菲涅耳衍射复振幅分布E(x,y)的模的平方 等于菲涅耳衍射复振幅分布 的模的平方
二、夫琅和费近似和天琅和费衍射
进一步增大观察平面∏到衍射孔径 的距离 进一步增大观察平面 到衍射孔径∑的距离 ,则衍射 到衍射孔径 的距离d, 图形将随之放大。 图形将随之放大。
第2章 标量衍射理论

一级近似 二级近似
对振幅中r 的可作一级近似. 但因为 k 很大, 对位相中的 r 须作二级近似
§2.1 光波的数学描述
球面波 : 近轴近似
a0 k 2 2 U ( P) U ( x, y) exp( jkz) exp j ( x x0 ) ( y y0 ) z 2z
本章将从基尔霍夫衍射理论和角谱出发,讨论衍射问题。前者
与经典物理光学的陈述一致,但利用线性系统理论赋予了新的 解释。我们将把衍射这一物理现象看做线性不变系统,分别讨 论其脉冲响应和传递函数。重点放在角谱理论上。
第2章 标量衍射理论(Theory of Scalar Diffraction)
§2.1 光波的数学描述 2.1.1 单色光波场的复振幅表示
p
l
l
z l fx l f y )
在任一距离z的平面上的复振幅分布,由在 z =0平面上的复 振幅和与传播距离及方向有关的一个复指数函数的乘积给出。 这说明了传播过程对复振幅分布的影响,已经在实质上解决 了最基础的平面波衍射问题
普遍的光振动的复振幅表达式: U(P) = a(P) e jj(P) 光强分布: I = UU*
U ( x, y) A exp[jk ( x cosa y cos b )]
§2-2 基尔霍夫衍射理论
2.2.1 从惠更斯-菲涅耳原理到基尔霍夫衍射公式
衍射理论要解决的问题是:光场中任意一点为P 的复 振幅 U(P) 能否用光场中其它各点的复振幅表示出来。
1. 惠更斯包络作图法 (1678): 从某一时刻的波阵面求下一 时刻波阵面的方法。把波阵面上每一面元作为次级子波 的中心,后一时刻的波阵面是所有这些子波的包络面。
对振幅中r 的可作一级近似. 但因为 k 很大, 对位相中的 r 须作二级近似
§2.1 光波的数学描述
球面波 : 近轴近似
a0 k 2 2 U ( P) U ( x, y) exp( jkz) exp j ( x x0 ) ( y y0 ) z 2z
本章将从基尔霍夫衍射理论和角谱出发,讨论衍射问题。前者
与经典物理光学的陈述一致,但利用线性系统理论赋予了新的 解释。我们将把衍射这一物理现象看做线性不变系统,分别讨 论其脉冲响应和传递函数。重点放在角谱理论上。
第2章 标量衍射理论(Theory of Scalar Diffraction)
§2.1 光波的数学描述 2.1.1 单色光波场的复振幅表示
p
l
l
z l fx l f y )
在任一距离z的平面上的复振幅分布,由在 z =0平面上的复 振幅和与传播距离及方向有关的一个复指数函数的乘积给出。 这说明了传播过程对复振幅分布的影响,已经在实质上解决 了最基础的平面波衍射问题
普遍的光振动的复振幅表达式: U(P) = a(P) e jj(P) 光强分布: I = UU*
U ( x, y) A exp[jk ( x cosa y cos b )]
§2-2 基尔霍夫衍射理论
2.2.1 从惠更斯-菲涅耳原理到基尔霍夫衍射公式
衍射理论要解决的问题是:光场中任意一点为P 的复 振幅 U(P) 能否用光场中其它各点的复振幅表示出来。
1. 惠更斯包络作图法 (1678): 从某一时刻的波阵面求下一 时刻波阵面的方法。把波阵面上每一面元作为次级子波 的中心,后一时刻的波阵面是所有这些子波的包络面。
标量衍射理论

x0 2
y
y0 2
z 1
1 2
x x0 z
2
1 2
y y0 z
2
可以进一步简化得出:
r z x2 y2 xx0 yy0
2z
z
这一近似称为夫琅禾费近似或远场近似,在这一条 件下,脉冲响应可进一步简化为:
h(x0 ,
y0 ;
x,
y)
exp( jkz)
jz
exp
j
k 2z
y
y0 2
z
1
x x0 z
2
y y0 z
2 2
当
cos(n, r) 1时
x
z
x0
2
和
y
y0
2
都是小量
z
r
z
1
x
x0
2
2z
2
y
y0 2
x x0 2 y
8z4
y0 2
2
r
z2
x x0 2
y
y0 2
z 1
1 2
x x0 z
2
1 2
§2.2 从矢量理论到标量理论 光的电磁理论
介质中无自由电荷
麦
E 0
克 斯
H 0
韦 方 程
E H
t
组
H E
t
符号: E 电场强度
直角坐标系分量 (Ex , Ey , Ez )
H 磁场强度
直角坐标系分量 (H x , H y , H z )
E, H 都是位置(x,y,z)和时间 t 的函数
cos(n,
r
)
- cos(n, 2
r0
光波的标量衍射理论
~
E
P=
A i
e
xpik
l
l
e
xpik
r
r
cosn,
r
2
cosn,
l
d
子波的复振幅与
K() cosn, r cosn,l
2 成正比,与波长成反比。
i 1 exp[i p]
i
2
表示子波的振动位相超前于入射波90。
6
当光线接近于正入射时 exp(ikl) exp(ikR)
l
R
cos(n, l) 1,
1 x x1 2 y y1 2
z12
z1
x
x1 2 y
2z1
y1 2
[x
x1 2 y
8z13
y1 2 ]2 ....
级数展开
r
z1
x
x1
2 y
2z1
y1 2
近似条件:
[x x1 2 y y1 2 ]2 p
z13
4
y1
Q C
K
x1 r
z1
y x
P
P0 E
11
r
z1
x
x1 2 y
2
光源S在波面ZZ '上
波阵面外任一点光振动应该是波面
上所有子波相干叠加的结果。
任意Q点产生的复振幅:
E~Q
A
exp ikR
R
Z
Q
R
Q点处d 大小的面元
r P
对P点的贡献为: S
dE~P
CK
E~Q
expik
r
r
d
Z'
子波向P点的球面波公式 子波法线方向的振幅 子波振幅随角的变化
第二章 光的标量衍射理论

4.若/a趋于零衍射现象消失—几何光学是/a趋于零 的极限情况
2.1.1.2.衍射屏和衍射系统 障碍物—衍射屏
照明 空间
x0 , y0
衍射 空间
x, y
U 0 U0
U0是衍射屏前表面的复振幅
是衍射屏后表面的复振幅 U0
照明 空间
U0 U0
衍射屏
t
U x, y
(2.2.1)
.
y
.
0
复振幅分布U(x,y可分解为频率不同的复指数分 量的线性组合,各频率分量的权重因子为A(fx,fy)
z
A( f x , f y )
exp[ j 2 ( f x x f y y)] 代表一个沿 cos f x ,cos f y 所确定方向传播的单色振幅平面波。
复振幅透射函数—屏函数 图2.1.1 衍射系统及其三个重要的分析平面 ( x0 , y0 ) U0 t ( x0 , y0 ) U 0 ( x0 , y0 ) --瞳函数 振幅型—只改变振幅 位相型—只改变位相 ( x0 , y0 ) t ( x0 , y0 )U 0 ( x0 , y0 ) 或 U0
exp( jkr ) dU ( P) CU ( P0 )dSK ( ) r
dS
U ( P0 )
n
P0
r
Σ
图2.1.2
U (P)
波面Σ 在P点的复振幅 (2.1.3)
P
Σ 上所有子波源在P点产生的总振动为
U ( P) C U ( P0 ) K ( )
exp( jkr ) dS r
y
3D
k与x轴夹角为 , 与y轴夹角为,与z轴夹角为
x
2.1.1.2.衍射屏和衍射系统 障碍物—衍射屏
照明 空间
x0 , y0
衍射 空间
x, y
U 0 U0
U0是衍射屏前表面的复振幅
是衍射屏后表面的复振幅 U0
照明 空间
U0 U0
衍射屏
t
U x, y
(2.2.1)
.
y
.
0
复振幅分布U(x,y可分解为频率不同的复指数分 量的线性组合,各频率分量的权重因子为A(fx,fy)
z
A( f x , f y )
exp[ j 2 ( f x x f y y)] 代表一个沿 cos f x ,cos f y 所确定方向传播的单色振幅平面波。
复振幅透射函数—屏函数 图2.1.1 衍射系统及其三个重要的分析平面 ( x0 , y0 ) U0 t ( x0 , y0 ) U 0 ( x0 , y0 ) --瞳函数 振幅型—只改变振幅 位相型—只改变位相 ( x0 , y0 ) t ( x0 , y0 )U 0 ( x0 , y0 ) 或 U0
exp( jkr ) dU ( P) CU ( P0 )dSK ( ) r
dS
U ( P0 )
n
P0
r
Σ
图2.1.2
U (P)
波面Σ 在P点的复振幅 (2.1.3)
P
Σ 上所有子波源在P点产生的总振动为
U ( P) C U ( P0 ) K ( )
exp( jkr ) dS r
y
3D
k与x轴夹角为 , 与y轴夹角为,与z轴夹角为
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
是不正确的。
三、 基尔霍夫衍射公式的近似
1) 傍轴近似
对于傍轴光线,如图所示衍射屏的开孔Σ的线度和接受
屏上的考察范围都远小于衍射屏到接受屏的距离。
Σ 的线度<< z1 P0P 的线度<< z1
① cos(n z1。
y1
x1 r Q
C
z1
K
y Px P0
E
③倾斜因子 K() 表示了次波的振幅在各个方向上是不同
的,其值在 0 与 1 之间。
如果一平行光垂直入射到Σ 上,则 cos(n, l) =-1,cos(n,
r)= cos,
K( ) 1 cos
2
当=0 时,K() =1,这表明在入射波面法线方向上
的次波贡献最大;当= 时,K()=0。这一结论说
明,菲涅耳在关于次波贡献的研究中假设 K(/2)=0
球面波
平面波
vt
传 播 方
...
.
.
传
向
. 波源 .
.
播 方
vt . . .
.
向
.
t 波面
t 波面
t + t 波面
t
t + t 波面
用惠更斯原理证明折射定律
i
B
Ai
n1
rD
C
r
n2
菲涅尔基于光的干涉原理,用“子波相干叠加”思想补 充了惠更斯原理:波前(波面)上的每一点都可以看作 为一个发出球面子波的次级扰动中心,在其后面一个时 刻波面上任意一点的光振动就是这些子波在该点相干叠 加的结果——定量地说明了衍射现象。
e 2 z1
i z1
E%( x1
,
y1
)e
ik
xx1
yy1 z1
dx1dy1
(14)
菲涅耳衍射和夫朗和费衍射是傍轴近似下的两种衍射 情况,二者的区别条件是观察屏到衍射屏的距离 z1 与 衍射孔的线度(x1,y1)之间的相对大小。
惠更斯—菲涅耳原理的图像表示
z
n
R Qr
P点光场分布可以看作是 S 和 P S
P
之间任一波面Σ(通过孔径zz’的
部分)上各点发出的次波在 P 点 z
相干叠加的结果。
任意一点Q发出的子波满足以下假设:
1、Q点处发出的子波在P点的振幅正比于子波的面积ds,
并且随着倾斜角θ 的增大而减小。
2、因为波面Σ是一个等相位面,所以没一点上发出的子
M
K1
K2
K3
K4
几何投影区 菲涅耳衍射区
夫朗和费衍射区
(1) 菲涅耳近似
如图所示,设 QP r,则由几何关系有
r
z12 (x x1)2 ( y y1)2 z1
1
x
x1 z1
2
y
y1 z1
2
z1 1
1 2
(x
x1 ) 2
(y z12
y1 ) 2
1 8
(x
E%(P) 1
i
Aeikl l
eikr r
cos(n,
r
)
2
cos(n,
l)
d
(7)
(n, r) (n, l)
C
1
i
;
K
(
)
cos(n,
r
)
2
cos(n,
l
)
n S
l
Q r
P
此式称为菲涅耳—基尔霍夫衍射公式。
① P 点的光场是孔径所限波面Σ 上无穷多次波源产生的
② 因子(- i) 表明,次波源的振动相位超前于入射波 /2
一、惠更斯—菲涅耳原理
1690年惠更斯提出的一种假设:波前(波面)上的每 一点都可以看作为一个发出球面子波的次级扰动中心, 在其后面一个时刻,这些子波的包络面就是新的波 前——定性地说明了衍射现象
原理的依据: 1、波动在介质中是逐点传播的 2、各质点作与波源完全相同的振动
注意:该原理对非均匀媒质也成立,只是波前的形状 和传播方向可能发生变化。
k (x12 y12 )max <<π (12) 2z1
可将 r 进一步简化为
r
z1
x2 y2 2z1
xx1
z1
yy1
(13)
这一近似称为夫朗和费近似,在这个区域内观察到的 衍射现象叫夫朗和费衍射(远场衍射)。
在夫朗和费近似下,P 点的光场复振幅为
E%(x, y)
eikz1
ik x2 y2
波的初相位相同
3、子波在P引起的振幅与r成反比4、某一点发出的子波
在P点的相位有光程决定 z
R Qr
S
P
z
z
RQ r
S
P 点的光场复振幅为
P E%(P)= C A eikR eikr K ( )d L (5) R r
z
A 是离点光源S单位距离处的振幅;R是波面Σ的半径
C 是比例系数, r Q,P K() 称为倾斜因子,它是与元 波面 法d线和 的夹QP角 (称为衍射角)有关的量
菲涅耳的假设:当=0 时,K 有最大值;随着 的增大,K 迅速减小,当 ≥/2 时,K=0。
从惠更斯——菲涅尔原理我们可以看出,光的衍射 现象实质上还是一个干涉问题:相干光波叠加引起 的光强的重新分布,所不同之处在于:
(1)干涉现象是有限个相干光波的叠加的结果
(2)衍射现象则是无限多个相干光波的叠加的结果。
x1 ) 2
(y z12
y1 ) 2
2
L
y1
x1 r Q
C
z1
y
Px
P0
k [(x x1)2 8
(y z13
y1
)2
]2 max
π
(9)
K
r简化为
r
z1
1
1 2
(x
x1 ) 2
( z12
y
y1 ) 2
z1
x2 y2 2 z1
xx1
z1
yy1
x12 y12 2 z1
(10)
这一近似称为菲涅耳近似,在这个区域内观察到的衍
射现象叫菲涅耳衍射(近场衍射)。
在菲涅耳近似下,P 点的光场复振幅为
E%(x, y) 1
i z 1
E%( x1 ,
ikz1[1
y1)e
(
x x1
)2 ( y 2 z12
y1
)2
]
dx1dy1
(11)
(2) 弗朗和费近似 当观察屏离孔的距离很大,菲涅尔近似公式中,满足
E%(P)=C A eikR eikr K ( )d R r
(5)
菲涅尔发展的理论确实能够定性地解释某些衍 射现象,但是从理论上讲它本身是不严格的, 主要有以下几点:
(1)倾斜因子的引入缺乏理论根据;
(2)倾斜因子的具体表达式未知;
(3)常数项的具体形式未知
基尔霍夫从微分波动方程出发,利用格林定理,以及电 磁场的边值条件给出了惠更斯—菲涅耳原理较完善的 数学表达式,确定了倾斜因子和常数项的表达式,弥 补了菲涅尔理论的不足。
所以衍射公式改写为
E%(P) 1 E%(Q)eikrd L (8)
i z1
2) 距离近似—菲涅耳近似和夫朗和费近似
①在离圆孔很近的 K1 处,是圆孔的几何投影区 ②在 K2 面的前后,随着观察平面距离的增大,环纹中 心表现出亮暗交替变化现象。——菲涅尔衍射区
③在 K4 位置,随着观察距离的增大,只是光斑扩大, 但光斑形状不变。——弗朗和费衍射区
