最小二乘定位解算matlab代码
最小二乘法--计算方法
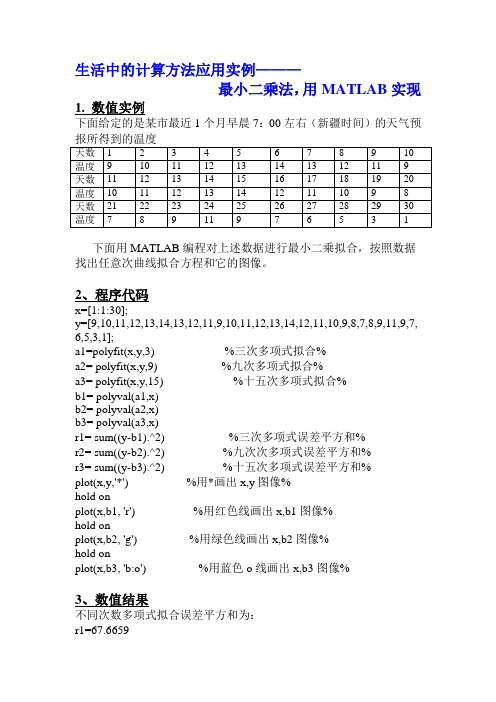
生活中的计算方法应用实例———最小二乘法,用MATLAB实现1. 数值实例下面给定的是某市最近1个月早晨7:00左右(新疆时间)的天气预报所得到的温度天数 1 2 3 4 5 6 7 8 9 10 温度9 10 11 12 13 14 13 12 11 9 天数11 12 13 14 15 16 17 18 19 20 温度10 11 12 13 14 12 11 10 9 8 天数21 22 23 24 25 26 27 28 29 30 温度7 8 9 11 9 7 6 5 3 1下面用MATLAB编程对上述数据进行最小二乘拟合,按照数据找出任意次曲线拟合方程和它的图像。
2、程序代码x=[1:1:30];y=[9,10,11,12,13,14,13,12,11,9,10,11,12,13,14,12,11,10,9,8,7,8,9,11,9,7, 6,5,3,1];a1=polyfit(x,y,3) %三次多项式拟合%a2= polyfit(x,y,9) %九次多项式拟合%a3= polyfit(x,y,15) %十五次多项式拟合%b1= polyval(a1,x)b2= polyval(a2,x)b3= polyval(a3,x)r1= sum((y-b1).^2) %三次多项式误差平方和%r2= sum((y-b2).^2) %九次次多项式误差平方和%r3= sum((y-b3).^2) %十五次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%hold onplot(x,b2, 'g') %用绿色线画出x,b2图像%hold onplot(x,b3, 'b:o') %用蓝色o线画出x,b3图像%3、数值结果不同次数多项式拟合误差平方和为:r1=67.6659r2=20.1060r3=3.7952r1、r2、r3分别表示三次、九次、十五次多项式误差平方和。
用matlab中最小二乘法编程求解

个人收集整理-ZQ
解:拟合两组数据、,已知,只需确定多项式系数、、.根据最小二乘原则,使所求问题成为三元一次函数()地极小点问题.
由多元函数取极值地必要条件知比为
,,
地解,即满足
将三元一次线性方程组带入,其程序如下:
>> [,...资料个人收集整理,勿做商业用途
];资料个人收集整理,勿做商业用途
[,...资料个人收集整理,勿做商业用途
,...资料个人收集整理,勿做商业用途
];
>> (*.^)(*.^)(*.^)(*.^)(*.^)(*.*)(*.^.*)(*.^.*)资料个人收集整理,勿做商业用途
>> []('***','***','*** ','');资料个人收集整理,勿做商业用途
>> ()()()
1 / 1。
matlab function编程最小二乘法

matlab function编程最小二乘法在MATLAB中,使用最小二乘法拟合数据通常涉及到使用函数进行编程。
以下是一个简单的MATLAB函数,用于实现最小二乘法拟合直线的例子:function [coefficients, fittedData] = leastSquaresFit(x, y, degree)% x: 输入数据的 x 值% y: 输入数据的 y 值% degree: 拟合多项式的次数% 创建 Vandermonde 矩阵A = zeros(length(x), degree + 1);for i = 1:degree + 1A(:, i) = x.^(degree + 1 - i);end% 使用最小二乘法计算系数coefficients = (A' * A)\(A' * y);% 生成拟合曲线的数据fittedData = polyval(coefficients, x);% 绘制原始数据和拟合曲线figure;plot(x, y, 'o', x, fittedData, '-');legend('原始数据', '拟合曲线');xlabel('X轴');ylabel('Y轴');title('最小二乘法拟合');end你可以通过调用这个函数并提供你的数据和拟合多项式的次数来进行最小二乘法拟合。
例如:x = [1, 2, 3, 4, 5];y = [2.1, 2.8, 3.4, 3.7, 4.2];degree = 1;[coefficients, fittedData] = leastSquaresFit(x, y, degree);disp('拟合系数:');disp(coefficients);这是一个简单的线性拟合的例子。
你可以根据需要修改该函数,以适应高次多项式的情况。
matlab最小二乘解方程

matlab最小二乘解方程最小二乘法是求解线性方程组的一种有效方法,可以通过最小化误差平方和来得到最优解。
在MATLAB中,我们可以使用“\”操作符或者使用“pinv”函数来求解一个线性方程组的最小二乘解。
以下是关于如何在MATLAB中使用最小二乘法来求解线性方程组的详细内容:1. 使用“\”操作符使用“\”操作符可以很方便地求解一个线性方程组的最小二乘解。
例如,假设我们有一个由n个方程组成的线性方程组:Ax = b其中,A是一个m ×n的矩阵,x是一个n维向量,b是一个m维向量。
则它的最小二乘解为:x = (A' A)^(-1) A' b在MATLAB中,我们可以通过以下代码实现最小二乘解:A = [1 1 1; 2 3 4; 4 5 7; 5 6 8];b = [1; 2; 3; 4];x = A \ b;其中,反斜杠符号“\”表示求解线性方程组的最小二乘解。
2. 使用“pinv”函数除了使用“\”操作符,我们也可以使用MATLAB中的“pinv”函数来求解一个线性方程组的最小二乘解。
例如,我们可以通过以下代码实现最小二乘解:A = [1 1 1; 2 3 4; 4 5 7; 5 6 8];b = [1; 2; 3; 4];x = pinv(A) * b;其中,pinv函数表示求矩阵A的伪逆矩阵。
使用“pinv”函数来求解线性方程组的最小二乘解与使用“\”操作符的结果是等价的。
需要注意的是,在使用最小二乘法来求解线性方程组时,矩阵A的列应该是线性无关的,否则可能会出现唯一最小二乘解不存在的情况。
综上所述,MATLAB中使用最小二乘法来求解线性方程组非常简单。
我们可以通过“\”操作符或者“pinv”函数来求解一个线性方程组的最小二乘解。
#matlab用于最小2乘法计算实例

计算法(最小二乘法):2组数据:x 1, x 2, x 3….. x n 为测量数据列,比如半导体电阻的温度y 1, y 2, y 3….. y n 为测量数据列,比如半导体电阻的端电压计算相关系数e R X Y XY ⋅-=, 如|Re |很接近1,则x 和y 是线性关系。
可用y =a x +b 表示 22X Y X Xa Y X ⋅-=- , b a Y X =- 其中: 1()/n i i X x n ==∑ ; 122()/n i i x X n ==∑ ; 1()/n i i Y y n ==∑ ; 122()/ni i y Y n ==∑ ; 1()/ni i i XY x y n ==∑ 计算Re ,a ,b 的matlab 语句:Re =(mean(x.*y)-(mean(x))* (mean(y)))/sqrt((mean(x.*x)-(mean(x))^2)*( (mean(y.*y)-(mean(y))^2)))a =(mean(x.*y)-(mean(x))* (mean(y)))/ ((mean(x.*x)-(mean(x))^2))b =mean(y)-a *mean(x)例如,对于半导体热敏特性实验:%本实验中用的半导体热敏电阻,它的阻值与温度关系近似满足011()0B T T R R e -=式中R 0为T 0 时的电阻(初值), R 是温度为T 时的电阻,B 为温度系数(热敏指数)。
B 在工作温度范围内并不是一个严格的常数,但在我们的测量范围内,它的变化不大。
%将上式变形得到: 1ln R B C T=⋅+ 以ln R 为纵轴,1/T 为横轴做图,直线的斜率即为B 值。
%亦可以用计算法(最小二乘法)求出B 和C,matlab 计算如下:t=[10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30] %输入热敏电阻的温度数据(摄氏T=273.17+t %换算为热力学温度u=[110,108,103,97,93,89,84,80,76,72,69,65,62,59,56,54,51,49,47,45,43] %输入热敏电阻二端的电压数据(m R=u.*50%计算热敏电阻的阻值,实验中通过热敏电阻的电流为20uAx=1./T %lnR=B/T+C , 作变量代换:令y= lnR ,x=1/Ty=log(R) %matlab中log表示自然对数lnRe=(mean(x.*y)-(mean(x))* (mean(y)))/sqrt((mean(x.*x)-(mean(x))^2)*( (mean(y.*y)-(mean(y))^2)))B=(mean(x.*y)-(mean(x))* (mean(y)))/ ((mean(x.*x)-(mean(x))^2))C=mean(y)-B*mean(x)%输入自己的温度t,电压u数据组,复制到matlab命令窗口,就可得结果。
最小二乘算法matlab代码实现

最小二乘算法matlab代码实现最小二乘算法是一种常用的线性回归方法,它可以用来拟合数据,预测未来趋势。
在matlab中,我们可以使用内置函数来实现最小二乘算法。
首先,我们需要准备一些数据。
假设我们有一组数据,包含x和y两个变量,我们希望通过这组数据来拟合一条直线。
```matlabx = [1, 2, 3, 4, 5];y = [2.1, 3.9, 6.2, 8.1, 10.1];```接下来,我们可以使用polyfit函数来拟合一条一次函数,该函数返回的是拟合直线的系数。
```matlabp = polyfit(x, y, 1);```其中,第一个参数是自变量,第二个参数是因变量,第三个参数是拟合的次数。
在本例中,我们拟合的是一次函数,所以拟合的次数为1。
接着,我们可以使用polyval函数来计算拟合直线的值。
```matlabyfit = polyval(p, x);```最后,我们可以绘制原始数据和拟合直线的图像。
```matlabplot(x, y, 'o', x, yfit, '-')legend('原始数据', '拟合直线')```完整的matlab代码如下:```matlabx = [1, 2, 3, 4, 5];y = [2.1, 3.9, 6.2, 8.1, 10.1];p = polyfit(x, y, 1);yfit = polyval(p, x);plot(x, y, 'o', x, yfit, '-')legend('原始数据', '拟合直线')```通过以上代码,我们可以实现最小二乘算法的拟合过程,并得到拟合直线的系数和图像。
加权递归最小二乘 matlab代码

加权递归最小二乘 matlab代码以下是使用Matlab编写的加权递归最小二乘法的示例代码:matlab复制代码function [theta, P] = wrrs(X, Y, theta, P, la mbda) % WRRSLS 加权递归最小二乘法 % X, Y 是观测数据矩阵,theta 是初始参数向量,P 是初始协方差矩阵,lambda 是正则化参数 % 返回 theta 和 P % 计算权值% WRRSLS 加权递归最小二乘法 % X, Y 是观测数据矩阵,theta 是初始参数向量,P 是初始协方差矩阵,l ambda 是正则化参数 % 返回 theta 和 P % 计算权值 N = length(X); Xb = (X'*P*X + lambda*eye(size(X,1))).^(-1)*X'; W = (P*X'*X*P + lambda*eye(size(P,1))).^(-1); % 计算参数向量和协方差矩阵 theta = Xb*Y; P = (eye(size(P)) - Xb*X)*P; % 计算误差向量和残差矩阵 e = Y - X*theta; R = (X*P*X') + lambda*eye(size(X)); % 计算加权残差向量和加权残差矩阵 eW = W*e; RW = R*W; % 计算加权递归最小二乘法的参数向量和协方差矩阵 theta = theta + eW'; P = RW*P*RW'; end该函数接受观测数据矩阵X、观测数据向量Y、初始参数向量theta、初始协方差矩阵P 和正则化参数lambda 作为输入,并返回最终的参数向量thet a 和协方差矩阵P。
在函数内部,首先计算权值W,然后使用加权最小二乘法计算参数向量theta 和协方差矩阵P,最后计算误差向量和残差矩阵,以及加权残差向量和加权残差矩阵,并使用它们更新参数向量和协方差矩阵。
matlab 最小二乘法

在Matlab中,可以使用“\”或者pinv函数进行最小二乘法的求解。
下面给出一个使用“\”运算符进行最小二乘法的例子:
假设有一个线性方程组Ax = b,其中$A$ 是m×n的矩阵,x是n×1的未知向量,b 是m×1的已知向量,且m>n。
最小二乘法的目标是找到一个x,使得Ax≈b,即∥Ax−b∥最小。
使用Matlab中的“\”运算符求解最小二乘法的代码如下:
% 生成数据
x = [0:0.1:1]';
y = 2*x + randn(size(x))*0.1;
% 构造矩阵A和向量b
A = [x, ones(size(x))];
b = y;
% 求解最小二乘问题
x_ls = A \ b;
% 输出结果
fprintf('斜率:%f,截距:%f\n', x_ls(1), x_ls(2));
在这个例子中,我们生成了一个带噪声的数据集,然后构造了矩阵A 和向量b,其中A的第一列为x,第二列为常数项1。
最后,使用“\”运算符求解最小二乘问题,并输出斜率和截距的值。
需要注意的是,在实际应用中,最小二乘法的精度和稳定性可能会受到多种因素的影响,如数据噪声、矩阵奇异性等等。
因此,在使用最小二乘法时需要对数据和算法进行充分的分析和优化,以保证结果的准确性和可靠性。
