逻辑代数及其化简
合集下载
逻辑代数基本原理及公式化简
2.1.3 逻辑代数的基本规则
4、附加公式
附加公式二： 一个包含有变量x、x 的函数f，可展开为 x·f和
x·f的逻辑或。 一个包含有变量x、x 的函数f，可展开为（x+f）和
（x+f）的逻辑与。
利用附加公式一，可以改写为：
2.1.3 逻辑代数的基本规则
4、附加公式
例题：化简函数 AB BD （A B）(A B)(B E)
2.1.2 逻辑代数的基本公式
基本公式验证方法： 真值表 利用基本定理化简公式 例：真值表验证摩根定律
A B A B A＋B A＋B A B 00 1 1 1 1 01 1 1 0 0 10 1 1 0 0 11 0 0 0 0
A______•____B______
__ __
A B
__ __
A B A • B
2.1.2 逻辑代数的基本公式
真值表 利用基本定理化简公式 例：证明包含律
AB AC BC AB AC
证明：
AB（C C） AC(B B ) BC(A A) 1律、互补律 ABC ABC ABC ABC ABC ABC 分配律 ABC ABC ABC ABC 重叠律 AB AC 分配律、互补律
比较两种方法，应用反演规则比较方便。
2.1.3 逻辑代数的基本规则
2、反演规则
例题：求下列函数的反函数 1、F AB CD 2、F A B BCD
2.1.3 逻辑代数的基本规则
3、对偶规则
如果将逻辑函数F 中所有的“”变成“+”,“+”变
成“”,“0”变成“1”,“1”变成“0”, 则所得到的新
A
F
A1 F
非门 （A是输入，F是输出）
化简逻辑表达式的两种方法
化简逻辑表达式的两种方法
一、化简逻辑表达式的两种方法
1、用逻辑代数的方法：
逻辑代数是一种研究逻辑运算的代数化方法，它注重同类的因素合并成一项，若合并后的表达式和原表达式所表达的意义相同，则称此运算为化简。
用逻辑代数的方法来化简逻辑表达式，主要有三步：（1）使用逻辑乘除法和逻辑加括号法，将指定的逻辑表达式归
结成标准形式。
（2）使用合取范式和析取范式，进行逻辑替换，把可以合并的
项合并起来，使表达式简单易懂。
（3）根据合取定义和析取定义，继续合并，直到化简完毕。
2、用布尔代数的方法：
布尔代数是一种逻辑运算的代数，它将逻辑运算定义为一种操作，操作的运算结果可以是“真”和“假”的两种可能性。
使用布尔代数的方法来化简逻辑表达式，可以按照如下步骤：
（1）将逻辑表达式中的各个子式根据布尔代数中的定义转换成
有限的真值表式，也就是如01、0011、1111等等。
（2）利用真值表的合取规则，将真值表式中的项进行合并，最
终得到简化后的真值表式。
（3）根据简化的真值表式，化简出原来逻辑表达式中所包含的
逻辑操作关系，从而得出最终的结果。
- 1 -。
电工学2第11讲：逻辑代数-化简
（3）A A B A B A( A B) AB （4）
（5）AB ( AB ) A （6）( A B)( A B ) A 证： A AB
A AB AB A B
B 自己证明(提示：BC•1 ）
补： AB A C BC...... AB A C
1. 圈的个数应最少
2. 每个“圈”要最大 3. 每 “圈”至少 包含 一个未被圈过的最小项
i
写出简化逻辑式 Y A BD 如“0”特别少，也可圈0，但结果为 Y 。重做上题。
项少i个因子，填2 格
例4. 应用卡诺图化简逻辑函数
Y A B C A B C A BC AB B C
口诀： 圈大2n; 重复有新； 不拐不漏，边角为邻； 1原0反； 异去同存。
B取值（异）不同—“去” C、D同样
CD 00 AB 00 0 01 0
01 11 10
0 0 1 1
0 1 1 1
0 0 0 0
CD 00 AB 00 0
01 11 10
01 11 10
0 1 1 0
0 0 0 0
0 0 0 0
（2）配项法 例2： 化简 Y AB A C BC
AB A C BC ( A A ) AB ABC A C A BC AB A C
（3）加项法
例3： 化简 Y ABC A B C AB C
（4）吸收 例 4： 法 化简 Y AB AC BC
反演律
A B A B
A B
A B A B
A B 1 0 0 0
A B 1 1 1 0
列真值表证明：
A B
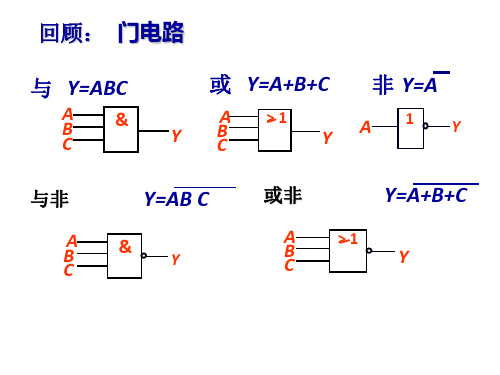
（5）AB ( AB ) A （6）( A B)( A B ) A 证： A AB
A AB AB A B
B 自己证明(提示：BC•1 ）
补： AB A C BC...... AB A C
1. 圈的个数应最少
2. 每个“圈”要最大 3. 每 “圈”至少 包含 一个未被圈过的最小项
i
写出简化逻辑式 Y A BD 如“0”特别少，也可圈0，但结果为 Y 。重做上题。
项少i个因子，填2 格
例4. 应用卡诺图化简逻辑函数
Y A B C A B C A BC AB B C
口诀： 圈大2n; 重复有新； 不拐不漏，边角为邻； 1原0反； 异去同存。
B取值（异）不同—“去” C、D同样
CD 00 AB 00 0 01 0
01 11 10
0 0 1 1
0 1 1 1
0 0 0 0
CD 00 AB 00 0
01 11 10
01 11 10
0 1 1 0
0 0 0 0
0 0 0 0
（2）配项法 例2： 化简 Y AB A C BC
AB A C BC ( A A ) AB ABC A C A BC AB A C
（3）加项法
例3： 化简 Y ABC A B C AB C
（4）吸收 例 4： 法 化简 Y AB AC BC
反演律
A B A B
A B
A B A B
A B 1 0 0 0
A B 1 1 1 0
列真值表证明：
A B
2 逻辑函数及其化简
=AB A B D A B D
AB A B ( D D )
AB AB
AB A B
A B &
&
AB
&
L
& &
AB
AB A B
（1-38）
利用逻辑代数的基本公式：
例2：
F ABC ABC ABC ABC AB (C C ) ABC AB 提出A A( BC B) A(C B) AC AB
A B( A A) A B
例如：A ABC DC A BC DC 被吸收
（1-17）
3.混合变量的吸收：
AB AC BC AB AC
1 证明： AB AC BC AB AC ( A A) BC
AB AC ABC ABC AB AC
普通代 数不适 用!
（1-15）
三、吸收规则 1.原变量的吸收： A+AB=A
证明：A+AB=A(1+B)=A•1=A
利用运算规则可以对逻辑式进行化简。 例如：
AB CD AB D( E F ) AB CD
被吸收
（1-16）
2.反变量的吸收：
A AB A B
证明：A AB A AB AB
2、逻辑函数的化简方法
化简的主要方法： １．公式法（代数法） ２．图解法（卡诺图法） 代数化简法： 运用逻辑代数的基本定律和恒等式进行化简的方法。 并项法:
A A 1
AB( C C ) AB
（1-36）
L AB C ABC
吸收法：
第2章 逻辑代数与逻辑化简
L ABC ABC ABC ABC
反之，由函数表达式也可以转换成真值表。 例2 写出函数 L A B
A B
真值表。
解：该函数有两个变量，有4种取值的可能 组合，将他们按顺序排列起来即得真值表。
逻辑函数及其表示方法（4）
3．逻辑图——逻辑图是由逻辑符号及它们之间的连线而构成的图形。 由函数表达式可以画出其相应的逻辑图。 例3 画出下列函数的逻辑图： 解：可用两个非门、两个与门 和一个或门组成。
∴等式成立 同理可得
AB A C BCD AB A C
逻辑代数的运算规则（4）
基本逻辑定理 （1）对偶定理 若已知等式
F G
1 0
F
1 0
0 1
" " " " " " " "
F
D
G
0 1
F的对偶式
" " " G的对偶式 " " " " "
L A B A B
由逻辑图也可以写出其相应 的函数表达式。 例4 写出如图所示逻辑图的函数表达式。 解：可由输入至输出逐步 写出逻辑表达式：
L AB BC AC
逻辑函数及其表示方法（5）
逻辑函数的标准形式 考查逻辑函数： F f ( A, B) AB AB AB 化简，有： 最小项 A AB 0 AB 0 AB 1 AB 1 B 0 1 0 1 标准“与或” 式
0 1 0 1
A 0 1
Y 1 0
0 1 0 1
&
≥1
A A
1
Y Y
逻辑 符号
逻辑代数的常用化简公式
逻辑代数的常⽤化简公式
1. 交换律： A+B=B+A;---@1 AB=BA;---@2
2. 结合律： (A+B)+C=A+(B+C);---@3 (AB)C=A(BC);---@4
3. 分配律： A(B+C)=AB+BC;---@5 A+BC=(A+B)(A+C);---@6
4. 吸收率： A+AB=A;---@7 A(A+B)=A;---@8
5. 其他常⽤：A+!AB=A+B;---@9 A(!A+B)=AB@10
以上逻辑运算基本定律中，恒等式⼤多是成对出现的，且具有对偶性。
⽤完全归纳法可以证明所列等式的正确性，⽅法是：列出等式的左边函数与右边函数的真值表，如果等式两边的真值表相同，说明等式成⽴。
但此⽅法较为笨拙，下⾯以代数⽅法证明其中⼏个较难证明的公式。
@7式证明：A+AB=A(1+B)=A;
@8式证明：A(A+B)=AA+AB=A+AB=A;由七式易得；
@6式证明：
A+BC=(A+AB)+BC;此处由@7式可得A=A+AB;
=A+AB+BC=A+B(A+C);此处由@5式可得AB+BC=B(A+C);
=A+AC+B(A+C);此处由@7式可得A=A+AC;
=A(A+C)+B(A+C);
=(A+B)(A+C); 得证。
@9式证明： A+!AB=A(1+B)+!AB;
=A+AB+!AB;
=A+B(A+!A);
=A+B;得证。
第四章：逻辑代数及其化简(4)
0 1 1 0
BC
F2
F = AB + C = AB + C = AB ⋅ C 1
F2 = BC + ABC = BC + ABC = BC ⋅ ABC 2、将 F1 和 F2 整体 化简(找公共项 找公共项） 找公共项
AB AB C 00 01 11 10 C 00 01 11 10 0 0 0 0 1 ABC 0 0 0 0 1 1 0 1 1 0 1 1 1 1 1 C
尾部代替因子 一个乘积项的尾部因子，可根据需要加以扩展，如果扩 展变量是属于头部内的变量，则该乘积项的值不变。扩展后 的因子，称为原乘积项尾部因子的代替因子。
Ei = abc = abac = abbc = ababc 头部因子可以随意放入尾部因子， 头部因子可以随意放入尾部因子，也可以从尾部因 子中取走。 子中取走。 即：尾部因子的反号可以任意伸长和缩短，伸长将头 部因子 放进去，缩短将头部因子取出来。
例： 证明： 证明： abc = abac = ab(a + c) = aba + abc = abc
abc = abbc = ab b + c = abc abc = ababc = ab a + b + c = abc
(
(
)
(a ⋅a = 0)
)
乘积项合并 如果两个或两个以上乘积项的头部完全相同，则这几个 乘机项可以合并为一个乘积项。 AB
例4:已知 F = ∑m(0,1,3,4,5)求F' 的最小项表达式。
F = B+ A C F' = B A + C = AB + BC
(
1 1 0 1 B = ABC + ABC + ABC A C = ∑m (0,1,5) F和F'号码数目相同，对应之和为7。 变量： F和F'之间的关系： 由此推广到 n 变量： ) F = ∑m (0,1,3,4,5) F( a, b, cL = ∑( i) 最小项编号
第四章：逻辑代数及其化简(2)
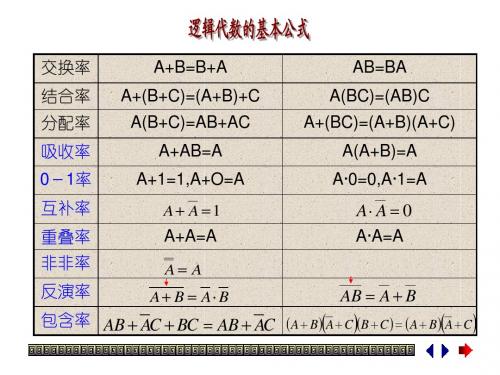
包含律：AB AC BC AB AC 证：AB AC BC AB AC A ABC
AB AC ABC ABC
AB1 C AC 1 B
若两个乘积项中分别 包含A和A两个因子， 而这两个乘积项的其 余因子组成第三个乘 积项，则第三个乘积 项是多余的。可消去
定理：任何逻辑函数 F 都可以用最小项之和的形式表示。 而且这种形式是唯一的。 1、 真值表法： 将逻辑函数先用真值表表示，然后再根据真值表写出最 小项之和。 例：将 F ABC BC AC 表示为最小项之和的形式。 解：由最小项特点知：n 个变量都出现，BC 缺变量 A ,
AC缺变量B, BC和AC不是最小项。 所以 F 是一般与－或式，不是最小项之和的标准形式。
例：已知一个奇偶判别函数的真值表（偶 ③ n个输入变量就有2n个 为1,奇为0)，试写出它的逻辑函数式。
A 0 0 0
B 0 0 1
C 0 1 0
Y
0
1 1
1
0 0
1
0 1
1
1
0
解： 当ABC=011时， 使乘积项 ABC 1 1 1 1 不同的取值组合。 当ABC=101时， 使乘积项ABC 1 当ABC=110时， 使乘积项ABC 1 因此，Y的逻辑函数应当等于这三个乘积项之和。 Y ABC ABC ABC
二、从逻辑表达式列出真值表 将输入变量的所有状态组合 逐一代入逻辑式，求出函数值， 列成表，即可得到真值表。 例：已知函数 Y A BC ABC 求其对应真值表。 解：将三变量所有取值组合代 入Y式中，将计算结果列表。
A B C 0 0 0 0 0 1
BC
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
础
第
二
章 电子学教研室
38
2020/5/16
数 与或表达式： F AB ACD
字 电
标准与或表达式：F ABCD ABCD ABCD
子 或与表达式： F ( A B)(A C D)
技 术
标准或与表达式: F (A B C D)(A B C D)(A B C D)
1
数 字
A
0 m0 m1
电
1 m2 m3
子
技
术
BC 00 01 11
基 础
A
0 m0 m1 m3
第
1 m4 m5 m7
二
章 电子学教研室
CD AB
00
01
11
10
00 m0 m1 m3 m2
01 m4 m5 m7 m6
11 m12 m13 m15 m14
10 m8 m9 m11 m10
10
m2
方格中脚标数字为 对应最小项编号。
子
选定某种进位的计数制来表示某个数的值
技
术 按“形”表示 编码 （Encode）
基
用代码来表示某些数的“值”
础 先要确定编码规则，然后按此编码规则编
第
二 出代码，并给代码赋以一定的含义
章 电子学教研室
2
2020/5/16
常用计数制及其转换
数 字 电 子 技 术 基 础
第 二 章 电子学教研室
自学
3
章 电子学教研室
12
2020/5/16
数 3）逻辑符号
字 电
在数字电路中，实现逻辑与运算的单元
子 电路叫与门。
技
术
与门的逻辑符号
基
A&
F B
础 本教材采用的逻辑符号
第
A B
F
二
章 电子学教研室
13
2020/5/16
或运算
数
在决定一事件发生的多个条件中，只
字 电 要有一个条件满足，此事件就会发生。
技
术 基
F D A D(B C)
础
第
二
章 电子学教研室
34
2020/5/16
数 3 对偶规则
字
对于一个逻辑函数式F,若将其中的
电 子
0 1, 1 0,
技
,
术
则得到的结果就是F的对偶式
基 础
F F
若两逻辑式相等,则它们的对偶式也相等。
第
二
章 电子学教研室
35
2020/5/16
练习
子
技
A
术
B
基
础
F
E
第
二
章 电子学教研室
14
2020/5/16
数 1）真值表
字
逻辑或运算的真值表
电
子
AB F
技
00 0
术
10 1
基
01 1
础
11 1
第
二
章 电子学教研室
15
2020/5/16
数 2）逻辑函数表达式
字
表示逻辑或运算的逻辑函数表达式为
电 子
F＝A+B
技
“+”为或运算符号
术
不可以省略
基 础
AB, AB, AB, AB
44
2020/5/16
最小项编号
数
字 最小项
ABC ABC ABC ABC ABC ABC ABC ABC
电 子 二进制代码 000 001 010 011 100 101 110 111
技 术 十进制数 0 1 2 3 4 5 6 7
基 础
mi
m0 m1 m2 m3 m4 m5 m6 m7
二
章 电子学教研室
32
2020/5/16
数 2. 反演规则
字
对于一个逻辑函数式F,若将其中所有的
电 子
0 1, 1 0,
技
,
术 基 础
A A, A A
则得到的结果就是F的反函数
第
FF
二
章 电子学教研室
33
2020/5/16
数 注意：优先顺序不能变，帽子以上不能变。
字
电 子
例 F D A D BC
第 推论：AB AC BCDEF（K ） AB AC
二
章 电子学教研室
29
2020/5/16
数
5. AB AB A
字
电
子
6. (A B)( A B) A
技
术
基
础
第
二
章 电子学教研室
30
2020/5/16
*异或公式(补充)
数 A0 A
字 电
A1 A
子 A A0
技 术
A A 1
基 A B A B A B A B 1
础
第
二
章 电子学教研室
8
2020/5/16
逻辑代数的基本运算和复合运算
数
逻辑代数的基本运算包括与、或、非三
字 电 种运算。
子
设开关A、B为逻辑变量，约定开关闭
技
术 合为逻辑1、开关断开为逻辑0；设灯为逻
基 础
辑函数F，约定灯亮为逻辑1，灯灭为逻辑
第 0。
二
章 电子学教研室
9
2020/5/16
与运算
m6 每一个方格内mn取
值为0或1。
43
最小项-标准与或表达式
数
标准与或表达式是一种特殊的与或表达
字 式，其中的每个与项都包含了所有相关的
电 子
逻辑变量，每个变量以原变量或反变量出
技 现一次且仅出现一次，这样的与项称为标
术 准与项，又称最小项。
基
础
如 F=F(A, B)，共有最小项4项：
第 二 章 电子学教研室
础
01
1
第
10
1
二
11
0
A B
F
章 电子学教研室
21
2020/5/16
数 2）或非运算
字
电
子
AB F
技
00
1
术
01
0
基
10
0
础
11
0
第 二 章 电子学教研室
F AB
A ≥1
F B
A B
F
22
2020/5/16
数 3）与或非运算
字
电 F A•BC•D
子 技 术
A & ≥1
B C
F
D
基
础
A B
F
B
基
F
础
第
二 章 电子学教研室
C D
41
2020/5/16
4 卡诺图
数
将逻辑变量分成两组，分别在横竖两个
字 电 方向排列出各组变量的所有取值组合，构
子 成一个有2n个方格的图形，其中，每一个
技 术 方格对应变量的一个取值组合，这种图形
基 叫做卡诺图。
础
第
二
章 电子学教研室
42
2020/5/16
B0
数
字 Y AB B AB A B
电
子 Y AC AB B C AC BC
技
术 基
Y ABCD ABCD A
础
Y (A BC)(A BC） A
第
二
章 电子学教研室
36
2020/5/16
2.3 逻辑函数常用的描述方法及相互间的转换
数 逻辑函数常用的描述方法
字
电
逻辑表达式
子
真值表
基 与非与非表达式: F ABCD 础 第 或非或非表达式: F A B C D
二 与或非表达式： F AB CD
章 电子学教研室
39
2020/5/16
ABC F
2 真值表
0
0
0
0
0
0
1
1
数
用来反映变量所有取值00组合及11 对应01 函数10
字 电
值的表格，称为真值表。 1 1
0 0
子 技
所谓二-十进制码，就是用4位二进制数
术 组成的代码来表示1位十进制数。
基
础
第
二
章 电子学教研室
5
2020/5/16
数 4位二进制数具有16种组合，二-十进制
字 数的10个数字符号只需选用其中的10种组
电 子
合来表示常用的几种二-十进制编码表2-1
技 所示。
术
基
础
第
二
章 电子学教研室
6
2020/5/16
技
术
AB F
基 础
00 0 10 0
逻辑与运算的真值表
01 0
第 二
11 1
章 电子学教研室
11
2020/5/16
数 2）逻辑函数表达式
字
表示逻辑与运算的逻辑函数表达式为
电 子
F＝A ·B
技
“·”为与运算符号
术
也可以省略
基 础
与运算规则为： 0·0＝0
0·1＝0
第
1·0＝0 1·1＝1
二 可推广到多变量： F＝A·B·C·D···
非运算
数 当条件不具备时，事件才会发生。
字
电
子
技
R
术
E
基
A
F
础
第
二
章 电子学教研室
18
2020/5/16
数 1）真值表