2014初中数学青年教师解题大赛试题参考答案
2014年惠阳区数学青年教师解题比赛训练题(三)答案

2014年惠阳区数学青年教师解题比赛训练题(三)参考答案及评分标准说明:1本参考答案及评分标准仅供教师评卷时参考使用.2其它正确的证法(解法),可参照本参考答案及评分标准酌情赋分. 一、选择题(每小题3分,共30分)1.A2.C3.C4.B5.D6.A7.D8.C9.A 10.B 二、填空题(每小题3分,共24分)11. 01≠-≥x x 且 12. 2 13. 300π 14. 2 15. 61255=-x x 16. 4 17.251218.)0,22( 或)0,22(- 三、解答题(19小题9分,20小题9分,共18分) 19.解: a a aa a a 1)22(2-÷--- =()122-⨯⎥⎦⎤⎢⎣⎡---a aa a a a …………………………1分 =11-⨯⎪⎭⎫ ⎝⎛-a aa a …………………………2分 =112-⨯-a aa a ……………………………4分 =()()111-⨯-+a aaa a ……………………………5分 =1+a …………………………6分当a = 45tan 211-⎪⎭⎫⎝⎛-°=2-1=1时;原式分母为零 …………………………8分原式无意义 …………………………9分 20. 解:(1)∵点),1(a A 在xy 3=的图象上, ∴13=a =3 ……………2分∴点)3,1(A ……………3分第二次第一次C A 2A 2A 2A 2A 1A 1A 1A 1C B B C B CB 开始(2)∵△ABO 向右平移2个单位长度,得到△DEF∴D (3,3) ……………6分 ∵点D 在)0(>=x xky 的图象上, ∴3=3k ……………8分∴k =9 ……………9分四、解答题(本题14分)21.解:(1)解法一:70÷360126=200(名),本次调查了200名学生 ……2分 解法二:设共有x 名学生,12636070=x 解得200=x (2)……………………7分(每空1分)(3)(0.21+0.35)×1500=840(名) ……………………8分答:该校学生整理错题集情况非常好和较好学生人数一共约有840名 …………………9分 (4)解: 解法一:画树形图如下:……………10分HGA BEDFC……………………12分由树形图可知,所有可能出现的结果有12种,且每种结果出现的可能性相等,其中两次抽到的错题集都“非常好”的有2种; ………………13分 ∴P (两次抽到的错题集都“非常好”)=122=61………………………14分 解法二:列表如下…………12分由表可知,所有可能出现的结果有12种,且每种结果出现的可能性相等,其中两次抽到的错题集都“非常好”的有2种; ……………………13分∴P (两次抽到的错题集都“非常好”)=122=61………………………14分 五、解答题(22、23小题各12分,共24分) 22.解:延长AD 交EF 于点G ,过点B 作BH ⊥AG ,垂足为H . ……1分 ∵BE 、CF 关于AD 轴对称,EF =6 ∴EG =21EF =3 …………………2分 ∵四边形BEGH 是矩形∴BH =EG =3 ………………………………3分 在Rt △ABH 中,AH =BH 30tan ⋅°=3×33=3 ……………6分 DH =AD -AH =33- …………………7分 在Rt △DEG 中,DG =EG 20tan ⋅°≈3×0.36=1.08 ………10分∴BE =HG =DH +DG =33-+1.08≈3-1.73+1.08≈2.4(米) 答:仓库设计中BE 的高度约为2.4米.……12分23.解:(1)设⊙O 的半径为r∵BE =2,DG =3∴OE =r +2,OG =r +3 ………………………………1分∵EF ⊥AB∴∠AEG =90°在Rt △OEG 中,根据勾股定理得,222OG EG OE =+ ………………………………2分 ∴222)3(3)2(r r +=++………………………………3分 解得:2=r ………………………………5分(2)∵EF =2,EG =3∴FG =EF +EG =3+2=5∵DG =3,OD =2,∴OG =DG +OD =3+2=5 ………………………………6分 ∴FG =OG ………………………………7分∵DG =EG ,∠G =∠G∴△DFG ≌△E 0G ………………………………9分∴∠FDG =∠OEG =90° ………………………………10分 ∴DF ⊥OD ………………………………11分 ∴DF 是⊙O 的切线 ………………………………12分PFEDCBA六、解答题(本题12分)24.解:(1)设大枣粽子每盒x 元,普通粽子每盒y 元, 根据题意得⎩⎨⎧=-=+1530042y x y x …………………………………………………1分 解得:⎩⎨⎧==4560y x (用一元一次方程求解赋相同的分) ……………2分答:大枣粽子每盒60元,普通粽子每盒45 元. ……………3分 (2)解:①W =1240-60x -45(20-x )= -15x +340 ……………………5分②根据题意,得⎩⎨⎧≤+-≥+-2403401518034015x x …………………………………………………6分 解得326≤x ≤3210 …………………8分 ∵x 是整数∴x 取7,8,9,10∴20-x 取13,12,11,10 …………………9分 共有四种购买方案:方案:①购买大枣粽子7盒,普通粽子13盒②购买大枣粽子8盒,普通粽子12盒 ③购买大枣粽子9盒,普通粽子11盒④购买大枣粽子10盒,普通粽子10盒 …………………11分 根据一次函数性质, ∵015<-=k ∴W 随x 的减小而增大 ∴x =7时W 有最大值∴购买大枣粽子7盒,普通粽子13盒时,购买水果的钱数最多. ……12分七、解答题(本题14分)25.(1)证法一:如图① ∵四边形ABCD 是正方形, ∴AB =BC ,∠ABC =∠PBA =90°CA PF E DBGPFEDCBA又∵BP =BF∴△PBA ≌△FBC ……………1分 ∴P A =FC ∠P AB =∠FCB又∵P A =PE ∴PE =FC ……………2分∵∠P AB +∠APB = 90° 第25题 图① ∴∠FCB +∠APB = 90° 又∵∠EP A =90°∴∠APB +∠EP A +∠FPC =180° 即∠EPC +∠PCF =180°∴EP ∥FC ………………4分 ∴四边形EPCF 是平行四边形. ………………5分证法二:延长CF 与AP 相交于点G ,如图②∵四边形ABCD 是正方形,∴AB =BC , ∠ABC =∠PBA =90° 又∵BP =BF∴△PBA ≌△FCB ……………1分 第26题 图②∴∠P AB =∠FCB ,AP =CF又∵P A =PE ∴PE =FC ……………2分∵∠P AB +∠APB =90°∴∠FCB +∠APB =90°∴∠PGC =90°∴∠PGC =∠APE =90°∴EP ∥FC ……4分∴四边形EPCF 是平行四边形. ………5分(2)证法一:结论:四边形EPCF 是平行四边形,如图③ ……6分∵四边形ABCD 是正方形,∴AB =BC , ∠ABC =∠CBF =90°又∵BP =BF ∴△PBA ≌△FBC ……………7分∴P A =FC ∠P AB =∠FCB又∵P A =PE ∴PE =FC ……………8分GCAPFEDB ∵∠FCB +∠BFC = 90°∠EPB +∠APB = 90° 第25题图③ ∴∠BPE =∠FCB∴EP ∥FC ………………9分 ∴四边形EPCF 是平行四边形. ………………10分 证法二:结论:四边形EPCF 是平行四边形 ……………6分 延长AP 与FC 相交于点G 如图④ ∵四边形ABC D 是正方形,∴AB =BC , ∠ABC =∠CBF =90°又∵BP =BF ∴△PBA ≌△FBC ……………7分 ∴P A =FC ∠P AB =∠FCB又∵P A =PE ∴PE =FC ……………8分 ∵∠FCB +∠BFC =90° ∴∠P AB +∠BFC =90° ∴∠PGF =90° ∴∠PGF =∠APE =90°∴EP ∥FC ………………9分 第25题④图 ∴四边形EPCF 是平行四边形. ………………10分(3)解:设BP =x ,则PC =3-x 平行四边形PEFC 的面积为S , …………………11分S =PC ·BF =PC ·PB =()49233322+⎪⎭⎫ ⎝⎛--=+-=-x x x x x ……………12分当23=x 时, 最大s =49…………………………………………………13分 ∴当BP =23时,四边形PCFE 的面积最大,最大值为49. …………………14分八、解答题(本题14分)26.解:(1)由抛物线经过点A (-1,0)、B (3,0)得,⎩⎨⎧=++=+-033903b a b a ………………………………………………………1分解得,⎩⎨⎧=-=21b a ∴抛物线的解析式为322++-=x x y ; …………2分(2)解法一: 设点P (m ,0)∵点P 在抛物线322++-=x x y 上, ∴PE =322++-m m把0=x 代入322++-=x x y 得, 3=y ∴C (0,3) ……3分 设直线BC 解析式为b kx y +=,则⎩⎨⎧==+33b b k 解得⎩⎨⎧=-=31b k ∴直线BC 解析式为3+-=x y …………4分 第26题 图①∵点F 在直线BC 上,∴PF =3+-=m∴EF =PE -PF =m m 32+-= ……………………………5分 若四边形ODEF 是平行四边形,则EF =OD =2∴232=+-m m , ……………………………6分 解得 2,121==m m ………………………………7∴P (1,0)或 P (2,0) ………………………8解法二:如图②把0=x 代入322++-=x x y 得, 3=y ∴C (0,3)设直线BC 解析式为b kx y +=,则⎩⎨⎧==+33b b k 第26题 图②解得⎩⎨⎧=-=31b k∴直线BC 解析式为3+-=x y …………3分 过点D 作DG ⊥EF 于点G ,则四边形ODGP 是矩形 ∴DG =OP若四边形ODEF 是平行四边形 ∴DE ∥OF ∴∠DEF =∠OFP ∵∠DGE =∠OPF =90° ∴△DEG ≌△OFP∴EG =FP ………………4分 设点P (m ,0)∵点P 在抛物线322++-=x x y 上, ∴PE =322++-m m ………………5分 ∵点F 在直线BC 上,∴PF 3+-=m ∵EG =2322-++-m m =122++-m m∴122++-m m =3+-=m ……………………6分∴232=+-m m ,解得 2,121==m m ………7分 ∴P (1,0)或 P (2,0) …………………8分 (3)当点P (2,0)时,即OP =2,如图③连接DF 、OE 相交于点G ,取OP 的中点H ,连接GH∵四边形ODEF 是平行四边形 ∴OG =GE∴GH 是△OEP 的中位线∴GH ∥EP ,GH =21PE把x =2代入322++-=x x y 得,3=y ,即PE =3∴GH =23第26题图③∵GH ∥EP ∴GH ⊥OP ∴G (1,23) ……………………9分 设直线AG 的解析式为11b x k y +=,则⎪⎩⎪⎨⎧=+-=+0231111b k b k , ……………………10分解得⎪⎪⎩⎪⎪⎨⎧==434311b k∴将平行四边形ODEF 的面积等分的直线解析式为4343+=x y …11分 当点P (1,0)时,即OP =1,如图④连接DF 、OE 相交于点G ,取OP 的中点H ,连接GH ,∵四边形ODEF 是平行四边形 ∴OG =GE∵OH =HP =21OP =21∴GH 是△OEP 的中位线 ∴GH ∥EP ,GH =21PE 把x =1代入322++-=x x y 得,4=y ,即PE =4 第26题 ④图 ∴GH =2 ∵GH ∥EP ∴∠GHO =∠EPO =90° ∴G (21,2) ……………………12分 设直线AG 的解析式为22b x k y +=,则⎪⎩⎪⎨⎧=+-=+02212222b k b k ……………………13分 解得⎪⎪⎩⎪⎪⎨⎧==343422b k ∴将平行四边形ODEF 的面积等分的直线解析式为3434+=x y 综上所述,直线解析式为 4343+=x y 或 3434+=x y …14分。
2014年长沙市首届中学数学教师解题能力大赛(初中试题)答案

3
x
点,且 AM ⋅ AN = 4 ,则 k =
. ( 3)
18. 已知线段 AB 的中点为 C,以点 A 为圆心,AB 的长为半径作圆,在线段 AB 的延长线上 取点 D,使得 BD=AC;再以点 D 为圆心,DA 的长为半径作圆,与⊙A 分别相交于 F,
AH
G 两点,连接 FG 交 AB 于点 H,则 AB 的值为
——6 分
解之得到: x = 50 2
——8 分
故信号兵跑的距离为 s = 100 + 2x = 100(1+ 2) 米
——9 分
24.(满分 9 分)如图,已知:C 是以 AB 为直径的半圆 O 上一点,CH⊥AB 于点 H,直线 AC 与过 B 点的切线相交于点 D,E 为 CH 中点,连接 AE 并延长交 BD 于点 F,直线 CF 交 直线 AB 于点 G. (1)求证:点 F 是 BD 中点; (2)求证:CG 是⊙O 的切线; (3)若 FB=FE=2,求⊙O 的半径.
⎧2a − b < 或 ⎪⎪⎨a < 3 ,
⎪2 ⎪⎩b > 3.
0,
由 a , b 的实际意义为 1,2,3,4,5,6,可得
⎧a ⎨⎩b
= =
2,3,4,5,6,
共有
1,2,
5×2=10
种情况;或
⎧a ⎨⎩b
= =
1,
共
4,5,6,
3
种情况.
又掷两次骰子出现的基本事件共 6×6=36 种情况,故所求的概率为 13 . 36
(1)样本的容量是多少?
(2)通过计算说明样本数据中,中位数落在哪个组,并求该小组
的频率;
(3)估计全校在这次竞赛中,成绩高于 70 分的 学生人数占参赛人
2014年青年教师素质考试数学试题(含答案)
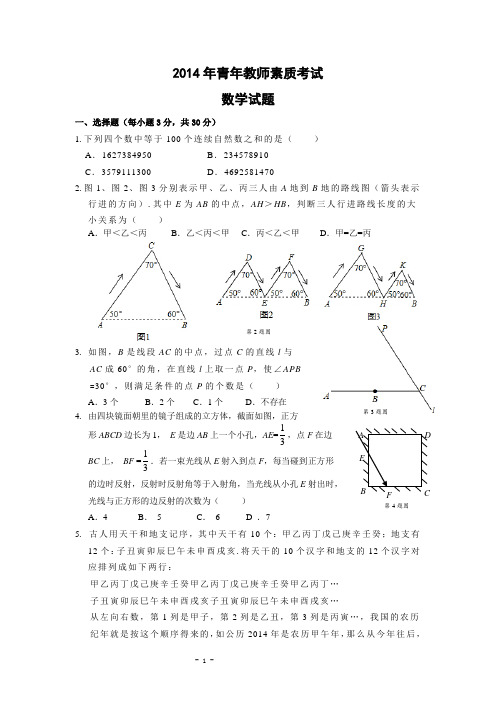
第2题图2014年青年教师素质考试数学试题一、选择题(每小题3分,共30分)1.下列四个数中等于100个连续自然数之和的是( ) A .1627384950 B .234578910C .3579111300D .46925814702.图1、图2、图3分别表示甲、乙、丙三人由A 地到B 地的路线图(箭头表示行进的方向).其中E 为AB 的中点,AH >HB ,判断三人行进路线长度的大小关系为( ) A .甲<乙<丙 B .乙<丙<甲 C .丙<乙<甲 D .甲=乙=丙3. 如图,B 是线段AC 的中点,过点C 的直线l 与AC 成60°的角,在直线l 上取一点P ,使∠APB =30°,则满足条件的点P 的个数是( ) A .3个 B .2个 C .1个 D .不存在 4. 由四块镜面朝里的镜子组成的立方体,截面如图,正方 形ABCD 边长为1, E 是边AB 上一个小孔,AE =31,点F 在边 BC 上, BF =31.若一束光线从E 射入到点F ,每当碰到正方形 的边时反射,反射时反射角等于入射角,当光线从小孔E 射出时, 光线与正方形的边反射的次数为( ) A .4 B . 5 C . 6 D .75. 古人用天干和地支记序,其中天干有10个:甲乙丙丁戊己庚辛壬癸;地支有12个:子丑寅卯辰巳午未申酉戌亥.将天干的10个汉字和地支的12个汉字对应排列成如下两行:甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸甲乙丙丁… 子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申酉戌亥…从左向右数,第1列是甲子,第2列是乙丑,第3列是丙寅…,我国的农历 纪年就是按这个顺序得来的,如公历2014年是农历甲午年,那么从今年往后,A BCDEF第4题图第3题图如果按出发到现在的平均速度继续行驶,那么还有1个小时到达乙地.第8题图MQPA 1BN 第12题图农历纪年为甲亥年的那一年在公历中( ) A .是2018年 B .是2031年 C .是2044年D .没有对应的年号6. 将正三角形每条边四等份,然后过这些分点作平行于其它两边的直线,则以图中线段为边的菱形个数为( ) A .15B .18C .21D .247. 工地上有甲、乙二块铁板,铁板甲形状为等腰三角形,顶角为α,且tan α=34,腰长为6cm ;铁板乙形状为等腰梯形,两底边长分别为4cm ,10cm ,且有一内角为60°.现在我们把它们任意翻转,分别试图从一个直径为5.3cm 的铜环中穿过,结果是( )A .甲板能穿过,乙板不能穿过;B .甲板不能穿过,乙板能穿过C .甲、乙两板都能穿过D .甲、乙两板都不能穿过 8. 如图,在边长为1的正方形ABCD 中,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 上的点,3AE =EB ,有一只蚂蚁从 E 点出发,经过F ,G ,H ,最后回点E 点,则蚂蚁所 走的最小路程是( )A .2B .4C .22D .32 9. 甲、乙两地相距250公里,某天小敏从上午7:50由甲地开车前往乙地办事. 在上午9:00,10:00,11:00三个时 刻,车上的导航仪都进行了提示(如图).假设导航仪提示语都是正确的,那么在上午11:00时,小敏距乙地还有( ) A .60公里 B .45公里 C .30公里 D .15公里 10. 如图,在Rt △ABC 中,∠ABC 是直角,AB =3,BC =4,P是BC 边上的动点.设BP =x ,若能在AC 边上找到一点 Q ,使∠BQP =90°,则x 的取值范围是( ) A .2.4≤x ≤4 B .3≤x ≤4C .2.5≤x ≤4D .3<x ≤4二、填空题(每小题3分, 共18分)11. 如图,在Rt △ABC 中,∠ACB =90°,∠B =30°,以点A 为圆心,BC 长为半径画弧;以点B 为圆心,AC 长为 半径画弧,两弧交于点D ,连结CD .若AC =1,则CD 的长度是 .12. 如图,边长为1的正三角形ANB 放置在边长为MN =3,NP =4的长方形MNPQ 内,且NB 在边NP 上.若正三第10题图 第6题图AFGHD CE 第13题图第16题图角形在长方形内沿着边NP 、PQ 、QM 、MN 翻转一圈后回到原来起始位置,则顶点A 在翻转过程中经过的路程长是 (保留π). 13. 如图,一个半径为1的圆纸片,第一次剪去半径为12的圆,得到的图形P 1的面积为S 1,第二次剪去半径为14的圆,得到的图形P 2的面积为S 2,第三次剪去半径为18的圆,得到的图形P 3的面积为S 3,…,依此,第n 次剪完后得到的图形P n 的面积为S n 则S 2013-S 2014= .14. 2014年仁川亚运会期间,体育场馆要对观众进行安全检查.若某体育馆在安检开始时已有若干名观众在馆外等候安检,安检开始后,到达体育馆的观众人数按固定速度增加.各安检人员的安检效率相同.若用3名工作人员进行安检,需要25分钟才能将等候在馆外的观众检测完,使后来者能随到随检;若用6名工作人员进行安检,时间则缩短为10分钟.现要求不超过5分钟完成上述过程,则至少要安排 名工作人员进行安检.15. 现有红、黄、蓝、白4种颜色的袜子若干(足够多),若只要两只同色的袜子就可以配成1双,请问至少需要 只袜子就一定能够配成10双袜子. 16. 如图,一个直角边长为2的等腰直角三角形纸片,D 为直角边BC 上一点,首先把点B折叠到点D ,再把点A 折叠到点D ,使△CDE 与△DFG 的面积相等,则CD 的长度 为三、解答题(本大题有6小题,第17小题6分,第18、19小题每小题8分,第20、21、22小题10分,共52分.解答需写出必要的文字说明、演算步骤或证明过程) 17. 一场数学游戏在两个非常聪明的学生甲、乙之间进行.裁判先在黑板上写出下面的正整数2,3,4,…,2006,然后随意擦去一个数.接下来由乙、甲两人轮流擦去其中的一个数(即乙先擦去其中的一个数,然后甲再擦去一个数,如此轮流下去),若最后剩下的两个数互质,则判甲胜;否则,判乙胜. 按照这种游戏规则,甲、乙两人获胜的机会均等吗?并求甲获胜的概率.18.如图,△ABC中,∠BAC=60°,AB=2AC.点P在△ABC内,且PA=3,PB=5,PC=2,求△ABC的面积.第18题图19.有8个人乘速度相同的两辆小汽车同时赶往火车站,每辆车乘4人(不包括司机),其中一辆小汽车在距离火车站15km的地方出现故障,此时距停止检票的时间还有42分钟.这时唯一可利用的交通工具是另一辆小汽车,已知包括司机在内这辆车限乘5人,且这辆车的平均速度是60km/h,人步行的平均速度是5km/h.试设计两种方案,通过计算说明这8个人能够在停止检票前赶到火车站.20.在Rt△ABC中,∠BAC=90°, AB=AC=2,点D在BC所在的直线上运动,作∠ADE=45°(A,D,E按逆时针方向).(1)在图1,若点D在线段BC上运动,DE交AC于E. 易证:△ABD∽△DCE; 当AD =DE时,求AE的长.(2)①在图2,若点D在边BC的延长线上运动,DE的反向延长线与AC的延长线相交于点F,是否存在点D,使AD=DF?若存在,写出CD的长; 若不存在,请说明理由.②在图3,若点D在边BC的反向延长线上运动,DE与AC的延长线相交于E点,是否存在点D,使AD=DE?若存在,写出所有点D的位置; 若不存在,请说明理由.第20题图21.如图,在直角坐标系中,四边形OABC为矩形,A(8,0),C(0,6),点M是OA的中点,P、Q两点同时从点M出发,点P沿x轴向右运动;点Q 沿x轴先向左运动至原点O后,再向右运动到点M停止,点P随之停止运动.P,Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与矩形OABC重叠部分(阴影部分)的面积为S(平方单位).(1)用含t的代数式表示点P的坐标.(2)分别求当t=1,t=5时,线段PQ的长.(3)求S与t之间的函数关系式.(4)连接AC.当正方形PRLQ与△ABC的重叠部分为三角形时,直接写出t的取值范围.第21题图22.如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.(1)求抛物线的解析式.(2)是否存在点P,使得△ACP是直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.第22题图数学参考答案1.A2. D3. B4. B5.D6. C7. C8.C9.A 10.B 11.1或2 12. 5π 13. 40282π14. 11 15.23 16. 222-17.18.19. 解:[方案一]:当小汽车出现故障时,乘这辆车的4个人下车步行,另一辆车将车内的4个人送到火车站,立即返回接步行的4个人到火车站. 设乘出现故障汽车的4个人步行的距离为xkm ,根据题意,有6015155x x -+= 解得1330=x ,因此这8个人全部到火车站所需时间为()(分钟)(分钟)=小时4213540523560)133015(51330<=÷-+÷ 故此方案可行.[方案二]:当小汽车出现故障时,乘这辆车的4个人下车步行,另一辆车将车内的4个人送到某地方后,让他们下车步行,再立即返回接出故障汽车而步行的另外4个人,使得两批人员最后同时到达车站.分析此方案可知,两批人员步行的距离相同,设这个路程为y 千米,60215155yy y -+-=解得2=y 。
2014年惠阳区初中数学教师解题比赛参考答案及评分标准

2014年惠阳区初中数学教师解题比赛参考答案及评分标准一.选择题(本大题共10小题,每小题3分,共30分)1A 2、D 3A 4B 5、D 6.B 7.D 8.D 9、B 10.C二.填空题(本大题共6小题,每小题4分,共24分)11、(-2,0)(3,0) 12、球或正方体 13、4:3 14.))(c b a b a +++( 15.8. 16.46 三、解答题(一)(本大题共3小题,每小题6分,共18分)17. 解:(1)设彩色地砖采购x 块,单色地砖采购y 块,由题意,得 … .. … … 1分, ………………2分 解得:.答:彩色地砖采购40块,单色地砖采购60块; ……………………4分(2)设购进彩色地砖a 块,则单色地砖购进(60﹣a )块,由题意,得80a +40(60﹣a )≤3200, ……………………5分 解得:a ≤20.∴彩色地砖最多能采购20块 ……………………6分18.(1)点A 关于y 轴对称的点的坐标(2,3); … .. … … 1分(2)图形. … .. … … 3分 点B 的对应点的坐标(0,6-); … .. … … 4分(3)第四个顶点D 的坐标(7-3,)或(53)--,或(33), … .. … … 6分19.解:(1)∵),1(b 在直线1+=x y 上,∴当1=x 时,211=+=b . …………2分(2)解是⎩⎨⎧==.2,1y x ……………4分 (3)直线m nx y +=也经过点P ……………5分∵点P )2,1(在直线n mx y +=上,∴2=+n m ,∴21n m =⨯+,这说明直线m nx y +=也经过点P .………6分四、解答题(二)(本大题共3小题,每小题7分,共21分)20.解:(1):80,20,72; … .. … … 3分(2)骑自行车的人数为:80×20%=16人,补全统计图如图所示; ………4分(3)设原来开私家车的人中有x 人改为骑自行车, 由题意得,×2000+x ≥×2000﹣x ,解x ≥50, …………6分答:原来开私家车的人中至少有50人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数. …………7分21:(1)∵DC ⊥AE ,BA ⊥AE ∴△ECD ∽△EAB …………1分 ∴bc c AB a ,AE CE AB CE +==即 ……………2分 ∴c ab a c b c a AB +=+=)( ………………3分 (2)∵AE ⊥AB ,DC ⊥AB ,DE ⊥AE∴DC =AE =n ,AC =DE =m ……………4分 在Rt △DBC 中,BC /CD =tanα, ……………5分 ∴BC =n ·tanα ……………6分 ∴AB =BC +AC =n ·tanα+m ……………7分22. 解:1)∵在矩形ABCD 中,AB =2DA ,DA =2, …………1分 ∴AB =AE =4, ∴DE ==2, …………2分 ∴EC =CD ﹣DE =4﹣2; …………3分(2)∵sin ∠DEA ==, ∴∠DEA =30°, ∴∠EAB =30°, …………4分 ∴图中阴影部分的面积为:S 扇形F AB ﹣S △DAE ﹣S 扇形EAB …………5分 =﹣×2×2﹣=﹣2 ………………7分五、解答题(三)(本大题共3小题,每小题9分,共27分)23.解:(1)由0y =,得2x =-,所以点A 的坐标为(20)-,,故2OA = ……1分 同理可得4OB =. ……2分所以在Rt AOB △中,AB = ……3分(2)作MP x ⊥轴,NP y ⊥轴,MP 交NP 于点P .则MP NP ⊥,P 点坐标为(31)-,. ……4分故4(1)5PM =--=,3(2)5PN =--=. ……5分所以在Rt MPN △中,MN ==. ……6分 (注:若直接运用了(3)的结论不得分.)(3)作2P P x ⊥轴,1PP y ⊥轴,2P P 交1PP 于点P . 则21P P PP ⊥,点P 的坐标为21()x y ,. ……7分 故221P P y y =-,121PP x x =-(不加绝对值符号此处不扣分).……8分所以在21Rt P PP △中,12PP =……9分 24.解:(1)∵四边形ABCD 是正方形,∴AD ∥BF ,……1分 ∵AE =CF ,∴四边形ACFE 是平行四边形,∴EF ∥AC ,……2分 (2)连接BG ,∵EF ∥AC ,∴∠F =∠ACB =45°,……3分 ∵∠GCF =90°,∴∠CGF =∠F =45°,∴CG =CF ,……4分∵AE =CF ,∴AE =CG ,在△BAE 与△BCG 中,,∴△BAE ≌△BCG (SAS )∴BE =BG ,……5分 ∵BE =EG ,∴△BEG 是等边三角形,∴∠BEF =60°,(3)∵△BAE ≌△BCG ,∴∠ABE =∠CBG ,∵∠BAC =∠F =45°,∴△AHB ∽△FGB ,……6分∴======,……7分 ∵∠EBG =60°∠ABE =∠CBG ,∠ABC =90°,∴∠ABE =15°,……8分 ∴=.……9分25. 解:(1)∵y=x2﹣x﹣3,∴当y=0时,y=x2﹣x﹣3,……1分解得x1=﹣2,x2=4.当x=0,y=﹣3.∴A点坐标为(4,0),D点坐标为(﹣2,0),C点坐标为(0,﹣3);……2分(2)∵y=x2﹣x﹣3,∴对称轴为直线x==1.……3分∵AD在x轴上,点M在抛物线上,∴当△MAD的面积与△CAD的面积相等时,分两种情况:①点M在x轴下方时,根据抛物线的对称性,可知点M与点C关于直线x=1对称,∵C点坐标为(0,﹣3),∴M点坐标为(2,﹣3);……4分②点M在x轴上方时,根据三角形的等面积法,可知M点到x轴的距离等于点C到x轴的距离3.当y=4时,y=x2﹣x﹣3=3,解得x1=1+,x2=1﹣,∴M点坐标为(1+,3)或(1﹣,3).综上所述,所求M点坐标为(2,﹣3)或(1+,3)或(1﹣,3);……5分(3)结论:存在.如图所示,在抛物线上有两个点P满足题意:①若BC∥AP1,此时梯形为ABCP1.由点C关于抛物线对称轴的对称点为B,可知BC∥x轴,则P1与D点重合,∴P1(﹣2,0).∵P1A=6,BC=2,∴P1A≠BC,∴四边形ABCP1为梯形;②若AB∥CP2,此时梯形为ABCP2.……6分∵A点坐标为(4,0),B点坐标为(2,﹣3),∴直线AB的解析式为y=x﹣6,∴可设直线CP2的解析式为y=x+n,将C点坐标(0,﹣3)代入,得b=﹣3,∴直线CP2的解析式为y=x﹣3 .……7分∵点P2在抛物线y=x2﹣x﹣3上,∴y=x2﹣x﹣3=x﹣3,化简得:x2﹣6x=0,解得x1=0(舍去),x2=6,∴点P2横坐标为6,代入直线CP2解析式求得纵坐标为6,∴P2(6,6).……8分∵AB∥CP2,AB≠CP2,∴四边形ABCP2为梯形.综上所述,在抛物线上存在一点P,使得以点A、B、C、P四点为顶点所构成的四边形为梯形;点P的坐标为(﹣2,0)或(6,6).……9分。
2014年数学青年教师解题比赛训练题(七)答案

2014年数学青年教师解题比赛训练题(七)参考答案1、B2、A3、C4、B5、C6、A7、D8、D9、B10、C11、(x+3)(x﹣3)12、1,2,3 13、6,4或5,514、5 15、AC=CD16、3 17、2或0 18、﹣1或419.:解:2cos45°﹣(﹣)﹣1﹣﹣(π﹣)0,=2×﹣(﹣4)﹣2﹣1,=+4﹣2﹣1,=3﹣.20.:解:原式=•=x﹣1,当x=﹣时,原式=﹣﹣1=﹣.21.:解:(1)作出线段AB的垂直平分线;(2)作出角的平分线(2条);它们的交点即为所求作的点C(2个).22.:解:∵在Rt△ADB中,∠BDA=45°,AB=3米,∴DA=3米,在Rt△ADC中,∠CDA=60°,∴tan60°=,∴CA=3.∴BC=CA﹣BA=(3﹣3)米.答:路况显示牌BC是(3﹣3)米.23.:解:(1)点A在y=x﹣2上,∴1=x﹣2,解得x=6,把(6,1)代入得m=6×1=6.∴y=;(2)由图象得,当x>6时,一次函数的值大于反比例函数的值.四、解答题(二):本大题共5小题,共50分,解答时,应写出必要的文字说明、证明过程或演算步骤。
24.:解:(1)列表得:1 2 3 41 ﹣1分1分0分2 1分﹣1分0分3 1分1分﹣0分4 0分0分0分﹣画树状图得:∴P(甲得1分)==(2)不公平.∵P(乙得1分)=∴P(甲得1分)≠P(乙得1分),∴不公平.25.:解:(1)根据条形图得出文学类人数为:70,利用扇形图得出文学类所占百分比为:35%,故本次调查中,一共调查了:70÷35%=200人,故答案为:200;(2)根据科普类所占百分比为:30%,则科普类人数为:n=200×30%=60人,m=200﹣70﹣30﹣60=40人,故m=40,n=60;故答案为:40,60;(3)艺术类读物所在扇形的圆心角是:×360°=72°,故答案为:72;(4)由题意,得(册).答:学校购买其他类读物900册比较合理.26.解:(1)BD=CD.理由如下:∵AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,∵AB=AC,BD=CD,∴∠ADB=90°,∴▱AFBD是矩形.27.:解:(1)∵半径OC垂直于弦AB,∴AE=BE=AB=4,在Rt△OAE中,OA=5,AE=4,∴OE==3,∴EC=OC﹣OE=5﹣3=2,在Rt△AEC中,AE=4,EC=2,∴tan∠BAC===;(2)AD与⊙O相切.理由如下:∵半径OC垂直于弦AB,∵AC弧=BC弧,∴∠AOC=2∠BAC,∵∠DAC=∠BAC,∴∠AOC=∠BAD,∵∠AOC+∠OAE=90°,∴∠BAD+∠OAE=90°,∴OA⊥AD,∴AD为⊙O的切线.28.解:①∵函数的图象与x轴相交于O,∴0=k+1,∴k=﹣1,∴y=x2﹣3x,②假设存在点B,过点B做BD⊥x轴于点D,∵△AOB的面积等于6,∴AO•BD=6,当0=x2﹣3x,x(x﹣3)=0,解得:x=0或3,∴AO=3,∴BD=4即4=x2﹣3x,解得:x=4或x=﹣1(舍去).又∵顶点坐标为:(1.5,﹣2.25).∵2.25<4,∴x轴下方不存在B点,∴点B的坐标为:(4,4);③∵点B的坐标为:(4,4),∴∠BOD=45°,BO==4,当∠POB=90°,∴∠POD=45°,设P点横坐标为:﹣x,则纵坐标为:x2﹣3x,即﹣x=x2﹣3x,解得x=2 或x=0,∴在抛物线上仅存在一点P(2,﹣2).∴OP==2,使∠POB=90°,∴△POB的面积为:PO•BO=×4×2=8.。
2014年惠阳区数学青年教师解题比赛训练题(二)答案

2014年惠阳区数学青年教师解题比赛训练题(二)参考答案一、选择题.每题3分,共5小题,共15分.只有一个正确答案.1.D2.C3.B4.A5.A二、填空题.每题3分,共8题,共24分.6.3.7.48°.8.m(m﹣2).9.3a.10.8×106.11.105.12.1.13.()2013.三、解答题.共10小题,共81分.14.解:原式=1×2﹣﹣3+2×=﹣.15.解:,①+②得:3x=6,解得x=2,将x=2代入②得:2﹣y=1,解得:y=1.∴原方程组的解为16.解:(1)∵点C与点A(﹣2,2)关于原点O对称,∴点C的坐标为(2,﹣2);(2)∵将点A向右平移5个单位得到点D,点D的坐标为(3,2);(3)由图可知:A(﹣2,2),B(﹣3,﹣2),C(2,﹣2),D(3,2),∵在平行四边形ABCD内横、纵坐标均为整数的点有15个,其中横、纵坐标和为零的点有3个,即(﹣1,1),(0,0),(1,﹣1),∴P==.故答案为(2,﹣2);(3,2);17.解:(1)根据题意得:18÷30%=60(人),则九年级(1)班的人数为60人;(2)“一般”的人数为60×15%=9(人),“较差”的人数为60﹣(9+30+18)=3(人),则“较差”所占的度数为360°×=18°;(3)“较差”、“一般”的学生所占的百分比之和为5%+15%=20%,则对安全知识的了解情况为“较差”、“一般”的学生共有1500×20%=300(名).18.解:(1)将A(a,2)代入y=x+1中得:2=a+1,解得:a=1,即A(1,2),将A(1,2)代入反比例解析式中得:k=2,则反比例解析式为y=;(2)将x=2代入反比例解析式得:y==,则点B在反比例图象上.19.解;(1)∵在矩形ABCD中,AB=2DA,DA=2,∴AB=AE=4,∴DE==2,∴EC=CD﹣DE=4﹣2;(2)∵sin∠DEA==,∴∠DEA=30°,∴∠EAB=30°,∴图中阴影部分的面积为:S扇形F AB﹣S△DAE﹣S扇形EAB=﹣×2×2﹣=﹣2.20.解:(1)设购买A种树苗x棵,则购买B种树苗(1000﹣x)棵,由题意,得y=(20+5)x+(30+5)(1000﹣x)=﹣10x+35000;(2)由题意,可得0.90x+0.95(1000﹣x)=925,解得x=500.当x=500时,y=﹣10×500+35000=30000,即绿化村道的总费用需要30000元;(3)由(1)知购买A种树苗x棵,B种树苗(1000﹣x)棵时,总费用y=﹣10x+35000,由题意,得﹣10x+35000≤31000,解得x≥400,所以1000﹣x≤600,故最多可购买B种树苗600棵.21.(1)证明:∵EF垂直平分BC,∴CF=BF,BE=CE,∠BDE=90°,BD=CD,又∵∠ACB=90°,∴EF∥AC,∴BE:AB=DB:BC,∵D为BC中点,∴DB:BC=1:2,∴BE:AB=1:2,∴E为AB中点,即BE=AE,∵CF=AE,∴CF=BE,∴CF=FB=BE=CE,∴四边形BECF是菱形.(2)解:∵四边形BECF是正方形,∴∠CBA=45°,∵∠ACB=90°,∴∠A=45°.22.解:(1)∵y=2x2﹣2,∴当y=0时,2x2﹣2=0,x=±1,∴点A的坐标为(﹣1,0),点B的坐标为(1,0),AB=2,又当x=0时,y=﹣2,∴点C的坐标为(0,﹣2),OC=2,∴S△ABC=AB•OC=×2×2=2;(2)将y=6代入y=2x2﹣2,得2x2﹣2=6,x=±2,∴点M的坐标为(﹣2,6),点N的坐标为(2,6),MN=4.∵平行四边形的面积为8,∴MN边上的高为:8÷4=2,∴P点纵坐标为6±2.①当P点纵坐标为6+2=8时,2x2﹣2=8,x=±,∴点P的坐标为(,8),点N的坐标为(﹣,8);②当P点纵坐标为6﹣2=4时,2x2﹣2=4,x=±,∴点P的坐标为(,4),点N的坐标为(﹣,4);(3)∵点B的坐标为(1,0),点C的坐标为(0,﹣2),∴OB=1,OC=2.∵∠QDB=∠BOC=90°,∴以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似时,分两种情况:①OB与BD边是对应边时,△OBC∽△DBQ,则=,即=,解得DQ=2(m﹣1)=2m﹣2,②OB与QD边是对应边时,△OBC∽△DQB,则=,即=,解得DQ=.综上所述,线段QD的长为2m﹣2或.23.解:探究一:(1)依题意画出图形,如答图1所示:由题意,得∠CFB=60°,FP为角平分线,则∠CFP=30°,∴CF=BC•sin30°=3×=,∴CP=CF•tan∠CFP=×=1.过点A作AG⊥BC于点G,则AG=BC=,∴PG=CG﹣CP=﹣1=.在Rt△APG中,由勾股定理得:AP===.(2)由(1)可知,FC=.如答图2所示,以点A为圆心,以FC=长为半径画弧,与BC交于点P1、P2,则AP1=AP2=.过点A过AG⊥BC于点G,则AG=BC=.在Rt△AGP1中,cos∠P1AG===,∴∠P1AG=30°,∴∠P1AB=45°﹣30°=15°;同理求得,∠P2AG=30°,∠P2AB=45°+30°=75°.∴∠P AB的度数为15°或75°.探究二:△AMN的周长存在有最小值.如答图3所示,连接AD.∵△ABC为等腰直角三角形,点D为斜边BC的中点,∴AD=CD,∠C=∠MAD=45°.∵∠EDF=90°,∠ADC=90°,∴∠MDA=∠NDC.∵在△AMD与△CND中,∴△AMD≌△CND(ASA).∴AM=CN.设AM=x,则CN=x,AN=AC﹣CN=BC﹣CN=﹣x.在Rt△AMN中,由勾股定理得:MN====.△AMN的周长为:AM+AN+MN=+,当x=时,有最小值,最小值为+=.∴△AMN周长的最小值为.。
2014年惠阳区数学青年教师解题比赛训练题(五)答案
四、应用题
22、
解答:
解:∵弓形的跨度AB=3cm,EF为弓形的高,
∴பைடு நூலகம்E⊥AB,
∴AF= AB= cm,
∵ 所在圆O的半径为r,弓形的高EF=1cm,
∴AO=r,OF=r﹣1,
在Rt△AOF中,AO2=AF2+OF2,
即r2=( )2+(r﹣1)2,
③若AB=BD,则点D与点C重合,可知此时点P、点P′、点M均与点C重合,
∴S△ABD=S△ABC= AB•BC= ×4×4=8.
则x=20,21,
共有2种搭建方案:
方案一:甲种板房搭建20间,乙种板房搭建80间,
方案二:甲种板房搭建21间,乙种板房搭建79间.
五、综合题
25、
解答:
解:(1)∵抛物线y=﹣2x2﹣4x=﹣2(x+1)2+2的图象E,将其向右平移两个单位后得到图象F,
∴图象F所表示的抛物线的解析式为y=﹣2(x+1﹣2)2+2,即y=﹣2(x﹣1)2+2;
(2)∵星期日的日访问总量为3万人次,星期日学生日访问总量占日访问总量的百分比为30%,
∴星期日学生日访问总量为:3×30%=0.9(万人次);
(3)某教育网站一周内星期日的日访问总量最大.
24、
解答:
解:设甲种板房搭建x间,则乙种板房搭建(100﹣x)间,根据题意得:
,
解得:20≤x≤21,
x只能取整数,
(2)∵y=﹣2(x﹣1)2+2,
∴顶点C的坐标为(1,2).
当y=0时,﹣2(x﹣1)2+2=0,
解得x=0或2,
2014年惠阳区数学青年教师解题比赛训练题(十九)答案
2014年惠阳区数学青年教师解题比赛训练题(十九)答案一、选择题1.A 2.B 3.C 4.B 5.D 6.C 7.A 8.D 9.B 10.B 二、填空题11.67.8410⨯ 12.3x =- 13.2:5 14.外切 15.3516.30 三、解答题17.解:原式23131=+⨯-+ ···································································· (5分) 3=. ·················································································· (6分) 18.解:由①,得3x >-. ······································································· (2分)由②,得2x ≤. ········································································ (4分) 所以,原不等式组的解集为32x -<≤. ········································· (6分)19.解:已知:线段AB . ········································································ (1分) 求作:等边ABC △. ··············································································· (2分) 作图如下:(注:每段弧各1分,连接线段AC BC 、各1分)····························································· (6分)20············································· (4分)(2)补图如下:························ (6分)四、解答题:21.解:原式221(1)2(2)(2)x x x x x +-+=÷++- ······················································ (4分) 21(2)(2)2(1)x x x x x ++-=++ ·············································································· (6分) ABC (株)21x x -=+. ······························································································ (8分) 当3x =-时,原式325312--==-+. ····························································· (10分) 22.解:(1)42OB OE == ,,246BE ∴=+=. CE x ⊥轴于点E .1tan 2CE ABO BE ∴∠==,3CE ∴=. ························································· (1分)∴点C 的坐标为()23C -,. ······································································· (2分) 设反比例函数的解析式为(0)my m x=≠. 将点C 的坐标代入,得32m=-, ································································ (3分) 6m ∴=-. ···························································································· (4分)∴该反比例函数的解析式为6y x=-.·························································· (5分) (2)4OB = ,(40)B ∴,. ···································································· (6分) 1tan 2OA ABO OB ∠== , 2OA ∴=,(02)A ∴,. ············································································ (7分)设直线AB 的解析式为(0)y kx b k =+≠.将点A B 、的坐标分别代入,得240.b k b =⎧⎨+=⎩, ················································· (8分)解得122.k b ⎧=-⎪⎨⎪=⎩, ························································································ (9分) ∴直线AB 的解析式为122y x =-+. ························································ (10分) 23.解:(1)画树状图如下: ··················· (4分)0 1 30 2 60 3 90 4 120 1 3 0 1 3 0 1 3 0 1 3 2 3 4 1 幸运数 吉祥数 积············································································································ (4分) 由图(表)知,所有等可能的结果有12种,其中积为0的有4种, 所以,积为0的概率为41123P ==. ··························································· (6分) (2)不公平.························································································· (7分) 因为由图(表)知,积为奇数的有4种,积为偶数的有8种.所以,积为奇数的概率为141123P ==,························································ (8分) 积为偶数的概率为282123P ==. ································································ (9分) 因为1233≠,所以,该游戏不公平.游戏规则可修改为:若这两个数的积为0,则小亮赢;积为奇数,则小红赢. ································ (10分) (只要正确即可)24.(1)证明:90ABC DE AC ∠= °,⊥于点F , ABC AFE ∴∠=∠.································· (1分)AC AE EAF CAB =∠=∠ ,, ABC AFE ∴△≌△ ·································· (2分)AB AF ∴=. ········································· (3分)连接AG , ·············································· (4分)AG AG AB AF == ,,Rt Rt ABG AFG ∴△≌△. ······················ (5分)BG FG ∴=. ········································· (6分) (2)解:AD DC DF AC = ,⊥,1122AF AC AE ∴==. ··········································································· (7分) 30E∴∠=°.30FAD E ∴∠=∠=°,············································································ (8分) AF ∴= ························································································· (9分) AB AF ∴= ················································································ (10分) 五、解答题:25.解:(1)设p 与x 的函数关系为(0)p kx b k =+≠,根据题意,得3.954.3.k b k b +=⎧⎨+=⎩,························································································· (1分) D CE B G AF解得0.13.8.k b =⎧⎨=⎩,所以,0.1 3.8p x =+. ························································· (2分)设月销售金额为w 万元,则(0.1 3.8)(502600)w py x x ==+-+. ··················· (3分) 化简,得25709800w x x =-++,所以,25(7)10125w x =--+.当7x =时,w 取得最大值,最大值为10125.答:该品牌电视机在去年7月份销往农村的销售金额最大,最大是10125万元.··· (4分) (2)去年12月份每台的售价为501226002000-⨯+=(元), 去年12月份的销售量为0.112 3.85⨯+=(万台), ······································ (5分) 根据题意,得2000(1%)[5(1 1.5%) 1.5]13%3936m m -⨯-+⨯⨯=. ················· (8分) 令%m t =,原方程可化为27.514 5.30t t -+=.t ∴==. 10.528t ∴≈,2 1.339t ≈(舍去)答:m 的值约为52.8. ············································································ (10分)26.解:(1)由已知,得(30)C ,,(22)D ,, 90ADE CDB BCD ∠=-∠=∠ °,1tan 2tan 212AE AD ADE BCD ∴=∠=⨯∠=⨯= . ∴(01)E ,. ···························································································· (1分) 设过点E D C 、、的抛物线的解析式为2(0)y ax bx c a =++≠. 将点E 的坐标代入,得1c =.将1c =和点D C 、的坐标分别代入,得42129310.a b a b ++=⎧⎨++=⎩,····················································································· (2分) 解这个方程组,得56136a b ⎧=-⎪⎪⎨⎪=⎪⎩故抛物线的解析式为2513166y x x =-++. ·················································· (3分) (2)2EF GO =成立. ············································································ (4分)点M 在该抛物线上,且它的横坐标为65,∴点M 的纵坐标为125. ··········································································· (5分) 设DM 的解析式为1(0)y kx b k =+≠, 将点D M 、的坐标分别代入,得1122612.55k b k b +=⎧⎪⎨+=⎪⎩, 解得1123k b ⎧=-⎪⎨⎪=⎩,. ∴DM 的解析式为132y x =-+. ······························································ (6分) ∴(03)F ,,2EF =. ·············································································· (7分) 过点D 作DK OC ⊥于点K ,则DA DK =.90ADK FDG ∠=∠= °, FDA GDK ∴∠=∠.又90FAD GKD ∠=∠= °, DAF DKG ∴△≌△. 1KG AF ∴==. 1GO ∴=. ···························································································· (8分) 2EF GO ∴=.(3) 点P 在AB 上,(10)G ,,(30)C ,,则设(12)P ,. ∴222(1)2PG t =-+,222(3)2PC t =-+,2GC =.①若PG PC =,则2222(1)2(3)2t t -+=-+,解得2t =.∴(22)P ,,此时点Q 与点P 重合. ∴(22)Q ,. ···························································································· (9分) ②若PG GC =,则22(1)22t 2-+=,解得 1t =,(12)P ∴,,此时GP x ⊥轴. GP 与该抛物线在第一象限内的交点Q 的横坐标为1,∴点Q 的纵坐标为73.∴713Q ⎛⎫⎪⎝⎭,. ························································································· (10分)x③若PC GC =,则222(3)22t -+=,解得3t =,(32)P ∴,,此时2PC GC ==,PCG △是等腰直角三角形. 过点Q 作QH x ⊥轴于点H , 则QH GH =,设QH h =,(1)Q h h ∴+,.2513(1)(1)166h h h ∴-++++=.解得12725h h ==-,(舍去).12755Q ⎛⎫∴ ⎪⎝⎭,.····································· (12分) 综上所述,存在三个满足条件的点Q ,即(22)Q ,或713Q ⎛⎫⎪⎝⎭,或12755Q ⎛⎫⎪⎝⎭,.x。
2014年长沙县初中教师解题比赛试卷(含答案)
长沙县2014年初中数学教师解题比赛试题卷(比赛时间:2014年4月25日上午9∶00-11∶00)本试卷共4页,共三大题25小题,满分150分,考试时间120分钟。
一、选择题(本大题共10小题,每小题4分,满分40分)1、对于实数a 、b ,定义一种运算“⊗”为:a ⊗b =a 2+ab ﹣2,有下列命题: ①1⊗3=2;②方程x ⊗1=0的根为:x 1=﹣2,x 2=1;③不等式组的解集为:﹣1<x <4;④点(51,)在函数y =x ⊗(﹣1)的图象上.其中正确的是: 2、若-1<a <0,则a a a ,,,33一定是: 3、如左下图,直线L 1、L 2、L 3表示三条互相交叉的公路,要建一个货物中转站,要求它到三条公4、如图,在O ⊙上有定点C 和动点P ,位于直径AB 的异侧, 过点C 作CP 的垂线,与PB 的延长线交于点Q ,已知:O ⊙半径为5,tan ∠ABC =3,则CQ 的最大值是:5、设12x x ,是方程0132=++x x 的两个根,则=-2213x x 6、若n 为整数,则能使也为整数的n 的个数有:第3题图 第4题图 正视图 侧视图第7题图8、下列图形中,阴影部分的面积相等的有: 9、已知sin()α+=,那么cos α=锐角的个数最多为:11、我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”,“面线”被这个平面图形截得的线段叫做该图形的“面径”(例如圆的直径就是它的“面径”).已知等边三角形的边长为2,则它的“面径”R 长的取值范围是 .12、如图,四边形ABCD 是一个矩形,C ⊙的半径是2cm , CE ,2cm EF =.则图中阴影部分面积约为 2cm .13、如果关于x 的不等式组22,4,x a x a >-⎧⎨<-⎩有解,并且所有解都是不等式组-6<x ≤5的解,则a 的取值范围是 .14、若正整数n 使得在计算n+(n+1)+(n+2)的过程中,各个数位上均不产生进位的现象,则称n 为“本位数”,例如2和30是 “本位数”,而5和91不是“本位数”。
2014初中数学青年教师解题大赛试题参考答案
2014年安庆市初中数学青年教师解题大赛试题参考答案(2014年12月4日下午1:30—4:00)一、选择题(每题6分,共36分) 1. 已知22466-+-=a ,则62623+++a a a 的值为(C )A.2-B.2C.6D.6-2. 已知c b a ,,满足()ac c a b a b a 223242222+=++-+++-,则c b a +-的值为( D )A. 4B.6C.8D.4或83.小青步行从家出发,匀速向学校走去,同时她哥哥小强骑摩托车从学校出发,匀速向家驶去,二人在途中相遇,小强立即把小青送到学校,再向家里驶去,这样他在途中所用的时间是原来从学校直接驶回家所用时间的2.5倍,那么小强骑摩托车的速度是小青步行速度的 ( B ).A. 2倍B. 3倍C.4倍D. 5倍4. 方程a x =--112的解的个数是4,则a 的取值范围为( B )A.21>a B.10<<a C.1>a D.210<<a 5. 平面上动点),(y x A 满足135=+y x ,)0,4(-B ,)0,4(C ,则一定有( B )A . 10<+AC AB B .10≤+AC AB C . 10>+AC ABD .10≥+AC AB6. 函数f (x )=ax 2+bx +c (a ≠0),对任意的非0实数a 、b 、c 、m 、n 、g 关于x 的方程m [f (x )]2+n f (x )+g =0的解集不可能是( D )A. {1,3} B . {2,4} C . {1,2,3,4} D . {1,2,4,8} 二、填空题(每题8分,共32分)7. 设集合{a3+b ︱1≤a ≤b ≤2}中的最大元素与最小元素分别为M 、m,则M-m的值为5-2√3 。
8. 化简:()()211543143213211++⨯++⨯⨯+⨯⨯+⨯⨯n n n K =n 2+3n/4(n+1)(n+2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年安庆市初中数学青年教师解题大赛试题参考答案(2014年12月4日下午1:30—4:00)一、选择题(每题6分,共36分) 1. 已知22466-+-=a ,则62623+++a a a 的值为(C )A.2-B.2C.6D.6-2. 已知c b a ,,满足()ac c a b a b a 223242222+=++-+++-,则c b a +-的值为( D )A. 4B.6C.8D.4或83.小青步行从家出发,匀速向学校走去,同时她哥哥小强骑摩托车从学校出发,匀速向家驶去,二人在途中相遇,小强立即把小青送到学校,再向家里驶去,这样他在途中所用的时间是原来从学校直接驶回家所用时间的2.5倍,那么小强骑摩托车的速度是小青步行速度的 ( B ).A. 2倍B. 3倍C.4倍D. 5倍4. 方程a x =--112的解的个数是4,则a 的取值范围为( B )A.21>a B.10<<a C.1>a D.210<<a 5. 平面上动点),(y x A 满足135=+y x ,)0,4(-B ,)0,4(C ,则一定有( B )A . 10<+AC AB B .10≤+AC AB C . 10>+AC ABD .10≥+AC AB6. 函数f (x )=ax 2+bx +c (a ≠0),对任意的非0实数a 、b 、c 、m 、n 、g 关于x 的方程m [f (x )]2+n f (x )+g =0的解集不可能是( D )A. {1,3} B . {2,4} C . {1,2,3,4} D . {1,2,4,8} 二、填空题(每题8分,共32分)7. 设集合{a3+b ︱1≤a ≤b ≤2}中的最大元素与最小元素分别为M 、m,则M-m的值为5-2√3 。
8. 化简:()()211543143213211++⨯++⨯⨯+⨯⨯+⨯⨯n n n =n 2+3n/4(n+1)(n+2)。
9. 在ABC ∆中,4=AB ,2=BCAC则ABC ∆的面积的最大值为 16/3 . 10. 袋内有8个白球和2个红球,每次从中随机取出一个球,然后放进1个白球,则第4县市学校学姓名 姓次恰好取完所有红球的概率为 434/10000 .三、解答题(共82分)11.(本题12分)如图,点P是正方形ABCD边AB上一点(不与点A B,重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE DF,.(1)求证:ADP EPB∠=∠;(2)求CBE∠的度数;(3)当APAB的值等于多少时,PFD BFP△∽△?并说明理由.证明: (1)在正方形ABCD中,∠A=90°,∴∠ADP+∠APD=90°∵∠DPE=90°∴∠EPB+∠APD=90°∴A D P E P B∠=∠;(2)作EG⊥AB交AB的延长线于G,∴∠PGE=∠A=90°又∵ADP EPB∠=∠,DP=PE∴⊿ADP≌⊿PGE∴AD=PG=AB,AP=GE∴AB-PB=PG-PB 即AP=BG∴BG=GE∴∠EBG=∠BEG=45°∴∠CBE=45°(3)当APAB的值等于1/2时,PFD BFP△∽△证明:∵∠A=∠PBF=90°、ADP EPB∠=∠∴⊿ADP∽⊿BPF∴DP/PF=AP/BF当APAB的值等于1/2时,AP=PB∴DP/PF=PB/BF∴DP/PB=PF/BF∵∠DPE=∠PBF=90°∴PFD BFP△∽△12.(本题15分)请用一个长方形纸片折出一个30°的角(不借助任何工具)写出你的作法,并说明理由.A'GFE CDABH作法: 如图,将长方形纸片ABCD 沿着一组对边中点对折得折痕EF再将∠A 沿着过点B 的直线折叠使点A 落在折痕EF 上的点A ’处得折痕BG ,,则∠ABG=∠GBA ’=∠A ’BC=30°证明 : 延长GA ’交BC 于H,由作图知: AD ∥EF ∥BC AE=EB∠BA ’G= =90°=∠BA ’H ∴A ’G=A ’H 又∵BA ’=BA ’ ∴⊿ADP ≌⊿PGE ∴∠GBA ’=∠HBA ’由折纸知∠ABG=∠GBA ’,∠ABC =90°∴ ∠ABG=∠GBA ’=∠A ’BC=30° 13..(本题共20分)凸四边形ABCD 内接于⊙O ,其中AC 为⊙O 直径,AB=BC ,已知BD=10.求:四边形ABCD 的面积.解:方法1 记AC 和BD 的交点为E,∵AC 为⊙O 直径 ∴∠ABC=∠ADC=90° ∵AB=BC∴∠BAC=∠ACB=∠DAC=∠BDC= 45°E又∵∠ABE=∠DBA ∠CDB=∠CAD ∴⊿BAE ∽⊿BDA ⊿ADE ∽⊿BDC∴AB/BD=BE/AB AD/BD=DE/DC ∴AB 2=BD ×BE AD ×DC=BD ×DE∴AB 2+ AD ×DC= BD ×BE+ BD ×DE=BD(BE+DE)=BD 2=102=100∴S 四边形ABCD =S ⊿ABC + S ⊿ADC =1/2AB ×BC+1/2 AD ×DC=1/2(AB 2+ AD ×DC)=50 方法2: 设圆的半径为R,则AC=2R,AB=BC=√2R 运用托勒密定理可得AB ×CD+BC ×AD=AC ×BD即√2R ×CD+√2R ×AD=2R ×10从而得AD+CD=10√2S 四边形ABCD =S ⊿BAD + S ⊿BCD =1/2BD ×AD ×Sin45°+1/2BD ×CD ×Sin45° =1/2BD ×Sin45°(AD+CD) =1/2×10×√2/2×10√2=50 方法3: 可分别过点A 、C 作BD 上的垂线段AE 、CF用⊿ABE ≌⊿BCF 可以得到AE+CF=BD=10方法4:过点A 作BD 的垂线垂足为E,交圆于F,连接CF,用圆周角,弧,弦得关系可证AF=BD=10 S 四边形ABCD =1/2BD ×AF=50方法5: 在4得到 AD+CD=10√2后,将他平方得AD 2+CD 2+2AD ×CD=200 由勾股定理 AD 2+CD 2=AC 2=2AB 22AB 2+2AD ×CD=200 S 四边形ABCD =S ⊿ABC + S ⊿ADC =1/2(AB 2+ AD ×DC)=5014.(本题20分)如图,抛物线y=ax 2+bx -1经过A (-1,0)、B (2,0)两点,交y 轴于点C .点P 为抛物线上的一个动点,过点P 作x 轴的垂线交直线BC 于点D ,交x 轴于点E .(1)请直接写出抛物线表达式和直线BC 的表达式.(2)如图1,当点P 的横坐标为 时,求证:△OBD ∽△ABC . (3)如图2,若点P 在第四象限内,当OE =2PE 时,求△POD 的面积. (4)当以点O、C、D为顶点的三角形是等腰三角形时,请直接写出动点P的坐标.32x PABCO PxyxyAB COD E图1 图2 备用图yA B CO DE解:(1)由待定系数法得抛物线表达式为y=1/2x 2-1/2x -1 直线BC 的表达式为y=1/2x -1证明:(2)∵点P 的横坐标为 ,即x= 时y P =-10/9 y D =-2/3 ∵ED= y D -y P =2/3=OE ∴∠EOD=∠EDO= 45°又∵OA=OC=1∴∠OAC=∠OCA= 45° ∴∠OAC=∠EOD 又∵∠OBD=∠ABC ∴△OBD ∽△ABC .(3) OE =2PE OE=x PE=-y=-1/2x 2+1/2x +1)2(-1/2x 2+1/2x +1)= x解得x 1=-√2(舍去) x 2=√2即OE= √2 PE=√2/2, DE=y D =√2/2-1 PD=PE-DE=1s △POD =1/2PD ×OE=√2/2(4) 点P 的坐标为:(2√5/5, 3/5-√5/5)或(-2√5/5,-3/5+√5/5).或(4/5,-37/25) 或(1,-1)15.(本题15分)证明:不存在整数,,y x 使得1222322=-+y xy x 成立。
证明:假设存在整数,,y x 使得1222322=-+y xy x 成立,则关于x 得一元二次方程x 2+3xy-(2y 2+122)=0在y 是整数时有整数解, 于是⊿=(3y )2+4 (2y 2+122)=17y 2+488是完全平方数, 设m 2=17y 2+488=17(y 2+28)+12m 2-12=17(y 2+28) 故m 2-12能被17整除, 显然,整数m 不能被17整除,再设整数m=17n+p,其中n 为任意整数,|P|=1、2、3、 (8)m 2-12=(17n+p )2-12=17(17n 2+2nP )+p 2-12 其中17(17n 2+2nP )能被17整除 而当|P|=1、2、3、…8时,p 2-12=|p|2-12=-11、-8、-3、4、13、24、37、52都不能被17整除,所以m 2-12=(17n+p )2-12=17(17n 2+2nP )+p 2-12一定不能被17整除, 这就与前面所说m 2-12能被17整除相矛盾,所以假设“存在整数,,y x 使得1222322=-+y xy x 成立”是错误的; 所以不存在整数,,y x 使得1222322=-+y xy x 成立。
初中组13题和高中组的一题,有些解题方法很相似附:高中组中平面几何证明3232方法1:用相似三角形 记AB 、PC 得交点为E 设正三角形边长为a ,易证:⊿PAE ∽⊿PCB ⊿ACE ∽⊿PCA∴PA ×PB=PE ×PC AC 2=CE ×PC∴PA ×PB+ AC 2 = PE ×PC+ CE ×PC=PC(PE+CE)=PC 2∴PC 2- PA ×PB=AC 2=a 2=3R 2 即PC 2-PA ×PB 为定值3R 2 方法2:用特勒密定理证PC=PA+PB证明:设正三角形边长为a ,由特勒密定理得:PC ×AB=AP ×BC+BP ×AC即aPC=aAP+aBP 所以PC=PA+PB所以PC 2-PA ×PB=(PA+PB)2- PA ×PB= PA 2+PB 2+PA ×PB=a 2=3R 2即PC 2-PA ×PB 为定值3R 2 方法3:用余弦定理证PC=PA+PB证明 :设正三角形边长为a,在△APC 、△BPC 、△APB 中, ∠APC=∠BPC=60° ∠BPA=120° 根据余弦定理得 :a 2=PA 2+PC 2-2PA ×PC ×COS60°= PA 2+PC 2-PA ×PC (1) a 2=PB 2+PC 2-2PB ×PC ×COS60°= PB 2+PC 2-PB ×PC (2) a 2=PA 2+PB 2-2PA ×PB ×COS120°= PA 2+PB 2+PA ×PB (3)由(1)-(2)得:(PA 2+PC 2-PA ×PC )-( PB 2+PC 2-PB ×PC )=0 整理得:PA ×PC-PB ×PC=PA 2-PB 2=(PA+PB)(PA-PB) 所以 PC=PA+PB所以PC 2-PA ×PB=(PA+PB)2- PA ×PB= PA 2+PB 2+PA ×PB=a 2=3R 2 即PC 2-PA ×PB 为定值3R 2方法4:构造全等三角形(如图做辅助线可通过全等证明PC=PA+PB )CCABBAPPE。
