八年级数学第8讲.四边形中的动点问题.尖子班.教师版.docx
第8讲四边形动点问题

(4)如图,矩形纸片 ABCD 中, AB 26 厘米, BC 18.5 厘米,点 E 在 AD 上,且 AE=6 厘
米,点 P 是 AB 边上一动点.按如下操作: 步骤一,折叠纸片,使点 P 与点 E 重合,展开纸片得折痕 MN(如图①);
步骤二,过点 P 作 PT AB ,交 MN 所在的直线于点 Q,连结 QE(如图②).
Page 1 of 9
模块一 翻折与动点
【例 1】(1)如图,四边形 ABCD 是边长为 9 的正方形纸片, B' 为 CD 边上的点, B'C 3 . 将纸片沿某直线折叠,使点 B 落在点 B' 处,点 A 的对应点为 A' ,折痕分别与 AD,BC 边交于
点 M,N. 求:(1)求 BN 的长;(2)求四边形 ABNM 的面积
将正方形折叠,使点 A 与点 E 重合,折痕为 MN ,求 ANE 的面积.
DM
C
E
A
N
B
(2) 已知:如图,梯形 ABCD 中, AD ∥ BC , B 90 , AD AB 4 , BC 7 ,点 E
在 BC 边上,将△CDE 沿 DE 折叠,点 C 恰好落在 AB 边上的点 C ' 处.
图①
图②
图③
①无论点 P 在 AB 边上任何位置,都有 PQ
QE(填“>”、“=”、“<”);
②如图③所示,将矩形纸片 ABCD 放在直角坐标系中,按上述步骤一、二进行操作:
(i)当点 P 在 A 点时,PT 与 MN 交于点 Q1 , Q1 点的坐标是(
,
);
(ii)当 PA=6 厘米时,PT 与 MN 交于点 Q2 , Q2 点的坐标是(
初二数学-特殊四边形中的动点问题(学生版)word版本

初二数学-特殊四边形中的动点问题(学生版)特殊四边形中的动点问题及解题方法1、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向D以1cm/s的速度运动;动点Q从点C开始沿CB边向B以3cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.2、(1)当t为何值时,四边形PQCD为平行四边形?3、(2)当t为何值时,四边形PQCD为等腰梯形?4、(3)当t为何值时,四边形PQCD为直角梯形?5、如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.6、(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;7、(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.8、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.9、(1)求NC,MC的长(用t的代数式表示);(2)当t为何值时,四边形PCDQ构成平行四边形;10、(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;11、(4)探究:t为何值时,△PMC为等腰三角形.4、直线y=- 34x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O⇒B⇒A运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;(3)当S= 485时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.5.已知:如图,在直角梯形COAB 中,OC AB ∥,以O 为原点建立平面直角坐标系,A B C ,,三点的坐标分别为(80)(810)(04)A B C ,,,,,,点D 为线段BC 的中点,动点P 从点O 出发,以每秒1个单位的速度,沿折线OABD 的路线移动,移动的时间为t 秒.(1)求直线BC 的解析式;(2)若动点P 在线段OA 上移动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的27? (3)动点P 从点O 出发,沿折线OABD 的路线移动过程中,设OPD △的面积为S ,请直接写出S 与t 的函数关系式,并指出自变量t 的取值范围;6.如图,已知中,厘米,厘米,点为的中点.(1)如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,与是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使与全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿三边运动,求经过多长时间点P 与点Q 第一次在的哪条边上相遇?ABC △10AB AC ==8BC =D AB BPD △CQP △BPD △CQP △ABC △ABC △四边形中的动点问题课后作业1. 如图,已知AD 与BC 相交于E ,∠1=∠2=∠3,BD =CD ,∠ADB =90°,CH ⊥AB 于H ,CH 交AD 于F.(1)求证:CD ∥AB ;(2)求证:△BDE ≌△ACE ;(3)若O 为AB 中点,求证:OF=12BE.2、如图1―4―2l ,在边长为a 的菱形ABCD 中,∠DAB =60°,E 是异于A 、D 两点的动点,F 是CD 上的动点,满足A E +CF=a ,说明:不论E 、F 怎样移动,三角形BEF 总是正三角形.3、在平行四边形中,为的中点,连接并延长交的延长线于点.(1)求证:;(2)当与满足什么数量关系时, 四边形是矩形,并说明理由.4、如图l -4-80,已知正方形ABCD 的对角线AC 、BD 相交于点O ,E 是AC 上一点,过点A 作AG ⊥EB ,垂足为G ,AG 交BD 于F ,则OE=OF .(1)请证明0E=OF(2)解答(1)题后,某同学产生了如下猜测:对上述命题,若点E 在AC 的延长线上,AG ⊥EB ,AG 交 EB 的延长线于 G ,AG 的延长线交DB 的延长线于点F ,其他条件不变,则仍有OE=OF .问:猜测所得结论是否成立?若成立,请给出证明;若不成立,请说明理由.ABCD E BC AE DC F CF AB BC AF ABFC F EDCB AE5、如图,在梯形ABCD 中,3545AD BC AD DC AB B ====︒∥,,,.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒.(1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探究:t 为何值时,MNC △6. 如图所示,有四个动点P 、Q 、E 、F 分别从正方形ABCD 的四个顶点出发,沿着AB 、BC 、CD 、DA 以同样的速度向B 、C 、D 、A 各点移动。
(完整版)初二动点问题(含答案)

动态问题一、所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想 数形结合思想 转化思想类型:1。
利用图形想到三角形全等,相似及三角函数2.分析题目,了解有几个动点,动点的路程,速度(动点怎么动)3.结合图形和题目,得出已知或能间接求出的数据4。
分情况讨论,把每种可能情况列出来,不要漏5.动点一般在中考都是压轴题,步骤不重要,重要的是思路6。
动点类题目一般都有好几问,前一问大都是后一问的提示,就像几何探究类题一样,如果后面的题难了,可以反过去看看前面问题的结论二、例题:1、如图1,梯形ABCD中,AD∥ BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2 cm/秒的速度移动,如果P,Q分别从A,C同时出发,设移动时间为t秒。
当t= 时,四边形是平行四边形;当t= 时,四边形是等腰梯形.2、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1,N为对角线AC上任意一点,则DN+MN的最小值为.的长为 ;的长为 ;4、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD—BE;(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.5、数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BCEFCF于点F,求证:AE=EF.AB的中点M,连接ME,则AM=EC在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点"改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.ACBAED图1NMA BCDEMN图2ACBEDNM图36、如图, 射线MB上,MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB方向以1个单位/秒的速度移动,设P的运动时间为t.求(1)△ PAB为等腰三角形的t值;(2)△ PAB为直角三角形的t值;(3) 若AB=5且∠ABM=45 °,其他条件不变,直接写出△ PAB为直角三角形的t值(1)如果点P在线段BC上以3cm/s的速度由B点向CCA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等,经过1②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能(2)若点Q以②中的运动速度从点C来的运动速度从点B边运动,求经过多长时间点P与点Q第一次哪条边上相遇?A DFC GEB图1A DFC GEB图3A DFC GEB图2。
四边形中的动点问题(带答案)

四边形中的动点问题(带答案)四边形中的动点问题1、如图,把矩形ABCD沿 EF翻折,点B恰好落在AD边的B'处,若AE= 2, DE= 6,Z EFB= 60°, 则矩形ABCD勺面积是 _____________________2、如图,在四边形ABCD中对角线ACL BD 垂足为0,点E, F, G, H分别为边AD AB, BC CD 的中点•若AC= 8, BD= 6,则四边形EFGH的面积为3、如图,正方形ABCD勺边长为4,点P在DC 边上,且DP= 1,点Q是AC上一动点,则D® PQ 的最小值为 _____________________4、如图,在Rt△ ABC中,/ B= 90°,AC= 60 cm Z A= 60°,点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D, E 运动的时间是t s(0 < t < 15) •过点D作DF 丄BC于点F,连接DE EF.(1)求证:AE= DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)当t为何值时,△ DEF为直角三角形?请说明理由5、如图,在等边三角形ABC中,BC=6cm射线AG// BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t. (1)连接EF当EF经过AC边的中点D时,(1)求证:△ ADE^A CDF:6、在菱形ABCD中,/ B=60°,点E在射线BC上运动,/ EAF=60,点F在射线CD上(1)当点E在线段BC上时(如图1)( 1)求证:EC+CF=A; (2) 当点E在BC的延长线上时(如图2),线段EC CFAB有怎样的相等关系?写出你的猜想,不需证明图1 027、如图,在菱形ABC[中, AB=2 / DAB=60 , 点E 是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N 连接MD AN(1)求证:四边形AMDI是平行四边形;(2)填空:①当AM的值为时,四边形AMD是矩形;②当AM的值为时,四边形AMD是菱形.D8 如图,△ ABC中,点0是边AC上一个动点,过0作直线MN BC 设MN交/ BCA的平分线于点E, 交/ BCA 的外角平分线于点F.(1)探究:线段0E与OF的数量关系并加以证明;(2)当点0运动到何处,且△ ABC满足什么条件时,四边形AECF是正方形?(3)当点0在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明,若不是,则说明理由.9、如图,已知菱形ABC[中, / ABC=60 , AB=8 过线段BD上的一个动点P (不与B、D重合)分别向直线AB AD作垂线,垂足分别为E、F.(1)BD的长是______ ;(2)连接PC当PE+PF+P(取得最小值时,此时PB的长是_______10、如图,/ MON=9°,矩形ABCD勺顶点A B 分别在边OM ON上,当B在边ON上运动时,A随之在OMk运动,矩形ABCD勺形状保持不变,其中AB=2 BC=1运动过程中,点D到点O的最大距离为 __________________ .11、如图,已知矩形ABCD AD=4 CD=10 P是AB上一动点,M N E分别是PD PC CD的中点.(1)求证:四边形PMEI是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN 是菱形;(3)四边形PMEf有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.12、如图,在平行四边形ABCD中,对角线BD=12cm AC=16cm AC BD相交于点0,若E, F 是AC上两动点,分别从A, C两点以相同的速度向C、A 运动,其速度为0.5cm/s。
四边形中的动态问题(动点)

四边形中的动态问题图形中的点、线的运动,构成了数学中的一个新问题——动态几何。
它通常分为三种类型:动点问题、动线问题、动形问题。
在解这类题时,要充分发挥空间想象的能力,往往不要被“动”所迷惑,而是要在“动”中求“静”,化“动”为“静”,抓住它运动中的某一瞬间,寻找确定的关系式,就能找到解决问题的途径。
例1、Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上。
令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动,直到C点与N点重合为止。
设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,求y与x之间的函数关系式?例练、菱形OABC的边长为4cm,∠AOC=600,动点P从O出发,以每秒1cm的速度沿O-A-B路线运动,点P出发2秒后,动点Q从O出发,在OA上以每秒1cm的速度运动,在AB上以每秒2cm的速度沿O-A--B运动,过P、Q两点分别作对角线AC的平行线,设P点运动的时间为x秒,这两条平行线在菱形上截出的图形的周长为ycm,问当x为多少时,周长y可能为一个定值,定值为多少?四边形动点问题(一)1.(1)如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?证明你的结论.2.已知等腰△ABC中,AB=AC,AD平分∠BAC交BC于D点,在线段AD上任取一点P(A点除外),过P点作EF∥AB,分别交AC,BC于E,F点,作PM∥AC,交AB于M点,连接ME.(1)求证:四边形AEPM为菱形;(2)当P点在何处时,菱形AEPM的面积为四边形EFBM面积的一半?3. 如图,在梯形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=,∠C=45°,点P是BC边上一动点,设PB的长为x.(1)当x的值为时,以点P、A、D、E为顶点的四边形为直角梯形;(2)当x的值为时,以点P、A、D、E为顶点的四边形为平行四边形;(3)点P在BC边上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.4. 如图,在等腰梯形ABCD中,AD∥BC,BC=4AD=,∠B=45°.直角三角板含45°角的顶点E在边BC上移动,一直角边始终经过点A,斜边与CD交于点F.若△ABE为等腰三角形,则CF的长等于.5.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M从点A开始,沿边AD向点D运动,速度为1cm/s;点N从点C开始,沿边CB向点B运动,速度为2cm/s、点M、N分别从点A、C出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒.(1)当t=时,四边形MNCD是平行四边形.(2)当t=时,四边形MNCD是等腰梯形6.如图,在ΔABC中,D是BC的中点,BC=10㎝,AD=7㎝,从点A沿着A→D的方向运动,速度是每秒2㎝,连结CE,BE,过点B作BF∥CE,交射线AD于点F,设运动时间为t秒(0<t<3.5)(1)求证:ΔBDF≌ΔCDE(2)当t为何值时,四边形BFCE是矩形,说明理由(3)若四边形BFCE是矩形,当AB和CA满足什么条件时,四边形BFCE是正方形。
四边形中的动点问题(带答案)
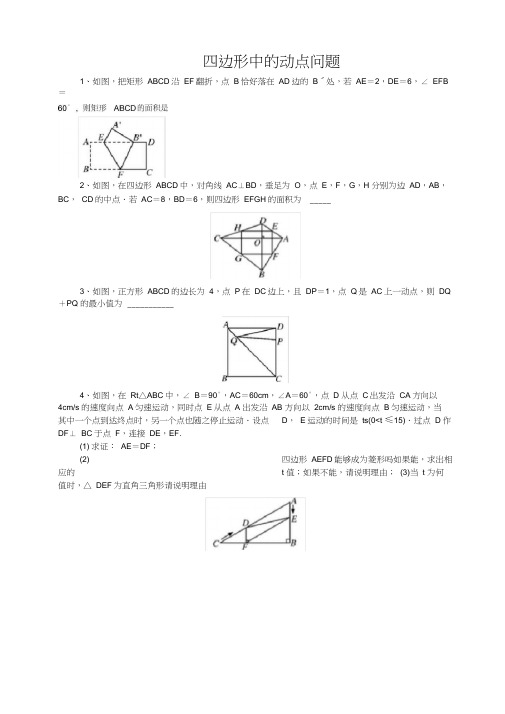
四边形中的动点问题1、如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠ EFB =2、如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H 分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH的面积为 _____3、如图,正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ +PQ 的最小值为___________4、如图,在Rt△ABC中,∠ B=90°,AC=60cm,∠A=60°,点 D 从点C出发沿CA方向以4cm/s 的速度向点A匀速运动,同时点E从点 A 出发沿AB 方向以2cm/s 的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0<t ≤15).过点 D 作DF⊥ BC于点F,连接DE,EF.(1) 求证:AE=DF;(2) 四边形AEFD能够成为菱形吗如果能,求出相应的t 值;如果不能,请说明理由;(3)当t 为何值时,△ DEF为直角三角形请说明理由5、如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点 A 出发沿射线AG以1cm/s 的速度运动,同时点 F 从点 B 出发沿射线BC以2cm/s 的速度运动,设运动时间为t.(1)连接EF,当EF经过AC边的中点 D 时,(1)求证:△ ADE≌△ CDF;:(2)当t 为____ s 时,四边形ACFE是菱形;6、在菱形ABCD中,∠ B=60°,点E在射线BC上运动,∠ EAF=60°,点 F 在射线CD上(1)当点E在线段BC上时(如图1),(1)求证:EC+CF=AB;(2)当点 E 在BC的延长线上时(如图2),线段EC、CF、AB 有怎样的相等关系写出你的猜想,不需证明7、如图,在菱形ABCD中,AB=2,∠ DAB=60°,点E是AD边的中点.点M 是AB边上一动点不与点 A 重合),延长ME交射线CD于点N,连接MD、AN.(1)求证:四边形AMDN 是平行四边形;(2)填空:①当AM 的值为____ 时,四边形AMDN 是矩形;②当AM 的值为____ 时,四边形AMDN 是菱形.8、如图,△ ABC中,点O 是边AC上一个动点,过O 作直线MN ∥BC,设MN 交∠ BCA的平分线于点E,交∠ BCA 的外角平分线于点F.(1)探究:线段OE与OF 的数量关系并加以证明;(2)当点O 运动到何处,且△ ABC满足什么条件时,四边形AECF是正方形(3)当点O 在边AC上运动时,四边形BCFE会是菱形吗若是,请证明,若不是,则说明理由.9、如图,已知菱形ABCD中,∠ ABC=60°,AB=8,过线段BD上的一个动点P(不与B、D 重合)分别向直线AB、AD 作垂线,垂足分别为E、F.(1)BD的长是___ ;(2)连接PC,当PE+PF+PC取得最小值时,此时PB 的长是__10、如图,∠ MON=90°,矩形ABCD的顶点A、B分别在边OM,ON 上,当B在边ON 上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O 的最大距离为_____ .11、如图,已知矩形ABCD,AD=4,CD=10,P 是AB上一动点,M、N、E分别是PD、PC、CD的中点.(1)求证:四边形PMEN 是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN 是菱形;(3)四边形PMEN有可能是矩形吗若有可能,求出AP 的长;若不可能,请说明理由.12、如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F 是AC上两动点,分别从A,C两点以相同的速度向C、A 运动,其速度为/s。
初二数学特殊四边形中地动点问题(教师版)
适用标准文案特别四边形中的动点问题及解题方法1 、如图,在直角梯形ABCD中,AD∥BC,∠ B=90°,AD=24cm,AB=8cm,BC=26cm,动点P 从 A 开始沿 AD边向 D 以 1cm/s的速度运动;动点Q 从点 C 开始沿CB 边向 B 以 3cm/s的速度运动.P 、 Q 分别从点 A 、 C 同时出发,当此中一点抵达端点时,此外一点也随之停止运动,设运动时间为ts .〔 1 〕当t 为什么值时,四边形PQCD为平行四边形?〔 2 〕当t 为什么值时,四边形PQCD为等腰梯形?〔 3 〕当t 为什么值时,四边形PQCD为直角梯形?剖析:〔 1 〕四边形PQCD为平行四边形时PD=CQ.〔 2 〕四边形PQCD为等腰梯形时QC-PD=2CE.(3 〕四边形 PQCD 为直角梯形时QC-PD=EC .全部的关系式都可用含有t 的方程来表示,即本题只需解三个方程即可.解答:解:〔 1 〕∵四边形 PQCD 平行为四边形∴PD=CQ∴24-t=3t解得: t=6即当t=6时,四边形PQCD平行为四边形.文档大全适用标准文案(2〕过 D 作 DE⊥BC 于 E那么四边形ABED为矩形∴BE=AD=24cm∴EC=BC-BE=2cm∵四边形PQCD为等腰梯形∴QC-PD=2CE即 3t- 〔 24-t 〕 =4解得: t=7 〔 s〕即当t=7 〔 s〕时,四边形PQCD为等腰梯形.(3 〕由题意知: QC-PD=EC 时,四边形PQCD为直角梯形即3t- 〔 24-t 〕 =2解得:〔s〕即当〔s〕时,四边形PQCD为直角梯形.评论:本题主要考察了平行四边形、等腰梯形,直角梯形的判断,难易程度适中.2 、如图,△ ABC中,点O 为 AC 边上的一个动点,过点O 作直线MN ∥BC ,设MN交∠BCA的外角均分线CF 于点F,交∠ ACB 内角均分线CE 于 E.文档大全适用标准文案(1 〕试说明 EO=FO ;〔 2〕当点 O 运动到哪处时,四边形AECF 是矩形并证明你的结论;〔 3〕假定 AC 边上存在点O ,使四边形AECF 是正方形,猜想△ ABC 的形状并证明你的结论.剖析:〔 1 〕依据 CE 均分∠ ACB ,MN ∥BC ,找到相等的角,即∠ OEC=∠ECB,再依据等边平等角得OE=OC,同理OC=OF,可得EO=FO.(2 〕利用矩形的判断解答,即有一个内角是直角的平行四边形是矩形.(3 〕利用条件及正方形的性质解答.解答:解:〔 1 〕∵ CE 均分∠ ACB ,∴∠ACE= ∠BCE ,∵MN ∥BC ,∴∠OEC= ∠ECB ,∴∠OEC= ∠OCE ,∴OE=OC,同理, OC=OF,∴OE=OF.〔 2 〕当点O 运动到AC 中点处时,四边形AECF 是矩形.文档大全适用标准文案如图AO=CO,EO=FO,∴四边形AECF 为平行四边形,∵CE 均分∠ ACB ,∴∠ACE=∠ACB,同理,∠ ACF=∠ACG,∴∠ECF= ∠ACE+ ∠ACF=〔∠ACB+∠ACG〕=×180°=90°,∴四边形AECF 是矩形.(3 〕△ABC 是直角三角形∵四边形 AECF 是正方形,∴AC ⊥ EN ,故∠ AOM=90°,∵MN ∥BC ,∴∠BCA= ∠AOM,∴∠BCA=90°,∴△ABC是直角三角形.评论:本题主要考察利用平行线的性质“等角平等边〞证明出结论〔 1 〕,再利用结论〔 1 〕和矩形的判断证明结论〔 2 〕,再对〔 3 〕进行判断.解答时不单要注意用到前一问题的结论,更要注意前一问题为下一问题供给思路,有相像的思虑方法.是矩形的判断和正方形的性质等的综合运用.3 、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=3,BC=4,动点P 从 B 点出发,沿线段BC 向点 C 作匀速运动;动点Q 从点 D 出发,沿线段DA 向点 A 作匀速运动.过Q 点垂直于AD 的射线交AC 于点M ,交 BC 于点N . P、 Q 两点同时出发,速度都为每秒 1 个单位长度.当Q 点运动到 A 点, P 、文档大全适用标准文案Q 两点同时停止运动.设点Q 运动的时间为t 秒.〔 1 〕求NC , MC的长〔用t 的代数式表示〕;〔 2 〕当t 为什么值时,四边形PCDQ组成平行四边形;〔 3 〕能否存在某一时辰,使射线QN恰巧将△ ABC的面积和周长同时均分?假定存在,求出此时t 的值;假定不存在,请说明原因;〔 4 〕研究:t 为什么值时,△PMC为等腰三角形.剖析:〔 1 〕依照题意易知四边形ABNQ是矩形∴ NC=BC-BN=BC-AQ=BC-AD+DQ,BC、AD,DQ就是t,即解;∵AB ∥QN ,∴△CMN ∽△CAB ,∴CM : CA=CN:CB,〔2〕CB、CN,依据勾股定理可求CA=5,即可表示CM ;四边形PCDQ组成平行四边形就是PC=DQ,列方程4-t=t即解;〔 3 〕可先依据QN均分△ ABC的周长,得出MN+NC=AM+BN+AB,据此来求出t 的值.而后依据得出的t 的值,求出△ MNC的面积,即可判断出△MNC的面积能否为△ABC面积的一半,由此可得出能否存在切合条件的t 值.(4 〕因为等腰三角形的两腰不确立,所以分三种状况进行议论:①当 MP=MC 时,那么 PC=2NC ,据此可求出 t 的值.②当 CM=CP时,可依据CM和 CP 的表达式以及题设的等量关系来求出t 的值.③当 MP=PC时,在直角三角形MNP 中,先用t 表示出三边的长,而后依据勾股定理即可得出t 的值.综上所述可得出切合条件的t的值.解答 :文档大全适用标准文案解:〔 1 〕∵ AQ=3-t∴CN=4-〔3-t〕=1+t在 Rt △ABC 中, AC2=AB2+BC2=32+42∴AC=5在 Rt △MNC中,cos∠NCM==,CM=.(2 〕因为四边形 PCDQ 组成平行四边形∴PC=QD ,即 4-t=t解得t=2 .〔 3 〕假如射线QN将△ABC的周长均分,那么有:MN+NC=AM+BN+AB即:〔 1+t 〕 +1+t=〔3+4+5〕解得: t=〔5 分〕而 MN=NC=〔1+t〕∴S△MNC=〔 1+t〕 2=〔 1+t〕 2当 t=时,S△MNC=〔1+t〕2=≠×4×3∴不存在某一时辰t ,使射线QN 恰巧将△ ABC 的面积和周长同时均分.文档大全适用标准文案(4 〕①当 MP=MC 时〔如图 1 〕那么有: NP=NC即 PC=2NC ∴4-t=2 〔 1+t 〕解得: t=②当CM=CP时〔如图 2 〕那么有:(1+t 〕 =4-t解得: t=③当PM=PC时〔如图 3 〕那么有:在 Rt △MNP 中, PM2=MN2+PN2而 MN=NC=〔1+t〕PN=NC-PC=〔1+t〕-〔4-t〕=2t-3∴[〔1+t〕]2+〔2t-3〕2=〔4-t〕2解得: t1=,t2=-1〔舍去〕∴当 t=,t=,t=时,△ PMC为等腰三角形评论:本题繁琐,难度中等,考察平行四边形性质及等腰三角形性质.考察学生疏类议论和数形联合的数学思想方法.4 、直线y=- 34x+6与坐标轴分别交于 A 、 B 两点,动点P 、 Q 同时从O 点出发,同时抵达 A 点,运动停止.点Q 沿线段OA 运动,速度为每秒 1 个单位长度,点P 沿路线O ? B? A 运动.〔 1 〕直接写出 A 、 B 两点的坐标;〔 2 〕设点Q 的运动时间为t 〔秒〕,△OPQ的面积为S,求出S 与 t 之间的函数关系式;〔 3 〕当S= 485时,求出点P 的坐标,并直接写出以点O 、 P 、 Q 为极点的平行四边形的第四个极点M 的坐标.文档大全适用标准文案剖析:〔 1 〕分别令y=0 , x=0 ,即可求出 A 、 B 的坐标;〔 2 〕〕因为OA=8,OB=6,利用勾股定理可得AB=10,从而可求出点Q 由 O 到 A 的时间是8 秒,点P 的速度是 2,从而可求出,当 P 在线段OB 上运动〔或 0 ≤t ≤3 〕时, OQ=t,OP=2t,S=t2,当P在线段BA 上运动〔或 3 < t ≤8 〕时, OQ=t,AP=6+10-2t=16-2t,作PD ⊥ OA 于点 D ,由相像三角形的性质,得PD=48-6t5,利用S= 12OQ×PD,即可求出答案;〔 3 〕令S= 485 ,求出t 的值,从而求出OD 、 PD ,即可求出P 的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M 的坐标.解答:解:〔 1 〕 y=0 , x=0 ,求得 A 〔 8 , 0 〕 B 〔 0 , 6〕,(2 〕∵OA=8 , OB=6 ,∴AB=10 .∵点Q由O到A的时间是81=8 〔秒〕,∴点 P 的速度是6+108=2〔单位长度 / 秒〕.当 P 在线段 OB 上运动〔或O ≤t ≤3 〕时,OQ=t, OP=2t, S=t2 .当 P在线段 BA 上运动〔或 3 < t ≤8 〕时,OQ=t, AP=6+10-2t=16-2t,文档大全适用标准文案如图,做PD ⊥OA 于点D,由PDBO=APAB,得PD= 48-6t5.∴S= 12OQ ?PD=- 35t2+245t.〔 3〕当S= 485时,∵485 > 12 ×3×6∴点 P 在 AB 上当 S= 485 时, - 35t2+245t= 485∴t=4∴PD= 48-6×45= 245,AD=16-2×4=8AD= 82-(245)2= 325∴OD=8- 325= 85∴P〔85 ,245 〕M1 〔285 ,245 〕,M2 〔-125,245 〕,M3 〔125 ,-245〕评论:本题主要考察梯形的性质及勾股定理.在解题〔 2 〕时,应注意分状况进行议论,防备在解题过程中出现漏解现象.5. :如图,在直角梯形COAB 中, OC ∥ AB ,以 O 为原点成立平面直角坐标系,A, B,C 三点的坐标分别为 A(8,0), B (810),, C (0,4) ,点D为线段BC 的中点,动点P 从点 O 出发,以每秒 1 个单位的速度,沿折线OABD的路线挪动,挪动的时间为t 秒.〔 1〕求直线BC 的分析式;〔 2P 在线段 OA 上挪动,当 t 为什么值时,四边形OPDC 的面积是梯形2〕假定动点COAB 面积的?7〔 3〕动点P从点 O 出发,沿折线OABD 的路线挪动过程中,设△OPD 的面积为S ,请直接写出S 与 t 的函数关系式,并指出自变量t 的取值范围;ByD文档大全CO P A x适用标准文案6. 如图,△ ABC中,AB AC 10 厘米,BC 8 厘米,点 D 为 AB 的中点.〔 1 〕假如点P 在线段BC 上以3厘米/秒的速度由 B 点向 C 点运动,同时,点 Q 在线段CA 上由 C 点向 A 点运动.①假定点Q 的运动速度与点P 的运动速度相等,经过 1 秒后,△ BPD与△CQP能否全等,请说明原因;②假定点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,可以使△ BPD与△CQP全等?〔 2 〕假定点Q 以②中的运动速度从点 C 出发,点P 以本来的运动速度从点 B 同时出发,都逆时针沿△ ABC三边运动,求经过多长时间点P 与点 Q 第一次在△ ABC的哪条边上相遇?ADQB CP文档大全适用标准文案四边形中的动点问题课后作业1.如图,AD 与 BC 订交于E,∠1 =∠ 2 =∠3, BD = CD ,∠ADB = 90 °,CH ⊥ AB 于 H , CH 交 AD 于 F.(1 〕求证: CD ∥AB ;(2 〕求证:△ BDE ≌△ACE ;1〔 3 〕假定O 为 AB 中点,求证: OF =BE.22 、如图1―4 ―2l ,在边长为足 A E + CF=a ,说明:不论a 的菱形 ABCD 中,∠ E、F 如何挪动,三角形DAB = 60 °,E 是异于BEF 老是正三角形.A 、 D两点的动点, F 是CD上的动点,满3 、在平行四边形ABCD 中, E 为 BC 的中点,连结AE 并延伸交DC 的延伸线于点F.(1) 求证:AB CF ;(2) 当BC与AF知足什么数目关系时,四边形ABFC是矩形,并说明原因.DA文档大全CB EF适用标准文案4 、如图l- 4 - 80 ,正方形ABCD的对角线AC 、 BD 订交于点O , E 是 AC 上一点,过点 A 作 AG ⊥ EB,垂足为 G, AG 交 BD 于 F,那么 OE=OF .〔 1 〕请证明 0E=OF〔 2 〕解答〔1〕题后,某同学产生了以下猜想:对上述命题,假定点 E 在 AC 的延伸线上,AG ⊥ EB , AG 交EB 的延长线于G, AG 的延伸线交DB 的延伸线于点 F ,其余条件不变,那么仍有OE=OF.问:猜想所得结论能否成立?假定成立,请给出证明;假定不可立,请说明原因.5 、如图,在梯形ABCD中,AD ∥ BC, AD3, DC5, AB 4 2,∠B45 .M 从 B 点出发沿线段动点BC 以每秒 2 个单位长度的速度向终点 C 运动;动点N 同时从 C 点出发沿线段CD 以每秒 1 个单位长度的速度向终点 D 运动.设运动的时间为t 秒.(1 〕求BC的长.(2 〕当MN∥AB时,求t的值.A D〔 3 〕尝试究:t 为什么值时,△ MNC为等腰三角形.文档大全NB C适用标准文案6. 以下列图,有四个动点P、 Q 、 E、 F 分别从正方形ABCD 的四个极点出发,沿着AB、 BC、CD 、DA以相同的A FD速度向 B、C、 D、A 各点挪动。
人教版初中数学八下 小专题(十一) 四边形中的动点问题
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=12 cm,BC=18 cm,点P从点A出发,以1 cm/s的速度向点D运动;点Q从点C同时出发,以2 cm/s的 速度向点B运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点 P,Q运动的时间为t s.
在整个运动过程中,是否存在t值,使得四边形PQCD是菱形?若存在,请 求出t值;若不存在,请说明理由, 解:不存在.理由如下: 要使四边形PQCD是菱形,则四边形PQCD一定是平行四边形. 由母题知当t=4时,四边形PQCD是平行四边形, 此时DP=12-t=8(cm)≠10 cm,即DP≠DC, ∴按已知速度运动,四边形PQCD只能是平行四边形,但不可能是菱形.
(1)CD边的长为 10 cm,t的取值范围为 0≤t≤9 ;
(2)从运动开始,当t取何值时,PQ∥CD?
解:(2)设经过t s时,PQ∥CD,此时四边形PQCD为平行四边 形,则PD=CQ. 由题意,得PD=(12-t)cm,CQ=2t cm, ∴12-t=2t,解得t=4, ∴当t=4时,PQ∥CD.
(3)从运动开始,当t取何值时,PQ=CD?
解:(3)设经过t s时,PQ=CD.分别过点P,D作边BC的垂线 PE,DF,垂足分别为E,F. 当CF=EQ时,四边形PQCD为梯形(腰相等)或者平行四边形. ∵∠B=∠A=∠DFB=90°, ∴四边形ABFD是矩形,∴BF=AD=12 cm, ∴CF=BC-BF=6 cm. ①当四边形PQCD为梯形(腰相等)时, PD+2(BC-AD)=CQ, ∴(12-t)+12=2t,∴t=8, ∴当t=8时,PQ=CD; ②当四边形PQCD为平行四边形,由(2)知当t=4时,PQ=CD. 综上所述,当t=4或t=8时,PQ=CD.
初二数学《平行四边形中的动点问题》(附练习及答案)
四边形中的动点问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或直线上运动的一类开放性题目。
解决这类问题关键是动中求静,灵活运用有关数学知识。
数学思想:分类思想、函数思想、方程思想、数形结合思想、转化思想,其注重对几何图形运动变化能力的考查。
这类类问题从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理。
选择基本的几何图形,让学生经历探索的过程,以能力立意,考查自主探究能力,促进培养学生解决问题的能力。
解决这类问题首先要在动点的运动过程中观察图形的变化情况,需要画出图形在不同位置的情况,才能做好计算推理的过程;其次在变化中找到不变量的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
动点问题题型方法归纳:动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就四边形中的动点问题的常见题型作简单介绍,解题方法、关键给以点拨。
1、如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB =60°,则矩形ABCD的面积是_____________2、如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形EFGH 的面积为________(第1题)(第2题)(第3题)3、如图,正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为____________4、如图,在Rt△ABC中,∠B=90°,AC=60 cm,∠A=60°,点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t s(0 < t ≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由5、如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s 的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s);(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;(2)求当t为何值时,四边形ACFE是菱形;(3)是否存在某一时刻t,使以A、F、C、E为顶点的四边形内角出现直角?若存在,求出t的值;若不存在,请说明理由.6、在菱形ABCD中,∠B=60°,点E在射线BC上运动,∠EAF=60°,点F在射线CD上(1)当点E在线段BC上时(如图1),(1)求证:EC+CF=AB;(2)当点E在BC的延长线上时(如图2),线段EC、CF、AB有怎样的相等关系?写出你的猜想,不需证明7、如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.(1)求证:四边形AMDN是平行四边形;(2)填空:①当AM的值为______时,四边形AMDN是矩形;②当AM的值为______时,四边形AMDN是菱形.8、如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)探究:线段OE与OF的数量关系并加以证明;(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?(3)当点O在边AC上运动时,四边形BCFE会是菱形吗?若是,请证明,若不是,则说明理由.9、如图,已知菱形ABCD中,∠ABC=60°,AB=8,过线段BD上的一个动点P(不与B、D重合)分别向直线AB、AD作垂线,垂足分别为E、F.(1)BD的长是______;(2)连接PC,当PE+PF+PC取得最小值时,此时PB的长是______(第9题)(第10题)10、如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为______.11、如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD 的中点.(1)求证:四边形PMEN是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN是菱形;(3)四边形PMEN有可能是矩形吗?若有可能,求AP的长;若不可能,请说明理由.12、如图,在平行四边形ABCD中,对角线BD=12cm,AC=16cm,AC,BD相交于点O,若E,F 是AC上两动点,分别从A,C两点以相同的速度向C、A运动,其速度为0.5cm/s。
初中数学课件四边形的动点问题
应用练习
在四边形中, // , ⊥ , = 6, = 10,点从
出发以1/的速度向运动,点从点出发,以2/的速度向点运动,
当其中一点到达终点,而另一点也随之停止,设运动时间为,
(1)取何值时,四边形为矩形?
(2)是上一点,且 = 4,取何值时,以、、、为顶点的四边
线 AG 以 1cm/s 的速度运动, 点 F 从点 B 出发沿射线 BC 以 2cm/s 的速度运
动.如果点 E、F 同时出发,当四边形 AEFC 是平行四边形时, 运动时间 t 的
值为 ( )
A.2s
B.6s
C.8s
D.2s 或 6s
应用练习
如图,在梯形中, // ,点从点出发沿向点运动,同时点
形是平行四边形?
课堂小结
1. 根据速度与时间的关系表达线段长度
2. 根据矩形四个角都是90度,对边相等不变特征,找等量关系
3. 建立方程求解
4. 验证结论
若四边形为矩形且∠ = ∠ = 90o ,
//,则
= ,
即 = 26 − 3,
解得: = 6.5,
即 = 6.5时,四边形为矩形;
例题讲解
(2)∵ //,
∴ 若四边形为平行四边形,
则 = ,
即24 − = 3,
解得, = 6,
∴ 若四边形是平行四边形,则 = ,
∵ 已知点 的运动速度为1/ ,点 的运动速度为2/ , = 8 ,
= 4,
∴ 8 − 2 = ,
8
∴ = 3.
应用练习
如图,在等边三角形 ABC 中,AB=6cm,射线 AG∥BC,点 E 从点 A 出发沿射
边向点以3/的速度运动., 两点从, 两点同时出发,其中一点到达
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8四边形中的动点问题满分晋级阶梯四边形 8 级四边形7级四边形中的动点问题四边形 6 级特殊图形的旋转与正方形弦图平移和几何最值问题春季班春季班春季班第六讲第七讲第八讲漫画释义如法炮制知识互联网题型切片题型切片(两个)对应题目题由动点产生的特殊图例 1,例 2,例 3,练习 1,练习 2,练习3;型目例 4,例 5,例 6,例 7,练习4,练习 5.标由动点产生的函数关系编写思路本讲内容主要分为两个题型,题型一为由动点产生的特殊图形,例题主要是从单动点问题过渡到双动点问题,解决问题的主要策略为以静制动,分类讨论,寻找临界点.对于程度比较好的班级,给出了一个拓展版块,补充了线动及形动问题;题型二为由动点产生的函数关系,该版块重点是线段的含参表示,以及自变量的取值范围,请老师在课上进行重点强调.题型一:由动点产生的特殊图形思路导航我们常见的四边形中的动点问题可以总结为单动点问题与双动点问题.解决问题的主要策略为以静制动,分类讨论,寻找临界点.典题精练【例 1】已知如图:在平面直角坐标系中, O 为坐标原点,四边形 OABC 是矩形,点 A 、C的坐标分别为A(10,0)、C(0,4),点 D 是OA的中点,点 P 在BC边上运动,当△ODP是腰长为5的等腰三yCP B角形时,点P 的坐标为.(101 中学初三月考)【解析】 3 ,4 、2,4 或 8 ,4O DAx【例 2】在平行四边形ABCD 中,对角线 AC、 BD 相交于点 O,若 E、F 是 AC 上两动点,分别从A、C 两点以相同的速度1cm/s 向 C、 A 运动.⑴四边形 DEBF 是平行四边形吗 ?请说明理由.⑵若 BD =12cm, AC=16cm ,当运动时间t 为何值时,四边形DEBF 是矩形 ?D C D CFEO OEFA B BADCD CFEOOE FAB A B 【解析】⑴四边形 DEBF 是平行四边形理由:∵ E, F 两动点,分别从A,C 两点以相同的速度向C,A 运动∴AE=CF∴OE=OF∴BD、EF 互相平分∴四边形 DEBF 是平行四边形⑵ ∵四边形 DEBF 是平行四边形∴当 BD =EF 时,平行四边形DEBF 是矩形∵BD= 12cm,∴ EF= 12cm∴OE= OF =6cm∵AC= 16cm∴OA= OC=8cm∴AE= 2cm 或 AE= 14cm∵动点的速度是 1cm/s∴t= 2s 或 t= 14s【例 3】如图所示,在直角坐标系中,四边形 OABC 为直角梯形, OA∥ BC,BC=14cm ,A 点坐标为( 16,0), C 点坐标为( 0, 2).点 P、 Q 分别从 C、 A 同时出发,点 P 以 2cm/s 的速度由 C 向 B 运动,点 Q 以 4cm/s 的速度由 A 向 O 运动,当点 Q 停止运动时,点 P 也停止运动,设运动时间为ts 0 ≤ t ≤ 4 .⑴求当 t 为多少时,四边形 PQAB 为平行四边形?⑵求当 t 为多少时, PQ 所在直线将梯形OABC 分成左右两部分,其中左部分的面积为右部分面积的一半,求出此时直线PQ 的函数关系式.【解析】⑴ ∵ t s 后, BP= 14 2t cm,AQ =4t cm.由y7BP= AQ ,得 142t(s).4t , t=73P B∴当 t= s 时, BP= AQ ,又 OA∥ BC,C 3∴四边形 PQAB 为平行四边形.O Qx A⑵∵ C 点坐标为(0, 2), A 点坐标为( 16, 0),∴ OC=2 cm , OA=16 cm .∴S梯形 OABC =1(OA+BC ) ·OC=1×(16+14)×2=30(cm 2) .22∵ t s后,PC= 2t cm,OQ= 164t cm,∴S四边形 PQOC =116 4t2162t .2t2由题意可得 S四边形PQOC=10,∴162t10,解得 t=3s.此时直线 PQ 的函数关系式为 y x 4 .【探究】四边形中的动态问题【变式 1】如图,在矩形OABC 中,已知点 B 的坐标为 (9, 4),点 P 是矩形边上的一个动点,若点 E 的坐标为 (5, 0),且△POE 是等腰三角形,求点P 的坐标?yA P2P1By P3P4A BO E C xO E C x【解析】如图, 3 4,P22,4,P3 2.5,4,P49,3 .P1 ,【探究 2】多动点问题,注意多动点之间的联动情况,然后转化为单动点问题;【变式 2】如图,矩形ABCD 中, B 的坐标为 ( 4 3,4) ,一动点 P 从 O 出发,以每秒 1 个单位的速度,从点O 出发沿 OA 向终点 A 运动,同时动点Q 以每秒 2 个单位的速度从点O出发沿OB向终点B运动 . 过点Q作QE⊥ OB,交AB于点E,连接PE PQ. 设运动时间为t、秒 . 求t为何值时,PE OB.∥yA E BP QO C x16【解析】 PQ=BE 时, PE∥ OB,此时t.7【探究 3】线动问题,线动问题转化为点动问题;【变式 3】如图,矩形 ABCO 中, B 的坐标为 ( 4 3 ,4) ,一动点 P 从 O 出发,以每秒1 个单位的速度,从点 O 出发沿 OA 向终点 A 运动,过点 P 作直线 PF ⊥ OB ,交 OB 于点 F ;同时将直线 PF 以每秒3 个单位向右平移,分别交 AB 、 OB 于点 E 、Q ,连接 PE. 设运动时间为 t 秒 . 求 t 为何值时, PE ∥ OB.yAEBPFQOC x【解析】同上,此时 t16 .7【探究 4】形动问题,形动问题通过转化为线动问题,从而转化为点动问题;【变式 4】如图,直角 Rt △ ABO 中, A 的坐标为 (15, 53 ),斜边中线 AC 将这个直角三角形分成了2 2两个等腰三角形△ AOC 与△ ABC (如图所示) ,将△ AOC 沿直线 x 轴正方向平移得到△ A 1O 1C 1 ,当点 O 1 与点 C 重合时,停止平移。
在平移的过程中, A 1O 1 与 OB 交于点 D ,O 1 B 1与 BC 交于点 E.设平移距离 OO 1 为 x , △ A 1O 1 C 1 与△ ABC 重叠部分的面积为 y ,是否存在这样的 x,使得重叠部分面积等于原△ABO 面积的1?若存在,请求出x 的值;若不存在,4请说明理由.yAyAA1PEFO CB x O O 1C C 1Bx5【解析】 x.2题型二:由动点产生的函数关系典题精练【例 4】⑴如图 1,在矩形 MNPQ 中,动点 R 从点 N 出发,沿 N→ P→ Q→ M 方向运动至点M 处停止.设点 R 运动的路程为x ,△MNR的面积为y,如果y关于的函数图象如图 2 所示,则当x9 时,点 R 应运动到()( 161 期中)A .N 处B. P 处C.Q 处 D .M 处Q P yRM NO49x图 1图 2⑵如图,在矩形ABCD 中, AB=2,BC=1,动点 P 从点 B 出发,沿路线B→ C→ D 作匀速运动,那么△ ABP 的面积 S 与点 P 运动的路程x之间的函数图象大致是()(重庆中考)D CPA BS S S S332111O 13 x O13x O 3 x O1 3 xA .B .C. D .【解析】⑴ C;⑵ B.【例 5】正方形 ABCD 的边长为 2 厘米,点 E 从点 A 开始沿 AB 边移动到点B,点F 从点 B 开始沿 BC 边移动到点 C,点 G 从点 C 开始沿 CD 边移动到GD C H⑴求证:△ HAE ≌△ EBF ;⑵设四边形 EFGH 的面积为 S(平方厘米),求 S 与 t 之间的函数关系式,并写出自变量t 的取值范围;【解析】⑴ t 秒时, AE=0. 5t, BF=0. 5t, DH =0.5t∴ AE=BF=DH∵四边形 ABCD 为正方形∴∠ A=∠ B=90°, AD=AB∴ AH=BE= 20.5t∴△ HAE≌△ EBF⑵由⑴同理可得 Rt△ HAE , Rt△ EBF , Rt△FCG 以及 Rt △ GDH 四个三角形两两全等S 41(20.5t)41240.5t t2t22自变量 t 的取值范围是 0 ≤ t ≤ 4【例 6】如图,已知正方形ABCD 与正方形 EFGH 的边长分别是42 和 2 2 ,它们的中心 O1,O2都在直线 l 上, AD ∥ l , EG 在直线 l 上, l 与 DC 相交于点M ,ME72 2 ,当正方形 EFGH沿直线l 以每秒 1 个单位的速度向左平移时,正方形ABCD 也绕 O1以每秒 45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.( 1)在开始运动前,1 2;O O( 2)当两个正方形按照各自的运动方式同时运动3秒时,正方形ABCD 停止旋转,这时AE, O1O2;( 3)当正方形ABCD 停止旋转后,正方形EFGH 继续向左平移的时间为x 秒,两正方形重叠部分的面积为y ,求 y 与x之间的函数表达式.A D HO1O2lM E GB C F【解析】( 1) 9.( 2) 0, 6.B B BH H HO1C O1O2l C O1O2l O2A lE A G E G A E C GF F FD D D图 1图 2图 3( 3)当正方形 ABCD 停止运动后,正方形EFGH 继续向左平移时,与正方形ABCD 重叠部分的形状也是正方形.重叠部分的面积y 与x之间的函数关系应分四种情况:①如图 1,当 0 ≤ x 4 时,∵ EA x ,∴ y 与 x 之间的函数关系式为y x2.22③如图 3,当 8 ≤ x12 时,∵ CG 12x ,122x1 x212x 72 .∴ y 与 x 之间的函数关系式为 y22④当 x≥ 12 时,y与x之间的函数关系式为y0 .真题赏析【例 7】将一矩形纸片 OABC 放在平面直角坐标系中, O 为原点,点 A 在x轴上,点 C 在 y 轴上,OA=10 ,OC=8.⑴如图 1 在 OC 边上取一点 D ,将△ BCD 沿 BD 折叠,使点 C 恰好落在 OA 边上,记作 E 点;①求点 E 的坐标及折痕DB 的长;②在 x 轴上取两点 M、 N(点 M 在点 N 的左侧),且 MN 4.5 ,求使四边形 BDMN 的周长最短的点 M、点 N 的坐标.⑵如图 2,在 OC、CB 边上选取适当的点 F 、G,将△ FCG 沿 FG 折叠,使点 C 落在 OA 上,记为 H 点,设 OH = x,四边形 OHGC 的面积为 S.求: S 与x之间的函数关系式,并指出变量 x 的取值范围.y yGC B C BDFO E A x xO HA图 1【解析】⑴ ①在矩形 OABC 中, BC=OA=10 , BA=OC=8.由折叠可知:△CBD ≌ △EBD ,∴ BE=BC=10 .在 Rt△BAE 中, EA= BE2BA2=6.OE=OA-AE=4 ,∴ E(4,0) .设 CD=x,∵△ CBD ≌ △ EBD ,∴DE =CD =x, OD =8-x.,在Rt△ODE 中, DE 2 =OD 2+ OE2,∴ x2 =( 8-x)2+ 42,∴ x =5.在 Rt△CDB 中, BD =CD 2BC 2= 5 5②要使 DB+ DM+MN+BN 最短,只需要 DM+BN 最短.将点 B(10 , 8 )向左平移 4. 5 个单位长度,得图2yB1C B∴BB 1= 4.5∵ MN=4 . 5, ∴ BB 1∥ M N ,∴ BNMB 1 是平行四边形. ∴ B 1M = BN .作 D 关于 x 轴的对称点 D 1(0, -3) , 连接 B 1D 1,由对称性及两点之间线段最短可知: B 1D 1 与 x 轴的交点为所求 M 点,在 x 轴上点 M 的右侧作 MN =4. 5,得所求 N 点.可求得直线 B 1D 1 的解析式为 y 2x 3 ,∴ M ( 3, 0 ), N(6,0 ). 2⑵过点 G 作 GK ⊥ OA 于 K ,设 CG = y ,∴ OK=CG = y , GK =OC = 8. 由折叠可知: △ CGF ≌△ HGF , ∴ GH=CG = y ,∴ HK = OK -OH==y -x .在 Rt △ HKG 中, HG 2 =HK 2+ GK 2,∴ y 22y x82 ,yGCBFxOHK Ay64 x 2 , 2xS1(OH CG ) OC1( x 64 x 2) 8 6x21284 ≤ x ≤ 8 .22 2xx思维拓展训练 ( 选讲 )训练 1.如图,在直角梯形ABCD 中, DC ∥ AB , A90 , AB28cm ,DC 24cm , AD4cm ,点M从点D出发,以 1cm/ s 的速度向点 C运动,点 N 从点B同时出发,以 2cm/ s 的速度向点A运动,当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形ANMD 的面积 y(cm2) 与两动点运动的时间t( s) 的函数图象大致是()D M CA N By yy y565656562828O14t O28t O28 tO14tA .B .C.D.【解析】解析式为 y562t 0t 14∴选 D训练 2.如图,在梯形ABCD 中, AD //BC,E 是 BC 的中点, AD=5,BC =12, CD= 4 2,∠ C=45°,点P 是 BC 边上一动点,设PB 的长为 x.A D⑴当 x 的值为 ____________时,以点 P、A、D、E为顶点的四边形为平行四边形;⑵点 P 在 BC 边上运动的过程中,以点P、A、D、E为顶点的四边形能否构成菱形?试说明理由.(河南中考)B P E C 【解析】⑴ 1或 11.⑵由⑴知,当BP时,以点 P、A、D、E 为顶点的四边形为平行四边形.11∴ EP AD5过 D 作DF BC 于F,则 DF FC 4 ,∴ FP 3 .∴ DP FP 2DF 232425∴EP DP ,故此时平行四边形是菱形.以点 P、A、D、E 为顶点的四边形构成菱形.训练 3.已知:等边三角形ABC 的边长为 4 厘米,长为 1 厘米的线段MN 在△ABC 的边AB上沿AB方向以1厘米 /秒的速度向B点运动(运动开始时,CP QA M D N B别作 AB 边的垂线,与 △ ABC 的其它边交于 P 、 Q 两点,线段 MN 运动的时间为 t 秒. ⑴ 线段 MN 在运动的过程中, t 为何值时,四边形 MNQP 恰为矩形?并求出该矩形的面积; ⑵ 线段 MN 在运动的过程中,四边形 MNQP 的面积为 S ,运动的时间为 t .求四边形 MNQP 的面积 S 随运动时间 t 变化的函数关系式,并写出自变量 t 的取值范围.【解析】 ⑴ 过点 C 作 CDAB ,垂足为 D .则 AD 2 ,当 MN 运动到被 CD 垂直平分时,四边形 MNQP 是矩形,即 AM3时,四边形 MNQP 是矩形,2∴ t3秒时,四边形 MNQP 是矩形.23∵ PM,323∴S 四边形 MNQP3 .2CQPA MNB⑵ ①当 0 t1时,S 四边形 MNQP1PM QN MN1 3tC3 t 1 122Q3t 3 ; P② 当 12 2 时t≤≤S1 PM QN MN 1 3t3 3 t 1 四边形 MNQP223 3 ; 2AMNB③ 当 2 t 3 时,CPS 四边形 MNQP1PM QN MN1 3 4 t3 3 t 1227 3 . Q3t2【点评】 像本题第一问这样是否存在特殊图形的问题,应先把特殊图形画MN B出,再根据图形引出的特殊条件进行求解.A训练 4. 如图所示, 在直角坐标系中,矩形 ABCD 的边 AD 在 x 轴上, 点 A 在原点, AB =3 ,AD =5 .若矩形以每秒 2 个单位长度沿 x 轴正方向作匀速运动.同时点 P 从 A 点出发以每秒1 个单位长度沿 A -B -C -D 的路线作匀速运动.当 P 点运动到 D 点时停止运动,矩形ABCD 也随之停止运动.⑴ 求 P 点从 A 点运动到 D 点所需的时间;⑵ 设 P 点运动时间为t (秒)①当 t= 5 时,求出点 P 的坐标;yBC②若△ OAP 的面积为 S ,试求出s 与 t 之间的函数关系式(并写出相应的自变量t 的取值范围).【解析】⑴ P 点从 A 点运动到 D 点所需的时间=(3+5+3)÷1= 11(秒)⑵ ①当 t= 5 时, P 点从 A 点运动到BC 上,此时 OA=10 , AB+BP=5,∴ BP=2过点 P 作 PE⊥ AD 于点 E,则 PE=AB=3, AE=BP=2∴OD=OA+AE =10+2=12∴点 P 的坐标为( 12,3).②分三种情况:i.当 0 t ≤ 3 时,点 P 在 AB 上运动,此时OA=2 t,AP=t∴S = 1×2t×t= t 22ii .当 3 t ≤ 8 时,点 P 在 AB 上运动,此时OA=2t1∴ S =×2t×3=3 t2iii .当 8< t<11 时,点 P 在 CD 上运动,此时OA=2t, AB+BC+CP= t ∴DP= ( AB+BC+CD) (AB +BC +CP )= 11 t∴ S = 1×2t×(11 t)=t2+11t 2综上所述,S 与 t 之间的函数关系式是:当 0 t ≤ 3 时, S = t2;当 3 t ≤ 8 时, S =3 t;当 8< t< 11 时, S =t 2 +11 t复习巩固题型一由动点产生的特殊图形巩固练习【练习 1】如图,在矩形 OABC 中,已知A 、C 两点的坐标分别为 A 4,0 、 C 0,2,为 OA 的中点.设D点 P 是AOC平分线上的一个动点(不与点O 重合).⑴ 试证明:无论点P 运动到何处,PC总与 PD 相等;⑵当点 P 运动到与点 B 的距离最小时,求P 的坐标;⑶ 已知 E (1,- 1),当点 P 运动到何处时, △ PDE 的周长最小?求出此时点 P 的坐标和△ PDE 的周长; (四中期中 )【解析】⑴ 可证 △ OPC ≌△ OPD .⑵ P 3,3y⑶ 由 C 0,2 、 E 1, 1 可知,直线 CE 的解析式 CB为 y3 x 2与直线 y x 相交于点 P (1,1).P22则C △ PDE CEED 12321212102 .ODAx【练习 2】 平面直角坐标系中,四边形OABC 为矩形,点 A 、 B 的坐标分别为(M .N 分别从 O 、B 同时出发,以每秒 1 个单位的速度运动.其中,点 动,点 N 沿 BC 向终点 C 运动.过点 N 作 NP ⊥ BC ,交 AC y 于 P ,连接 MP .已知动点运动了 x 秒.请你探索:若 P 点 坐标为 ( 3-x , 4x )当 x 为何值时, △ MPA 是一个等腰三角3C形?有几种情况?写出研究成果并证明. 【解析】当 x=1,或 x54,或 x9时, △ MPA 是一个等腰三角形4383, 0),( 3, 4).动点 M 沿 OA 向终点 A 运N BP延长 NP 交 x 轴于 Q ,则有 PQ ⊥ OA① 若 MP=PA ∵ PQ ⊥ MA OM A∴ MQ=QA=x∴ 3 2xx , ∴ x=1y② 若 MP=MA ,则 MQ = 3 2x , PQ= 4x , PM =MA= 3 xN3 CB在 Rt △PMQ 中, ∴ PM 2 MQ 2 PQ 2 ,∴ (3 x)2(3 2x)2( 4 x) 2 ∴ x 54 P343③ 若 PA=AM , ∴ PA= 5x , AM= 3 xOMQA3 ∴ 5x 3x ∴ x9 38综上所述, x=1,或 x54,或 x9438【练习 3】 如图,在直角梯形 COAB 中, OC//AB ,以 O 为原点建立平面直角坐y标系, A 、 B 、 C 三点的坐标分别为 A(8,0), B(810),, C (0,4) ,点 D 为 D线段 BC 的中点,动点P 从点 O 出发,以每秒 1 个单位的速度,沿折线OABD 的路线移动,移动的时间为 t 秒.C⑴求直线 BC 的解析式;⑵若动点 P 在线段 OA 上移动,当 t 为何值时,四边形 OPDC 的面积是梯形 COAB 面积的 2.OP7xxBAx【解析】⑴ 直线 BC 的解析式为3y= x+44⑵ 过点 D 作 DM ⊥y 轴,垂足为 M在 Rt △ CDM 中, CD1CB 5 ,DM4 ,CM2∴S 四边形 OPDCS △ OCD S △ OPD1 4 412 7t2梯形 COAB 的面积 S 梯形 COAB110) 8 56(42解方程 7t8256 解得 t16277因此,当 t16时,四边形 OPDC 的面积是梯形 7yBDM 3C7t 82OPAx2COAB 的面积的.题型二由动点产生的函数关系 巩固练习【练习 4】 如图,三个大小相同的正方形拼成六边形ABCDEF ,一动点 P 从点 A 出发沿着A →B →C →D →E 方向匀速运动, 最后到达点 E .运动过程中△ PEF 的面积( s )随时间( t )变化的图象大致是()ssssPA ·.OtOOt OFtt .BCAD【解析】B.。
