2013届高考数学一轮复习课件(理)浙江专版-第20讲 简单的三角恒等变换
合集下载
高三数学一轮复习 第三章 第六节 简单的三角恒等变换课件
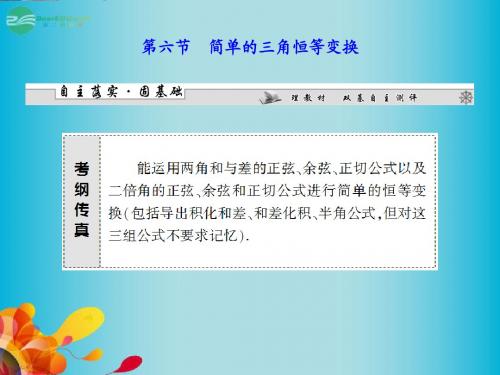
π π π (2)∵cos 2α=sin( +2α)=2sin(α+ )cos(α+ ), 2 4 4 cos 2α π π ∴ =2cos(α+ )=2sin( -α), 4 4 π sin( +α) 4 π π 12 又0<α< 且cos( -α)= , 4 4 13 π ∴sin( -α)= 4 5 = , 13 π 1-cos ( -α)= 4
α cos sin 2 【尝试解答】 原式=( - α sin cos 2 2α 2α cos -sin 2 2 sin α = · α α cos α sin ·cos 2 2 2cos α sin α = · =2. sin α cos α
α 2sin2α 2 )· α 2sin αcos α 2
π π π 当2x+ =- ,即x=- 时,f(x)有最小值-1. 4 4 4 π π ∴f(x)在区间[- , ]上的最大值、最小值分别是 2 4 4 和-1.
易错提示:(1)化简解析式时出错,导致错误答案. π (2)求最值时,误把x的范围当成2x+ 的范围,导致错 4 误答案. 防范措施:(1)化简解析式,把函数式转化为Asin(ωx+ φ)的形式是解答本题的关键,因此求解时应力求准确,必 要时应进行检验,看化简结果是否正确. (2)求函数y=Asin(ωx+φ)的最值或值域时,可令t=ωx +φ,然后根据x的范围确定t的范围,最后可根据y=sin t的 图象,确定函数的最值或值域.
x x 已知sin -2cos =0. 2 2 (1)求tan x的值; cos 2x (2)求 的值. π 2cos( +x)· x sin 4 x x x 【解】 (1)由sin -2cos =0,得tan =2, 2 2 2
2×2 4 ∴tan x= = =- . x 1-22 3 2 1-tan 2 x 2tan 2
高考数学一轮复习 第20讲 简单的三角恒等变换课件 理 (浙江专)

素材3
求证:sins2iαnα+β-2cos(α+β)=ssiinnβα.
11、凡为教者必期于达到不须教。对人以诚信,人不欺我;对事以诚信,事无不成。 12、首先是教师品格的陶冶,行为的教育,然后才是专门知识和技能的训练。 13、在教师手里操着幼年人的命运,便操着民族和人类的命运。2022/1/182022/1/18January 18, 2022 14、孩子在快乐的时候,他学习任何东西都比较容易。 15、纪律是集体的面貌,集体的声音,集体的动作,集体的表情,集体的信念。 16、一个人所受的教育超过了自己的智力,这样的人才有学问。 17、好奇是儿童的原始本性,感知会使儿童心灵升华,为其为了探究事物藏下本源。2022年1月2022/1/182022/1/182022/1/181/18/2022 18、人自身有一种力量,用许多方式按照本人意愿控制和影响这种力量,一旦他这样做,就会影响到对他的教育和对他发生作用的环境。 2022/1/182022/1/18
第20讲 简单的三角恒等变换
一 恒等变换下的化简求值
【例 1】已知 sin2x-2cos2x=0,求 2cosco4πs+2xx·sinx的值s2αcos2β-12cos2αcos2β 的值为
1 2
.
二 恒等变换下的拆角求值
【例 2】(1)已知 tan(α+β)=25,tan(β-π4)=14,求 tan(π4+α) 的值;
(2)scions77°°+-csoisn1155°°·ssiinn88°°=__________.
素材2
若 cos(π4+x)=35,1172π<x<74π,求sin21x-+ta2nsxin2x的值.
三 恒等变换下的三角证明
【例 3】证明:2-2sicnoαs4+α-34πsicno4αsα+π4=11+ -ttaannαα.
2013年高考数学成功方案系列课件第三章第四节简单的三角恒等变换

∴-π2<α-β<0.
∴sin(α-β)=- 1-cos2α-β=- 47,
∴tan(α-β)=csionsαα--ββ=- 37.
[答案]
-
7 3
1.定义运算 a
b=a2-ab-b2,则 sin
π 6
π6= ( )
A.-12-
3 4
B.-12+
3 4
C.-12
解析:sin
π 6
D.
(2)∵tan α=-13,∴5sin2α2+8sin2sα2incoαs-α2+π411cos2α2-8
=5sin2α2+cos2α2si+n α4-sincoαs+α6·1+c2os α-8
=5+4sinsinα+α-3+co3scαos
α-8=4sin sin
α+3cos α α-cos α
所以π6≤2x-π3≤23π,则有12≤sin(2x-π3)≤1. 因为函数f(x)=4sin2(π4+x)-2 3cos 2x+t(x∈P)的最小值为3, 所以4×12+2+t=3,解得t=-1. (2)因为2+m<f(x)在x∈P上恒成立,则由已知可得2+m<3,得 m<1,故m的取值范围是(-∞,1).
α·(1+csoins
α sin α·
α 2 α)
sin 2cos2
cos2
α
α
=2scionsαα+2scionsαα·csoins αα·scionsα22=2scionsαα+2csionsα22
=2scionsαα+4ssiinn2αα2=2cos
α+4sin2α2 sin α
=21-2sisni2nα2α+4sin2α2
.
解析:sin 2A=2sin Acos A=-34<0. 又 A 为△ABC 的内角,∴sin A>0,cos A<0.
(浙江专用)高考数学一轮复习讲练测专题4.3简单的三角恒等变换(讲)(含解析)

4.备考重点: (1) 掌握和差倍半的三角函数公式; (2) 掌握三角函数恒等变换的常用技巧.
知识点 1.两角和与差的三角函数公式的应用 两角和与差的正弦、余弦、正切公式
C(α-β):cos(α-β)=cosαcosβ+sinαsinβ;
C(α+β):cos(α+β)=cosαcos_β-sin_αsinβ;
,则
故 tan2 故选:A
考点 1 两角和与差的正弦函数、余弦函数公式的应用
【典例 3】(2019·北京高考模拟(文))如图,在平面直角坐标系 xOy 中,角 与角 均以 Ox 为始边,
终边分别是射线
OA
和射线
OB.射线
OA,OC
与单位圆的交点分别为
A
3 5
,
4 5
,
C(1, 0)
.若
BOC
【典例 4】(2018 年全国卷 II 文)已知
【答案】 . 【解析】
,则
__________.
,
解方程得
.
【规律方法】
1.运用两角和与差的三角函数公式时,不但要熟练,准确,而且要熟悉公式的逆用及变形,如 tan α+tan
β=tan(α+β)·(1-tan αtan β)和二倍角的余弦公式的多种变形等.
【典例 5】(2016·全国高考真题(理))若
A. 7 25
【答案】D
【解析】
B. 1 5
C. 1 5
,则 sin 2 ( ) D. 7 25
,
且
,故选 D.
【总结提升】 转化思想是实施三角变换的主导思想,恒等变形前需清楚已知式中角的差异、函数名称的差异、运算结构 的差异,寻求联系,实现转化.注意三角函数公式逆用和变形用的 2 个问题 (1)公式逆用时一定要注意公式成立的条件和角之间的关系.
知识点 1.两角和与差的三角函数公式的应用 两角和与差的正弦、余弦、正切公式
C(α-β):cos(α-β)=cosαcosβ+sinαsinβ;
C(α+β):cos(α+β)=cosαcos_β-sin_αsinβ;
,则
故 tan2 故选:A
考点 1 两角和与差的正弦函数、余弦函数公式的应用
【典例 3】(2019·北京高考模拟(文))如图,在平面直角坐标系 xOy 中,角 与角 均以 Ox 为始边,
终边分别是射线
OA
和射线
OB.射线
OA,OC
与单位圆的交点分别为
A
3 5
,
4 5
,
C(1, 0)
.若
BOC
【典例 4】(2018 年全国卷 II 文)已知
【答案】 . 【解析】
,则
__________.
,
解方程得
.
【规律方法】
1.运用两角和与差的三角函数公式时,不但要熟练,准确,而且要熟悉公式的逆用及变形,如 tan α+tan
β=tan(α+β)·(1-tan αtan β)和二倍角的余弦公式的多种变形等.
【典例 5】(2016·全国高考真题(理))若
A. 7 25
【答案】D
【解析】
B. 1 5
C. 1 5
,则 sin 2 ( ) D. 7 25
,
且
,故选 D.
【总结提升】 转化思想是实施三角变换的主导思想,恒等变形前需清楚已知式中角的差异、函数名称的差异、运算结构 的差异,寻求联系,实现转化.注意三角函数公式逆用和变形用的 2 个问题 (1)公式逆用时一定要注意公式成立的条件和角之间的关系.
简单的三角恒等变换优秀课件(4个课件)

思考6:参照上述分析,cosα cosβ , sinα sinβ 分别等于什么?其变换功能 如何?
1 c o sc a o s b = c o s ( ab ++ )c o s ( ab -) [ ] 2
1 s i n a s i n b = -[ c o s ( ab +)c o s ( ab -) ] 2
作业: P143习题3.2A组: 1(5)(6)(7)(8) ,2,3,4,5.
19、一个人的理想越崇高,生活越纯洁。 20、非淡泊无以明志,非宁静无以致远。 21、理想是反映美的心灵的眼睛。 22、人生最高之理想,在求达于真理。 便有了文明。 24、生当做人杰,死亦为鬼雄。 25、有理想的、充满社会利益的、具有明确目的生活是世界上最美好的和最有意义的生活。 26、人需要理想,但是需要人的符合自然的理想,而不是超自然的理想。 27、生活中没有理想的人,是可怜的。 28、在理想的最美好的世界中,一切都是为美好的目的而设的。 29、理想的人物不仅要在物质需要的满足上,还要在精神旨趣的满足上得到表现。 30、生活不能没有理想。应当有健康的理想,发自内心的理想,来自本国人民的理想。 31、理想是美好的,但没有意志,理想不过是瞬间即逝的彩虹。 32、骐骥一跃,不能十步;驽马十驾,功在不舍;锲而舍之,朽木不折;锲而不舍,金石可镂。——荀况 33、伟大的理想只有经过忘我的斗争和牺牲才能胜利实现。 34、为了将来的美好而牺牲了的人都是尊石质的雕像。 35、理想对我来说,具有一种非凡的魅力。 36、扼杀了理想的人才是最恶的凶手。 37、理想的书籍是智慧的钥匙。 人生的旅途,前途很远,也很暗。然而不要怕,不怕的人的面前才有路。—— 鲁 迅 2 人生像攀登一座山,而找寻出路,却是一种学习的过程,我们应当在这过程中,学习稳定、冷静,学习如何从慌乱中找到生机。 —— 席慕蓉 3 做人也要像蜡烛一样,在有限的一生中有一分热发一分光,给人以光明,给人以温暖。—— 萧楚女 4 所谓天才,只不过是把别人喝咖啡的功夫都用在工作上了。—— 鲁 迅 5 人类的希望像是一颗永恒的星,乌云掩不住它的光芒。特别是在今天,和平不是一个理想,一个梦,它是万人的愿望。—— 巴 金 6 我们是国家的主人,应该处处为国家着想。—— 雷 锋 7 我们爱我们的民族,这是我们自信心的源泉。—— 周恩来 8 春蚕到死丝方尽,人至期颐亦不休。一息尚存须努力,留作青年好范畴。—— 吴玉章 9 学习的敌人是自己的满足,要认真学习一点东西,必须从不自满开始。对自己,“学而不厌”,对人家,“诲人不倦”,我们应取这种态度。—— 毛泽东 10 错误和挫折教训了我们,使我们比较地聪明起来了,我们的情就办得好一些。任何政党,任何个人,错误总是难免的,我们要求犯得少一点。 犯了错误则要求改正,改正得越迅速,越彻底,越好。—— 毛泽东 38、理想犹如太阳,吸引地上所有的泥水。 9.君子欲讷于言而敏于行。 ——《论语》 译:君子不会夸夸其谈,做起事来却敏捷灵巧。 10.二人同心,其利断金;同心之言,其臭如兰。 ——《周易》 译:同心协力的人,他们的力量足以把坚硬的金属弄断;同心同德的人发表一致的意见,说服力强,人们就像嗅到芬芳的兰花香味,容易接受。 11.君子藏器于身,待时而动。 ——《周易》 译:君子就算有卓越的才能超群的技艺,也不会到处炫耀、卖弄。而是在必要的时刻把才能或技艺施展出来。 12.满招损,谦受益。 ——《尚书》 译:自满于已获得的成绩,将会招来损失和灾害;谦逊并时时感到了自己的不足,就能因此而得益。 13.人不知而不愠,不亦君子乎? ——《论语》 译:如果我有了某些成就,别人并不理解,可我决不会感到气愤、委屈。这不也是一种君子风度的表现吗?知缘斋主人 14.言必信 ,行必果。 ——《论语》 译:说了的话,一定要守信用;确定了要干的事,就一定要坚决果敢地干下去。 15.毋意,毋必,毋固,毋我。 ——《论语》 译:讲事实,不凭空猜测;遇事不专断,不任性,可行则行;行事要灵活,不死板;凡事不以“我”为中心,不自以为是,与周围的人群策群力,共同完成任务。 16.三人行,必有我师焉,择其善者而从之,其不善者而改之。——《论语》 译:三个人在一起,其中必有某人在某方面是值得我学习的,那他就可当我的老师。我选取他的优点来学习,对他的缺点和不足,我会引以为戒,有则改之。 17.君子求诸己,小人求诸人。 ——《论语》 译:君子总是责备自己,从自身找缺点,找问题。小人常常把目光射向别人,找别人的缺点和不足。很多人(包括我自己)觉得面试时没话说,于是找了一些名言,可以在答题的时候将其穿插其中,按照当场的需要或简要或详细解释一番,也算是一种应对的方法吧 1.天行健,君子以自强不息。 ——《周易》 译:作为君子,应该有坚强的意志,永不止息的奋斗精神,努力加强自我修养,完成并发展自己的学业或事业,能这样做才体现了天的意志,不辜负宇宙给予君子的职责和才能。 2.勿以恶小而为之,勿以善小而不为。 ——《三国志��
高考一轮数学文科:第20讲-简单的三角恒等变换ppt课件

α= α
1(_3+_)_降c_2o_s幂_α_公_,式t:ans2α2in=2 2_11_=- +___cc_oo__ss___2αα__.___,cos2 2 =
(4)tanα2 =_1_+s_i_cno_s_α_α_=_1-__sci_no_sα_α__.
2.常见的几种角的变换
(1)α=(α+β)-_____β___,α=__(_α_-__β_) _+β.
课堂考点探究
探究点二 三角函数式的求值
考向1 给值求值
例 2 (1)[2016·辽宁丹东二模] 若 sin 2α=23,则 tan
α+ 1
tan
α=(
)
A. 3 B. 2 C.3 D.2
(2)[2016·甘肃天水一中四模] 已知 cosα-π6 +sin α=453,则 sinα+76π的值是________.
都表示为 10°的三角函数,约 分即得结果.
课堂考点探究
[答案] (1)12
(2)
3 2
[解析] (1)1+sins2in501°0°=2(1-1+cossin11000°°)=1-2c(os1(+9s0i°n 1+0°10)°)=2(11++ssiinn1100°°)=12.
(2)原式=4sin21c0o°s21c0o°s 10°-sin 10°csoins 55°°-csoins 55°°=
(2)2α=(α+β)+__(_α_-__β)__,2β=__(α_+__β_)__-
(α-β).
(3)
α+β
α2
=
__α__-__β2_ _
-
α2 -β
,
α
=
2
×
____2____.
3.常数的变换
三角恒等变换复习公开课精华ppt课件

例3 :已知 A、B、C是△ABC三内角,向量
m (1 , 3) , n (cos A , sin A) , m n 1 .
(1)求角
A;(2)若
1 sin2B cos2 B sin2
B
3
,
求
tanC
.
解:(1) m n 1 ,
(1 , 3 ) (cos A , sin A) 1 ,
tan2 sin Asin B tan (sin Acos B cos Asin B) cos Acos B 2
5
典型例题
tan2 sin Asin B tan sin( A B) cos Acos B 2 ①
5
因为 C 3π ,A+B= π , 所以 sin(A+B)= 2 ,
θ
为第二象限角,若
tan
π 4
1 2
,则
sin θ+cos θ=__________.
分析:由 tan
π 4
1 1
tan tan
1 ,得 2
tan
θ= 1 , 3
即 sin θ= 1 cos θ. 3
将其代入 sin2θ+cos2θ=1,得 10 cos2 1 .
9
因为 θ 为第二象限角,所以 cos θ= 3 10 ,sin θ= 10 ,
4
4
2
因为 cos(A+B)=cos Acos B-sin Asin B,
即 3 2 -sin Asin B= 2 ,解得 sin Asin B= 3 2 2 2 .
5
2
5 2 10
由①得 tan2 5 tan 4 0
解得 tan 1或tan 4.
变式3:
(2013·辽宁理)设向量 a
2013届高考一轮复习(理数,浙江)-第20讲 简单的三角恒等变换

2
7 = . 25
17π 7π 5π π 因为 <x< ,则 <x+ <2π, 12 4 3 4 π 4 故 sin( +x)=- , 4 5 π sin +x π 4 4 tan( +x)= =- , 4 π 3 cos +x 4 7 4 28 故原式= ×(- )=- . 25 3 75
三
恒等变换下的三角证明
3π π 2-2sinα+ cosα+ 4 4 1+tanα 【例 3】证明: = . 4 4 cos α-sin α 1-tanα
π 2-2cos α+4 【证明】左边= cos2α-sin2α
2
π 2sin α+4 = 2 cos α-sin2α
2
π 1-cos2α+2 = cos2α-sin2α 1+sin2α = 2 cos α-sin2α
sin15° +cos15° -8° sin8° (2)原式= cos15° -sin15° -8° sin8° 1-cos30° sin15°cos8° · = =tan15° = cos8° cos15° sin30° =2- 3.
【点评】进行三角变换的技巧是变角,即注意角的和、差、 倍、半、互余、互补关系根据实际情况对角进行“拆”或 “添”变形,这样可大大减少运算量.基本的解题规律为: 观察差异(或角、或函数、或运算),寻找联系(借助熟知的公 式、方法或技巧),综合分析,实现转化.
三角恒等变形的实质是对角、函数名称及运算结 构的转化,而转化的依据就是一系列的三角公式, 因此对三角公式在实现这种转化中的应用应有足 够的了解:
1同角三角函数关系——可实现函数名称的转化. 2 诱导公式及和、差、倍角的三角函数——可以
实现角的形式的转化.
7 = . 25
17π 7π 5π π 因为 <x< ,则 <x+ <2π, 12 4 3 4 π 4 故 sin( +x)=- , 4 5 π sin +x π 4 4 tan( +x)= =- , 4 π 3 cos +x 4 7 4 28 故原式= ×(- )=- . 25 3 75
三
恒等变换下的三角证明
3π π 2-2sinα+ cosα+ 4 4 1+tanα 【例 3】证明: = . 4 4 cos α-sin α 1-tanα
π 2-2cos α+4 【证明】左边= cos2α-sin2α
2
π 2sin α+4 = 2 cos α-sin2α
2
π 1-cos2α+2 = cos2α-sin2α 1+sin2α = 2 cos α-sin2α
sin15° +cos15° -8° sin8° (2)原式= cos15° -sin15° -8° sin8° 1-cos30° sin15°cos8° · = =tan15° = cos8° cos15° sin30° =2- 3.
【点评】进行三角变换的技巧是变角,即注意角的和、差、 倍、半、互余、互补关系根据实际情况对角进行“拆”或 “添”变形,这样可大大减少运算量.基本的解题规律为: 观察差异(或角、或函数、或运算),寻找联系(借助熟知的公 式、方法或技巧),综合分析,实现转化.
三角恒等变形的实质是对角、函数名称及运算结 构的转化,而转化的依据就是一系列的三角公式, 因此对三角公式在实现这种转化中的应用应有足 够的了解:
1同角三角函数关系——可实现函数名称的转化. 2 诱导公式及和、差、倍角的三角函数——可以
实现角的形式的转化.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
升幂或降幂的转化,同时也可完成角的转化.
2 求值.常见的有给角求值,给值求值,给值求角.
①给角求值的关键是正确地分析角(已知角与未知角) 之间的关系,准确地选用公式,注意转化为特殊值. ②给值求值的关键是分析已知式与待求式之间角、 名称、结构的差异,有目的地将已知式、待求式的 一方或两方加以变换,找出它们之间的联系,最后 求待求式的值. ③给值求角的关键是求出该角的某一三角函数值, 讨论角的范围,求出该角.
【点评】本题从“幂”入手,借助倍角公式的变形公式,即降 幂公式先降幂再进行其他化简,这种化高次为低次是三角变换 的常用方法.
二
恒等变换下的拆角求值
2 π 1 π 【例 2】(1)已知 tan(α+β)= ,tan(β- )= ,求 tan( +α) 5 4 4 4 的值; sin7° +cos15°sin8° · (2) =__________. cos7° -sin15° sin8°
三
恒等变换下的三角证明
3π π 2-2sinα+ cosα+ 4 4 1+tanα 【例 3】证明: = . 4 4 cos α-sin α 1-tanα
π 2-2cos α+4 【证明】左边= cos2α-sin2α
2
π 2sin α+4 = 2 cos α-sin2α
2
π 1-cos2α+2 = cos2α-sin2α 1+sin2α = 2 cos α-sin2α
【点评】对于附加条件求值问题,要先看条件可不可以变形或 化简,然后看所求式子能否化简,再看它们之间的相互联系, 通过分析找到已知与所求的纽带.
素材1
1 化简:sin αsin β+cos αcos β- cos2αcos2β 的值为 2
2 2 2 2
1 2
.பைடு நூலகம்
1-cos2α 1-cos2β 1+cos2α 1+cos2β 1 【解析】原式= · + · - 2 2 2 2 2 cos2α· cos2β 1 1 = (1+cos2α· cos2β-cos2α-cos2β)+ (1+cos2α· cos2β 4 4 1 +cos2α+cos2β)- cos2αcos2β 2 1 = . 2
π π 【解析】(1)因为 +α=(α+β)-(β- ), 4 4 π π 所以 tan( +α)=tan[(α+β)-(β- )] 4 4 π tanα+β-tanβ- 4 = π 1+tanα+β· tanβ- 4 2 1 - 5 4 = 2 1 1+ × 5 4 3 = . 22
5 所以 tanC=-tan(A+B)=- ,所以 C 为钝角, 2 所以△ABC 为钝角三角形.
3.在△ABC 中,3sinA+4cosB=6,3cosA+4sinB=1,则∠C 的大小为( π A. 6 π 5π C. 或 6 6 ) 5π B. 6 π 2π D. 或 3 3
【解析】由已知, 9sin2A+16cos2B+24sinAcosB=36,① 9cos2A+16sin2B+24sinBcosA=1,② 1 ①+②,得 25+24sin(A+B)=37,所以 sin(A+B)= , 2 1 π 5π 所以 sinC= ,C= 或 . 2 6 6
2θ 2θ
2. A,B,C 是△ABC 的三个内角,且 tanA,tanB 是方 程 3x2-5x+1=0 的两个实数根,则△ABC 是( A.钝角三角形 C.等腰三角形 B.锐角三角形 D.等边三角形 )
5 【解析】tanA+tanB= ,① 3 1 tanAtanB= ,② 3 tanA+tanB 所以 tan(A+B)= = 1-tanAtanB 5 = , 1 2 1- 3 5 3
2
7 = . 25
17π 7π 5π π 因为 <x< ,则 <x+ <2π, 12 4 3 4 π 4 故 sin( +x)=- , 4 5 π sin +x π 4 4 tan( +x)= =- , 4 π 3 cos +x 4 7 4 28 故原式= ×(- )=- . 25 3 75
sin15° +cos15° -8° sin8° (2)原式= cos15° -sin15° -8° sin8° 1-cos30° sin15°cos8° · = =tan15° = cos8° cos15° sin30° =2- 3.
【点评】进行三角变换的技巧是变角,即注意角的和、差、 倍、半、互余、互补关系根据实际情况对角进行“拆”或 “添”变形,这样可大大减少运算量.基本的解题规律为: 观察差异(或角、或函数、或运算),寻找联系(借助熟知的公 式、方法或技巧),综合分析,实现转化.
备选例题
等比数列 {an}中,a2=sinα+cosα,a3=1+sin2α,其 π 中 <α<π.求: 2 1 3 (1)2sin2α- cos4α+ 是数列{an}的第几项? 2 2 4 (2)若 tan(π-α)= ,求数列{an}的前 n 项和 Sn. 3
【解析】设数列{an}的公比为 q, a3 1+sin2α sinα+cosα2 则 q= = = =sinα+cosα, a2 sinα+cosα sinα+cosα a2 所以 a1= =1. q 所以 an=(sinα+cosα)n-1(n∈N*).
3 证明.它包括无条件的恒等式和附加条件恒等式
的证明.常用方法:从左推到右;从右推到左; 左右互推.
θ 4 θ 3 1.若 sin = ,cos = ,则 θ 是( 2 5 2 5 A.第一象限角 C.第三象限角
)
B.第二象限角 D.第四象限角
θ θ 24 【解析】因为 sinθ=2sin cos = >0, 2 2 25 7 cosθ=cos -sin =- <0, 2 2 25 所以 θ 在第二象限.
4 4 (2)由 tan(π-α)= ,得 tanα=- , 3 3 π 4 3 又 <α<π,所以 sinα= ,cosα=- , 2 5 5 1 1 n -1 所以 q=sinα+cosα= ,所以 an=( ) , 5 5 1n 1- 5 5 1 1 n-1 故 Sn = = - ×( ) . 1 4 4 5 1- 5
一
恒等变换下的化简求值
cos2x 的值. π 2cos +x· sinx 4
x x 【例 1】已知 sin -2cos =0,求 2 2
x x x 【解析】由 sin -2cos =0,得 tan =2, 2 2 2 4 所以 tanx= =- , 3 x 2 1-tan 2 cos2x-sin2x cosx+sinx cos2x 所以 = = = π sinx cosx-sinxsinx 2cos +x· sinx 4 4 1- 1+tanx 3 1 = = . 4 4 tanx - 3 x 2tan 2
素材2
sin2x+2sin2x π 3 17π 7π 若 cos( +x)= , <x< ,求 的值. 4 5 12 4 1-tanx
2sinxcosx1+tanx 【解析】原式= 1-tanx π =sin2x· tan( +x). 4 π π 而 sin2x=sin[2( +x)- ] 4 2 π =-cos2( +x) 4 π =-[2cos ( +x)-1] 4
素材3
sin2α+β sinβ 求证: -2cos(α+β)= . sinα sinα
sin[α+β+α] 2cosα+βsinα 【证明】 左边= - sinα sinα sinα+βcosα+cosα+βsinα-2cosα+βsinα = sinα sinα+βcosα-cosα+βsinα = sinα sinα+β-α sinβ = =sinα=右边. sinα 故等式成立.
4.求值: 3tan20° tan40° +tan20° +tan40° =
3
.
【解析】原式= 3tan20° tan40° +tan60° (1-tan20° tan40° ) = 3.
1+tanα 1 5.若 =2013,则 +tan2α= cos2α 1-tanα
2013
.
1+sin2α 1 【解析】 +tan2α= cos2α cos2α sinα+cosα2 = cosα+sinαcosα-sinα cosα+sinα 1+tanα = = =2013. cosα-sinα 1-tanα
sin2α+cos2α+2sinαcosα = cos2α-sin2α cosα+sinα2 = cosα-sinαcosα+sinα cosα+sinα = cosα-sinα 1+tanα = =右边. 1-tanα 故等式成立.
【点评】观察左右两边式子间的差异,选择“从左证到右”, 利用凑角、降幂“1”的巧妙代换,将异角化为同角,高次化为 低次,最后弦化切,统一三角名称.
三角恒等变形的实质是对角、函数名称及运算结 构的转化,而转化的依据就是一系列的三角公式, 因此对三角公式在实现这种转化中的应用应有足 够的了解:
1同角三角函数关系——可实现函数名称的转化. 2 诱导公式及和、差、倍角的三角函数——可以
实现角的形式的转化.
3 倍角公式及其变形公式——可实现三角函数的
能运用同角三角函数的基本关系、 诱导公式、两角和与差的三角公式 进行简单的三角恒等变换.
三角变换的基本题型 — —化简、求值和证明
1 化简.
三角函数式化简的一般要求:三角函数种数尽量 少;项数尽量少;次数尽量低;尽量使分母不含 三角函数式;尽量使被开方数不含三角函数式; 能求出的值应尽量求出值. 依据三角函数式的结构特点,常采用的变换方法: 异角化同角;异名化同名;异次化同次;高次降次.
1 3 (1)2sin2α - cos4α+ 2 2 1 = ×(4sin2α-cos4α+3) 2 1 = [4sin2α-(1-2sin22α)+3] 2 1 = (2sin22α+4sin2α+2) 2 =(1+sin2α)2 =(sinα+cosα)4 =a5, 1 3 所以 2sin2α- cos4α+ 是数列{an}中的第 5 项. 2 2
2 求值.常见的有给角求值,给值求值,给值求角.
①给角求值的关键是正确地分析角(已知角与未知角) 之间的关系,准确地选用公式,注意转化为特殊值. ②给值求值的关键是分析已知式与待求式之间角、 名称、结构的差异,有目的地将已知式、待求式的 一方或两方加以变换,找出它们之间的联系,最后 求待求式的值. ③给值求角的关键是求出该角的某一三角函数值, 讨论角的范围,求出该角.
【点评】本题从“幂”入手,借助倍角公式的变形公式,即降 幂公式先降幂再进行其他化简,这种化高次为低次是三角变换 的常用方法.
二
恒等变换下的拆角求值
2 π 1 π 【例 2】(1)已知 tan(α+β)= ,tan(β- )= ,求 tan( +α) 5 4 4 4 的值; sin7° +cos15°sin8° · (2) =__________. cos7° -sin15° sin8°
三
恒等变换下的三角证明
3π π 2-2sinα+ cosα+ 4 4 1+tanα 【例 3】证明: = . 4 4 cos α-sin α 1-tanα
π 2-2cos α+4 【证明】左边= cos2α-sin2α
2
π 2sin α+4 = 2 cos α-sin2α
2
π 1-cos2α+2 = cos2α-sin2α 1+sin2α = 2 cos α-sin2α
【点评】对于附加条件求值问题,要先看条件可不可以变形或 化简,然后看所求式子能否化简,再看它们之间的相互联系, 通过分析找到已知与所求的纽带.
素材1
1 化简:sin αsin β+cos αcos β- cos2αcos2β 的值为 2
2 2 2 2
1 2
.பைடு நூலகம்
1-cos2α 1-cos2β 1+cos2α 1+cos2β 1 【解析】原式= · + · - 2 2 2 2 2 cos2α· cos2β 1 1 = (1+cos2α· cos2β-cos2α-cos2β)+ (1+cos2α· cos2β 4 4 1 +cos2α+cos2β)- cos2αcos2β 2 1 = . 2
π π 【解析】(1)因为 +α=(α+β)-(β- ), 4 4 π π 所以 tan( +α)=tan[(α+β)-(β- )] 4 4 π tanα+β-tanβ- 4 = π 1+tanα+β· tanβ- 4 2 1 - 5 4 = 2 1 1+ × 5 4 3 = . 22
5 所以 tanC=-tan(A+B)=- ,所以 C 为钝角, 2 所以△ABC 为钝角三角形.
3.在△ABC 中,3sinA+4cosB=6,3cosA+4sinB=1,则∠C 的大小为( π A. 6 π 5π C. 或 6 6 ) 5π B. 6 π 2π D. 或 3 3
【解析】由已知, 9sin2A+16cos2B+24sinAcosB=36,① 9cos2A+16sin2B+24sinBcosA=1,② 1 ①+②,得 25+24sin(A+B)=37,所以 sin(A+B)= , 2 1 π 5π 所以 sinC= ,C= 或 . 2 6 6
2θ 2θ
2. A,B,C 是△ABC 的三个内角,且 tanA,tanB 是方 程 3x2-5x+1=0 的两个实数根,则△ABC 是( A.钝角三角形 C.等腰三角形 B.锐角三角形 D.等边三角形 )
5 【解析】tanA+tanB= ,① 3 1 tanAtanB= ,② 3 tanA+tanB 所以 tan(A+B)= = 1-tanAtanB 5 = , 1 2 1- 3 5 3
2
7 = . 25
17π 7π 5π π 因为 <x< ,则 <x+ <2π, 12 4 3 4 π 4 故 sin( +x)=- , 4 5 π sin +x π 4 4 tan( +x)= =- , 4 π 3 cos +x 4 7 4 28 故原式= ×(- )=- . 25 3 75
sin15° +cos15° -8° sin8° (2)原式= cos15° -sin15° -8° sin8° 1-cos30° sin15°cos8° · = =tan15° = cos8° cos15° sin30° =2- 3.
【点评】进行三角变换的技巧是变角,即注意角的和、差、 倍、半、互余、互补关系根据实际情况对角进行“拆”或 “添”变形,这样可大大减少运算量.基本的解题规律为: 观察差异(或角、或函数、或运算),寻找联系(借助熟知的公 式、方法或技巧),综合分析,实现转化.
备选例题
等比数列 {an}中,a2=sinα+cosα,a3=1+sin2α,其 π 中 <α<π.求: 2 1 3 (1)2sin2α- cos4α+ 是数列{an}的第几项? 2 2 4 (2)若 tan(π-α)= ,求数列{an}的前 n 项和 Sn. 3
【解析】设数列{an}的公比为 q, a3 1+sin2α sinα+cosα2 则 q= = = =sinα+cosα, a2 sinα+cosα sinα+cosα a2 所以 a1= =1. q 所以 an=(sinα+cosα)n-1(n∈N*).
3 证明.它包括无条件的恒等式和附加条件恒等式
的证明.常用方法:从左推到右;从右推到左; 左右互推.
θ 4 θ 3 1.若 sin = ,cos = ,则 θ 是( 2 5 2 5 A.第一象限角 C.第三象限角
)
B.第二象限角 D.第四象限角
θ θ 24 【解析】因为 sinθ=2sin cos = >0, 2 2 25 7 cosθ=cos -sin =- <0, 2 2 25 所以 θ 在第二象限.
4 4 (2)由 tan(π-α)= ,得 tanα=- , 3 3 π 4 3 又 <α<π,所以 sinα= ,cosα=- , 2 5 5 1 1 n -1 所以 q=sinα+cosα= ,所以 an=( ) , 5 5 1n 1- 5 5 1 1 n-1 故 Sn = = - ×( ) . 1 4 4 5 1- 5
一
恒等变换下的化简求值
cos2x 的值. π 2cos +x· sinx 4
x x 【例 1】已知 sin -2cos =0,求 2 2
x x x 【解析】由 sin -2cos =0,得 tan =2, 2 2 2 4 所以 tanx= =- , 3 x 2 1-tan 2 cos2x-sin2x cosx+sinx cos2x 所以 = = = π sinx cosx-sinxsinx 2cos +x· sinx 4 4 1- 1+tanx 3 1 = = . 4 4 tanx - 3 x 2tan 2
素材2
sin2x+2sin2x π 3 17π 7π 若 cos( +x)= , <x< ,求 的值. 4 5 12 4 1-tanx
2sinxcosx1+tanx 【解析】原式= 1-tanx π =sin2x· tan( +x). 4 π π 而 sin2x=sin[2( +x)- ] 4 2 π =-cos2( +x) 4 π =-[2cos ( +x)-1] 4
素材3
sin2α+β sinβ 求证: -2cos(α+β)= . sinα sinα
sin[α+β+α] 2cosα+βsinα 【证明】 左边= - sinα sinα sinα+βcosα+cosα+βsinα-2cosα+βsinα = sinα sinα+βcosα-cosα+βsinα = sinα sinα+β-α sinβ = =sinα=右边. sinα 故等式成立.
4.求值: 3tan20° tan40° +tan20° +tan40° =
3
.
【解析】原式= 3tan20° tan40° +tan60° (1-tan20° tan40° ) = 3.
1+tanα 1 5.若 =2013,则 +tan2α= cos2α 1-tanα
2013
.
1+sin2α 1 【解析】 +tan2α= cos2α cos2α sinα+cosα2 = cosα+sinαcosα-sinα cosα+sinα 1+tanα = = =2013. cosα-sinα 1-tanα
sin2α+cos2α+2sinαcosα = cos2α-sin2α cosα+sinα2 = cosα-sinαcosα+sinα cosα+sinα = cosα-sinα 1+tanα = =右边. 1-tanα 故等式成立.
【点评】观察左右两边式子间的差异,选择“从左证到右”, 利用凑角、降幂“1”的巧妙代换,将异角化为同角,高次化为 低次,最后弦化切,统一三角名称.
三角恒等变形的实质是对角、函数名称及运算结 构的转化,而转化的依据就是一系列的三角公式, 因此对三角公式在实现这种转化中的应用应有足 够的了解:
1同角三角函数关系——可实现函数名称的转化. 2 诱导公式及和、差、倍角的三角函数——可以
实现角的形式的转化.
3 倍角公式及其变形公式——可实现三角函数的
能运用同角三角函数的基本关系、 诱导公式、两角和与差的三角公式 进行简单的三角恒等变换.
三角变换的基本题型 — —化简、求值和证明
1 化简.
三角函数式化简的一般要求:三角函数种数尽量 少;项数尽量少;次数尽量低;尽量使分母不含 三角函数式;尽量使被开方数不含三角函数式; 能求出的值应尽量求出值. 依据三角函数式的结构特点,常采用的变换方法: 异角化同角;异名化同名;异次化同次;高次降次.
1 3 (1)2sin2α - cos4α+ 2 2 1 = ×(4sin2α-cos4α+3) 2 1 = [4sin2α-(1-2sin22α)+3] 2 1 = (2sin22α+4sin2α+2) 2 =(1+sin2α)2 =(sinα+cosα)4 =a5, 1 3 所以 2sin2α- cos4α+ 是数列{an}中的第 5 项. 2 2
