深圳大学 硕士研究生课程教学大纲
教育硕士教育原理课程教学大纲

教育硕士教育原理课程教学大纲教育硕士教育原理课程教学大纲一、课程简介1.1 课程名称:教育原理1.2 学时数:36学时1.3 学分数:2学分1.4 授课对象:教育硕士研究生1.5 课程性质:必修课程二、课程教学目标2.1 理解教育的本质、目的和价值;2.2 理解现代人类教育的历史演化和主流教育思想;2.3 掌握教育学的基本理论和知识体系;2.4 理解并能够分析当代中国教育的现状和问题;2.5 培养教育研究的兴趣和能力,为后续专业学习和实践打下基础。
三、课程内容和教学方法3.1 教育的本质、目的和价值3.1.1 教育的概念及其本质3.1.2 教育的目的和价值3.1.3 教育的主要内容和形式3.1.4 教育与发展的关系3.1.5 学科教育与综合素质教育教学方法:授课、讨论、案例分析3.2 现代人类教育的历史演化和主流教育思想 3.2.1 西方教育思想的发展3.2.2 东方教育思想的传统和现代发展3.2.3 当代主流教育思想的特点和发展趋势教学方法:授课、讨论、文献阅读3.3 教育学的基本理论和知识体系3.3.1 教育学的概念、对象和范畴3.3.2 教育学的基本理论和原则3.3.3 教育学的分支学科及其研究内容3.3.4 教育学研究的方法和规律教学方法:授课、讨论、文献阅读3.4 当代中国教育的现状和问题3.4.1 当代中国教育的历史演进和主要成就 3.4.2 当前中国教育的发展趋势和面临的挑战 3.4.3 当代中国教育改革的重大问题和对策教学方法:授课、讨论、文献阅读四、考核方式和成绩评定4.1 考核方式:闭卷笔试4.2 考核内容:课程基本理论和知识体系4.3 成绩评定:平时成绩(20%)+笔试成绩(80%)。
硕士研究生课程教学大纲

硕士研究生课程教学大纲深圳大学硕士研究生课程教学大纲课程名称与编号金融数学(The Mathematics of Finance)适用专业应用数学先修课程概率、统计教学方式讲授一、课程设置的指导思想20世纪90年代以来,数学、金融、计算机以及全球经济呈现融合趋势,货币市场中,诸如期权、互换、交叉货币证券等复杂金融工具的交易非常普遍,鉴于金融界被大量丰富的数学工具和模型所困扰,运用金融数学的思想和模式对大量的市场交易活动进行分析、计算、预测就尤显重要。
二、教学的基本要求通过学习本课程内容,要求读者能够掌握金融期货期权理论的具体运用,能对部分数量的金融产品交易的实例展开分析,并以这些方法为线索展开深入学习和分析研究。
三、教学内容(可以提出各章节的教学目的或要求)第1章导言(Introduction)§1.1 金融市场与数学§1.2 股票及其衍生产品§1.3 期货合约定价§1.4 债券市场§1.5 利率期货§1.6 外汇第2章二叉树、资产组合复制和套利§2.1 衍生产品定价的三种方法§2.2 博弈论方法§2.3 资产组合复制§2.4 概率方法§2.5 风险§2.6 多期二叉树和套利第3章股票与期权的二叉树模型§3.1 股票价格模型§3.2 用二叉树模型进行看涨§3.3 美式期权定价§3.4 一类奇异期权——敲出期权的定价§3.5 奇异期权——回望期权定价§3.6 实证数据下二叉树模型分析§3.7 N期二叉树模型的定价和对冲风险第4章用表单计算股票和期权的价格二叉树§4.1 表单的基本概念§4.2 计算欧式期权二叉树§4.3 计算美式期权价格二叉树§4.4 计算障碍期权二叉树§4.5 计算N期二叉树第5章连续时间模型和Black-Scholes公式§5.1 连续时间股票模型§5.2 离散模型§5.3 Black-Scholes公式§5.4 看涨期权与看跌期权平价§5.5 几何布朗运动股价模型应用第6章Black-Scholes模型的解析方法§6.1 微分方程推导的思路§6.2 V(S,t)的扩展§6.3 Black-Scholes微分方程求解方法§6.4 期货期权第7章对冲§7.1 德尔塔对冲§7.2 股票或资产组合的对冲方法§7.3 隐含波动率§7.4 德尔塔对冲法则的推导§7.5 购买股票后的德尔塔对冲第8章债券模型和利率期权§8.1 利率和远期利率§8.2 零息券§8.3 互换§8.4 债券价格§8.5 HJM之谜的推导第9章债券价格计算方法§9.1 债券价格的二叉树模型§9.2 二项式的Vzsicek模型:均值反转模型第10章货币市场和外汇风险§10.1 交易机制§10.2 远期货币:利率平价§10.3 外汇期权§10.4 保证汇率(GER)和交叉货币证券§10.5 是否套期保值与套期保值数量的决定第11章国际政治风险分析§11.1 国际风险的种类§11.2 信用衍生产品与政治风险§11.3 国际政治风险的定价§11.4 决定风险溢价的两个模型§11.5 一个JLT模型的假想例子五、主要教材和参考文献J.Stampfli: 金融数学六、考试方式考试执笔人:高智民审核人:年月日。
深圳大学课程教学大纲

深圳大学课程教学大纲课程编号: 2215191001/02/03 课程名称: 微机原理与接口技术开课院系: 计算机与软件学院软件工程系制订(修订)人: 卢亚辉、李炎然审核人: 黄强批准人:明仲2010年3月4日制(修)订课程名称:微机原理与接口技术英文名称: Principles of Microcomputer and Interface总学时: 72 其中:实验课 18 学时学分: 3.5先修课程: 数字电路教材:微型计算机技术及应用(第3版),戴梅萼等,清华大学出版社, 2003参考教材:[1] The 80x86 IBM PC AND COMPATIBLE COMPUTERS, Muhammad Ali Mazidi Janice Gillispie Mazidi,清华大学出版社,2004[2] 微机原理与接口技术实验指导书,薛丽萍,深圳大学教材中心[3] 微机原理与接口技术(第二版),龚尚福,西安电子科技大学出版社,出版日期 2008-08.课程性质: □综合必修■专业必修□专业选修□全校公选教学目标:使学生掌握微型计算机的基本工作原理,掌握微机接口技术及编程技术。
学生在完成本课程学习后,应能够:(1)掌握微型计算机的工作原理、8086CPU的内部结构(2)掌握8086CPU指令系统和汇编语言的基本编程方法,掌握基本操作技能和汇编语言程序上机、调试、运行能够独立编写基于80x86的汇编程序(3)掌握熟悉存储器系统的结构,能够进行地址编码及译码电路设计和程序设计(4)掌握输入/输出技术,能够进行可编程并行I/O接口器8255A 的编程使用(5)掌握定时器/计数器的编程使用(6)掌握中断概念,能对8259A可编程中断控制器进行编程使用(7)掌握串行通信概念,能使用8251器件进行串行通信设计(8)了解CPU与外设之间的数据传送方式(程序方式、中断方式、DMA方式)(9)了解键盘显示接口技术课程简介:该课程是计算机系统的核心课程,是计算机技术的基础。
深圳大学 复分析硕士研究生教学大纲

及形式
讲授、讨论
学时分配
进度安排
1.Cauchy定理(10学时);
2.Cauchy型积分(8学时);
3.最大模原理(8学时);
4.共形映射(8学时);
5.解析函数的零点(8学时);
6.解析延拓(6学时);
7.单叶函数(12学时)。
教材
作者:Walter Rudin.
书名:Real and Complex Analysis(Third Edition).
附件四:
硕士研究生课程教学大纲
授课教师
张文俊
性别
男
职称
教授
所在单位
师范学院数学系
授课对象
应用数学专业、应用复分析方向硕士研究生
授课名称
复分析
授课时数
60
课程类别Hale Waihona Puke 学位√必修选修考试方式
考试√考查
课
程
目
标
本课程是大学《复变函数》课程的深入与扩展,为应用复分析的研究工作打下坚实的基础。
教
学
内
容
1.Cauchy定理。包括同伦形式的Cauchy定理、同调形式的Cauchy定理等;
版权:Copy right 1987,1974,1966 by th McGraw-Hill Companies, Inc.
印刷:Printed by China Machine Press (机械工业出版社),2004.01。
必
读
书
目
1.钟玉泉.复变函数论(第二版),高等教育出版社,2000年。
2.龚升.简明复分析,北京大学出版社,1996年。
2.作为一个复变量的复变函数与作为两个实变量的二元实函数对构成的映射,二者在连续性、导数定义等方式上相同,但为什么复变量函数具有更好的性质?其根本原因在哪里?
深圳大学高等教育学专业硕士研究生培养方案-深圳大学高等教育研究所

【人才培养】一、培养目标本专业立足经济特区背景,培养适应高等教育改革与发展需要,掌握扎实、系统的高等教育理论知识,具有健全的人格、较强的创新精神和独立工作能力,能胜任高等教育科学研究与教学工作及高等教育管理工作,德、智、体全面发展的高级专门人才。
二、研究方向本学科包括高等教育管理和高等教育理论两个主要研究方向。
1. 高等教育管理研究方向,着重研究高等教育政策、高等教育管理、高等教育评估与战略、高等教育投资与效益,特别是研究广东省、深圳市及市内高等院校的高教改革与发展问题,研究和比较深港高等教育政策与投资问题,为有关部门的高等教育决策提供咨询和建议。
2. 高等教育理论研究方向,着重研究高等教育基本原理和中国高等教育改革与发展的若干重大理论问题,研究高等教育学科建设的相关理论,探讨高等教育的本质和规律,考察中外高等教育发展的现状和历史,探索建立具有中国特色的高等教育理论体系。
三、学习年限本学科的硕士研究生的培养实行弹性学制,学习年限一般为3年,最长不超过5年。
若研究生学位课平均成绩达到85分以上、指导教师确认有能力提前完成学位论文,可申请提前半年毕业。
四、培养方式本学科实行以导师负责和指导小组集体培养相结合,充分利用校内外学术资源的开放式培养方式,课程学习和科学研究(论文工作、社会实践)相结合,课程学习与科学研究并重,在研究中学习。
硕士研究生在校期间,应在公开发行的学术刊物上至少发表一篇与专业相关的学术论文(第一作者或以导师为第一作者的第二作者,第三及其后作者名次一律不计),或完成相当水平的研究报告、政策咨询报告,或取得相当水平的科研成果。
在课程学习结束后,进行研究生中期考核,中期考核通过方可进入学位论文工作阶段。
深圳大学高等教育学专业硕士研究生培养方案一、课程设置本学科硕士研究生的课程分为学位课程和非学位课程。
其中,学位课程分为公共学位课程和专业学位课程两类,均为必修课;非学位课程包括必修课、选修课和补修课三类。
深圳大学 计算机辅助几何设计课程教学大纲

深圳大学硕士研究生课程教学大纲课程名称与编号计算机辅助几何设计(Computer-AidedGeometric Design)适用专业应用数学先修课程应用数学本科课程教学方式面授一、课程设置的指导思想(包括课程性质\类别\总的教学目的和要求)使应用数学系硕士生系统掌握计算几何中的几种主要的数学方法,为其提供从事计算机辅助设计、计算机图形学研究之需要。
二、教学的基本要求本课程拟在学习计算几何的基本知识,重点学习工业产品形状描述的数学方法,主要内容有:曲线曲面的基本理论、参数样条曲线曲面、Bézier曲线曲面、几何连续性、B样条曲线曲面、NURBS曲线曲面、COONS曲面等内容。
三、教学内容(可以提出各章节的教学目的或要求)第1章曲线和曲面的基本理论§1.1 概述§1.2 曲线曲面的参数表示§1.3 曲线论§1.4 曲面论§1.5 曲线曲面表示的几何不变性第2章参数多项式插值与逼近§2.1 基本概念§2.2 多项式插值曲线§2.3 张量积曲面§2.4 曲面的参数化第3章参数样条曲线曲面§3.1参数连续性§3.2 参数样条曲线§3.3 参数样条曲线的光顺性§3.4 参数双三次样条曲面第4章Bézier曲线曲面§4.1 Bézier曲线及其性质§4.2 Bézier曲面第5章几何连续性§5.1参数曲线的几何连续性§5.2 参数曲面的几何连续性第6章B样条曲线§6.1 B样条与B样条曲线的基本概念§6.2 均匀B样条§6.3 非均匀B样条第7章B样条曲面§7.1 B样条曲面的概念§7.2 B样条曲面的性质第8章有理B样条曲线§8.1 NURBS方法的提出及优缺点§8.2 NURBS曲线的性质第9章有理B样条曲面§9.1 NURBS曲面的概念§9.2 NURBS曲面的性质四、课时分配五、主要教材和参考文献1.An Introduction to the Curves and Surfaces of Computer-Aided Design, Robert C. Beach V AN NOSTRAND REINHOLD, New York.2.《计算机辅助几何设计与非均匀有理B样条》施法中著北京航空航天大学出版社1994,10。
深圳大学927学前教育学2021年考研专业课初试大纲

深圳大学2021年硕士研究生入学考试大纲、参考书目
(初试科目只提供考试大纲,复试科目只提供参考书目)
命题学院/部门(盖章):师范学院(教育学部)
考试科目代码及名称:[927]学前教育学
一、考试基本要求
本考试大纲适用于报考深圳大学教育硕士专业的硕士研究生入学考试。
《学前教育学》是为招收教育硕士而设置的具有选拔功能的水平考试。
它的主要目的是测试考生对于学前教育的基本知识与技能的掌握程度。
要求考生掌握学前教育学的基本概念和基本理论,并能够理论联系实际,具有进行园本课程开发、教学创新和解决现实教学问题的能力。
二、考试内容和考试要求
(一)学前教育学的对象、任务及发展
1.熟悉学前教育学的对象、任务及发展
2.认识这门科学的现状和基本的理论问题,了解今后研究的方向。
(二)学前教育与社会的关系
1.熟悉学前教育的产生和发展
2.熟悉学前教育与社会经济、政治、文化等方面的关系
(三)学前教育和儿童身心发展的关系
1.理解学前教育和其他因素在儿童发展中的作用。
矩阵理论课程教学大纲-深圳大学研究生院
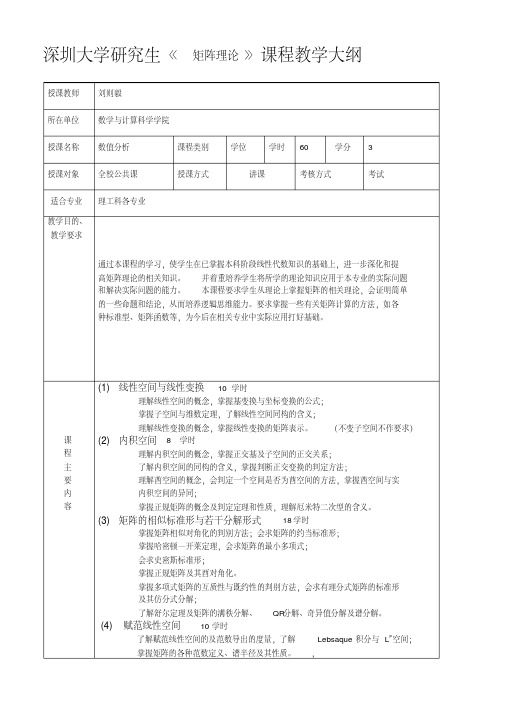
深圳大学研究生《矩阵理论》课程教学大纲授课教师刘则毅所在单位数学与计算科学学院授课名称数值分析课程类别学位学时60 学分 3授课对象全校公共课授课方式讲课考核方式考试适合专业理工科各专业教学目的、教学要求通过本课程的学习,使学生在已掌握本科阶段线性代数知识的基础上,进一步深化和提高矩阵理论的相关知识。
并着重培养学生将所学的理论知识应用于本专业的实际问题和解决实际问题的能力。
本课程要求学生从理论上掌握矩阵的相关理论,会证明简单的一些命题和结论,从而培养逻辑思维能力。
要求掌握一些有关矩阵计算的方法,如各种标准型、矩阵函数等,为今后在相关专业中实际应用打好基础。
课程主要内容(1) 线性空间与线性变换 10学时理解线性空间的概念,掌握基变换与坐标变换的公式;掌握子空间与维数定理,了解线性空间同构的含义;理解线性变换的概念,掌握线性变换的矩阵表示。
(不变子空间不作要求)(2) 内积空间 8学时理解内积空间的概念,掌握正交基及子空间的正交关系;了解内积空间的同构的含义,掌握判断正交变换的判定方法;理解酋空间的概念,会判定一个空间是否为酋空间的方法,掌握酋空间与实内积空间的异同;掌握正规矩阵的概念及判定定理和性质,理解厄米特二次型的含义。
(3) 矩阵的相似标准形与若干分解形式18学时掌握矩阵相似对角化的判别方法;会求矩阵的约当标准形;掌握哈密顿—开莱定理,会求矩阵的最小多项式;会求史密斯标准形;掌握正规矩阵及其酉对角化。
掌握多项式矩阵的互质性与既约性的判别方法,会求有理分式矩阵的标准形及其仿分式分解;了解舒尔定理及矩阵的满秩分解、QR分解、奇异值分解及谱分解。
(4) 赋范线性空间10学时了解赋范线性空间的及范数导出的度量,了解Lebsaque积分与L p空间;掌握矩阵的各种范数定义、谱半径及其性质。
,(5) 矩阵函数及其应用6学时理解向量范数、矩阵范数及向量和矩阵的极限的概念;掌握矩阵幂级数收敛的判定方法,会求矩阵函数;会求矩阵的微分与积分;了解矩阵函数在线性系统理论中的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
硕士研究生课程教学大纲
授课教师
张文俊性别Leabharlann 男职称教授
所在单位
师范学院数学系
授课对象
应用数学专业、应用复分析方向硕士研究生
授课名称
复解析动力系统
授课时数
40
课程类别
学位必修选修√
考试方式
考试√考查
课
程
目
标
介绍单复变解析函数迭代理论的基本概念、基本原理、基本方法、基本结论和最新前沿发展情况;介绍多复变全纯映射迭代理论的基本背景知识和方法。为学生从事复解析动力系统的研究奠定基础。
思
考
讨
论
题
1.从单位圆盘上解析自映射的动力学性质能否给出一般单连通区域上的动力学性质?
2.周期点在动力系统中扮演着什么角色?为什么周期点如此重要?
多复变全纯映射迭代理论的基本背景知识和方法。
教学方法
及形式
讲授、讨论
学时分配
进度安排
1.复解析动力系统的起源、基本问题、基本方法与分类,单位圆盘上解析自映射的动力学性质(8学时);
2.有理函数的动力系统:周期点、临界点、Fatou集、Julia集的基本概念与基本性质(10学时);
3.Fatou集的结构(12学时);
4.多复变全纯映射迭代理论的基本背景知识和方法(10学时)。
教材
作者:Alan F. Beardon.
书名:Iteration of Rational Functions__Complex Analytic Dynamical Systems.
版权:Copy right 1991bySpringer-Verlag New York,Inc.
教
学
内
容
1.复解析动力系统的起源、基本问题、基本方法与分类,单位圆盘上解析自映射的动力学性质;
2.有理函数的动力系统:周期点、临界点、Fatou集、Julia集的基本概念与基本性质;
3.Fatou集的结构;
4.多复变全纯映射迭代理论的基本背景知识和方法。
教
学
要
点
单位圆盘上解析自映射的动力学性质;
有理函数的动力系统中周期点的分类、Fatou集的结构、Julia集刻划;
印刷:Printedin the United States of Americ。
必
读
书
目
1.钟玉泉.复变函数论(第二版),高等教育出版社,2000年。
2.龚升.简明复分析,北京大学出版社,1996年。
参
考
文
献
目
录
1.任福尧主编.复解析动力系统,复旦大学出版社,1997年。
2.吕以撵.复动力系统引论,科学出版社,1991年。
