内非保守力做负功的例子
保守力做功公式(一)

保守力做功公式(一)保守力做功公式在物理学中, 保守力做功公式是一个重要的概念。
保守力是指做功与路径无关的力,而做功则是力对物体做的功。
在这篇文章中,将介绍保守力做功公式以及一些相关的公式,并通过举例进行解释说明。
保守力和非保守力•保守力:保守力是指在特定路径下,力所做的功与路径无关。
它只与起点和终点的位置有关。
例如,重力和弹簧力都是保守力。
保守力与势能(potential energy)密切相关。
•非保守力:非保守力是指在特定路径下,力所做的功与路径有关。
摩擦力和空气阻力都是非保守力。
非保守力导致系统的机械能发生改变。
保守力做功公式保守力做功公式可以表示为:W=−ΔU其中: - W表示力所做的功; -ΔU表示势能的变化。
根据这个公式,如果势能增加,力所做的功为负;如果势能减少,力所做的功为正。
示例示例 1:重力做功考虑一个物体沿直线向上抛掷并上升到最高点。
在上升过程中,重力对物体做的功为负。
我们可以使用保守力做功公式来计算。
假设物体的质量为m,上升的高度为h,重力加速度为g。
在最高点,物体的势能为0。
因此,势能的变化为ΔU=−mgℎ其中h为负值。
根据保守力做功公式,重力对物体做的功为W=−(−mgℎ)=mgℎ可以看到,重力对物体做的功为正,这也符合我们的直觉。
物体上升时,重力做正功,输给了物体。
示例 2:弹簧力做功考虑一个弹簧振子,当振子从一个最大幅度位置经过过盪点后,达到另一个最大幅度位置。
在振子的运动过程中,弹簧力对振子做的功既正也负。
假设振子相对过盪点的位移为x,弹簧的劲度系数为k。
在过盪点,势能为0。
因此,势能的变化为ΔU=−12kx2根据保守力做功公式,弹簧力对振子做的功为W=−(−12kx2)=12kx2可以看到,当振子从最大幅度位置向过盪点运动时,弹簧力对振子做的功为正;当振子从过盪点向最大幅度位置运动时,弹簧力对振子做的功为负。
这也符合我们对弹簧振子运动过程的直观理解。
总结在这篇文章中,我们介绍了保守力做功公式以及与之相关的概念。
质点系的功能原理公式

质点系的功能原理公式你想啊,质点系是啥呢?就好比是一群小伙伴,每个小伙伴就是一个质点啦。
那功能原理就是在说这些小伙伴们的能量和做功之间的关系。
再讲讲W_内非保,这是质点系内非保守力做的功。
啥是非保守力呢?就像摩擦力这种,它做的功可不像重力做功那样有个比较固定的规律。
在质点系里,如果小伙伴们之间互相有摩擦之类的非保守力,那这个摩擦做的功就是W_内非保。
比如说,小推车里放了几个小木块,小木块之间互相摩擦,这个摩擦做的功就是内部的非保守力做的功。
那E_2-E_1呢?这就是质点系末状态的机械能减去初状态的机械能。
机械能就是动能和势能的总和。
就好比小伙伴们一开始有一定的能量,玩了一会儿之后呢,能量就变了。
比如说一开始小推车和小木块静止在一个小坡上,有一定的重力势能,然后推了一下动起来了,动能和势能都变了,这个前后能量的差值就是E_2-E_1。
你看这个公式啊,它特别能说明问题。
如果外力对质点系做正功,同时内部非保守力做的功也合适,那质点系的机械能就会增加。
就像有个神仙在外面给小推车助力,小推车里的小木块之间的摩擦也不大,那小推车这个质点系就会跑得更快,能量就增加了。
要是外力做负功,内部非保守力又消耗很多能量,那机械能就减少。
就好比小推车被人往后拉,小木块之间还摩擦得厉害,那小推车的能量就越来越少啦。
这个公式在生活里也有好多例子呢。
比如说咱们骑自行车,人蹬自行车的力就是外力,自行车链条和齿轮之间的摩擦就是内部非保守力。
如果人蹬得很带劲,链条摩擦又小,那自行车就会跑得飞快,机械能增加,也就是动能增加啦。
要是人不蹬了,链条还卡得死死的,那自行车就会慢慢停下来,机械能减少。
还有啊,在游乐场玩那种水上碰碰船。
发动机推动船走的力是外力,船和水之间的摩擦以及船里面的一些部件摩擦就是内部非保守力。
要是发动机给力,摩擦又小,那船就可以在水面上欢快地跑来跑去,能量满满。
要是发动机坏了,摩擦还大,那船就只能慢慢停在水上,能量越来越少啦。
3-5 保守力和非保守力
保守力 重 力 弹 力
势能(E p ) mgh
1 2
势能零点 h=0
Ep
0
势能曲线 h
Ep
kx
2
x=0
Ep
0 0
x r
引 力
mM G r
r=∞
3.势能和保守力的关系: 势能是保守力对路径的线积分,EP=
dEP F dl F cos dl Fdl l
dE P Fl dl
Mm 1 EP= r -G r 2 dr GMm r
F m r
M
o
③弹性势能
Wab
xb
xa
1 2 1 2 kxdx ( kxb kxa ) EP 2 2
弹性势能以弹簧原长为零势能点。
1 1 2 E P kxdx (0 kx ) kx 2 x 2 2 势能曲线对照表(势能随位置变化的曲线~势能曲线)
m
C
L1
F
B
A
L2
D
WACB WADB F dr
ACB
ADB
F dr
(路径L1)
(路径L2)
对沿闭合路径ACBDA运动一周的物体做功为
W F dr
L ACB
F dr
BDA
F dr
BDA
保守力在 l 方向投影 E p 在 l 方向空间变化率
b
a
F dl
F
m
a
θ
dl
b
l
Fl
保守力沿某一给定的l方向的分量等于与此保守力 相应的势能函数沿l方向的空间变化率。 若势能为EP(x,y,z)
保守力与非保守力

非保守力:凡作功与路径有关的力称为非保守力。
常见的摩擦力,物体间相互作非弹性碰撞时的冲击力都属于非保守力。
非保守力具有沿任意闭合路径作功不等于零的特点.非保守力包括耗散力和非耗散力两类。
在力学范围内接触的非保守力大多数是耗散力,所以长期以来耗散力就成了非保守力的同义词.严格说来两者是有区别的,一个系统的总机械能减少,并转变为系统的热能或内能.通常人们把这个过程叫耗散过程,而把导致耗散的力成为耗散力。
摩擦力是耗散力,但非保守力(如爆炸力)不一定都是耗散力.⑴定义:做功多少只由始末位置所决定,而跟路径无关的力叫做保守力。
做功多少和物体运动路径有关的力叫耗散力。
⑵说明①保守力对物体做功的多少取决于物体始末位置,如果在该力作用下,物体的运动沿闭合路线绕行一周回到了起始位置,则所做功为零。
重力、弹力等属于保守力。
耗散力做功就不能由物体的始末位置决定,而和物体的运动路径有关,在其他条件相同的情况下,物体运动路径越长,所做的功也越多。
摩擦力、粘滞力等属于耗散力②保守力和耗散力所做功的情况不同,是和这两种力的本身的特点有关。
物体系确定后保守力和物体的运动状况无关,其大小由相互作用物体的相对位置所确定,它的方向总在两个相互作用物体的连线上。
例如,物体确定后,重力的大小决定于它离开地面的高度,方向竖直向下,而和物体以什么样的速度运动无关,和物体运动速度的大小和方向如何变化无关。
耗散力的大小和方向都随着物体运动速度的大小、方向的改变而发生变化。
例如,空气对运动物体的阻力,其方向随着物体运动的方向改变而变化,它的大小随物体运动速度增大而增加。
③保守力和物体系的势能有着极为密切的联系。
保守力做正功,则物体系的势能减少;反之,则物体系的势能增加。
而且相对两个位置之间,功量一定,能量差一定。
所以物体间存在保守力是物体系具有势能的条件。
系统的各物体在只受保守力作用的情况下其机械能守恒。
耗散力不象保守力,对于两个位置之间,力对物体做功没有确定的值,从而相应的两个位置之间没有一定的能量差。
保守力和非保守力-PPT课件

A
rA
r
rB
m
m'
B
4
( 2)
弹性力作功
设原长为坐标原点, 物体在F’外,位移: x ' F外 F
o
x
P
xபைடு நூலகம்
F d x kx i dx i kx 弹力: F kx i dW
1 2 1 2 ( kx k1 x ) W k x d x 2 dW x 1 2 2
mgy
Gm E g 2 RE
E
m y
Ep 0
取: E 0 有: E mgy p ,R E p ,R y
RE
)
15
重力势能: E mgy ( 取地面为零势点 p
谢谢大家!
16
1
一
万有引力和弹性力作功的特点
(1) 万有引力作功
m ' 对m 的万有引力为
m 'm F G 2 e r r
r时,F m 移动d 作元功为
A
r d r
r r
m
er
m'
B
m 'm G 2 e r d W F d r r d
r
2
m 'm d W F d r G 2 e r r d r
11
注意: 势能是状态的函数 E E ( x ,y ,z ) p p 是坐标的函数 势能具有相对性,与势能零点的选取有关.
通常取地面为重力势能的零点;取无穷远处为引力势 能的零点;取平衡位置处为弹性势能的零点。这样这 三种势能分别为:
重力势能: E p mgy
m m 引力势 E 能 G: p r 1 2 弹性势 E 能 : kx p 2 注意:如果另选势能零点,则势能的值就不能 用上式来计算了。
大物保守力简答题

大物保守力简答题
1. 什么是保守力?保守力做功的特点是什么?举例说明保守力和非保守力。
- 保守力是指做功只与质点的始末位置有关,与路径无关的力。
保守力做功的特点是可以用势能来表示,且沿任意闭合路径的环路功为零。
- 例如,重力、弹力、静电力等都是保守力,因为它们做功只取决于质点的高度、形变或电势差等位置因素,而与质点运动的具体轨迹无关。
非保守力是指做功不仅与质点的始末位置有关,还与路径有关的力。
非保守力做功不能用势能来表示,且沿任意闭合路径的环路功不为零。
- 例如,摩擦力、空气阻力、粘滞力等都是非保守力,因为它们做功不仅取决于质点的位移大小和方向,还取决于质点运动的速度、加速度和轨迹等因素。
2. 如何判断一个力是否为保守力?给出判断保守力的两种方法,并说明原理。
-判断一个力是否为保守力,有以下两种方法:
- 方法一:检验该力沿任意闭合路径做功是否为零。
如果为零,则该力为保守力;如果不为零,则该力为非保守力。
这是因为保守力做功只与始末位置有关,沿闭合路径回到原点时始末位置相同,所以做功为零;非保守力做功不仅与始末位置有关,还与路径有关,沿闭合路径回到原点时虽然始末位置相同,但路径不同,所
以做功不为零。
- 方法二:检验该力是否可以用一个标量函数(即势函数)来表示。
如果可以,则该力为保守力;如果不可以,则该力为非保守力。
这是因为保守力做功可以用势能来表示,而势能是一种状态量,只与位置有关,可以用一个标量函数来表示;非保守力做功不能用势能来表示,而与位置和路径都有关,不能用一个标量函数来表示。
保守力与非保守力
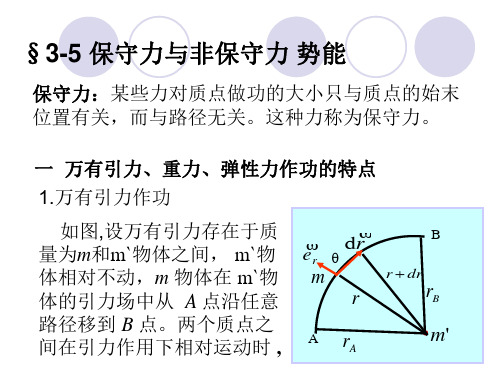
一、 万有引力、重力、弹性力作功的特点1 万有引力作功如上图所示,有两个质量为m m ' 和的质点,其中质点m ' 固定不动。
取m ' 的位置为坐标原点,A 、B 两点对m ' 的距离分别为m r r B A , 和经任一路径由点A 运动到点B ,万有引力作的功为)11(A B r r m m G W -'= (3-10)上式表明,当质点的质量m m ' 和均给定时,万有引力作的功只取决于质点m 的起始和终了的位置,而与所经过的路径无关。
这是万有引力作功的一个重要特点。
扩充内容:计算万有引力作的功设在某一时刻质点m 距质点m '的距离为r ,其位矢为r ,这时质点m 受到质点m '的万有引力为r 2e F r m m G '-=r e 为沿位矢r 的单位矢量,当m 沿路径移动位移元r d 时,万有引力作的功为r e r F d d d r 2⋅'-=⋅=r m m G W从图可以看出r d cos d cos d d r r ===⋅θθr r e r e于是,上式为r r m m G W d d 2'-=所以,质点m 从点A 沿任一路径到达点B 的过程中,万有引力作的功为⎰⎰'-==B A r r B A r r m m G W W 2d 1d即2 重力作功如右图所示,一个质量为m 的质点,在重力作用下从点A 沿ACB 路径至点B ,点A 和点B 距地面的高度分别为21 y y 和,计算重力作功为()12mgy mgy W --= (3-11)上式表明,重力作功只与质点的起始和终了位置有关,而与所经过的路径无关,这是重力作功的一个重要特点。
扩充内容: 计算重力作的功因为质点运动的路径为一曲线,所以重力和质点运动方向之间的夹角是不断变化的。
我们把路径ACB 分成许多位移元,在位移元r d 中,重力P 所作的功为r P d d ⋅=W若质点在平面内运动,按图所选坐标,并取地面上某一点为坐标原点O ,有j i r y x d d d +=且j P mg -=。
3-5保守力 势能
M1
M2
M1
F dr
上页 下页
W
W保 ( Ep 2 Ep1 ) Ep
比较:
W合 Ek 2 Ek1 Ek
注意:i、势能属于保守系,而不是属于一个物体;
ii、一个系统的势能与描述运动的参考系的选择无关,
系统在两个位形的势能差与零势点的选择无关.
上页
Ep
O
Ep
x
Ep
y
O
O
x
Mm Ep G r
引力势能曲线
Ep mgy
重力势能曲线
1 2 Ep kx 2
弹性势能曲线
上页
下页
1、保守力:如果力所做的功与路径无关,仅与始、末位置有关, 这样的力称为保守力. 例如:重力、万有引力、弹力、分子力 、静电力
L
F保 dr 0
这也是保守力的另外一种定义.
2、非保守力:做功与路径有关的力称为非保守力.
L
F非保 dr 0
例如: 摩擦力
3、保守力场:如果质点在某个空间内任何位置,都受到一个 大小和方向完全确定的保守力的作用,称这部分空间中存在着 保守力场. 例如: 重力场、万有引力场 、静电力场
下页
3、几种常见的势能 ① 重力势能
0
Ep
M0
M
F保 dr
(取地面为零势能点)
0
E p (mg )dy mgy z mgy
y
WG Ep (mgy2 mgy1 )
② 万有引力势能 (选无穷远处为零势能点)
Ep
r
Mm Mm Mm G G 2 dr G r r r r
3–2-保守力与非保守力做功特点-势能知识分享
Ep
G
Mm (R h0 )G NhomakorabeaMm (R
h)
y h
GMm GMm
(R
1
h0 )
(R
1
h )
h h0 ( R h 0 )( R h )
h0 O
R
h , h 0 R
G
Mm R2
mg ( h h 0 )
首页
上页
下页
末页
退出
结论:
重力势能实际上近似等于质点在地面附近两点之 间的引力势能之差,只有当质点在地面附近时,我们 才可以用重力势能代替引力势能计算质点势能的变化 或质点相对于势能零点的势能值,当质点远离地球时, 就必须用质点的引力势能来研究质点的势能了。
物体移动的具体路径无关。
首页
上页
下页
末页
退出
3.万有引力做功
B
M对m的万有引力为
FGM r2 mer
m移动dr时,F 作元功为 M
rB dr rdr
θ
r
m F
d W F d r
rA
GM r2mer dr
A
B Mm
W F d rA Gr2erd r
首页
上页
下页
末页
退出
B Mm
W e r d r F d e r r d A r c Gr2 o ed rr d s r
保守力:力对质点做功而与质点移动的具体路径
无关,而只与质点的初末位置有关。
非保守力: 力所做的功与路
B
径有关。(例如摩擦力)
重力功 W(m2 gm y 1 g ) y D
L C
弹力功
W(1k 2
x2 21 2k1 x2)
最新《力学》漆安慎(第二版)答案04章
力学(第二版)漆安慎习题解答第四章动能和势能第四章 动能和势能 一、基本知识小结1、功的定义式:⎰⋅=2112r r rd F A直角坐标系中:⎰⎰+==221121,,1212y x y x yxx x x dy F dx F A dx F A ,自然坐标系中:⎰=2112s s ds F A τ极坐标系中: ⎰+=2211,,12θθθθr r rrd F dr F A2、⎰⋅-=-=b ap p k r d F a E b E mv E 保势能动能)()(,212重力势能m g y y E p =)(弹簧弹性势能 2)(21)(l r k r E p -=静电势能 rQqr E p πε4)(=3、动能定理适用于惯性系、质点、质点系 ∑∑∆=+k E A A 内外4、机械能定理适用于惯性系 ∑∑+∆=+)p k E E A A (非保内外5、机械能守恒定律适用于惯性系若只有保守内力做功,则系统的机械能保持不变,C E E p k =+6、碰撞的基本公式接近速度)(分离速度(牛顿碰撞公式)动量守恒方程)e v v e v v v m v m v m v m =-=-+=+)((2010122211202101对于完全弹性碰撞 e = 1 对于完全非弹性碰撞 e = 0对于斜碰,可在球心连线方向上应用牛顿碰撞公式。
7、克尼希定理 ∑+=22'2121i i c k v m mv E绝对动能=质心动能+相对动能应用于二体问题 222121u mv E c k μ+=212121m m m m m m m +=+=μ u 为二质点相对速率二、思考题解答4.1 起重机起重重物。
问在加速上升、匀速上升、减速上升以及加速下降、匀速下降、减速下降六种情况下合力之功的正负。
又:在加速上升和匀速上升了距离h 这两种情况中,起重机吊钩对重物的拉力所做的功是否一样多?答:在加速上升、匀速上升、减速上升以及加速下降、匀速下降、减速下降六种况下合力之功的正负分别为:正、0、负、正、0、负。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
内非保守力做负功的例子
内非保守力是指在物体运动过程中,由于摩擦、空气阻力等因素,物体所受的力不仅仅包括保守力,还包括非保守力。
而做负功则意味着力对物体的运动方向产生了反作用力,使物体失去了能量。
下面是一些内非保守力做负功的例子:
1. 摩擦力:当一个物体在表面上滑动时,摩擦力会产生反作用力,使得物体的运动速度减慢。
在这个过程中,摩擦力做负功,将物体失去了一部分能量。
2. 空气阻力:当物体在空气中运动时,空气阻力也会产生反作
用力,使得物体的速度减慢。
同样,空气阻力也会做负功,将物体失去能量。
3. 弹性力:当物体被压缩或拉伸时,弹性力会产生反作用力,
使物体恢复原来的形状。
在这个过程中,弹性力做负功,将物体失去了一部分能量。
以上是内非保守力做负功的一些例子,这些力会使物体失去能量,最终导致物体的速度降低或者停止运动。
- 1 -。
