五年级奥数平面图形的面积

合集下载

平面几何图形的周长和面积(五年级奥数9.28)

平面几何图形的周长和面积平面几何图形是小学数学的重要内容，在学习过程中，除了熟练地掌握各自的特征和周长、面积的意义，以及公式的推导过程，更重要的是要善于观察、勤于思考、手脑结合，学会并善于把有关知识加以整合、综合运用。

特别是针对一些较复杂的问题，通过变动图形的位置，或对图形进行适当的分割、拼补、旋转等手段，转化为规则图形的和差、倍比关系，化简为繁，使隐蔽的条件明朗化，从而找到最佳解题方法。

练习题1.一块长方形木板正好可以锯成12块边长2分米的正方形，这块木板的周长是多少？（损耗忽略不计）2.一块纱布长12米，宽1.9米，裁成两条直角边都是0.6米的三角巾，最多可以裁多少块？3.一个长方形的长和宽都增加了5cm2厘米，则面积比原来增加了145cm2，求原长方形的周长是多少？4.一个三角形的面积是平行四边形的3倍，三角形的底是平行四边形的一半，那么三角形的高是平行四边形的多少倍？5.任意四边形对角相边把四边形分成了甲乙丙丁四个三角形（如下图），已知甲的面积是15cm2，乙的面积是30cm2.丁的面积是18cm2，求三角形丙的面积。

6.大小两个正方形面积相差9cm2，边长相差1cm，求大正方形的周长和小正方形的面积。

7.如图大正方形中有一小正方形，它们的周长相差12cm2，面积相差39cm2,求它们的周长和。

8.如下图用同样的长方形瓷砖，在一个正方形小花坛周围围了一个正方形边框，边框的外围周长264cm，小花坛的面积为900cm2，问每块瓷砖的长和宽各是多少?9.从一个正方形惯皮卜射下一个寛为3分米的长方形一条以后，剩下的面彩是108平方分米，求原来正方形的面积。

10.一块黑板长0.6米，宽0.3米，写满了字，用一块长10厘米的长方形黑板擦，在黑板内紧沿黑板的边擦黑板一周(只做平移，不做旋转)，如果没有擦到的部分是黑板面积的一半，那么黑板擦的宽是多少?11.已知下图中，梯形的面积是11.2平方厘米，求阴影部分的面积。

五年级奥数培优《平面图形面积》(含答案)

平面图形的面积一（例题精讲）例1. 一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？例2. 正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

求中间长方形的面积。

例3.图中两个正方形的边长分别是6厘米和4厘米，求阴影部分的面积。

例4.如图所示，一大一小两个正方形中，已知阴影部分的面积是7平方厘米。

甲的面积是多少平方厘米？例5.下图中两个完全一样的三角形重叠在一起，求阴影部分的面积。

（单位：厘米）例6. 图中ABCD 是长方形，S 1比S 2的面积大6平方厘米，求EC 的长。

平面图形的面积一（课堂小测）7.求四边形ABCD 的面积。

（单位：厘米）8. 如下图长方形ABCD 的面积是16平方厘米，E 、F 都是所在边的中点，求三角形AEF 的面积。

9.右图中，正方形的边长4厘米，求长方形的面积。

10.如图，平行四边形BCEF 中，BC=8厘米，直角三角形中，AC=10厘米，阴影部分面积比甲的面积小8平方厘米。

平行四边形的高是多少厘米？A BCD 345°CD F CB DS 1A 4 6 S 2EE11.一个正方形的对角线长5厘米，这个正方形的面积是多少平方厘米？12.已知大正方形的边长是12厘米，求中间最小正方形的面积。

13.下图中，甲三角形的面积比乙三角形的面积大多少平方厘米？14.如图（单位：厘米）是两个相同的直角梯形重叠在一起，求阴影部分的面积。

15.如图所示，长方形的长12厘米，宽8厘米，A 、B 两点是长方形长和宽的中点，那么阴影部分的面积是多少？AB94 3 84 6乙甲5平面图形的面积二（例题精讲）例1. 一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？12×12＝144（平方厘米） 144÷4＝36（平方厘米）例2. 正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

五年级奥数——平面图形面积计算

年级授课日期授课主题第4讲——平面图形面积计算教学内容i.检测定位本讲所指平面图形面积计算主要指多边形及其组合图形面积的计算.这些图形面积计算一般都可以转化成三角形、长方形、平行四边形和梯形的面积计算，后者的计算公式都是我们在课内已经学过并且应该熟记的.主要的技巧在于如何将一般多边形及其组合图形“转化”为基本图形.【例1】在梯形中阴影部分面积是150平方厘米，求梯形面积.分析与解已知梯形上、下底长分别为15厘米和25厘米，令梯形高为h ，则由已知三角形面积为150平方厘米，有 h ⨯⨯=1521150，得).(20厘米=h 所以，梯形面积S 为.40020251521（平方厘米））（=⨯+⨯=S 随堂练习1如图2-4，已知平行四边形面积是48平方厘米，求阴影部分面积.【例2】如图3-4是两个完全相同的直角三角形叠在一起，求阴影部分的面积.（单位：分米）分析与解如图3-4，由于①+②的面积和②+③的面积相等，所以可以得出：①与③的面积相等，题目要求③的面积，其实只要求①的面积即可.所以（分米）；53-8==EF23)815(÷⨯+=S2313÷⨯=).(5.19239平方分米=÷=答：阴影部分的面积是19.5平方分米.【例3】如图4-4，将长为9厘米、宽为6厘米的长方形划分成四个三角形，其面积分别为1S 、2S 、3S 、4S ，且4321S S S S +==，求4S .分析与解设长方形面积为S ，则 )(54694321S S S S S +++==⨯=所以.184321=+==S S S S设x BE =，.y DF =则有 x S ⨯⨯==921181， .621182y S ⨯⨯== 解得 4=x ，.6=y 从而，2=EC ，.3=FC所以 332213=⨯⨯=S ， ).(153184平方厘米=-=S随堂练习2如图5-4，四边形ABCD 是直角梯形，其中ADE BC AB AD ∆===厘米，且厘米，厘米，15812、CDF DEBF ∆及四边形的面积相等，求三角形EBF 的面积.【例4】如图6-4，.904625︒=∠=∠====D B CD AB CF AE 厘米，厘米，厘米，厘米，求四边形AFCE 的面积.分析与解四边形AFCE 是不规则四边形，连结AC ，则AC 将四边形AFCE 分成两个三角形（AFC ∆、CEA ∆）.这两个三角形的面积利用已知条件可求.AB 是AFC ∆底边上的高，所以；平方厘米)(6622121=⨯⨯=⨯⨯=∆AB FC S AFC CD 是AE CEA 底边∆上的高，所以).(10452121平方厘米=⨯⨯=⨯⨯=∆CD AE S CEA 所以，四边形AFCE 的面积CEA AFC S S ∆∆+=).(16106平方厘米=+=随堂练习3如图7-4，四边形ABCD 中，，厘米，厘米，厘米，厘米，︒=∠=∠====901512105D B DC FC AB AE 求四边形AFCE 的面积.【例5】如图4-8，求长方形中阴影部分的面积.（单位：厘米）分析与解阴影部分的三个三角形高相等，那么它们的面积和就是它们的底的和乘高除以 2. .75215021015（平方厘米）=÷=÷⨯答：阴影部分的面积和是75平方厘米.【例6】如图9-4，平行四边形ABCD 的边长厘米10=BC ，直角三角形BCE 的直角边CE 长为8厘米.已知阴影部分的面积比三角形FEG 的面积大10平方厘米.求CF 的长.分析与解因为直角三角形BCE 与平行四边形ABCD 共有梯形BCFG .所以平行四边形ABCD 的面积比直角三角形BCE 的面积大10平方厘米.由已知可知CF 垂直AD ，所以，1021+⨯=⨯CE BC BC CF 即 .50108102110=+⨯⨯=⨯CF 所以.5（厘米）=CF随堂练习4如图10-4，正方形ABCD 的边长为12厘米，已知.2倍长度的是EC DE 求：（1）DEF ∆的面积；（2）CF 的长.玩一玩只剩一个如图，一个三角形的棋盘放着15个棋子，一开始随意取走一个棋子，出现一个空格.然后按以下规则开始跳棋子：棋子A 越过它的临格中的棋子B 跳到棋子B 另一侧相邻的空格中，并将B “吃”掉.按以上规则不断跳下去，每跳一步少一个棋.请问：能否跳到最后还剩一个棋子？请你玩一玩.图中的数是位子的编号，先不要看答案，自己动手画一张如图所示的棋盘，并在每个棋盘中放一枚棋子（可利用围棋子），然后按规则任意取走一个棋子，开始游戏.若有困难，可先看提示，继续游戏，最后再看方案.答案能.先取走1号、3号、5号位置上的棋子，依次从6号、10号、14号位置中的棋子起跳，经过13步可将棋盘中13个子“吃”掉.方案1 取走1号6→1,13→6,11→13,14→12,2→9,7→2,1→4,10→3,4→3,12→14,15→13，13→6,6→1（止于1号位）方案2 取走3号10→3,13→6,7→9,2→7,11→4,15→13,12→14,3→10,4→6,10→3,1→6,14→5,6→4（止于4号位）方案3 取走5号14→5,7→9，3→8，10→3，1→6 , 2→7 ，11→4,12→14,6→13,14→12,4→13,12→14,15→13（止于13号位） ii.针对培养1. 一块玉米地的形状如图所示，它的面积是_________平方米.2. 三个正方形如图所示放置，中心都重合，它们的边长依次是1厘米、3厘米、5厘米，那么图中阴影部分的面积是__________平方厘米.3. 如图，，，610==EC BC 直角三角形EDF 的面积比直角三角形FAB 的面积小5，那么长方形ABCD 的面积是__________4. 如图，正方形ABCD 的边长是9厘米，它的内部有一个内接三角形BFE ，厘米，厘米，24==DF AE 求三角形BFE 的面积.5. 如图，四边形ABCD 的两条对角线互相垂直相交于O ，厘米，厘米，54==BD AC 求四边形ABCD 的面积.6. 如图，四边形ABCD 中，厘米，厘米，，，3745,90==︒=∠︒=∠=∠AD BC BCD D B 求四边形ABCD 的面积.7. 如图由两个完全相同的梯形重叠在一起而组成，求图中阴影部分的面积.（单位：厘米）8. 如图，求阴影部分的面积.（单位：厘米）9. 如图，长方形的长为12厘米，宽为8厘米，图中阴影部分的面积与空白部分的面积哪个大？10. 如图，三角形ABC 的周长是30厘米，三角形内一点到三角形三条边的距离都是3厘米，求三角形ABC 的面积.11. 如图，已知正方形甲的边长为5厘米，正方形乙的边长为4厘米，那么图中阴影部分的面积是多少？12. 如图，ABCD 是长为8厘米、宽为6厘米的长方形，AF 长是4厘米，求阴影部分（三角形AEF ）的面积.13. 如图，长方形ABCD 与三角形EBC 重叠，已知三角形EFD 的面积比三角形ABF 的面积大6平方厘米，且厘米，厘米，64==BC CD 求ED 的长.。

五年级奥数组合图形面积

组合图形的面积1.基本平面图形特征及面积公式2.基本解题方法：由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先根据图形的基本关系，再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。

1.已知右面的两个正方形边长分别为6分米和4分米，求图中阴影部分的面积。

2.右图是两个相同的直角三角形叠在一起，求阴影部分的面积。

（单位：厘米）3.如图，这个长方形的长是9厘米，宽是8厘米，A和B是宽的中点，求长方形内阴影部分的面积。

4.在右图中，三角形EDF的面积比三角形ABE的面积大6平方厘米，已知长方形ABDC的长和宽分别为6厘米、4厘米，DF的长是多少厘米？5.正方形ABCD的面积是100平方厘米，AE=8厘米，CF=6厘米，求阴影部分的面积。

6.右图是一块长方形公园绿地，绿地长24米，宽16米，中间有一条宽为2米的道路，求草地（阴影部分）的面积。

7.如图，三角形ABC的面积是24平方厘米，且DC=2AD，E、F分别是AF、BC的中点，那么阴影部分的面积是多少？8.如下图，是一块长方形草地，长方形的长是16米，宽是10米，中间有两条宽2米的道路，一条是长方形，一条是平行四边形，那么有草部分（阴影部分）的面积有多大？9.如图，一个三角形的底长5米，如果底延长1米，那么面积就增加2平方米。

问原来的三角形的面积是多少平方米?1米组合图形的面积作业1.在右图中，三角形EDF的面积比三角形ABE的面积大75平方厘米，已知正方形ABCD的边长为15厘米，DF的长是多少厘米？2.如图，ABCD是一个长12厘米，宽5厘米的长方形，求阴影部分三角形ACE的面积。

3.已知正方形乙的边长是8厘米，正方形甲的面积是36平方厘米，那么图中阴影部分的面积是多少？4.如图，A、B两点是长方形长和宽的中点，那么阴影部分占长方形的面积是多少？5.如图，在平行四边形ABCD中，E、F分别是AC、BC的三等分点，且平行四边形的面积为54平方厘米，求S。

五年级奥数平面几何图形的面积计算

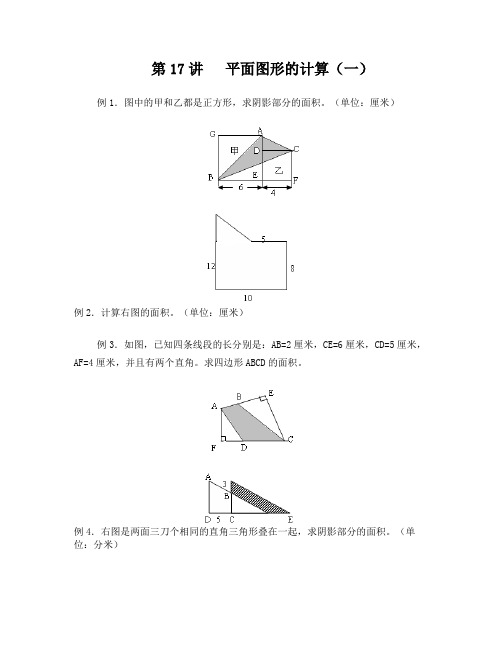
第17讲平面图形的计算（一）例1．图中的甲和乙都是正方形，求阴影部分的面积。

（单位：厘米）例2．计算右图的面积。

（单位：厘米）例3．如图，已知四条线段的长分别是：AB=2厘米，CE=6厘米，CD=5厘米，AF=4厘米，并且有两个直角。

求四边形ABCD的面积。

例4．右图是两面三刀个相同的直角三角形叠在一起，求阴影部分的面积。

（单位：分米）例5．下页左图是一块长方形草地，长方形的长是16，宽是10，中间有两条道路，一条是长方形，一条是平行四边形，那么，有草部分（阴影部分）的面积有多大？（单位：米）练习与思考1．求图中阴影部分的面积。

2．求图中阴影部分的面积。

3．下左图的长方形中，三角形ADE与四边形DEBF和三角形CDF的面积分别相等，求三角形DEF的面积。

4．四中平等四边形ABCD的边BC长10厘米，直角三角形BCE的直角边EC长8厘米，已知阴影部分的面积比三角形EFG的面积大10平方厘米，求CF的长。

5．图中三角形的高为4，面积为16；长方形的宽为6，长方形的面积是三角形面积的多少倍？6．如图，长方形的长是8，宽是6，A和B是宽的中点，求长方形内阴影部分的面积。

7．如图，BC长为5，求画斜线的两个三角形的面积之和。

8．上右图是两个一样的直角三角形重叠在一起，按照图上标出的数，计算阴影部分的面积。

9．右图是一块长方形草地，长方形长为16，宽为12，中间有一条宽为2的道路，求草地（阴影部分）的面积。

简便计算作业（12月23日）：1.996+19.97+199.82.894.68+4.686.11+4.68 754.7+15.925平均数问题作业（12月23日）：1.已知九个数的平均数是72.去掉一个数之后，余下的数的平均数是78。

去掉的数是多少？2.甲、乙、丙三个小组的同学去植树，甲、乙两组平均每组植树18棵，甲、丙两组平均每组植树17棵，乙、丙两组平均每组植树19棵。

三个小组各植树多少棵？3.五一班同学数学考试平均成绩91.5分，事后复查发现计算成绩时将一位同学的98分误作89分计算了。

小学五年奥数-平面图形的面积

平面图形的面积【试金石】例1如右图，已知一个四边形ABCD的两条边的长度AD=7，BC=3，三个角的度数：角B和角D是直角，角A是45°，求这个四边形的面积。

（单位；厘米）【针对性训练】如右图，已知一个四边形ABCD的两条边的长度AD=14厘米，BC=6厘米，三个角的度数：角B和角D是直角，角A是45°，求这个四边形的面积。

【试金石】例2右图中长方形的长是20厘米，宽是12厘米，求它的内部阴影部分的面积。

答：阴影部分的面积是120平方厘米。

【针对性训练】图中长方形的长是8米，宽是6米，A和B是宽的中点，求长方形内部阴影部分的面积。

【试金石】例3右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？（单位：分米）【针对性训练】右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？【试金石】例4如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米，求阴影部分的面积。

【针对性训练】如右图，甲、乙两图形都是正方形，它们的边长分别是6厘米和8厘米，求阴影部分的面积。

【试金石】例5【针对性训练】【试金石】【针对性训练】【智能提速训练营】1、如图，已知BD长是2厘米，DC长是3厘米，E是AD的中点，如果三角形ABD的面积是5平方厘米，那么三角形DEC的面积是多少？2、如图，已知平行四边形ABCD的面积是60平方分米，E、F分别是AB、AD边上的中点，图中阴影部分的面积是多少平方分米？3、如图，在平行四边形ABCD中，AE=ED，BF=FC，CG=GD，平行四边形ABCD的面积是阴影三角形EFG的多少倍？4、如图，BD=6厘米，BC=15厘米，△ABD的面积是24平方厘米，△ADC 的面积是多少平方厘米？5、右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？（单位：厘米）6、如图，梯形的面积是70平方厘米，上底8厘米，下底12厘米，阴影部分的面积是多少平方厘米？7、如图，四边形ABCD是平行四边形，DC=CE，如果△BCE的面积是15平方厘米，那么梯形ABED的面积是多少平方厘米？8、如图，平行四边形的面积是60平方厘米，阴影三角形的面积是多少平方厘米？9、如图，正方形ABCD的边长是4厘米，CG=3厘米，长方形DEFG的长DG=5厘米，那么它的宽DE是多少厘米？10、如图，四边形ABCD内有一点O，O点到四条边的垂线长都是4厘米，已知四边形的周长是36厘米，四边形ABCD的面积是多少平方厘米？11、如图，已知ABFE是平行四边形，ABCD是长方形，且AD=6厘米，AB=3厘米，CO=2厘米，阴影部分的面积是多少平方厘米？12、一个长方形被两条直线分成四个长方形，其中三个的面积分别是20平方米、25平方米和30平方米，阴影部分的面积是多少平方米？13、如右图，已知正方形ABCD和正方形CEFG，且正方形ABCD每边长为10厘米，求图中阴影（三角形BFD）部分的面积。

完整版)五年级奥数平面图形面积计算

完整版)五年级奥数平面图形面积计算五年级奥数第六讲——平面图形面积的计算一、知识要点1.基本平面图形特征及面积公式正方形：特征：四条边相等，四个角都是直角，有四条对称轴。

面积公式：S=边长的平方长方形：特征：对边相等，四个角都是直角，有二条对称轴。

面积公式：S=长×宽平行四边形：特征：两组对边平行且相等，对角相等，相邻的两个角之和为180°，容易变形。

面积公式：S=底边×高三角形：特征：两边之和大于第三条边，两边之差小于第三条边，三个角的内角和是180°，具有稳定性。

面积公式：S=底边×XXX÷2梯形：特征：只有一组对边平行，中位线等于上下底和的一半。

面积公式：S=(上底+下底)×高÷22.基本解题方法：由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先根据图形的基本关系，再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。

典型例题】例1】已知平行四边形的面积是28平方厘米，求阴影部分的面积。

例2】求图中阴影部分的面积。

例3】如图所示，甲三角形的面积比乙三角形的面积大6平方厘米，求CE的长度。

例4】两条对角线把梯形ABCD分割成四个三角形。

已知两个三角形的面积（如图所示），求另两个三角形的面积各是多少？练与拓展】1.计算下面图形的面积。

2.下面的梯形中，阴影部分面积是150平方厘米，求梯形的面积。

3.正方形ABCD的边长是12厘米，已知DE是EC长度的2倍，求三角形DEF的面积和CF的长。

4.平行四边形ABCD的边长BC=10厘米，直角三角形BCE的直角边EC长8厘米，已知阴影部分的面积比三角形EFG的面积大10平方厘米，求CF的长。

5.正方形ABCD的面积是100平方厘米，AE=8厘米，请计算以下图形的面积。

1.在一块长80米、宽30米的长方形地上，修了宽为2米和3米的两条小路，求草地的面积。

小学五年级奥数第13课《面积计算》试题附答案

小学五年级上册数学奥数知识点讲解第13课《面积计算》试题附答案第十四讲面积计算在小学阶段学习的各种平面图形之间有着密切的联系.我们把平面图形之间的转化方法及它们的面积、周长公式归纳如下图：计算图形的面积要用面积公式，对于一些复杂的图形有意识地运用运动变化的观点，将平面图形简单地变动位置，可以化繁为简，化难为易，从而获得最佳解法。

例1己知三角形ABC的面积为1, BE=2AB, BC=CD,求三角形BDE的面积? （下页图）例2求右图中阴影部分的面积.（大圆直径为2,单位：厘米）。

例3如下图在图中三角形ABE、ADF和四边形AECF的面积相等，求三角形AEF 的面积。

S，幺=&J&AEH — 3、§ △娅D - gQ^ABD同理，CGF =§S&BCD22因此3AAEH +Q&CGF = §(3&ABD + 二&BCD)=d、CLABCD2同理^ABFE +3&DHG =§、CJABCD，、4所以S&AEH +Q&CGF + ：&BFE += '^^□ABCD所以S[JEFGH = (1g) ScJABCD =□此CD即四边形EFGH的面积：四边形ABCD面积=5 ：9。

例8如右图，己知三角形ABC的三条高必定交于一点，如记成P点, 请你讲明黑+北+福=1为什么成立？AJJ b 匕Cr分析与解答从右图中可以看出APBC和AABC是同底的两个三角形, 它们的面积之比等于它们对应高的比，所以2=黑•.同理可得：L 右图是一个圆心角为45°的扇形，其中直角三角形B0C 的直角边为6厘米，求阴影部分面积。

2 .在右图中，阴影部分A 的面积比阴影部分B 的面积大10. 5平方厘米，求线段BC 的长度？sQ&PCA=PE $&PAB二西=PF CF'所以 s s s“△PBC 十 2&PCA 十 2 APABQ AAB CJ AAB C° AAB CPD PE PF = + + ——。

五年级奥数第4讲--平面图形的面积计算

2ห้องสมุดไป่ตู้
2
面积单位：平方千米，平方米，平方分米，平方厘米，平方毫米
※面积单位换算 1平方千米=100公顷 1公顷=10000平方米 1平方米=100平方分米 1平方分米=100平方厘米 1平方厘米=100平方毫米
常用解题策略
求解面积或可以归入此列的题型众多，一向是考试的重点和难点，牵涉的细节知识点也五花八门，十分考验应试者的综合几何学素养。熟练掌握常见图形的几何学性质，尤其是其面积公式，以及某些特殊图形的特殊之处（往往是出题关键）引以为面对此类问题的基本素养。灵活运用图形层面的加减技巧则称得上是制胜之道。山重水复之时逆向思维往往成为柳暗花明的点睛之笔。核心思想永远是将未知向已知转化，无论是尝试通过添加辅助线分割图形，还是利用等积变换和增补思想，亦或是在正面求解遇阻的情况下反向诉诸于从已知图形中“减” 出目标，无不围绕这一中心运转。
第 4讲平面图形的面积计算
我们已经学习过哪些平面图形：三角形、正方形、长方形、平行四边形、梯形以及圆、扇形等基本图形的面积计算，图形及计算公式如下：
正方形面积=边长×边长=a ，长方形面积=长×宽=ab，平行四边形面积=底×高=ah，圆面积=半径×半径×π=πr ，扇形面积=半径×半径×π×圆心角的度数÷360°
在实际问题中，我们遇到的往往不是基本图形，而是由基本图形组合、拼凑成的组合图形，它们的面积不能直接用公式计算。在本讲和后面的两讲中，我们将学习如何计算它们的面积。
谢谢

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

学生课程讲义
例题1
在梯形中阴影部分面积是150平方厘米，上底15厘米，下底25厘米，求梯形面积。

随堂练习1
如图，已知平行四边形面积是48平方厘米，求阴影部分面积。

梯形的上底
5厘米，高6
厘米。

例题2
如图，将长为9厘米，宽为6厘米的长方形，划分成四个三角形，其面积分别为S1、S2、S3、S4，且S1=S2=S3+S4，求S4。

随堂练习2
如图，四边形ABCD 是直角梯形，其中AD=12厘米，AB=8厘米，BC=15厘米，且△ADC 、四边形DEBF 及△CDF 的面积相等，求三角形EBF 的面积。

A E
D
例题3
如图，AE=5厘米，CF=2厘米，AB=6厘米，CD=4厘米，∠B=∠D=90度，求四边形AFCE 的面积。

随堂练习3
如图，四边形ABCD 中，AE=5厘米，AB=10厘米，FC=12厘米，DC=15厘米，∠B=∠D=90度，求四边形AFCE 的面积。

例题4
如图，在大正方形ABCD 里有一个内接长为6厘米，宽为1厘米的长方形，而且长方形的对称轴与正方形的对角线重合，求正方形的面积。

A E
B
F C
D
A
E
D
B F C
A
H D E
C B F G
随堂练习4 如图，正方形的面积为18.75平方厘米，在正方形内有两条平行于对角线的线段，将正方形平均分为面积相等的三份，
求平行线段AB 的长。

例题5
如图，平行四边形ABCD 的边长BC=10厘米，直角三角形BCE 的的直角边EC 长8厘米。

已知△BAG 和△FDC 面积的和比三角形FEG 的面积大10平方厘米，求CF 的长。

随堂练习5
如图，正方形ABCD 的边长是12厘米，已知DE 是EC 的长度的2倍。

求 1) △DEF 的面积 2) CF 的长。

例题6
B A A D B
C G F E
A B C F D
E
如图，长方形ABCD 与三角形EBC 重叠。

已知三角形EFD 的面积比ABF 的面积大6平方厘米，且CD=4厘米，BC=6厘米。

求ED 的长。

随堂练习6
如图，ABCD 是长方形，长是5厘米，宽4厘米。

AE 交CD 于F ，三角形甲的面积比三角形乙的面积大4平方厘米。

求CE 的长。

例题7
如图，长方型EFGH 的长和宽分别是6厘米和4厘米。

阴影的总面积为10平方厘米，求四边形ABCD 的面积。

随堂练习7 如图，三角形ABC 的面积是366平方厘米，是平行四边形CDEF 的面积的3倍。

求三角形BED 的面积。

E B A
F D
C A D
B E
甲乙 E F
H
G
A D E
例题8 如图，在△ABC 中，BD=2DC ，AE=3ED ，FC=7，求AF 。

随堂练习8
如图，由面积分别为2、3、5、7的四个三角形拼成一个大三角形ABC 。

问：图中三角形BEF 的面积是多少？
B F
C A B C
D
E A 2 C
F E B
D
3 5 7。