第四章三元合金相图
合集下载
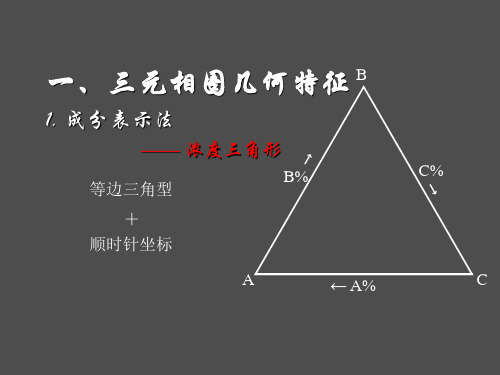
三元相图

三元相图1 浓度三角形(成分三角形):☐ 取一等边三角形,三个顶点表示三个纯组元。
☐ 三个边各定为100%,表示三个二元系A-B ,B-C ,C-A 的成分。
☐ 各边表示重量百分比。
2 双线法3 特殊直线 on 线:A 组元的含量相等。
Am 线:B,C 两组元含量之比为一常数。
4 等含量规则 -----MN 线上C 组元的含量相等定比例规则-------CD 线上A 、B 组元的含量之比是一定值。
5 等腰三角形法6 直角三角形法7 直线法则:三元系统两相平衡共存时,合金成分点与两平衡相的成分点必须位于同一条直线上。
MN 为共轭线杠杆定律:-----〉注意:共轭连线不可能位于从三角形顶点引出的直线上,根据选分结晶,液相中低熔点组元与高熔点组元的含量的比值应大于与之共存的固相中低,高熔点组元含量的比值。
8 重心法则:P211 处于三相平衡的合金,其成分点必位于共轭三角形的重心位置 9 三元匀晶相图:三个组元在液态和固态时都能够完全互溶10 P207 固溶体合金结晶过程中的蝴蝶形迹线:三元合金固溶体结晶过程中,反应两平衡对应关系的共轭连线并非是固定长度的水平线,随温度下降,它们一方面下移,另一方面绕成分轴转动。
11 变温截面图:---两种截取方法----从垂直截面图中可以得到准确的转变温度。
但不能确定两平衡相的成分及相对含量--- 与二元匀晶相图的差别:三元系变温截面截取三维相图中液相面及固相面所得的两条曲线并非是固相及液相的成分变化迹线,它们之间不存在相平衡关系,不能用杠杆定律确定相对含量。
12 P224 图5-108 两个垂直截面分析过程A BCM NA BC M N O ED F %100%100⨯=⨯=m n m o w m n on w αβ。
三元相图

L+ A+ B
L+A+C L+A+B+C
C C B+ B+ L+ L+
C B
A+B+C
A
L+B L+ A+ B
L+A+C L+ A C L+ L
C C B+ B+ L+ L+
e1
四、变温截面图
TA A3 A2 A1 TB E1 E3 TC E C3 C2 C1 E2 B3 B2 B1
A e
e3 e2
L
L+α
α
20
4. 垂直截面
类型一:
B
C
C
A
类型二:
B
C
A
• 从变温截面图可知: • (1)合金冷却过程中相变次序; • (2)转变温度范围; • (3)不同温度下相组成。
第三节 固态互不溶解的三元共晶相图 • 液态无限互溶,固态互不溶解,并且其中 任意两个组元具有共晶转变的三元相图。
一、相图空间模型
B
C
L L+A L+B L+A+C A+B+C L+B+A
A
B
C
34
e1
A e
TA A3 A2 A1 TB E1 TC E3 C3 C2 C1 E B3 B2 B1 E2
B
e2
e3
C
L L+A L+B L+A+C L+A+B L+B+C A+B+C
三元相图

• 1.立体图 • f=c-p+1 fmax=4 单相区
两相区
三相区 四相区
同析三角台
单相区(1个液相区,固溶体相、、的单相区)
液相面
相单相区为afmk与Aa之间的区域
a1aa0a0’a1为B 组元在相中的固溶度面 b1bb0b0’b1为A 组元在相中的固溶度面
两相区
三元共晶转变前 三元共晶转变后
4)三个固相平衡三棱台 A)三条棱为三条单变量线;也称同析线,即有一相同时析 出另两相,从而由单相区直接进入三相区; B) 顶面与四相平衡面重合,底面与成分三角形重合; C) 三个侧面是三相区和两相区(均为固相)的分界面; D)合金进入该相区后,随温度的下降,三相的相对量随之 发生改变(由重心定理可知)。 (
8.3 固态有限互 溶的三元共晶相 图
1. 空间模型
组元在固态有限互 溶的三元共晶相图的
空间模型,如图8.17 所示。
1)液相面和固相面
图中每个液、固两相平衡区和单相固溶体区之间都存 在一个和液相面共扼的固相面,即
固相面afmla和液相面ae1Ee3a共扼;
固相面bgnhb和液相面be1Ee2b共扼;
3)三元共晶转变面
成分为E的液相在水平面mnp(三元共晶转变面)发
生四相平衡的共晶转变:
Le1 ~ E f ~ m g ~ n Le2 ~ E h~ n i ~ p LE m n p Le3 ~ E k ~ p i ~ m
2.
投影图
图8.19 为三元共晶相图的 投影图。
从图中可清楚看到3条共晶转变线的投影e1E,e2E 和e3E把浓 度三角形划分成3个区域Ae1Ee3A , Be1Ee2B和C e2Ee3 C, 这是3个液相面的投影。 投影图中间的三角形mnp为四相平衡共晶平 面。
两相区
三相区 四相区
同析三角台
单相区(1个液相区,固溶体相、、的单相区)
液相面
相单相区为afmk与Aa之间的区域
a1aa0a0’a1为B 组元在相中的固溶度面 b1bb0b0’b1为A 组元在相中的固溶度面
两相区
三元共晶转变前 三元共晶转变后
4)三个固相平衡三棱台 A)三条棱为三条单变量线;也称同析线,即有一相同时析 出另两相,从而由单相区直接进入三相区; B) 顶面与四相平衡面重合,底面与成分三角形重合; C) 三个侧面是三相区和两相区(均为固相)的分界面; D)合金进入该相区后,随温度的下降,三相的相对量随之 发生改变(由重心定理可知)。 (
8.3 固态有限互 溶的三元共晶相 图
1. 空间模型
组元在固态有限互 溶的三元共晶相图的
空间模型,如图8.17 所示。
1)液相面和固相面
图中每个液、固两相平衡区和单相固溶体区之间都存 在一个和液相面共扼的固相面,即
固相面afmla和液相面ae1Ee3a共扼;
固相面bgnhb和液相面be1Ee2b共扼;
3)三元共晶转变面
成分为E的液相在水平面mnp(三元共晶转变面)发
生四相平衡的共晶转变:
Le1 ~ E f ~ m g ~ n Le2 ~ E h~ n i ~ p LE m n p Le3 ~ E k ~ p i ~ m
2.
投影图
图8.19 为三元共晶相图的 投影图。
从图中可清楚看到3条共晶转变线的投影e1E,e2E 和e3E把浓 度三角形划分成3个区域Ae1Ee3A , Be1Ee2B和C e2Ee3 C, 这是3个液相面的投影。 投影图中间的三角形mnp为四相平衡共晶平 面。
4相图三元相图

三
元
相 (3) 直角浓度三角形
图
1
2
3
5
6
7
8
9
2020/6/10
4 §4.9.1 三元相图的几何特性
第 4.9.1.2 直线法则与杠杆定理
九 节
直线法则:成分分别为α和β的三元合 金混合熔化后形成的新合金R,其成
三 分点必然在α和β的成分点连线上。
元 相
杠杆定理: W R
图 两条推论
W
R
(1)给定合金在一定温度下处 于两相平衡时,若其中一个相的成分 给定,另一个相的成分点必然位于已 知成分点连线的延长线上。
(9)
第 九
4.9.2.3 等温截面图
节
三 元 相 图
1
2
3
5
6
7
8
9
2020/6/10
4 §4.9.2 三元匀晶相图
(10)
第 九
4.9.2.4 垂直截面图
节
三 元 相 图
1
2
3
5
6
7
8
9
2020/6/10
4 §4.9.3 三元共晶相图
(11)
第 九 节
4.9.3.1 组元在液态完全互溶、固态完全不溶、具有共晶转变的 三元相图
三 元
(1)相图分析 • 点:熔点;二元共晶点;三元共晶点
相
两相共晶线
图
液相面交线
• 线:EnE 两相共晶面交线
液相单变量线
液相区与两相共晶面交线
液相面
两相区:3个
固相面
区: 单相区:4个
面: 两相共晶面
三相区:4个
三相共晶面
四相区:1个
三元相图

B% 50 40 30 20 10 A 90 80 70 80
90
10 20 30 40 50 C% 60 70 80 90
60
50 40 ← A%
30 20 10
C
课堂练习
90
B 10 20 30 40 50 C% 60 70 80 90 90 80 70 60 50 40 ← A% 30 20 10 C
第 四 章
第四章 三元相图-第九节三元相图 三元相图三、三元共晶相图
( 一) 组元在固态互不 相溶的共晶相图
组元在液态完全互溶、固 态完全不溶、具有共晶转变的 三元相图。
章 例题4.9.1
第 九 节 三 元 相 图 之 基 本 知 识
第 四 章
第四章 三元相图-第九节三 三元相图二、匀晶相图 元相图
匀晶转变:由液相直接结晶出单相固溶体的转变(相变) 匀晶转变
T (℃)
第 九 节 三 元 相 图 之 匀 晶 相 图
形成匀晶相图的条件 1.组元在液相、固相 均可完全互溶 2组元晶体结构相同、 原子尺寸、电负性相似 液相线 固相线 单相区 双相区
2)若两个平衡相的成分点已知,合金的成分点必然位 若两个平衡相的成分点已知, 于两个已知成分点的连线上。 于两个已知成分点的连线上。
第 四 章
第四章 三元相图-第九节三元相图 三元相图(4) 重心定律 在一定温度下,三元合金三相平衡时,合金的成分点为 在一定温度下,三元合金三相平衡时, 三个平衡相的成分点组成的三角形的质量重心。( 。(由相率可 三个平衡相的成分点组成的三角形的质量重心。(由相率可 此时系统有一个自由度,温度一定时, 知,此时系统有一个自由度,温度一定时,三个平衡相的成 分是确定的。) 分是确定的。)
90
10 20 30 40 50 C% 60 70 80 90
60
50 40 ← A%
30 20 10
C
课堂练习
90
B 10 20 30 40 50 C% 60 70 80 90 90 80 70 60 50 40 ← A% 30 20 10 C
第 四 章
第四章 三元相图-第九节三元相图 三元相图三、三元共晶相图
( 一) 组元在固态互不 相溶的共晶相图
组元在液态完全互溶、固 态完全不溶、具有共晶转变的 三元相图。
章 例题4.9.1
第 九 节 三 元 相 图 之 基 本 知 识
第 四 章
第四章 三元相图-第九节三 三元相图二、匀晶相图 元相图
匀晶转变:由液相直接结晶出单相固溶体的转变(相变) 匀晶转变
T (℃)
第 九 节 三 元 相 图 之 匀 晶 相 图
形成匀晶相图的条件 1.组元在液相、固相 均可完全互溶 2组元晶体结构相同、 原子尺寸、电负性相似 液相线 固相线 单相区 双相区
2)若两个平衡相的成分点已知,合金的成分点必然位 若两个平衡相的成分点已知, 于两个已知成分点的连线上。 于两个已知成分点的连线上。
第 四 章
第四章 三元相图-第九节三元相图 三元相图(4) 重心定律 在一定温度下,三元合金三相平衡时,合金的成分点为 在一定温度下,三元合金三相平衡时, 三个平衡相的成分点组成的三角形的质量重心。( 。(由相率可 三个平衡相的成分点组成的三角形的质量重心。(由相率可 此时系统有一个自由度,温度一定时, 知,此时系统有一个自由度,温度一定时,三个平衡相的成 分是确定的。) 分是确定的。)
物理化学三元相图
始晶相
A3
A2 A1
TA E A3 A2 A1
E1
B2
B1
LA+ B
——
TB E1 B3 B2 E2 B1
A
A1 E3 E
E3
TC E C3 C2 C1
B
E2
B3
B1 E
C3 C1
C
C2 C1
L B +C
LA+ C
LA+ C
LA+ B
A
L A+B
e
B
C
L B +C
LA+ B + C
50
C%
60 70 80 90 IV 50 40 ← A% 30 20 10 C
课堂练习
90 2. 标出 75%A+10%B+15%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B 10 20 30 40
50
C%
60 70 80 90 50 40 ← A% 30 20 10 C
两相区 三相区 四相区 同析三角台
单相区 (1个液相区,固溶体相、、的单相区)
3个液相面以上 的区域——1个 液相区
单相区 (1个液相区,固溶体相、、的单相区)
课堂练习
90 3. 标出 50%A+20%B+30%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B 10 20 30 40
50
C%
60 70 80 90 50 40 ← A% 30 20 10 C
B 2. 浓度三角形中具有特定意义的直线 90 II点:20%A- 50%B- 30%C III 点:20%A- 20%B- 60%C IV 点:40%A- 0%B- 60%C 80 70 II 10 20 30
A3
A2 A1
TA E A3 A2 A1
E1
B2
B1
LA+ B
——
TB E1 B3 B2 E2 B1
A
A1 E3 E
E3
TC E C3 C2 C1
B
E2
B3
B1 E
C3 C1
C
C2 C1
L B +C
LA+ C
LA+ C
LA+ B
A
L A+B
e
B
C
L B +C
LA+ B + C
50
C%
60 70 80 90 IV 50 40 ← A% 30 20 10 C
课堂练习
90 2. 标出 75%A+10%B+15%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B 10 20 30 40
50
C%
60 70 80 90 50 40 ← A% 30 20 10 C
两相区 三相区 四相区 同析三角台
单相区 (1个液相区,固溶体相、、的单相区)
3个液相面以上 的区域——1个 液相区
单相区 (1个液相区,固溶体相、、的单相区)
课堂练习
90 3. 标出 50%A+20%B+30%C 80 的合金 70 60 B% 50 40 30 20 10 A 90 80 70 60
B 10 20 30 40
50
C%
60 70 80 90 50 40 ← A% 30 20 10 C
B 2. 浓度三角形中具有特定意义的直线 90 II点:20%A- 50%B- 30%C III 点:20%A- 20%B- 60%C IV 点:40%A- 0%B- 60%C 80 70 II 10 20 30
三元合金相图

第五章
• 三维空间立体图 • 多元可作伪三元处理
内容
5.1
5.2 5.3 5.4 5.5 5.6
表示方法
相平衡定量法则 三元匀晶相图 三元共晶相图 三元相图总结 三元相图举例
5.1 表示方法
一、浓度三角形
三元合金有三个组元A、B、C,需满足一个约束条件: XA+XB+XC=100% 两个组元独立可变,需用一个平面表示 ——浓度三角形。 (1)直角三角形 B xB A C A
相 图 发 展 而 来 。
e1
β e3
TC E B
e2
α
γ
A C
TA> TB >TC >e1>e2>e3>TE
相 区:
• 单相区:L、α、β、γ f=3 任意形状空间区域。 与三个两相区衔接。
α
L+α
A
α+β α+γ
双相区: L+α L+β L+γ e1 e2 α
E
L→α L→β L→γ
TA
一对成分共轭面包围的空间区域, 两平衡相的浓度在共轭面上 按蝴蝶规律变化。 f=2
Fe-13%Cr-0.2%C 合金: — 2Cr13成分点 O,在1150℃位 于γ区,为单相奥 氏体。
Fe-13%Cr-2%C 合金:
C
C1
1150℃
C2 b C3
L + γ+ C1
C
γ a
Fe
o
α
Cr
3、Fe-C-Si系垂直截 面图
• 1-2 L→γ
• 2-3 L→γ+C
L +δ
L +δ+γ
• 三维空间立体图 • 多元可作伪三元处理
内容
5.1
5.2 5.3 5.4 5.5 5.6
表示方法
相平衡定量法则 三元匀晶相图 三元共晶相图 三元相图总结 三元相图举例
5.1 表示方法
一、浓度三角形
三元合金有三个组元A、B、C,需满足一个约束条件: XA+XB+XC=100% 两个组元独立可变,需用一个平面表示 ——浓度三角形。 (1)直角三角形 B xB A C A
相 图 发 展 而 来 。
e1
β e3
TC E B
e2
α
γ
A C
TA> TB >TC >e1>e2>e3>TE
相 区:
• 单相区:L、α、β、γ f=3 任意形状空间区域。 与三个两相区衔接。
α
L+α
A
α+β α+γ
双相区: L+α L+β L+γ e1 e2 α
E
L→α L→β L→γ
TA
一对成分共轭面包围的空间区域, 两平衡相的浓度在共轭面上 按蝴蝶规律变化。 f=2
Fe-13%Cr-0.2%C 合金: — 2Cr13成分点 O,在1150℃位 于γ区,为单相奥 氏体。
Fe-13%Cr-2%C 合金:
C
C1
1150℃
C2 b C3
L + γ+ C1
C
γ a
Fe
o
α
Cr
3、Fe-C-Si系垂直截 面图
• 1-2 L→γ
• 2-3 L→γ+C
L +δ
L +δ+γ
三元合金相图和凝固

2.固态有限溶解三元共晶合金的凝固过程和组织
合金IV L→α,L→α+γ,α→γ, 合金VI:L→α,L→α + γ,
L→β+α+γ α → β 同析反应
→ γ →
固态有限溶解三元共晶合金的凝固过程和 组织
2 4
3
3.
固态有限溶解三元共晶合金的等温截面
4.
固态有限溶解三元共晶合金的变温截面
三元相图
一、三元相图的成分表示法 二、杠杆定律及重心法则 三、匀晶三元相图 四、简单三元共晶相图 五、固态有限溶解的三元共晶相图 六、有包共晶反应的三元相图 七、 三元包晶相图 八、形成稳定化合物的三元相图 九、三元相图分析法总结 十、三元相图实例
必要性:工业材料为多元合金 本章主要内容: 1. 三元相图的表达方式,使用方法 2.几种基本的三元相图立体模型 3.各种等温截面,变温截面及各相区在浓 度三角形上的投影图 4.典型合金的凝固过程及组织,各种相变过程及 相平衡关系。
一、三元相图的成分表示法
1.浓度等边三角形:
三个顶点为纯组元,三条边为二元合金,三角形内任一点为三 元合金
一.三元相图的成分表示法:等腰三角形
一.三元相图的成分表示法:直角坐标系
三、匀晶Байду номын сангаас元相图
1. 立体模型 液相区,固相区,液、固两相区
匀晶三元相图---合金凝固过程及组织 a.平衡凝固 b.蝶形法则:如图
L→A+B+C, 练习:分析p-f之间合金的结晶过程
五、固态有限溶解的三元共晶相图
1. 固态有限溶解三元共晶立体模型 三个液相面,三个固溶体相面,一个三元共晶固相面 三个二元共晶完毕固相面, 三组二元共晶开始面
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
TC E3 E B3 B2 B1
e3
C
L L+A
A
E2
B
C3 C2
C1
L+B
L+A+B A+B+C
47
L+A+C
L+B+C
C
e1
A e
TA A3 A2 A1 TB E1 TC E3 C3 C2 C1 E L+A B3 B2
B
e2
e3
B1
E2
C
L
A
B
L+B
L+A+C
L+B+C
A+B+C
48
C
49
e1
6
二、在成分三角形中具有特定意义的直线
(一)平行于三角形某一条边的直线
凡成分位于该线上的合金,其所含的、由这条
边对应顶点所代表的组元的含量为一定值。
平行于AC的直线上的
P 与 Q 合金所含 B 组元的
数量相等( b%B ),但 是,它们所含A与C组元 的数量不同。
含B组元相等的直线
7
(二)通过三角形顶点的任一直线
f=2
在等温截面上,平衡相的成分由两相区的连接线
确定,可以应用杠杆定律计算相的含量。
在变温截面上,只能判断两相转变的温度范围,
不能确定各个平衡相的成分,不能用杠杆定律计算
相的含量。
70
二、三元系的三相平衡 f=1 三相区的立体模型是一个三棱柱体。 三相区的等温截面是一个直边三角形,三个顶点 即三个相的成分点,可以用重心法则计算各相的含
个纯组元。
A-B、B-C、C-A简单二元合金的浓度坐标。凡是 位于三角形边上的合金,都是二元合金。
位于等边三角形内任意一点的合金,都是三元
合金。
3
实际三元相图的成分三角形有时会标上网格。一
般均沿顺时针(有时也沿逆时针)一个方向标注组
元的浓度。
有网格的成分三角形
4
其它的成分三角形
(1)等腰成分三角形
21
三、等温截面(水平截面)
B
C
A
22
三元匀晶相图的等温截面
合金O在t1温度下固相和液相L的含量分别为: w= nO/mn100% wL= mO/mn100% 23
四、变温截面(垂直截面)
类型一:
L L+
B D
C
D
C
A
24
类型二:
L
L+
B
E
C F
E
ห้องสมุดไป่ตู้
F A
25
26
变温截面与二元匀晶相图的区别
L+B
C
A+B+C
51
52
二、组元在固态有限溶解,具有共晶转变的相图
(一)相图分析
固态下有限溶解的 三元共晶相图
53
固态下有限溶解的三元共晶相图
54
1. 液相面
55
2. 固相面 1 )三个固溶体( 、 、)相区的固相面
56
2)一个三元共晶面
57
3 ) 三 个二 元 共 晶 转 变 结束面
液相面投影图
固相面投影图
匀晶相图投影图
28
第四节 三元共晶相图
一、组元在固态完全不溶的共晶相图
(一)相图分析
三组元在液态能 无 限 互 溶 , 在 固 态几 乎 完 全 互 不 溶 解 ,并
且 其 中 任 两 个 组 元具
有 共 晶 转 变 , 形 成简 单的三元共晶相图。
29
组元在固态完全不互溶的三元共晶相图30
若两个平衡相的成分点已知,合金的成分点必然
位于两个已知成分点的连线上。
12
二、重心法则
成分为R点的合 金分解为 、 、 三相。
当一个三元合金R分解为 三个不同成分的平衡相 、 和时,合金成分点R必定 位于△ 的重心(三相的 质量重心,不是三角形的
几何重心)位置上。 、 和 三个相的质量分数可以
三元相图的重心法则
% = Rd/d100% % = d/(1-%) = d/R/d100% % = d/(1-%) = d/R/d100%
14
第三节 三元匀晶相图
一、相图分析
三个组元在液态 及固态均无限溶解
的相图称为三元匀
晶相图。
15
B
C
A
TA A3 A2 A1 TB E1 E3 TC E2 B3 B2
B e
e3 e2
B1
A
B
E
L L+A L+A+C
C
C3 C2 C1
L+B L+A+B A+B+C
50
C
e1
A
TA
A3 A2 A1 TB E1 TC E3 C3 C2 E2 B3 B2 B1
B e
e3 e2
C
L L+A
A
B
E
C1
L+A+C
为 和 ,根据直线法则, 、 P、 三点必在同一直线上。 然后应用杠杆定律计算平衡 两相的相对量。
% = P/100%
% = P/100%
11
规律:
当给定合金在一定温度下处于两相平衡状态时, 若其中一相的成分给定,则根据直线法则,另一相 的成分点必定位于两个已知成分点的延长线上。
End
80
当三元系中某一组元含量 较少,而另两个组元含量较 多时,合金成分点将靠近等 边三角形的某一边。可将成 分三角形两腰放大,成为等 腰三角形。左图中,由于成 分点 O 靠近底边,所以在实 际应用中只取等腰梯形部分 即可。
5
等腰成分三角形
(2)直角成分三角形
当三元系成分以某一组 元为主、其它两个组元成 分很少时,合金成分点将 靠近等边三角形某一顶角 。若采用直角坐标表示成 分,则可使该部分相图清 楚地表示出来。 例如,左图中的 P 点是 成 分 为 wMn=0.8% , wSi=0.6% , 余 量 为 Fe 的 合金。
第四章
三元合金相图
第一节
三元合金相图的表示方法
一、成分三角形( 浓度三角形)
在三元相图中,通常采
用等边三角形表示成分, 这种三角形通常称为成分
三角形(或浓度三角形)。
图中 O合金所含 A、 B、
C 三个组元的浓度分别为
a%A、b%B、c%C。
2
等边三角形的三个顶点,分别表示 A、B、C三 等边三角形的三条边AB、BC、CA,分别表示
三元共晶点:E 四相平衡转变:
(三元共晶转变) 四相区:△A1B1C1
34
相 区
35
单相区:一个 L 双相区:三个 L + A、L + B、L + C
三相区:四个
L + A + B、L + B +C、 L + A + C、A + B + C 四相区:一个 L+A+B+C
36
(二)投影图及合金的结晶过程
凡成分位于该直线上的三元合金,其所含的、由
另两个顶点所代表的两组元的量之比是恒定的。 BD 线上的合金 E 与 F , 分别含A、C两个组元
的浓度比值保持不变,
即 (A%/C%)E= Ba1/Bc1 =Ba2/Bc2=(A%/C%)F =(A%/C%)D=CD/AD
A%/C%=常数的直线
=常数
8
58
59
3. 二元共晶区
60
61
同析三角台
三相区
62
4. 溶解度曲面
单析面投影图
63
同析面投影图
64
5. 单变量线
65
6. 相 区
66
(二)投影图
各类合金的 平衡结晶过程 及其组织组成 物与相组成物 见表5-2。
67
(三)等温截面
68
(四)变温截面
69
第五节 三元相图总结
一、三元系的两相平衡
三个液相面:
tAE1EE3tA:L A
tBE1EE2tB: L B
tCE2EE3tC: L C 二元共晶线: E1E、E2E、E3E
31
三相平衡区和两相共晶面
32
三元共晶相图的三相区是以三条单变量线作为棱边的 空间三棱柱体。在水平截面上三相区一定是直边三角形, 三个顶点是三个平衡相的成分。每个三角形内是该温度下 的三相平衡区。 33
两者成分坐标的含义不同。 变温截面两相区的形状与二元匀晶相图的不同。 当变温截面中的纵坐标不是纯组元时,液相线与固 相线不闭合。 变温截面中的液相线和固相线不代表相图中合金 的液相和固相的平衡成分随温度变化的轨迹,不能
根据液相线和固相线应用直线法则和杠杆定律计算
相的含量。
27
五、投影图
若四相均为固相,则四相平衡反应可能有以下三类:
74
四相平衡类型的判断
(1)根据四相平面的形状及与其相连的三相区的位
置来判断。
75
76
(2)根据三条液相单变量线的走向判断。
(3)从截过四个三相区的变温截面上判断。
77
(4)根据单变量线的位置和走向判断。
三元共晶反应 包共晶反应 三元包晶反应
A E1
B
E E3
E2
C
三元共晶相图的投影图
37
38
39
40
41
(三)等温截面
42
43
44
L+C L
e3
C
L L+A
A
E2
B
C3 C2
C1
L+B
L+A+B A+B+C
47
L+A+C
L+B+C
C
e1
A e
TA A3 A2 A1 TB E1 TC E3 C3 C2 C1 E L+A B3 B2
B
e2
e3
B1
E2
C
L
A
B
L+B
L+A+C
L+B+C
A+B+C
48
C
49
e1
6
二、在成分三角形中具有特定意义的直线
(一)平行于三角形某一条边的直线
凡成分位于该线上的合金,其所含的、由这条
边对应顶点所代表的组元的含量为一定值。
平行于AC的直线上的
P 与 Q 合金所含 B 组元的
数量相等( b%B ),但 是,它们所含A与C组元 的数量不同。
含B组元相等的直线
7
(二)通过三角形顶点的任一直线
f=2
在等温截面上,平衡相的成分由两相区的连接线
确定,可以应用杠杆定律计算相的含量。
在变温截面上,只能判断两相转变的温度范围,
不能确定各个平衡相的成分,不能用杠杆定律计算
相的含量。
70
二、三元系的三相平衡 f=1 三相区的立体模型是一个三棱柱体。 三相区的等温截面是一个直边三角形,三个顶点 即三个相的成分点,可以用重心法则计算各相的含
个纯组元。
A-B、B-C、C-A简单二元合金的浓度坐标。凡是 位于三角形边上的合金,都是二元合金。
位于等边三角形内任意一点的合金,都是三元
合金。
3
实际三元相图的成分三角形有时会标上网格。一
般均沿顺时针(有时也沿逆时针)一个方向标注组
元的浓度。
有网格的成分三角形
4
其它的成分三角形
(1)等腰成分三角形
21
三、等温截面(水平截面)
B
C
A
22
三元匀晶相图的等温截面
合金O在t1温度下固相和液相L的含量分别为: w= nO/mn100% wL= mO/mn100% 23
四、变温截面(垂直截面)
类型一:
L L+
B D
C
D
C
A
24
类型二:
L
L+
B
E
C F
E
ห้องสมุดไป่ตู้
F A
25
26
变温截面与二元匀晶相图的区别
L+B
C
A+B+C
51
52
二、组元在固态有限溶解,具有共晶转变的相图
(一)相图分析
固态下有限溶解的 三元共晶相图
53
固态下有限溶解的三元共晶相图
54
1. 液相面
55
2. 固相面 1 )三个固溶体( 、 、)相区的固相面
56
2)一个三元共晶面
57
3 ) 三 个二 元 共 晶 转 变 结束面
液相面投影图
固相面投影图
匀晶相图投影图
28
第四节 三元共晶相图
一、组元在固态完全不溶的共晶相图
(一)相图分析
三组元在液态能 无 限 互 溶 , 在 固 态几 乎 完 全 互 不 溶 解 ,并
且 其 中 任 两 个 组 元具
有 共 晶 转 变 , 形 成简 单的三元共晶相图。
29
组元在固态完全不互溶的三元共晶相图30
若两个平衡相的成分点已知,合金的成分点必然
位于两个已知成分点的连线上。
12
二、重心法则
成分为R点的合 金分解为 、 、 三相。
当一个三元合金R分解为 三个不同成分的平衡相 、 和时,合金成分点R必定 位于△ 的重心(三相的 质量重心,不是三角形的
几何重心)位置上。 、 和 三个相的质量分数可以
三元相图的重心法则
% = Rd/d100% % = d/(1-%) = d/R/d100% % = d/(1-%) = d/R/d100%
14
第三节 三元匀晶相图
一、相图分析
三个组元在液态 及固态均无限溶解
的相图称为三元匀
晶相图。
15
B
C
A
TA A3 A2 A1 TB E1 E3 TC E2 B3 B2
B e
e3 e2
B1
A
B
E
L L+A L+A+C
C
C3 C2 C1
L+B L+A+B A+B+C
50
C
e1
A
TA
A3 A2 A1 TB E1 TC E3 C3 C2 E2 B3 B2 B1
B e
e3 e2
C
L L+A
A
B
E
C1
L+A+C
为 和 ,根据直线法则, 、 P、 三点必在同一直线上。 然后应用杠杆定律计算平衡 两相的相对量。
% = P/100%
% = P/100%
11
规律:
当给定合金在一定温度下处于两相平衡状态时, 若其中一相的成分给定,则根据直线法则,另一相 的成分点必定位于两个已知成分点的延长线上。
End
80
当三元系中某一组元含量 较少,而另两个组元含量较 多时,合金成分点将靠近等 边三角形的某一边。可将成 分三角形两腰放大,成为等 腰三角形。左图中,由于成 分点 O 靠近底边,所以在实 际应用中只取等腰梯形部分 即可。
5
等腰成分三角形
(2)直角成分三角形
当三元系成分以某一组 元为主、其它两个组元成 分很少时,合金成分点将 靠近等边三角形某一顶角 。若采用直角坐标表示成 分,则可使该部分相图清 楚地表示出来。 例如,左图中的 P 点是 成 分 为 wMn=0.8% , wSi=0.6% , 余 量 为 Fe 的 合金。
第四章
三元合金相图
第一节
三元合金相图的表示方法
一、成分三角形( 浓度三角形)
在三元相图中,通常采
用等边三角形表示成分, 这种三角形通常称为成分
三角形(或浓度三角形)。
图中 O合金所含 A、 B、
C 三个组元的浓度分别为
a%A、b%B、c%C。
2
等边三角形的三个顶点,分别表示 A、B、C三 等边三角形的三条边AB、BC、CA,分别表示
三元共晶点:E 四相平衡转变:
(三元共晶转变) 四相区:△A1B1C1
34
相 区
35
单相区:一个 L 双相区:三个 L + A、L + B、L + C
三相区:四个
L + A + B、L + B +C、 L + A + C、A + B + C 四相区:一个 L+A+B+C
36
(二)投影图及合金的结晶过程
凡成分位于该直线上的三元合金,其所含的、由
另两个顶点所代表的两组元的量之比是恒定的。 BD 线上的合金 E 与 F , 分别含A、C两个组元
的浓度比值保持不变,
即 (A%/C%)E= Ba1/Bc1 =Ba2/Bc2=(A%/C%)F =(A%/C%)D=CD/AD
A%/C%=常数的直线
=常数
8
58
59
3. 二元共晶区
60
61
同析三角台
三相区
62
4. 溶解度曲面
单析面投影图
63
同析面投影图
64
5. 单变量线
65
6. 相 区
66
(二)投影图
各类合金的 平衡结晶过程 及其组织组成 物与相组成物 见表5-2。
67
(三)等温截面
68
(四)变温截面
69
第五节 三元相图总结
一、三元系的两相平衡
三个液相面:
tAE1EE3tA:L A
tBE1EE2tB: L B
tCE2EE3tC: L C 二元共晶线: E1E、E2E、E3E
31
三相平衡区和两相共晶面
32
三元共晶相图的三相区是以三条单变量线作为棱边的 空间三棱柱体。在水平截面上三相区一定是直边三角形, 三个顶点是三个平衡相的成分。每个三角形内是该温度下 的三相平衡区。 33
两者成分坐标的含义不同。 变温截面两相区的形状与二元匀晶相图的不同。 当变温截面中的纵坐标不是纯组元时,液相线与固 相线不闭合。 变温截面中的液相线和固相线不代表相图中合金 的液相和固相的平衡成分随温度变化的轨迹,不能
根据液相线和固相线应用直线法则和杠杆定律计算
相的含量。
27
五、投影图
若四相均为固相,则四相平衡反应可能有以下三类:
74
四相平衡类型的判断
(1)根据四相平面的形状及与其相连的三相区的位
置来判断。
75
76
(2)根据三条液相单变量线的走向判断。
(3)从截过四个三相区的变温截面上判断。
77
(4)根据单变量线的位置和走向判断。
三元共晶反应 包共晶反应 三元包晶反应
A E1
B
E E3
E2
C
三元共晶相图的投影图
37
38
39
40
41
(三)等温截面
42
43
44
L+C L
