运筹学课程设计-一个飞行管理问题
第8组 飞行管理问题分析

飞行管理问题分析摘要本文讨论了飞行管理问题,根据在该区域内飞机的初始位置、初始速度与角度,首先推导出了任意时刻位置的坐标,然后计算出任意两架飞机的距离,根据给定的初始条件推导出了互不相撞条件,即飞行约束条件。
然后在根据这一约束条件我们建立了一个非线性动态规划模型,但是由于模型求解过于繁琐,约束条件过于复杂,所以在问题的分析过程中对约束条件进行了放宽,设计了一个matlab算法,利用计算机求解,根据题目给定的要求,我们把各个飞机飞行角度变化的平方之和作为目标函数,最终的到如下得结果:本文的解法简单,容易理解,因为对约束条件进行了放宽所以本文得到的最终结果与理论相比较会有所偏大。
关键词:飞行管理、飞行角度、相距距离、角度变化,非线性规划。
一、问题的重述1问题的背景.随着科技的不管进步,飞机已经成为了一种必不可少的交通工具,同时人们也日益关注飞行安全。
对飞行线路的研究以及对于突发情况的应对措施关系着大家的生命安全。
2.问题的提出在约10000m高空的某边长160km的正方形区域内,经常有若干架飞机作水平飞行,区域内每架飞机的位置和速度向量均由计算机记录其数据,以便进行飞行管理.当一架欲进入该区域的飞机到达边界区域边缘时, 记录其数据后,要立即计算并判断是否会与其区域内的飞机发生碰撞.如果会碰撞,则应计算如何调整各架(包括新进入的)飞机飞行的方向角,以避免碰撞.现假设条件如下:1) 不碰撞的标准为任意两架飞机的距离大于8km;2)飞机飞行方向角调整的幅度不应超过30度;3)所有飞机飞行速度均为每小时为800km;4)进入该区域的飞机在到达区域边缘时,与区域内飞机的距离应在60km以上;5)最多考虑6架飞机;6)不必考虑飞机离开此区域后的状况;二、基本假设1.题目给定的数据真实可靠,具有代表性。
2.不考虑飞机转变航向时所需要的时间及转弯半径。
3.不考虑飞机体积大小。
4.飞机飞行稳定,不受其他因素影响,比如气流,天气。
运筹学课程设计案例(航班问题)
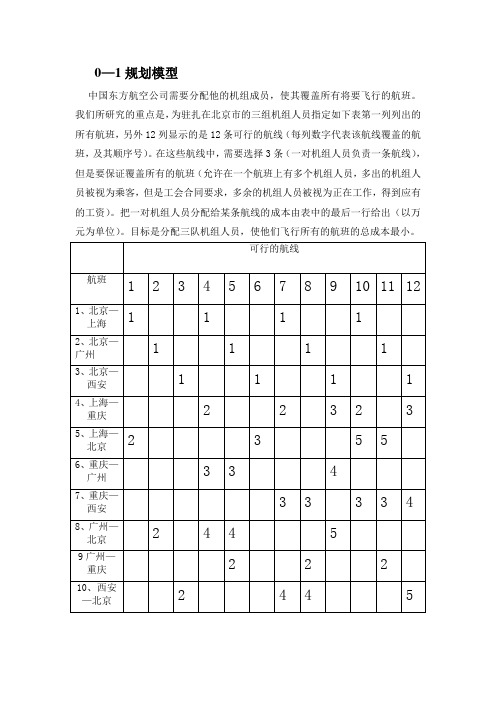
0—1规划模型中国东方航空公司需要分配他的机组成员,使其覆盖所有将要飞行的航班。
我们所研究的重点是,为驻扎在北京市的三组机组人员指定如下表第一列列出的所有航班,另外12列显示的是12条可行的航线(每列数字代表该航线覆盖的航班,及其顺序号)。
在这些航线中,需要选择3条(一对机组人员负责一条航线),但是要保证覆盖所有的航班(允许在一个航班上有多个机组人员,多出的机组人员被视为乘客,但是工会合同要求,多余的机组人员被视为正在工作,得到应有的工资)。
把一对机组人员分配给某条航线的成本由表中的最后一行给出(以万元为单位)。
目标是分配三队机组人员,使他们飞行所有的航班的总成本最小。
用0—1变量建模有12条可行的航线,相应的,我们有12个是或否的决策:应该指定一地机组人员飞行j航线吗?(j=1,2, (12)因此,我们使用12个0-1变量分别代表这些决策:1,如果给航线j指定一组机组人员;X j=0,否则。
该模型最有趣的地方是,每个约束条件实际上是保证一个航班被覆盖。
例如考虑表中的最后一个航班(西安到上海)。
五条航线(也就是6航线、9航线、10航线、11航线和12航线)包括航班,因此,公司之上会选择其中一条航线飞行。
结果约束条件是x6+x9+x10+x11+x12≥1对另外11个航班使用类似的约束完成BIP模型是Min=2X1+3X2+4X3+6X4+7X5+5X6+7X7 +8X8+9X9+9X10+8X11+9X12s.t.x1+x4+x7+x10≥1 (北京—上海)x2+x5+x8+x11≥1 (北京—广州)x3+x6+x9+x12≥1 (北京—西安)x4+x7+x9+x10+x12≥1 (上海—重庆)x1+x6+x10+x11≥1(上海—北京)x4+x5+x9≥1(重庆—广州)x7+x8+x10+x11+x12≥1(重庆—西安)x2+x4+x5+x9≥1(广州—北京)x5+x8+x11≥1(广州—重庆)x3+x7+x8+x12≥1(西安—北京)x6+x9+x10+x11+x12≥1 (西安—上海)x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+ x12=3 (共三队机组成员)且x j是0-1变量。
一个飞行管理问题数模竞赛

一个飞行管理问题摘要在某一空域里对飞机的飞行合理管理事关重大�比如乘客及机上工作人员生命财产安全和航空公司的运作效益等。
本文通过对飞机飞行管理问题的研究�得到了调整飞机架数较少同时调整幅度均最小�平方和最小�的飞行管理最优安排的非线性模型�这样既使得乘客所受影响达到最少�也便于飞机调整�还有利于飞机回到原来的航线�同时还在决策时间上对模型进行了优化和调整。
本文不仅一般性地将不相撞的问题转化为欧式距离控制�而且很巧妙的将不碰撞条件转化成简单的二次函数标准形式进行含参讨论�建立一个只含有转向角变量的模型。
并且再次很妙的具体化区域内受控时间形成矩阵�大大得简化运算�节约了大量运算的时间�便于管理人员控制操作�从而确保飞机的安全。
更重要的是最后结合实际缩短了搜索区间�并优化算法�使得决策更加高效。
最后的延时检验也充分体现了模型的可靠性。
关键字�欧氏距离约束转化缩短搜索区间时间矩阵延时检验1在约 10000 米的高空某边长为 160公里的正方形区域内�经常有若干架飞机作水平飞行。
区域内每架飞机的位置和速度向量均由计算机记录其数据�以便进行飞行管理。
当一驾欲进入该区域的飞机到达区域边缘时�记录其数据后�要立即计算并判断是否会与区域内的飞机发生碰撞。
如果会碰撞�则应计算如何调整各架�包括新进入的�飞机飞行的方向角�以避免碰撞。
现假定条件如下�公里以上�1�不碰撞的标准为任意两架飞机的距离大于 8公里�2�飞机飞行方向角调整的幅度不应超过 30度�3�所有飞机飞行速度均为每小时 800公里�4�进入该区域的飞机在到达区域边缘时�与区域内飞机的距离应在 605�最多需考虑 6架飞机�6�不必考虑飞机离开此区域后的状况。
请算你�对方这向个角误避差免不碰超撞过的飞0.机01管理问题建立数学模型�列出计算步骤�对以下数据进行计度��要求飞机飞行方向角调整的幅度尽量小。
设该区域内 4 个顶点的坐标为(0,0),(160,0),(160,160),(0,160)。
飞行管理问题数学模型

飞行管理问题以各飞机调整的飞行角度平方和作为目标函数,而以每两架飞机之间的最小距离不超过8公里,各飞机飞行角度调整的值不超过30o ,为约束条件。
如此得出的是一个非线性模型。
以t 表示时间;i x 与i y 分别表示第i 架飞机的横纵坐标(问题中已经给出);i θ表示第i 架飞机的飞行方向角(问题中已经给出);)(t d ij 表示t 时刻第i 架飞机与第j 架飞机间的距离;v 表示飞机的飞行速度(v = 800)。
则目标函数为:∑=∆=612i if θ。
)(2t d ij = 2))cos()(cos((j j i i j i vt x x θθθθ∆+-∆++-2))sin()(sin((j j i i j i vt y y θθθθ∆+-∆++-+, 则约束条件为:=ˆij D j i j i t d ij t ≠=>≥,6,,1,,64)(min 2。
⇒=02dtdd ij =t -a b ,其中a x x y y i j i i j j i j i i j j =-+-++-+-+()(cos()cos())()(sin()sin())θθθθθθθθ∆∆∆∆,b v i i j j i i j j =+-+++-+[(cos()cos())(sin()sin())]θθθθθθθθ∆∆∆∆22。
将t 代入即可求出ij D 。
于是本问题的一个数学模型为: ⎪⎪⎪⎩⎪⎪⎪⎨⎧≠=≤∆>∆=∑=ji j i D t s f i ij i i,6,,1,6||64..min 612πθθ,引入记号:T),,(61θθθ∆∆=∆ ,Tg g g ),,(151 =(g 是由64-ij D 按j i j i ≠=,6,,1, 构成的向量,在下面的程序中计算),则模型为:⎪⎩⎪⎨⎧≤≤<=vub vlb g t s f θθθ0..'min (10.1)其中TTvub vlb )1,1,1,1,1,1(6,)1,1,1,1,1,1(6ππ=-=。
35-36 案例:一个飞行管理问题

2)飞机方向角调整地幅度不应超过30度;
3) 所有飞机飞行速度均为每小时为800km;
4) 进入该区域的飞机在到达区域边缘时与区域内
飞机的距离应该在60km以上; 5) 最多需考虑6架飞机; 6) 不必考虑飞机离开此区域后的状况。
Department of Mathematics
HUST
Mathematical Modeling
Department of Mathematics
HUST
案例2:一个飞行管理问题
Mathematical Modeling
Release1.0
模型的假设说明
4.虽然假设2给出的调整范围为30度,但实
践证明,10度的调整范围就已足够(从
后面的模型1也可看出,即使两机相向
飞行,各自所需的调整也不超过8度),
ai
V
yij
Cij
飞机速度
Sij xij f
p( X , r )
sin ai sin a j xi x j
偏差平方和函数 罚函数
cos ai cos a j
yi y j
n
hij ( x)
( xi 0 , yi 0 ) 第i架飞机的坐标
求精次数 关于第i架飞机的等式约束
min D(ai , a j ) i, j 两机预计最短距离
运用非线性规划的方法提供了条件。非线性规划 如果求解时间在 2、3分钟以上将失去任何实际意义。 至少能在较短的时间内得到一 个较好的可行解 的算法种类繁多,但均只适用于某些类型的问题。 我们将求解时间上限定为 0.5分,以符合实际的要求。 由于缺乏适用的计算机软件包,我们自行编写实 现算法的程序。 综合程序准备时间和收敛速度两方面因素我们选择 了SUMT(序列无约束最小化方法)算法。
《运筹学》课程设计报告

《运筹学》课程设计报告姓名:班级:学号:一、问题描述1、机型指派问题众所周知,机型指派优化设计是航空公司制定航班计划的重要内容,它要求在满足航班频率和时刻安排以及各级型飞机总数的约束条件下,将各级型飞机指派给相应的航班,使运行成本最小化。
本课程设计就是通过建立机型指派问题的数学模型,并应用优化软件Lindo/Lingo进行建模求解,同时给出决策建议,包括各机型执行的航班子集和相应的运行成本。
2、问题描述已知某航空公司航班频率和时刻安排如《运筹学课程设计指导书》中表1所示,航班需求数据和运输距离如表2所示,其中,OrignA/P表示起飞机场,Dep.T.表示起飞时间,Dest.A/P表示目标机场,Dist表示轮挡距离,Demand表示航班需求量,Std Dev.表示需求的标准差。
该航空公司的机队有两种机型:9架B737-800,座位数162;6架B757-200,座位数200。
飞八个机场:A, B, I, J, L, M, O, S.B737-800的CASM(座英里成本)是0.34元,B757-200是0.36元。
两种机型的 RASM(座英里收益)都是 1.2元。
以成本最小为目标进行机型指派,在成本方面不仅考虑运行成本,还必须考虑旅客溢出成本,否则将偏向于选取小飞机,使航空公司损失许多旅客。
旅客溢出成本是指旅客需求大于航班可提供座位数时,旅客流失到其他航空公司造成的损失。
旅客需求服从N(μ,σ)的正态分布。
如果机票工作做得好,溢出旅客并不全部损失,有部分溢出旅客将该成本航空公司其他航班,这种现象叫做“再获得(Recapture)”。
设有15%的溢出旅客被再获得。
将飞机指派到航班上去,并使飞机总成本最小。
二、分析建模1.目标函数以成本最小为求解目标。
该成本包括两个部分,第一是运输成本,其表达式为:机型1的架数*每架座位数*座英里成本*该航班的飞行距离+机型2的架数*每架座位数*座英里成本*该航班的飞行距离;第二个为旅客溢出成本,表达式为:机型1旅客溢出的期望值*机型1的架数*机型1的座英里收益*该航班的飞行距离*0.85+机型2旅客溢出的期望值*机型2的架数*机型2的座英里收益*该航班的飞行距离*0.85。
《飞行管理问题》课件

飞行管理问题PPT课件大纲
简介
飞行管理是飞行中不可或缺的一环。了解飞行管理系统的需求和常见问题。
飞行管理
飞行管理是指对飞行活动进 行组织、协调和控制的过程。
飞行管理系统的需求
飞行管理系统可以提高飞行 效率、确保飞行安全、提升 航空公司的形象。
飞行管理常见问题
了解飞行管理中经常出现的 问题,为解决这些问题提供 参考。
2
操作规范执行
严格遵守操作规范,确保飞行操作的一致性和安全性。
3
机组人员培训
进行全面的机组人员培训,提高飞行操作的专业水平。
飞行数据记录
介绍飞行数据采集、存储和分析的重要性。
1
数据采集
使用专业工具和设备采集飞行数据,准确记录飞行过程中的各项参数。
2
数据存储
建立可靠的数据存储系统,确保数据的安全存储和使用。
3
数据分析
通过数据分析,发现飞行中的潜在问题和改进空间,提升飞行质量。
飞行安全控制
说明紧急事件响应、安全飞行培训和安全操作评估的重要性。
1
紧急事件响应
建立快速响应机制,处理突发紧急事件,确保乘客和机组人员的安全。
2
安全飞行培训
持续开展安全飞行培训,提高飞行人员的应急处置能力。
3
安全操作评估
定期对飞行操作进行评估,及时发现并解决安全风险问题。
详细介绍飞行计划的制定、通知和变更过程。
1
计划制定
根据航班需求和航空公司要求,制定详细的飞行计划。
2
计划通知
及时将飞行计划通知相关人员,确保信息准确无误。
3
计划变更
根据飞行需求的改变,及时更新飞行计划以保证飞行安全。
12.1一个飞行管理问题

在中国大学生数学建模竞赛(China undergraduate mathematical contest in modeling,CUMCM)中,曾经出现过大量的优化建模赛题.本章从中选择了部分典型赛题,举例分析其优化建模过程,说明如何应用LINDO/LINGO软件包求解这些赛题.12.1 一个飞行管理问题12.1.1 问题描述1995年全国大学生数学建模竞赛中的A题(“一个飞行管理问题”).在约10000m高空的某边长为160km的正方形区域内,经常有若干架飞机作水平飞行.区域内每架飞机的位置和速度向量均由计算机记录其数据,以便进行飞行管理.当一架欲进入该区域的飞机到达区域边缘时,记录其数据后,要立即计算并判断是否会与区域内的飞机发生碰撞.如果会碰撞,则应计算如何调整各架(包括新进入的)飞机飞行的方向角,以避免碰撞.现假定条件如下:(1)不碰撞的标准为任意两架飞机的距离大于8km;(2)飞机飞行方向角调整的幅度不应超过30°;(3)所有飞机飞行速度均为800km/h;(4)进入该区域的飞机在到达该区域边缘时,与该区域内的飞机的距离应在60km以上;(5)最多需考虑6架飞机;(6)不必考虑飞机离开此区域后的状况.请你对这个避免碰撞的飞行管理问题建立数学模型,列出计算步骤,对以下数据进行计算(方向角误差不超过0.01°),要求飞机飞行方向角调整的幅度尽量小.设该区域4个顶点的坐标为(0,0),(160,0),(160,160),(0,160).记录数据见表12-1.试根据实际应用背景对你的模型进行评价和推广.12.1.2 模型1及求解模型建立这个问题显然是一个优化问题.设第i架飞机在调整时的方向角为(题目中已经给出),调整后的方向角为=+(=1,2,…,6).题目中就是要求飞机飞行方向角调整的幅度尽量小,因此优化的目标函数可以是. (1)为了建立这个问题的优化模型,只须要明确约束条件就可以了.一个简单的约束是飞机飞行方向角调整的不应超过30°,即||30°. (2)题中要求进入该区域的飞机在到达该区域边缘时,与该区域内飞机的距离应在60km以上,这个条件是个初始条件,很容易验证目前所给数据是满足的,因此本模型中可以不予考虑.剩下的关键是要满足题目中描述的任意两架飞机不碰撞的要求,即任意两架位于该区域内的飞机的距离应大于8km.但这个问题的难点在于飞机是动态的,这个约束不好直接描述,为此我们首先需要描述每架飞机的飞行轨迹.记飞机飞行速率为v(=800km/h),以当前时刻为0时刻.设第i架飞机在调整时的位置坐标为(,)(已知条件),t时刻的位置坐标为(,),则=+,=+.如果要严格表示两架位于该区域内的飞机的距离应大于8km,则需考虑每架飞机在该区域内的飞行时间的长度.记为第i架飞机飞出去与的时刻,即=argmin{t>0:+=0或160,(4)或者+=0或160}. (5)记t时刻第i架飞机与第j架飞机的距离为(t),并记(t)=-64,这时在该区域内飞机不相撞的约束条件就变成了(t)=-640(0t).其中=min{,}. (6)此外,经过计算,可以得到(t)=+-64=++,(7)其中=2vt,(8)=2[-(-)+, (9)=+-64. (10)所以,(t)是一个关于的二次函数,表示的是一条开口向上的抛物线.当=-/2,即t=-/4v(记为)时,函数(t)取最小值-/4+.注意到(0)=0(初始时刻不相撞),如果-/20(即0),则此时约束条件(5)一定成立,所以对约束条件(5)只需考虑以下两种可能情况:如果0且,只需要(t)在右端点的函数值非负即可,即()0;(11)如果0且0,只需要(t)的最小值()=-/4+0即可,即40. (12)实际上,约束(11)表示的是(t)在右端点的函数值非负,这个约束在(12)的条件下也是自然成立的,所以可以对约束(11)不再附加0且的条件.于是,我们的模型就是; (13)S.t.||30°,(14)()0 (15)40.(当0且0). (16)模型求解上面这是一个非线性规划模型,虽然是严格满足题目要求的模型,但得到的模型逻辑关系比较复杂,约束(16)是在一定条件下才成立的约束,而且其中的计算式(4)也是含有相当复杂的关系式,使用LINGO软件不太容易将模型很方便地输入,因为逻辑处理不是LINGO的优势所在.即使能想办法把把这个模型输入到LINGO,也不一定能求出好的解(笔者尝试过,但LINGO运行时有时会出现系统错误,可能是系统有漏洞,无法继续求解).而且,在实时飞行调度中显然需要快速求解,所以下面我们想办法简化模型.这个模型麻烦之处就在于,要求严格表示两架位于该区域内的飞机距离应大于8km,所以需要考虑每架飞机在该区域内的飞行时间,比较繁琐.注意到区域对角线的长度只有160km,任何一架飞机在所考虑的范围内停留的时间不会超过=160/800=0.20.283(h),因此这里我们简化一下问题:不再单独考虑每架飞机在该区域停留的时间,而以最大时间(这里已经是一个常数)代替之,此时所有=.这实际上强化了问题的要求,即考虑了有些飞机可能已经飞出该区域,但仍不允许两架飞机的距离小于8km.这个简化的模型可以如下输入LINGO软件:MODEL:TITLE飞行管理问题的非线性规划模型;SETS:Plane/1..6/: x0, y0, cita0, cita1, d_cita;! cita0表示初始角度,cita1为调整后的角度,d_cita为调整的角度;link(plane, plane)|&1 #LT# &2: b,c;ENDSETSDATA:cita0 =max_cita = 30;T_max = 0.283;V=800;ENDDATAINIT:d_cita = 0 0 0 0 0 0;ENDINIT@for(plane: cita1 - cita0 = d_cita);@for(link(i,j):b(i,j) = -2*(x0(i) -x0(j))*@sin ((cita1(i)+cita1(j))*3.14159265/360) +2*(y0(i) -y0(j))*@cos ((cita1(i)+cita1(j))*3.14159265/360);c(i,j) = (x0(i) -x0(j)) ^2 + (y0(i) -y0(j)) ^2 - 64;);! 避免碰撞的条件;! 右端点非负;@for(link(i,j): [Right] (2*V*T_max*@sin((cita1(i)-cita1(j))*3.14159265/360))^2 + b(i,j)*(2*V*T_max*@sin((cita1(i)-cita1(j))*3.14159265/360)) + c(i,j) > 0);! 最小点非负;@for(link(i,j): [Minimum] @if(b(i,j)#lt#0 #and#-b(i,j)/4/V/@sin((cita1(i)-cita1(j))*3.14159265/360) #gt#0 #and#-b(i,j)/4/V/@sin((cita1(i)-cita1(j))*3.14159265/360)#lt#T_max ,b(i,j)^2-4*c(i,j),-1) < 0);!@for(link(i,j): @if(b(i,j)#lt#0, b(i,j)^2-4*c(i,j), -1) < 0);@for(link: @free(b));!调整角度上下限,单位为角度;@for(plane: @bnd( - max_cita, d_cita, max_cita));[obj] MIN = @SUM(plane: (d_cita)^2);![obj] MIN = @SUM(plane: @abs(d_cita));END注意:上面的模型中的方向角单位一律用角度,而LINGO只接受弧度,所以程序中一律进行了转换.求解这个模型,得到Local optimal solution found.Objective value: 295.4937Model Title: 飞行管理问题的非线性规划模型Variable Value Reduced CostD_CITA(1) -10.5.980 0.000000D_CITA(2) 0.000000 0.000000D_CITA(3) 0.000000 0.000000D_CITA(4) 6.515425 0.000000D_CITA(5) 10.00681 0.000000D_CITA(6) 6.505425 0.000000这个结果得到的是一个局部极小点,调整角度较大.能找到更好的解吗?如果不用全局求解程序,通常很难得到稍大规模的非线性规划问题的全局最优解.所以我们启动LINGO全局求解程序求解这个模型,可以得到全局最优解如下: Global optimal solution found at iteration: 93Objective value: 6.953944Model Title: 飞行管理问题的非线性规划模型Variable ValueD_CITA(1) 0.2719480E-02D_CITA(2) 0.5613433E-02D_CITA(3) 2.059140D_CITA(4) -0.4985421D_CITA(5) -0.5407837E-03D_CITA(6) 1.570129(这里只给出的值)可以看到,在0.01°的误差要求下,需要调整第3,4,6三架飞机的角度,分别调整2.06°,-0.50°,1.57°.调整量的平方和为6.95.其实,使用全局求解程序,通常也不一定要等到得到全局最优解,而是观察求解状态窗口,看到一个较好的当前解(或当前最好解在较长时间内不发生变化)时,就可以终止程序,用当前最好的局部最优解作为最后的恶结果.列如,对于本列,LINGO求出全局最优解大约需要1min,而实际上5s内LINGO就得到了与全局最优解类似的解.此外,上面的模型还可以进一步简化,列如可以假设要求飞机永远不相撞,即认为为无限大,这时显然约束(15)也是多余的,而且约束(16)中只需要0的条件就可以了.也就是说,上面的程序中的对应部分(约束[Right]和[Minimum])可以改写为更简单的形式:!有端点非负,不再需要;!最小点非负,简化为以下形式;@for(link(i,j): @if(b(i,j)#lt#0,b(i,j)^2-4* c(i,j),-1)0);实际计算显示,此时得到的结果与前面计算的结果几乎没有差别.备注优化的目标函数除了外,也可以设定为或等,用LINGO求解的过程是完全类似的,计算结果略有差异,这里就不再对两个目标函数具体计算了.甚至可以考虑让参与调整的飞机的数量尽量小,这种想法在实际中也不能说没有道理,但与题目中的要求不符,而且解题难度并没有减小,意义似乎不大.实际调度中,由于计算上面的调度方案需要时间,将调度信息告诉飞机驾驶员并作出调整方向角的操作也需要时间,因此如果考虑一定的反应滞后时间,应该是比较合理的.也就是说,如果反应时间是10s,则计算式中应采用飞机沿当前的方向角飞行10s以后的位置作为计算的基础.12.1.3 模型2及求解从12.1.2节可以看出,求解模型1的非线性规划模型是比较困难的,输入后也很可能找不到好的解甚至出现错误.此外,演示版软件还会受到求解规模的限制,尤其可能无权使用全局求解程序.因此,如果能把这个问题简化成比较简单的规划模型,将是非常有价值的.模型建立如图12-1,把两架飞机i,j分别看成半径为4km的圆(图中i,j为圆心),AB,CD为公切线,将AB和CD的夹角的一半称为碰撞角.在调整时刻,第i架飞机与第j架飞机的碰撞角为,则易知=),(17)其中为当前这两架飞机连线的长度(距离)图12-1 第i架飞机与第j架飞机的碰撞角因为飞机间的距离大于8km就不会相撞,所以这两个圆随着时间的推移不相交就可以了.为此,考虑第i架飞机相对于第j架飞机的相对速度(矢量,图中记为)是比较方便的,因为相对速度的大小和方向在飞机飞行中会始终保持不变(除非调整飞行角度).设为调整前的相对速度与这两架飞机连线(从i指向j的矢量)的夹角(以连线矢量为基准,逆时针方向为正,顺时针方向为负),则=-,具体来说,应该如下计算:=相对速度的辐角-从i指向j的连线矢量的辐角=-,). (18)注意:标准的反正切函数的符号是,返回主值;我们这里使用表示一个特殊的返回象限辐角的反正切函数,即返回向量(a ,b )的-到之间辐角(或者返回0到2之间的辐角也是可以的).即使这样,也还不能完全满足要求,因为这样得到的取值位于-2到2之间,还需要将它转换到-到之间才行(超过时就减去2,小于-就加上2).从图中可以看出(注意图中的两条辅助线n//CD 、m//AB ),两架飞机i ,j 不相撞的充要条件是(实际上不只是在所考虑的区域内不相交,而是永远不会相交)||.(19)如果调整前这个关系式成立,则不需要调整.否则,仍用表示第i 架飞机飞行方向角的调整量,并记由此引起的的改变量为.现在,问题的关键是如何弄清楚如何随和变化.可以证明=(+)/2.(20)下面利用复数的知识证明式(20)证明 由题知800i v Km A ==.设改变前的速度分别为'',jii i i j v Ae v Aeθθ==,改变方向后速度分别为()2i i i iv A eθθ+∆=,()2jji j v A eθθ+∆=改变前相对速度''j i i i ij i j v v v A e e θθ⎡⎤=-=-⎣⎦,改变后相对速度''j i i i ij i j v v v A e e θθ⎡⎤=-=-⎣⎦()()'22jjii i i ij i j v v v A e eθθθθ+∆+∆⎡⎤=-=-⎢⎥⎣⎦,()()'j j i i j ii i iji i ijA e evv A e eθθθθθθ+∆+∆⎡⎤-⎢⎥⎣⎦=⎡⎤-⎣⎦()()()()s ins inc o ss inc o s s in c o s s in i i i ijjjji i jji i i i θθθθθθθθθθθθ+∆++∆-+∆-+∆=+--()2sin sin cos 2222sin sin cos 222i i j j i i j j i i j j i j i j i j i i θθθθθθθθθθθθθθθθθθ+∆-+∆+∆-+∆+∆++∆⎛⎫- ⎪⎝⎭=-++⎛⎫- ⎪⎝⎭()2sin 2sin2i ji i j j i i jeθθθθθθθθ∆+∆⎛⎫⎪ ⎪⎝⎭+∆-+∆=-即'ij v 与ij v 辐角相差2i jθθ∆+∆.因此,可以得到如下的数学规划模型:(21)()1.. ,2ij ijij s t βθθα+∆+∆≥(22)30,1,6ii θ∆≤=…,(23)这仍然是一个非线性规划模型.同一样,这个模型中的+()12ij θθ∆+∆的取值也需要转换到-到之间才合理.通常情况下调整量很小,即(+)很小,因此只需要位于-到之间就差不多了(除非很接近-和,下面的表12-2显示本题并非这种情况). 模型求解为了编写LINGO 程序求解式(21)(23),必须解决如何用式(18)求的问题,因为21m in ;nii θ=∑,1,6,,i j i j =≠…,LINGO中并没有能返回-到之间的辐角的反正切函数.如果一定要用LINGO 求,就需要很仔细地利用LINGO中正常的@tan函数,通过判断每个点的位置,来正确得到这种关系,这是很不方便的,不是LINGO软件的优势所在.所以最好使用其他软件先计算以后直接输入LINGO.这里假设已经用其他方法(如MATLAB )计算得到了的值,如表12-2所示(由于对称性,只需要求出表中的一半元素的值).表12-2 其他方法计算得到了的值单位:(°)对于,由式(17)知它的取值位于0到/2之间,在反正切函数arcsin返回的角度的主值内,用LINGO计算也不麻烦,所以我们直接在LINGO中计算.于是,该飞机的数学规划模型可如下输入LINGO求解:MODEL:! 飞行管理模型;SETS:Plane/1..6/: x0, y0, d_cita;! d_cita为调整的角度;link(plane, plane)|&1 #LT# &2: alpha, beta;ENDSETSDATA:x0 y0 =150 14085 85150 155145 50130 1500 0 ;beta= 109.263642 -128.250000 24.179830 173.065051 14.474934-88.871097 -42.243563 -92.304847 9.00000012.476311 -58.786243 0.3108095.969234 -3.5256061.914383; ENDDATA! 计算alpha;@FOR(LINK(I,J): @SIN(alpha*3.14159265/180.0) =8 / ( (X0(I)-X0(J))^2 +(Y0(I)-Y0(J))^2 )^.5 );@for(link(i,j): @abs(beta(i,j) +0.5*d_cita(I)+0.5*d_cita(J))> alpha(I,J); );@for(link:@bnd(0,alpha,90));@for(plane: @bnd(-30,d_cita,30) );!min=@sum(plane: @sqr(d_cita));min=@sum(plane: @abs(d_cita) );END计算结果如下(只显示和的结果):Linearization components added:Constraints: 60Variables: 60Integers: 15Local optimal solution found at iteration: 575Objective value: 6.954676Variable Value Reduced Cost D_CITA(1) -0.2622117E-07 -0.1776357E-07 D_CITA(2) -0.249.247E-07 0.000000 D_CITA(3) 2.062448 0.000000 D_CITA(4) -0.4954375 0.000000 D_CITA(5) -0.2482437E-07 0.000000 D_CITA(6) 1.567011 0.000000 ALPHA(1,2) 5.391190 0.000000 ALPHA(1,3) 32.23095 0.000000 ALPHA(1,4) 5.091816 0.000000 ALPHA(1,5) 20.96336 0.000000 ALPHA(1,6) 2.234507 0.000000 ALPHA(2,3) 4.804024 0.000000 ALPHA(2,4) 6.613460 0.000000 ALPHA(2,5) 5.807866 0.000000ALPHA(2,6) 3.815925 0.000000ALPHA(3,4) 4.364672 0.000000ALPHA(3,5) 22.83365 0.000000ALPHA(3,6) 2.125539 0.000000ALPHA(4,5) 4.537692 0.000000ALPHA(4,6) 2.989819 0.000000ALPHA(5,6) 2.309841 0.000000这个结果与前面得到的结果几乎是一样的.注意上面显示结果的最前面几行,实际上是告诉我们LINGO对约束自动进行了线性化处理(“Linearization components added“),这是通过加入15个整数变量做到的(“Integers:15”).可见,对一些可以线性化的约束或目标(如这里的约束是变量线性函数的绝对值的形式的情行),LINGO具有自动线性化的功能,以便找到更好的解.应此,这时我们可以不用自己亲自对模型进行线性化(有时这是一件很困难的事情).事实上,我们看到此时不使用全局求解程序,就很容易得到了很好的解(不过由于目标还是非线性的,所以LINGO仍然只是报告了局部极小点).备注如果目标函数也采用绝对值和的形式,即|,则LINGO就能够自动实现整个模型线性化了.这只需将上面LINGO程序中的目标函数改写为:min=@sum(plane:@abs(d_cita));求解得到的显示为Linearization components added:Constraints: 84Variables: 84Integers: 21Global optimal solution found.Objective value: 3.629460Extended solver steps 7Variable Value Reduced CostD_CITA(1) 0.000000 0.000000D_CITA(2) 0.000000 0.000000D_CITA(3) 2.557886 0.000000D_CITA(4) 0.000000 0.000000D_CITA(5) 0.000000 0.000000D_CITA(6) 1.071574 0.000000由此可知最优解为 2.56°, 1.07°(其他调整角度为0).此时LINGO线性化时引入了21个整数解变量.由于转化后完全是(整数)线性规划模型,因此直接就可以得到全局最优解(不需要使用全局最优求解程序).需要指出的是,这个模型中的和+(+)的取值需要转换到-到之间才合理,对于一般情形的飞机初始位置,可能会有出现错误的时候,所以最好对最后求到的解进行一次可行性检验.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一个飞行管理问题模型2建立
在约10000m高空的某边长160km的正方形区域内,经常有若干架飞机作水平飞行,区域内每架飞机的位置和速度向量均由计算机记录其数据,以便进行飞行管理.当一架欲进入该区域的飞机到达边界区域边缘时, 记录其数据后,要立即计算并判断是否会与其区域内的飞机发生碰撞.如果会碰撞,则应计算如何调整各架(包括新进入的)飞机飞行的方向角,以避免碰撞.现假设条件如下:
1) 不碰撞的标准为任意两架飞机的距离大于8km;
2)飞机飞行方向角调整的幅度不应超过30度;
3)所有飞机飞行速度均为每小时为800km;
4)进入该区域的飞机在到达区域边缘时,与区域内飞机的距离应
在60km以上;
5)最多考虑6架飞机;
6)不必考虑飞机离开此区域后的状况;
对以下数据进行计算(方向角误差不超过0.01度),要求飞机飞行方向角调整的幅度尽量小.
飞机编号横坐标纵坐标方向角(度)
1 150 140 243
2 85 85 236
3 150 155 220.5
4 14
5 50 159
5 130 150 230
新进入0 0 52
注: 方向角指飞行方向与x轴正向的夹角
一、分析
在模型1的非线形规划模型是比较困难的,输入之后也很可能无权找不到好的解甚至出现错误,此外,演示软件还会受到求解规模的限制,尤其可能无权使用全局求解程序。
因此,如果能把这个问题简单化成简单的规划模型,将是非常有价值的。
下面就建立模型二。
二、模型的建立 如图1,把两架飞机i,j 分别看成半径为4km 的圆(图中i,j 为圆心),AB ,CD 为公切线,将AB 和CD 的夹角的一半称为碰撞角。
在调整时刻,设第i 架飞机与第j 架飞机的碰撞角为,则易知
其中r ij 为当前这两架飞机连线的长度(距离)。
因为飞机的距离大于8km 就不会相撞,所以如果这两个圆随着时间推移不相交就可以了。
为此,考虑第i 架飞机相对于第j 架飞机的相对速度(矢量,图中记为Vij )是比较方便的,因为相对速度的大小和方向在飞机飞行中会始终保持不变(除非调整飞行角度)。
社Bij 为调整前的相对速度Vij 与这架飞机连线(从i 指向j 的矢量)的夹角(以连线矢量为基准,逆时针方向为正,顺时针为负),则Bij=-Bji 。
具体来说,应该计算如下:
注意:标准的反正切函数的符号是arctan,返回主值;我们这里使用arctan2表示一个特殊的返回四象限辐角的反正切函数,即arctan2(b,a)返回向量
,
8
sin 1
ij
ij r -=α
(a,b )的-π到π之间的辐角(或者是返回0到 2π之间也是可以的)。
即使这样,也还能完全满足要求,因为这样的到ij β
图1:第i 架飞机与第j 架飞机的碰撞角
取值位于-2π到2π之间的,还需要将它转换到-π到π之间才行(超过π时就剪去2π,小于-π就加上2π)。
从图中可以看出(注意图中的两条辅助线in//CD 、im//AB ),两架飞机i ,j 不相撞的冲要条件是(实际上不只是在所考虑的区域内不相交,而是永远不相交)
|ij β|≥ij α
如果调整前这个关系式成立,则不需要调整。
否则,仍用i θ∆表示第i 架飞机飞
行方向角的调整量,并记由此引起的ij β的改变量∆ij β。
现在,问题的关键是如何弄清∆ij β如何和
i θ∆变化。
可以证明
下面利用复数的知识证明上式
证明
由题知| i v |=800km=A.设改变前的速度分别为'
i
v = i i e θA ,
'
j i j e θv =A ,改变方向后速度分别为
2
i
v =A ()
i i i e
θθ+∆ ,
2
j
v =A ()
j j i e
θθ+∆
改变前相对速度
ij v ='i v -'j v =A (i i e θ-j
j e θ
),
改变后相对速度
'
ij v =2
i v -2
i v =A [()i
i
i e θθ+∆- ()j
j
i e θθ+∆],
'
ij
ij v v =
()
()
[]
[]
j j i i j i
i i i i A e
e
A e e θθθθθθ+∆+∆--
= (
)
2
sin
2sin 2
i j
i i j j
i i j
e
θθθθθθθθ∆+∆+∆--∆-
即'ij v 和ij v 辐角相差2
i j
θθ∆+∆.
因此,可以得到如下的数学规划模型:
.
6,,1,
30,,6,,1,,
)(..216
1
2
=≤∆≠=≥∆+∆+∑=i j i j i t s Min i ij j i ij i i
θαθθβθ
参考文献:
[1] 谢金星薛毅,《优化建模与LINDO_LINGO软件》,北京:清华大学出版社,2005年
[2] 姜启源谢金星叶俊,《数学模型》(第三版),北京:高等教育出版社,2003年
[3] 朱道元,《数学建模案例精选》,北京:科学出版社,2003年。
