载流子浓度和电导率.
载流子浓度参考资料-霍尔系数法

霍尔系数和电阻率的测量把通有电流的半导体置于磁场中,如果电流方向与磁场垂直,则在垂直于电流和磁场的方向会产生一附加的横向电场,这个现象称为霍尔效应。
随着半导体物理学的发展,霍尔系数和电导率的测量已成为研究半导体材料的主要方法之一。
通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流子浓度、载流子迁移率等主要参数。
若能测量霍尔系数和电导率随温度变化的关系,还可以求出材料的杂质电离能和材料的禁带宽度。
一、实验目的1. 了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识;2. 学习用“对称测量法”消除副效应的影响,测量并绘制试样的V H -I S 和V H -I M 曲线;3. 确定试样的导电类型、载流子浓度以及迁移率。
二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子和空穴)被约束在固体材料中,这种偏转就导致在垂直于电流和磁场的方向上产生正负电荷的积累,从而形成附加的横向电场,即霍尔电场。
对于图2.1 (a)所示的N 型半导体试样,若在X 方向的电极D 、E 上通以电流I S ,在Z 方向加磁场B ,试样中载流子(电子)将受洛仑兹力:B v e F g (2.1)其中,e 为载流子(电子)电量,v 为载流子在电流方向上的平均定向漂移速率,B 为磁感无论载流子是正电荷还是负电荷,Fg 的方向均沿Y 方向,在此力的作用下,载流子发生偏移,则在Y 方向即试样A 、A ’电极两侧就开始聚集异号电荷,在A 、A ’两侧产生一个电位差V H ,形成相应的附加电场E H ——霍尔电场,相应的电压V H 称为霍尔电压,电极A 、A ’称为霍尔电极。
电场的指向取决于试样的导电类型。
N 型半导体的多数载流子为电子,P 型半导体的多数载流子为空穴。
对N 型试样,霍尔电场逆Y 方向,P 型试样则沿Y 方向,有I S (X)、B (Z) E H (Y) < 0 (N 型)E H (Y) > 0 (P 型)(a) (b) 图2.1 样品示意图显然,该电场是阻止载流子继续向侧面偏移。
半导体材料的载流子浓度与电导率

半导体材料的载流子浓度与电导率半导体材料是现代电子技术中不可或缺的基础材料之一,其载流子浓度与电导率是决定半导体器件性能的关键因素。
本文将讨论载流子浓度与电导率之间的关系以及影响载流子浓度和电导率的因素。
1. 半导体材料与载流子浓度半导体材料本质上是能带结构介于导体和绝缘体之间的材料。
在纯净的半导体中,载流子的浓度非常低,通常为每立方厘米10^6至10^9个。
货币开发载流子浓度的关键技术是掺杂,即在半导体材料中引入外来元素。
根据掺杂的不同,可以分为N型半导体和P型半导体。
N型半导体通过掺入少量五族元素如砷、磷等,引入多余的自由电子,这些自由电子称为N型半导体中的主要载流子。
载流子浓度增加,导电性能也会增加。
P型半导体通过掺入少量三族元素如硼、铝等,引入少量的空穴,这些空穴称为P型半导体中的主要载流子。
当载流子浓度增加时,导电性能也会增加。
2. 载流子浓度与电导率的关系载流子的浓度与半导体的电导率密切相关。
半导体材料中的载流子在电场的作用下会发生移动,导致电流的流动。
载流子密度增加,电导率也会相应增加。
载流子的浓度与电导率之间的关系可以用经典的“导电带模型”来解释。
导电带模型认为半导体材料的导电性质取决于电子能带结构。
对于N型半导体来说,载流子为自由电子,其晶格能带结构中价带和导带之间存在禁带。
在外加电场的作用下,电子从价带跃迁到导带,因此导电性能较好。
对于P型半导体来说,载流子为空穴,其导电性质也是类似的。
由于载流子浓度与电导率之间存在直接的正相关关系,所以在设计半导体器件时,可以通过掺杂技术调控载流子浓度来改变电导率。
这对于一些需要调节电导率的场合如场效应管、二极管等器件非常重要。
3. 影响载流子浓度和电导率的因素除了掺杂技术对载流子浓度和电导率的影响外,还有其他因素也会对其产生影响。
(1)温度:半导体材料的载流子浓度与温度呈反相关关系。
随着温度的升高,载流子的热激发增加,从而导致载流子浓度的增加,进而提高电导率。
载流子浓度参考资料-霍尔系数法
霍尔系数和电阻率的测量把通有电流的半导体置于磁场中,如果电流方向与磁场垂直,则在垂直于电流和磁场的方向会产生一附加的横向电场,这个现象称为霍尔效应。
随着半导体物理学的发展,霍尔系数和电导率的测量已成为研究半导体材料的主要方法之一。
通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流子浓度、载流子迁移率等主要参数。
若能测量霍尔系数和电导率随温度变化的关系,还可以求出材料的杂质电离能和材料的禁带宽度。
一、实验目的1. 了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识;2. 学习用“对称测量法”消除副效应的影响,测量并绘制试样的V H -I S 和V H -I M 曲线;3. 确定试样的导电类型、载流子浓度以及迁移率。
二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子和空穴)被约束在固体材料中,这种偏转就导致在垂直于电流和磁场的方向上产生正负电荷的积累,从而形成附加的横向电场,即霍尔电场。
对于图2.1 (a)所示的N 型半导体试样,若在X 方向的电极D 、E 上通以电流I S ,在Z 方向加磁场B ,试样中载流子(电子)将受洛仑兹力:B v e F g (2.1)其中,e 为载流子(电子)电量,v 为载流子在电流方向上的平均定向漂移速率,B 为磁感无论载流子是正电荷还是负电荷,Fg 的方向均沿Y 方向,在此力的作用下,载流子发生偏移,则在Y 方向即试样A 、A ’电极两侧就开始聚集异号电荷,在A 、A ’两侧产生一个电位差V H ,形成相应的附加电场E H ——霍尔电场,相应的电压V H 称为霍尔电压,电极A 、A ’称为霍尔电极。
电场的指向取决于试样的导电类型。
N 型半导体的多数载流子为电子,P 型半导体的多数载流子为空穴。
对N 型试样,霍尔电场逆Y 方向,P 型试样则沿Y 方向,有I S (X)、B (Z) E H (Y) < 0 (N 型)E H (Y) > 0 (P 型)(a) (b)图2.1 样品示意图显然,该电场是阻止载流子继续向侧面偏移。
本征半导体载流子

本征半导体载流子
1. 什么是本征半导体
本征半导体是指没有掺杂杂质的半导体材料,其电子与空穴的浓度完全相等。
由于在本征半导体中,电子与空穴的数量相等,因此其导电性质比较特殊,可以在外加电场或光照作用下发生电子与空穴的复合,产生电流。
2. 本征半导体的载流子
在本征半导体中,载流子主要包括电子和空穴。
电子是带负电的粒子,空穴是带正电的粒子。
在本征半导体中,电子和空穴的数量相等,因此其导电性质特殊。
3. 本征半导体的电导率
本征半导体的电导率是由其载流子浓度决定的。
在本征半导体中,电子浓度与空穴浓度相等,因此其电导率比较低。
但是,在外加电场或光照作用下,会产生电子与空穴的复合,从而增加载流子浓度,提高电导率。
4. 本征半导体的应用
本征半导体在半导体器件中有着重要的应用,如晶体管、太阳能电池等。
在晶体管中,本征半导体被用作基底材料,提供支撑和导电功能。
在太阳能电池中,
本征半导体则被用作光电转换材料,将光能转化为电能。
总之,本征半导体作为一种特殊的半导体材料,其载流子和电导率等性质与掺杂半导体有所不同,但在半导体器件中有着重要的应用。
载流子浓度参考资料-霍尔系数法

载流子浓度参考资料-霍尔系数法霍尔系数和电阻率的测量把通有电流的半导体置于磁场中,如果电流方向与磁场垂直,则在垂直于电流和磁场的方向会产生一附加的横向电场,这个现象称为霍尔效应。
随着半导体物理学的发展,霍尔系数和电导率的测量已成为研究半导体材料的主要方法之一。
通过实验测量半导体材料的霍尔系数和电导率可以判断材料的导电类型、载流子浓度、载流子迁移率等主要参数。
若能测量霍尔系数和电导率随温度变化的关系,还可以求出材料的杂质电离能和材料的禁带宽度。
一、实验目的1. 了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识;2. 学习用“对称测量法”消除副效应的影响,测量并绘制试样的V H-I S和V H-I M曲线;3. 确定试样的导电类型、载流子浓度以及迁移率。
二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子和空穴)被约束在固体材料中,这种偏转就导致在垂直于电流和磁场的方向上产生正负电荷的积累,从而形成附加的横向电场,即霍尔电场。
对于图2.1 (a)所示的N 型半导体试样,若在X 方向的电极D 、E 上通以电流I S ,在Z 方向加磁场B ,试样中载流子(电子)将受洛仑兹力:Bv e F g (2.1) 其中,e 为载流子(电子)电量,v 为载流子在电流方向上的平均定向漂移速率,B 为磁感应强度。
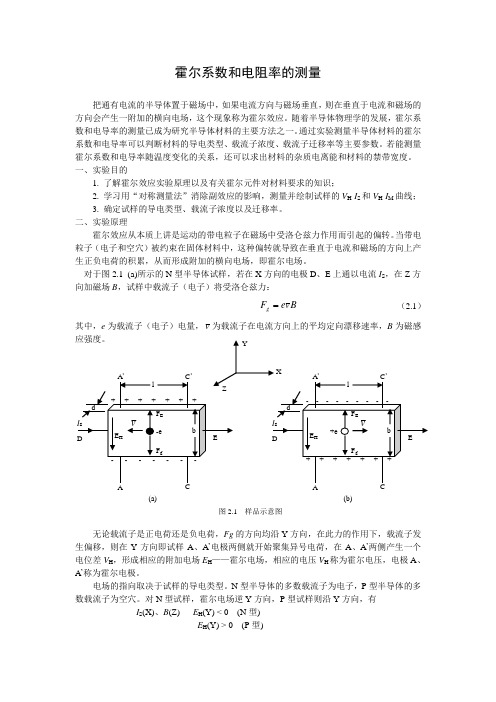
X YZ E D I S A C b l + + + + + + + + - - - - - - d F E F g v E H -e E D I S A C b l - - - - - - - - + + + + + + + + d F E F g v E H +e (a (b 图2.1 样品示意图无论载流子是正电荷还是负电荷,Fg的方向均沿Y方向,在此力的作用下,载流子发生偏移,则在Y方向即试样A、A’电极两侧就开始聚集异号电荷,在A、A’两侧产生一个电位差V H,形成相应的附加电场E H——霍尔电场,相应的电压V H称为霍尔电压,电极A、A’称为霍尔电极。
半导体物理期末复习知识要点汇编

一、半导体物理学基本概念有效质量-----载流子在晶体中的表观质量,它体现了周期场对电子运动的影响。
其物理意义:1)有效质量的大小仍然是惯性大小的量度;2)有效质量反映了电子在晶格与外场之间能量和动量的传递,因此可正可负。
空穴-----是一种准粒子,代表半导体近满带(价带)中的少量空态,相当于具有正的电子电荷和正的有效质量的粒子,描述了近满带中大量电子的运动行为。
回旋共振----半导体中的电子在恒定磁场中受洛仑兹力作用将作回旋运动,此时在半导体上再加垂直于磁场的交变磁场,当交变磁场的频率等于电子的回旋频率时,发生强烈的共振吸收现象,称为回旋共振。
施主-----在半导体中起施予电子作用的杂质。
受主-----在半导体中起接受电子作用的杂质。
杂质电离能-----使中性施主杂质束缚的电子电离或使中性受主杂质束缚的空穴电离所需要的能量。
n-型半导体------以电子为主要载流子的半导体。
p-型半导体------以空穴为主要载流子的半导体。
浅能级杂质------杂质能级位于半导体禁带中靠近导带底或价带顶,即杂质电离能很低的杂质。
浅能级杂质对半导体的导电性质有较大的影响。
深能级杂质-------杂质能级位于半导体禁带中远离导带底(施主)或价带顶(受主),即杂质电离能很大的杂质。
深能级杂质对半导体导电性质影响较小,但对半导体中非平衡载流子的复合过程有重要作用。
位于半导体禁带中央能级附近的深能级杂质是有效的复合中心。
杂质补偿-----在半导体中同时存在施主和受主杂质时,存在杂质补偿现象,即施主杂质束缚的电子优先填充受主能级,实际的有效杂质浓度为补偿后的杂质浓度,即两者之差。
直接带隙-----半导体的导带底和价带顶位于k空间同一位置时称为直接带隙。
直接带隙材料中载流子跃迁几率较大。
间接带隙-----半导体的导带底和价带顶位于k空间不同位置时称为间接带隙。
间接带隙材料中载流子跃迁时需有声子参与,跃迁几率较小。
平衡状态与非平衡状态-----半导体处于热平衡态时,载流子遵从平衡态分布,电子和空穴具有统一的费米能级。
实验三-霍尔效应法测量半导体的载流子浓度、-电导率和迁移

实验三霍尔效应法测量半导体的载流子浓度、电导率和迁移率一、实验目的1.了解霍尔效应实验原理以及有关霍尔元件对材料要求的知识。
2.学习用“对称测量法”消除副效应的影响,测量并绘制试样的 VH-IS 和VH-IM 曲线。
3.确定试样的导电类型、载流子浓度以及迁移率。
二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积,从而形成附加的横向电场,即霍尔电场。
对于图(1)(a)所示的 N 型半导体试样,若在 X 方向的电极 D、E 上通以电流 Is,在 Z 方向加磁场 B,试样中载流子(电子)将受洛仑兹力:其中 e 为载流子(电子)电量, V为载流子在电流方向上的平均定向漂移速率,B 为磁感应强度。
无论载流子是正电荷还是负电荷,Fg 的方向均沿 Y 方向,在此力的作用下,载流子发生便移,则在 Y 方向即试样 A、A´电极两侧就开始聚积异号电荷而在试样 A、A´两侧产生一个电位差 VH,形成相应的附加电场 E—霍尔电场,相应的电压 VH 称为霍尔电压,电极 A、A´称为霍尔电极。
电场的指向取决于试样的导电类型。
N 型半导体的多数载流子为电子,P 型半导体的多数载流子为空穴。
对 N 型试样,霍尔电场逆 Y 方向,P 型试样则沿Y 方向,有显然,该电场是阻止载流子继续向侧面偏移,试样中载流子将受一个与 Fg方向相反的横向电场力:其中 EH 为霍尔电场强度。
FE 随电荷积累增多而增大,当达到稳恒状态时,两个力平衡,即载流子所受的横向电场力 e EH 与洛仑兹力eVB 相等,样品两侧电荷的积累就达到平衡,故有设试样的宽度为 b ,厚度为 d ,载流子浓度为 n ,则电流强度V Is 与的 关系为由(3)、(4)两式可得即霍尔电压 VH (A 、A ´电极之间的电压)与 IsB 乘积成正比与试样厚度 d 成反比。
电导率和载流子浓度关系

电导率和载流子浓度关系1. 引言大家好,今天咱们聊聊电导率和载流子浓度的关系,这可是个有趣的话题哦!电导率,就像是电流在电路中流动的“顺畅程度”,而载流子浓度则是这些“流动的小伙伴”——电子和空穴的数量。
简单来说,如果载流子浓度高了,电导率也会跟着蹭蹭上涨,就像一条河流里的水越来越多,流速自然也会加快。
你有没有想过,为什么这个关系如此紧密呢?嘿,别着急,咱们慢慢来聊。
2. 电导率的基础2.1 什么是电导率?电导率,简单来说,就是电流通过材料的能力。
想象一下,电流就像一群小鱼在河里游,电导率就是河流的宽度和深度,河流越宽越深,小鱼游得越快,电流也就越大。
电导率的单位是西门子(S),有点像把电流和电压的关系压缩成一个数字,越大越好!2.2 载流子浓度的角色那载流子浓度呢?这就像是河里游的小鱼的数量。
载流子一般是电子和空穴,电子就像是带着游泳圈的小鱼,空穴则是鱼群中的空位。
载流子浓度越高,意味着河里鱼越多,电流就能更轻松地通过。
相反,如果小鱼少了,电流就会变得稀稀拉拉,游得慢吞吞的。
3. 电导率和载流子浓度的关系3.1 直接关系电导率和载流子浓度的关系可以用一个简单的公式表示:σ = n * q * μ。
这其中,σ是电导率,n是载流子浓度,q是载流子的电荷量,而μ是它们的迁移率。
听上去复杂,其实就是说明了,载流子浓度越高,电导率就越大。
就像人多热闹一样,电流在载流子间的“舞蹈”也变得更加灵活,流动得更快。
3.2 温度的影响不过,这里有个小插曲,温度也会影响这个关系哦。
当温度升高时,载流子的运动速度会加快,电导率也会因此提高。
但是,别以为温度一高就好,某些材料在高温下可能会出现更多的缺陷,反而导致电导率下降。
就像人热了出汗,反而影响了运动状态一样。
4. 应用实例4.1 半导体的应用在半导体中,这种关系显得尤为重要。
我们常常会看到,随着掺杂浓度的增加,电导率也在攀升。
这就像是在一场派对上,客人越多,气氛越热烈!但如果过了头,反而可能让派对变得混乱,电导率也会有所下降。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ni 2 (1.5 1010 )2 16 3 n3 1 10 cm p3 2.25 104
( 2)
p 型半导体. p02 n02 , 即 ni n01 p01 1.51010 cm3 ,故为本征半导体. p01 n02 ,即 2.25 104 11016 cm3 ,故为 n 型半导体. (3).当 T=300k 时, k T 0.026eV 由
m
e dn mdp
3/ 4
( mdn mdp ) T
3/ 4
3/ 2
e
Eg 2 kT
2. 影响 ni 的因素 (1) mdn、mdp、Eg (2) T 的影响
——材料
Eg 1 3 ln ni A ln T 2 2k T
T↑,lnT↑,1/T↓,ni↑
高温时,在 ln ni~ 1/T 坐标下, 近似为一直线。
Ei EF p ni e x p ( kT )
p01 n01 即 2.25 1016 1104 cm3 ,故为
得: 对三块材料分别计算如下:
p Ei EF k T ln ni
(ⅰ) 即 p 型半导体的费米能级在禁带中线下 0.37eV 处。
10 3
p 2.25 1016 Ei EF k T ln 0.026ln 0.37(eV ) 10 ni 1.5 10
EF Ei n ni e x p ( kT )
p 2.25 1016 Ei EF k T ln 0.026ln 0.37(eV ) 10 ni 1.5 10
n 1016 EF Ei k T ln 0.026ln 0.35(eV ) ni 1.5 1010
得: 对三块材料分别计算如下:
Ei EF k T ln
p ni
(ⅰ) 即 p 型半导体的费米能级在禁带中线下 0.37eV 处。 10 3 Ei EF 0 n p n 1.5 10 cm (ⅱ) 02 02 i 即费米能级位于禁带中心位置。 (ⅲ)对 n 型材料有
假设参杂原子全部电离,上式变为:
p - n - NA + ND =0
由np乘积关系可得
p
ni
2
n
ni
2
2
n
n ND N A 0
2
n n( ND N A ) ni 0
解得
ND N A ND N A 2 2 n ( ) ni 2 2
二、本征载流子浓度及影响因素
1. 本征载流 子浓度 ni
no p0 N c NV e no po ni N C NV e
2 Eg kT Eg 2 kT Eg 2 kT Eg kT
ni N C NV e
1/ 2
2kT 2 2 h
3/ 2
∴po = NA
n n n0 po N A
2 i
2 i
三、本征半导体在应用上的限制
●纯度达不到
本征激发是载流子的主要来源
(杂质原子/总原子 << 本征载流子/总原子) Si:原子密度 1023/cm3,室温时,ni =1010/cm3 本征载流子/总原子=1010/1023=10-13> 杂质原子/总原子 要求Si的纯度必须高于99.9999999999999%!
10 3 E 1.12 ev n 1.5 10 cm g (1)室温时硅的 , i
根据载流子浓度积公式:
ni 2 n 2 n p ni 可求出 p ni 2 (1.5 1010 )2 4 3 n1 1 10 cm p 1 2.25 1016 ni 2 (1.5 1010 )2 10 3 n2 1.5 10 cm p2 1.5 1010 ni 2 (1.5 1010 )2 16 3 n3 1 10 cm p3 2.25 104
NA
(3)掺杂半导体(ND-NA<<ni或NDNA<<ni)
n p ni
(4)补偿半导体
ND和NA是可比的但是不相等,这种 材料称为补偿半导体。
●本征载流子浓度随温度变化很大
在室温附近:
Si: T ↑, 8K ni↑ 一倍 Ge: T ↑, 12K ni↑ 一倍
●本征半导体的电导率不能控制
四、杂质半导体载流子浓度和费米能级
带电粒子有: 电子、空穴、电离的施主和电离的受主 电中性条件(平衡条件下):
p - n - NA- + ND+ =0
即对 n 型材料,费米能级在禁带中心线上 0.35eV 处。
应用
Байду номын сангаас
n 型半导 体 在常温下,已知施主浓度 ND,并且全部电离, 求导带电子浓度 no 和价带空穴浓度 po ∵ 施主全部电离 ∴ no= ND
n n p0 no N D
2 i
2 i
P型半导体
在常温下,已知受主浓度 NA,并且全部电 离,求导带电子浓度 no 和价带空穴浓度 po ∵ 受主全部电离
1/ 2
N A ND N A ND 2 2 p ( ) ni 2 2
1/ 2
讨论:
(1)本征半导体
n p ni
(2)掺杂半导体(ND-NA>>ni或 NA-ND>>ni)
n型半导体:n N D, p
p型半导体:p N A, n ni
2
n i2 ND
3. 杂质半导体载流子浓度积与 ni 关系
no p0 Nc NV e
Ec EF kT
e
EF Ev kT
Nc NV e
Eg kT
no po n
2 i
强调:不仅适用于本征半导体材料,也 适用于非简并的杂质半导体材料。
例、 现有三块半导体硅材料,已知室温下(300K) 它们的空穴浓度分别为:
p02 1.5 1010 cm 3 , p03 2.25 104 cm 3 。 p01 2.25 1016 cm 3
,
(1) 分别计算这三块材料的电子浓度 n01 , n02 , n03 ; (2) 判断这三块材料的导电类型; (3) 分别计算这三块材料的费米能级的位置。
