高中数学:用补形法解立体几何题
巧用补形法解决立体几何问题

体或置于一个更熟悉的几何体中,巧妙地破解空间几何体的体积等问
题,常见的补形法有对称补形、联系补形与还原补形,对于还原补形,
主要涉及台体中“还台为锥”.
(2)补形法的应用条件:当某些空间几何体是某一个几何体的一部分, 且求解的问题直接求解较难入手时,常用该法.
【类题试解】如图所示,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E
3 2 6 AH= 3 ,在△AFG和△AHO中,根据三角形相似可知 1-( ) , 3 3 3 3 3 AG AH 6 外接球的表面积S球= 4( 6 ) 2 3 . 2 3 OA . 4 2 AF 4 6 3 答案: 3 2
2
【巧妙解法】由已知条件知,平面图形中AE=EB=BC=CD=DA=DE=EC=1.
折叠后得到一个正四面体.如图所示,把正四面体放在
正方体中,显然,正四面体的外接球就是正方体的外接 球.因为正四面体的棱长为1,所以正方体的棱长为 2 , 所以外接球直径2R= 3 2 ,所以R= 6 ,
4 所以外接球的表面积S球= 4( 6 )2 3 . 4 2 答案: 3 2 2 2
所以V几何体=V三棱柱+V四棱锥.
由题知三棱柱ABC-NDM的体积为
V1= 1 ×8×6×3=72.
2
四棱锥D-MNEF的体积为:
1 1 1 V2 S梯形MNEF DN 1 2 6 8 24, 3 3 2
则几何体的体积为:V=V1+V2=72+24=96.
答案:96
【巧妙解法】用“补形法”把原几何体补成一个直三 棱柱,使AA′=BB′=CC′=8, 所以V几何体= 1 V三棱柱= 1 ×S△ABC·AA′=
巧用补形法研究四面体问题
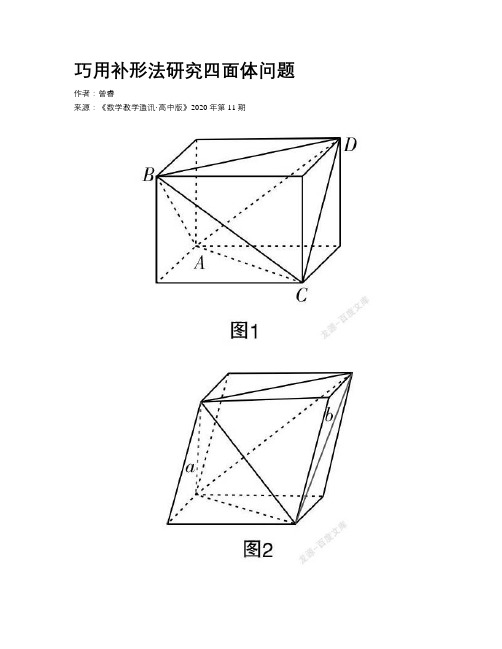
巧用补形法研究四面体问题作者:***来源:《数学教学通讯·高中版》2020年第11期[摘要] 立体几何问题中,有一类问题可以通过补形法,得到一个常见的几何体,使复杂的线面关系变得清晰明了. 文章从一道例题出发分析解决这类问题的方法,并在此基础上总结规律,归纳常见的一些四面体的补形方法.[关键词] 立体几何;四面体;补形教学中,遇到这样一个问题:已知在半径为2的球面上有A,B,C,D 四点,若AB=CD=2,则四面体ABCD的体积最大值为多少?这是某年数学全国卷的第12题,主要考查几何体的体积的计算、球的性质、异面直线间的距离,通过球这个载体考查学生的空间想象能力和推理计算能力.解答是这样的:过CD作平面PCD,使AB垂直于平面PCD,交AB于P. 设点P到CD的距离为h,则有V■=■×■×2×h×2=■h,当直径通过AB与CD中点时,h■=2■=2■,故V■=■.本小题这个解答当中,学生比较疑惑的有两点:(1)为什么可以过CD作平面PCD,使AB垂直于平面PCD,能这样作的前提是AB和CD要垂直,那为什么认定体积最大时AB和CD要垂直?(2)为什么直径通过AB与CD中点时,距离h最大?要解释清楚这两个疑点,首先需要补充说明一个公式.四面体体积公式:如果一个四面体的两条相对棱的长分别是a,b,它们的距离为d,所成的角为θ,那么它的体积为V■=■abdsinθ(证明见后).根据这个公式,我们首先得到结论:AB和CD必须垂直,即sinθ=90°时才能得到最大的体积.其次,由于AB=CD=R(球的半径),所以连结球心O和四个顶点,则容易知道△OAB 和△OCD都是正三角形.设AB的中点为E,CD的中点为F,则OE⊥AB,OF⊥CD.设AB与CD间的距离为d,有d≤EF≤OE+OF. (异面直线间公垂线段最短)因此,OEF共线时,四面体的体积可以达到最大值,因为OE=OF=■,故V■=■.?摇?摇这样解决一个选择题比较花费时间,而且在高中数学教学中,不涉及四面体的体积公式,异面直线的距离即公垂线段的长度在教学中也仅仅要求了解.下面我们用补形的思路来解决这个问题.因为题目当中两条线段长度一样,所以考虑把这个四面体补形成一个长方体:如图1:则四面体的外接球即是长方体的外接球,四面体的体积是长方体的体积减去四个全等的小三棱锥的体积.设长方体的边长为a,b,c,体对角线即为外接球的直径,得到:a2+b2+c2=42,b2+c2=22,所以a=2■,则V■=V■-4V■=abc-4×■×■abc=■abc=■.又b2+c2=22 ,所以V■=■≤■(b2+c2)=■,当且仅当b=c=■时,等号成立.从等号成立的条件可以比较容易地看出是在AB和CD垂直时,四面体的体积取到了最大值.我们会发现,使用补形,一下子把陌生的几何体变得熟悉了,原本错综复杂的线面关系也变得清晰起来. 利用这一方法解决某些几何问题,思路清晰明朗,较其他方法简洁明了.比如刚才提到的四面体的体积公式也可以用补形法得到.一个四面体的两条相对棱的长分别是a,b,它们的距离为d,所成的角为θ,将四面体补形成平行六面体(因为相对棱的长度不确定,相等的时候才能补成长方体).如图2:那么该平行六面体的底面积为S=■absinθ,平行六面体的体积为V■=■abdsinθ. 同样,该平行六面体由原四面体和四个全等的三棱锥构成. 三棱锥与平行六面体的高相等,底面积为平行六面体的一半,V■=■×■×■absinθ=■absinθ.所以V■=V■-4×V■=■absinθ.一起来看一下常见的几种四面体补形方式:一、把四面体的四个面各补上一个三棱锥,最后形成一个平行六面体. 其中正四面体是最特殊的形式,可以补成正方体. 而对棱相等的四面体则可以补形成一个长方体.例1:正四面体棱长为a,求外接球的半径R.正四面体补形为一个正方体,正四面体的外接球即为正方体的外接球.如图3:正方体的面对角线是正四面体的棱长,体对角线为外接球的直径.设正方体边长为b,则a=■b,2R=■b,所以R=■a.例2:在三棱锥A-BCD中,AB=CD=3,AD=BC=4,AC=BD=5,求三棱锥A-BCD外接球的半径.因为有三组对棱相等,把四面体补成一个长方形,如图4:长方体的三个面的面对角线是三棱锥的棱长,体对角线是外接球的直径.设长方体的棱长为a,b,c,外接球的半径为R,则a2+b2=32,b2+c2=42,a2+c2=52,(2R)2=a2+b2+c2,所以R=■.二、把四面体的一个角作为平行六面体的一个角补形成平行六面体.例3:四面体ABCD,侧棱AB,AC,AD两两垂直,AB=2,AC=3,AD=4,求四面体的外接球的半径R.因为四面体的侧棱两两垂直,所以可以把这个角看作长方体的一个角,把四面体补形成一个长方体,则四面体的外接球就是长方体的外接球四面体的三条侧棱就是长方体的长、宽、高,外接球的直径就是长方体的体对角线,则(2R)2=AB2+AC2+AD2=29,所以R=■.例4:若三棱锥S-ABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2■,AB=1,AC=2,∠BAC=60°,求球O的半径R.根据已知条件可以得到△ABC是直角三角形,把四面体补成一个长方体,则四面体的外接球就是长方体的外接球,外接球的直径就是长方体的体对角线.则(2R)2=SA2+AC2=16,所以R=2.例5:已知四面体PABC的侧面PAC与平面ABC垂直,∠ABC=90°,BC=2■,AB=2,且PA⊥PC,PA=PC,求异面直线PC与AB所成角的余弦值.解答:把四面体补成如图所示平行六面体,异面直线PC与AB所成角即為PC与CD所成角的补角的余弦值.取AC中点M,PA=PC,则PM⊥AC,又因为平面PAC与平面ABC垂直,所以PM⊥平面ABC.△ABC中,∠ABC=90°,AB=2,BC=2■,所以∠ACB=30°,AC=4.△PAC中,PA⊥PC,PA=PC,AC=4,所以PM=2,PC=2■.底面四边形ABDC中,DM2=DC2+CM2-2DC·CM·cos120°,得到DM=2■.Rt△PMD中,PD=4.△PCD中,cos∠PCD=■= -■.所以异面直线PC与AB所成角的余弦值为■.此题也可以用空间向量法解答,用补形能更好地体现线面关系.三、把四面体补形成三棱柱例6:已知某几何体底面ABC是棱长为1的等边三角形,PA⊥平面ABC,PA=3,求该几何体的外接球的半径.解答:将该四面体补形成一个三棱柱四面体的外接球就是三棱柱的外接球.先求三棱柱底面三角形外接圆半径r=■·■=■.又因为PA⊥平面ABC,PA=3,所以三棱柱的外接球半径为R=■=■.四面体的问题可以通过补形变成正方体、长方体乃至平行六面体的问题.尤其在正方体和长方体中,点线面的关系是我们所熟悉的. 一些几何题的证明和求解,由原几何图形分析探究会比较烦琐,通过补形填补成一个新的几何图形,能使原问题的本质得到充分的体现,解决起来比较容易. 本文着重讨论四面体的补形问题,希望窥一斑而知全豹,探究立体几何中补形法这一重要的转化策略.。
补形巧解立体几何题

AD
=
1 2
,求面
SCD
与面
SAB
所成二面角的正切值.
解析 如图 13,延长 BA、CD 交于 E,连结 SE.
因为 AD
=
1 2
BC,且 AD ∥ BC,所以 EA
= AB
= SA
= 1,SE ⊥ SB.
又因为 SA ⊥ 面 ABCD,所以面 SEB ⊥ 面 ABCD,
因为 BC ⊥ EB,所以 BC ⊥ 面 SEB,BC ⊥ SE,
所以 SE ⊥ 面 SBC,SE ⊥ SC,∠BSC 是所求二面
角的平面角,又因为 SB = 2 ,BC = 1,所以 tan∠BSC
=
2 2.
10 把长( 正) 方体补成长( 正) 方体
图 13 图 14
例 12 如图 14,在长方体 ABCD—A1B1C1D1 中, 已知 AB = 4,AD = 3,AA1 = 2,E、F 分别是线段 AB、BC 上的点,且 EB = FB = 1,求 EC1 与 FD1 所成角的余弦 值.
=
22 5
.
图 11 图 12
例 10 在正三棱柱 ABC—A1B1C1 中, 若 AB = 2 BB1,则 AB1 与 C1B 所成角的大小为( ).
A.60° B.90° C.30° D.45°
中学数学杂志 2014 年第 11 期 ZHONGXUESHUXUEZAZHI
例 1 一个四面体的棱长都为 2 ,四个顶点都 在同一球面上,则球的表面积为( ).
A.3π B.4π C.3 3 π D.6π 解析 如图 1,把四面体补成一个棱长为 1 的 正方体,则正方体的对角线就是球的直径.因为 2R = 3 ,所以 S球表面积 = 4πR2 = 3π,故应选 A.
巧借“补形”思维,妙解立体几何问题

ʏ孙海鹰利用 补形 思维这一桥梁,可以使数学的思维方法更加活跃㊁简捷,应用起来更加灵活㊁多样,能有效培养同学们思维的灵活性㊁独创性㊂利用 补形 思维可以把空间立体几何中的一些不规则形体㊁不熟悉形体㊁残缺形体补成相应的规则形体㊁熟悉形体㊁完整形体等,对解决问题起到化繁为简㊁一目了然的作用,使得数学思维更加灵活,数学知识结构更加完整㊁充实,数学思想方法更加完美㊂一㊁还原补形法例1为了给数学家帕西奥利的‘神圣的比例“画插图,列奥纳多㊃达㊃芬奇绘制了一些多面体,图1所示的多面体就是其中之一㊂它是由一个正方体沿着各棱的中点截去八个三棱锥后剩下的部分,这个多面体的各棱长均为2,则该多面体外接球的体积为()㊂图1A.16πB.8πC.16π3D.32π3分析:对于此类空间立体几何中的不规则形体 多面体,直接处理起来有较大的难度,可借助空间几何体的还原补形法,把该多面体进行还原补形为正方体,结合补形前后对应图形中相关元素的位置关系与变化情况,进行合理分析与运算㊂解:结合图1,把该多面体进行还原补形为正方体,如图2所示㊂图2由所给多面体的棱长为2,可得正方体的棱长为22,那么正方体的中心即为多面体的外接球的球心,所以球心到多面体顶点的距离为(2)2+(2)2=2,即多面体外接球的半径R=2㊂故该多面体外接球的体积V=43πR3=32π3㊂应选D㊂还原是回归问题本质的一种逻辑推理方式㊂在解决一些空间几何体问题中,合理回归,完整地进行还原与补形是解题的关键㊂在处理空间几何体的还原补形时,要注意回归的简单几何体与 补 上去的小几何体之间要素的联系与图形之间的变化,正确构建相互之间的关系,不要出现添加或遗漏㊂二㊁联系补形法例2已知正三棱锥P-A B C,点P,A, B,C都在半径为3的球面上,若P A,P B, P C两两相互垂直,则球心到截面A B C的距离为㊂分析:此类不同空间几何体间(正三棱锥与球)的联系问题,需要进行合理补形,将正三棱锥与球这两种不同的空间几何体联系在一起,使得问题的处理直观易懂,从而便于分析与计算㊂解:由于正三棱锥的侧棱P A,P B,P C5知识结构与拓展高一数学2023年4月Copyright©博看网. All Rights Reserved.两两互相垂直,故以P A ,P B ,P C 为棱补成正方体,如图3所示㊂图3球心O 为正方体的体对角线P D 的中点,且P O =3,则正方体的棱长为2㊂设点P 到平面A B C 的距离为h ㊂根据正三棱锥的体积,借助等体积法得13ˑ34ˑ(22)2㊃h =13ˑ12ˑ2ˑ2ˑ2,解得h =233,所以所求球心到截面AB C 的距离为3-233=33㊂寻找联系是构建不同数学元素之间的桥梁㊂在空间立体几何问题中,抓住不同空间几何体之间的联系,合理补形(如三条侧棱两两互相垂直,可补形为正方体或长方体),使得问题更加直观易求㊂三㊁对称补形法 图4例3 如图4所示,在斜截圆柱中,已知圆柱的底面直径为40c m ,母线最短与最长的分别为50c m ,80c m ,则该斜截圆柱的体积V =㊂分析:此类空间几何体中的残缺形体,属于不太规则的空间几何体,直接求解无从下手,可借助空间几何体的几何特征进行合理的对称补形,将题设条件中的斜截圆柱按斜截面吻合对接,补全为一个完整的圆柱,再利用圆柱的体积公式求解㊂解:将题设条件中的斜截圆柱按斜截面吻合对接,补全为一个完整的圆柱(即斜截圆柱进行翻转对接)㊂由题意知所求体积V =12ˑ(πˑ202)ˑ(50+80)=26000π(c m 3)㊂对称是数学中的一种重要关系,也是充分展示数学美的一种表现形式㊂在解决空间几何体问题时,对于一些特殊的残缺形体,要善于发现图形中的对称关系与几何特征,借助相同图形之间的对称补形法进行化归与转化,对空间想象能力的提升很有帮助㊂编者的话: 补形 思维解决立体几何问题,是整体思想的一种具体体现,可将不规则的㊁陌生的㊁复杂的几何体补成规则的㊁熟悉的㊁简单的几何体(如常见的长方体㊁正方体㊁平行六面体㊁圆柱等),在所补成的空间几何体中研究原几何体的有关元素的位置关系㊁空间角或空间距离的计算等,从而实现问题的顺利解决㊂这类问题,能全面考查数学基础知识㊁基本技能㊁基本思想㊁基本活动经验这 四基 的落实情况,以及发现问题㊁提出问题㊁分析问题和解决问题能力的培养与提升㊂若三棱锥P -A B C 中最长的棱P A =2,且各面均为直角三角形,则此三棱锥外接球的体积是㊂图5提示:根据题意,可把该三棱锥补成长方体,如图5所示,则该三棱锥的外接球即为该长方体的外接球㊂易得外接球的半径R =12P A =1,所以该三棱锥外接球的体积V =43ˑπˑ13=43π㊂作者单位:江苏省江阴中等专业学校高新区校区(责任编辑 郭正华)6知识结构与拓展 高一数学 2023年4月Copyright ©博看网. All Rights Reserved.。
谈立体几何的补形法

谈立体几何的补形法
吴建伟
【期刊名称】《中学教研:数学版》
【年(卷),期】1992(000)001
【摘要】柱、锥、台、球等几何体,它们虽然形状不同,但在本质上存在着各种联系,在一定的条件下,可以相互转化。
通过转化,把复杂的问题归结成简单的解法,化难为易,从而得到解题的途径和方法,本文介绍立几的补形法。
检查这种方法的使用,是考查学生数学能力的一个重要方面,故在高考及各类数学竞赛中也常常出现,现举例如下: 一、补成平行六面体例1 斜三棱柱ABC—
A<sub>1</sub>B<sub>1</sub>C<sub>1</sub>的一个
【总页数】3页(P15-17)
【作者】吴建伟
【作者单位】浙江嵊县中学
【正文语种】中文
【中图分类】G633.6
【相关文献】
1.“补形法”——立体几何解题中的转化策略 [J], 简素宁
2.补形法在立体几何中的应用 [J], 陈念红
3.巧借补形法解立体几何问题 [J], 闫伟; 刘彦强
4.例谈补形法解立体几何题 [J], 刘立强;杜红全
5.例谈补形法解立体几何题 [J], 刘立强;杜红全
因版权原因,仅展示原文概要,查看原文内容请购买。
空间几何体中几种常见的补形法

s△^船 ·AA =丁1×24×8=96 .
【小结 】比较 上述 两种 方 法 ,补 形
图3
法显 然 比分割法要简 洁得 多 ,计算 量也很 小 ,但 要抓 住 图形
的对 称性 ,巧妙的补成熟悉的几何 体 ,并找到 原几何 体 与补
形后 的几何体 的关 系 ,实现化繁为 简的奇效.
了一种构造思 想 ,同时也反 映了对 立统一的辩证思想 .
利用补形 法解决立体几何 问题 的基本 步骤是 :
第一步 :把不熟悉 的或 复杂 的几 何体 延 伸或 补加 成 熟
悉的或简单 的几何 体 ,把不完整 的图形 补成完整 的图形 ;
第二 步 :运用常见几何体 的知识 等计算结果 ;
第三 步 :得 出结论.
以外接球直径 2R= ,所 以 R= ,所 以外接 球 的表 面积
s球=挚.
方 法 二 联 系补 形 例 2 已知 三棱 锥 P—ABC,PA=BC=5,朋 :AC= 4,PC:AB= l,求三棱 锥的体积. 【思路 】如按常规求法 ,需求三棱锥 的底 面积和 高 ,而高 很 难求 出.由已知三组相对棱相 等这一 特点 ,联想长 方体对 面不平行 的对 角线恰 好组 成对 棱相 等 的三棱 锥 ,因此 可把 三棱锥 P—ABC补成长方体 ,再将长方体 分割成三棱锥 P— ABC和 四个相 同体积 的三棱锥.
在高考 中 ,补形法既可 以在选 择填空 题 中体 现 ,也 可以
在解答题 中体 现 ,常见的补形法 有对称 补形 、联系补 形 和还
原补形 ,还原补形主要涉及 台体 中“还台为锥 ”.下 面结合 实
例进行剖析 :
方法一 对称补形
立体几何习题课(分割法、补形法求体积等举例)资料讲解

例6、三棱锥P-ABC中,AP=AC,PB=2,将此棱锥沿三
条侧棱剪开,其展开图是一个直角梯形P1P2P3A。 (1)求证:侧棱PB⊥ AC;
(2)求侧面PAC与底面ABC所成的角的余弦值。
P1
m
A
P
2
B
B
Ө
A
2
D
C (甲)
P2
m
m
D
C n E n P3 (乙)
解:(1)(略)
(2)甲图中,作PD⊥AC于D,连接BD,可得PDB
面的外心,即点D,∴SD⊥平面ABC。
C
∴由VS-ABC=
1 3
S△ABC•SD得三棱锥体积。
例2、在棱长为a的正方体ABCD-A1B1C1D1中, 求D1到截面C1BD的距离。
D1
A1
B1
C1
V V 提示:利用
求解。
D1C1BD = BC1D1D
D A
C B
KEY: 3 a
3
注意:等体积法求点面距离。
P
A`
P A
C A
B
P`
C B`
C` B
提示:分别以三组对棱作为一长方体的相对面的对角线,将原三棱锥补成一个长方体,如图,
则V P-ABC=V长方体-4V PABP` 。设长方体长宽高分别为a、b、c,则有:
a2b225a3 b a2 2 c c2 2 4 3 1 4 b c 5 4 V P 所A 以B 三 C 棱3 锥4 P -A5 BC4的1 6 体 积3 为4 2 05 ( 立2方0 单位)。
h V1
V2=V1+V球
R
2R
V2
小结:
1、分割法求体积; 2、利用射影面积法求二面角; 3、补形法求体积; 4、几何体展开问题。
立体几何割补法

立体几何割补法立体几何中的割补法解题技巧邹启文※ 高考提示立体几何中常用割补法解题.特别是高考中的立体几何题很多可用割补法解,有时解起来还比较容易.※ 解题钥匙例1 (2005湖南高考,理5)如图,正方体ABCD—ABCD的棱长为1,O是底面ABCD11111111的中心,则O到平面ACD的距离为( ) 112231A、 B、 C、 D、 4222分析:求点到面的距离通常是过点做面的垂线,而由于该图的局限性显然不太好做垂线,考虑O为AC的中点,故将要求的距离 11与A到面ACD的距离挂钩,从而与棱锥知识挂钩,所以可在该 111图中割出一个三棱锥A—ACD而进行解题。
111解:连AC,可得到三棱锥A—ACD,我们把这个正方体的其 1111它部分都割去就只剩下这个三棱锥,可以知道所求的距离正好为这个三棱锥的高的一半。
这个三棱锥底面为直角边为1与的直 2角三角形。
这个三棱维又可视为三棱锥C—AAC,后者高为1,底为腰是1的等腰直角三角111 2形,利用体积相等,立即可求得原三棱锥的高为,故应选B。
2例2 (2007湖南高考,理8)棱长为1的正方体ABCD—ABCD1111 的8个顶点都在球O的表面上,E,F分别是棱AA、DD的中点, 11则直线EF被球O截得的线段长为( )22A、 B、1 C、1+ D、 222分析:在该题中我们若再在正方体上加上一个球,则该图形变得复杂而烦琐,而又考虑到面AADD截得的球的截面为圆,且EF 11在截面内,故可连接球心抽出一个圆锥来。
解:如图,正方体ABCD—ABCD,依题O亦为此正方体的中心,补侧面 1111 可得圆锥0—AD(如下图), AD为平面AD,球0截平面A D1111其底面圆心正为线段AD之中点,亦为线段EF之中点,割去正方体和球 1 的其它部分,只看这个圆锥,容易看出球O截直线EF所得线段长就等于这个圆锥底面圆的直径AD之长,故选D。
1例3 (2005全国高考I,理5)如图,在多面体ABCDEF中,已知 ABCD是边长为1的正方形,且?ADE、?BCF均为正三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学:用补形法解立体几何题
1. 正四面体补为正方体
例1. 求棱长为1的正四面体的体积。
图1
分析:常规的思路是直接用三棱锥的体积公式去求,但要首先求出此三棱锥的高,求高比较繁琐。
如果将正四面体ABCD补形为正方体(如图1),那么此正方体的棱长为,因此,求正四面体的体积便有了新的求解思路:
例2. 如图2,正三棱锥S-ABC的侧棱与底面边长都相等,如果E、F、G分别是SC、AB、AC的中点,那么异面直线EF与BG所成角的余弦值等于__________。
图2
分析:常规的思路是“平移法”,取GA的中点H,连结EH、FH,则∠EFH即为所求,但解△EFH的运算量较大。
联想到正四面体可补形为正方体(如图3),相当于求与BG所成角的余弦值。
在此正方体的左边补上一个大小相同的正方体,构成一个长方体(如图4),则相当于求长方体对角线BD与侧棱所成角的余弦值。
设正方体边长为1,则长方体对角线BD的长为。
在中,
2. 三条侧棱两两垂直的三棱锥或对棱相等的三棱锥或一条侧棱垂直于底面的三棱锥都可以考虑补形为长方体
例3. 如图5,是直二面角,
,,那么AB与面β所成的角等于()
图5
A. 90°
B. 60°
C. 45°
D. 30°
分析:由α⊥β,BD⊥CD,得BD⊥α
同理得:AC⊥β
因此,AC⊥CD,BD⊥CD,AC⊥BD
不妨把三棱锥A-BCD补形为长方体(如图5),易得
∠ABC为所求的角。
在Rt△ABC中,,选D。
例4. 如图6,四面体P-ABC中,侧棱PA、PB、PC两两垂直,O为面ABC上一点,且O到平面PAB、平面PAC、平面PBC的距离分别为2,3,4,求OP的长度。
分析:可补一个“小”长方体(如图6),由此可得“小”长方体的长、宽、高分别为2,3,4,求OP长可转化为求该“小”长方体的对角线长,得:
3. 一般三棱锥(三棱柱)可补形为三棱柱(平行六面体)
例5. 已知三棱锥P-ABC中,PA⊥BC,PA=BC=a,PA、BC的公垂线段DE=h,求证三棱锥的体积是。
分析:以ABC为底面,PA为侧棱补形为一个三棱柱ABC -,进一步补形为平行六面体ABCD-(如图7),那么
由异面直线PA、BC的距离为h知:
两底面与平面的距离为h
又PA⊥BC,PA=BC=a
可求出底面的面积为,所以
例6. 已知正三棱柱ABC-,若,求与所成的角。
分析:在三棱柱ABC-的下方再补上一个大小形状一样的三棱柱-EFG,构成一个新的三棱柱ABC-EFG(如图8),连结,则∠FA1C即为所求。
易知
由知:
∠AB1G=90°
故∠FA1C=90°
4. 其它不规则几何体可视情况补形为三棱柱或平行六面体
例7. 如图9,在多面体ABCDEF中,平面ABCD是正方形,且EF∥平面ABCD。
若EF=3,且其余的棱长都是2,求该多面体的体积。
分析:先把该不规则多面体补形为三棱柱,进一步补形为平行六面体(如图9)。
可求得点F到平面的距离为。
所以
从以上几例可知,补形后的运算很简捷,难点就在于如何突破“补形”这一关。
规律是原几何体经补形后常常置身于长方体、正方体、三棱柱或平行六面体等规则几何体中,由整体再回过头来看局部,则可化难为易。
▍
▍ ▍
▍。
