1-13单导线条件平差计算--导线条件平差的定权方法
单导线加权平差1
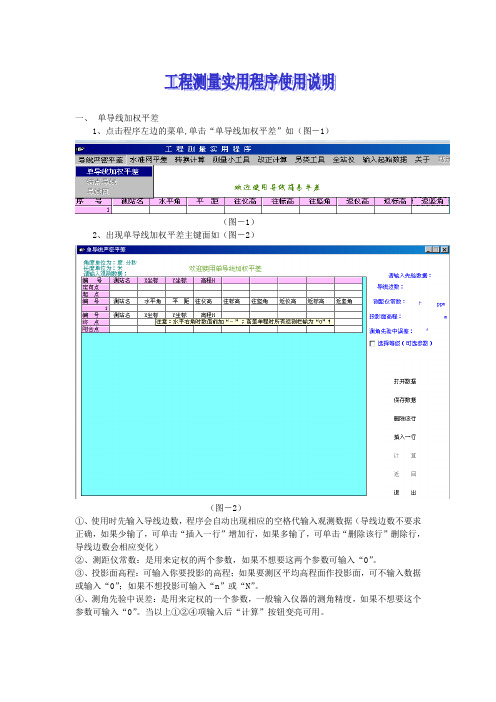
一、单导线加权平差1、点击程序左边的菜单,单击“单导线加权平差”如(图-1)(图-1)2、出现单导线加权平差主键面如(图-2)(图-2)①、使用时先输入导线边数,程序会自动出现相应的空格代输入观测数据(导线边数不要求正确,如果少输了,可单击“插入一行”增加行,如果多输了,可单击“删除该行”删除行,导线边数会相应变化)②、测距仪常数:是用来定权的两个参数,如果不想要这两个参数可输入“0”。
③、投影面高程:可输入你要投影的高程;如果要测区平均高程面作投影面,可不输入数据或输入“0”;如果不想投影可输入“n”或“N”。
④、测角先验中误差:是用来定权的一个参数,一般输入仪器的测角精度,如果不想要这个参数可输入“0”。
当以上①②④项输入后“计算”按钮变亮可用。
⑤、选择等级可选可不选,选,则平差成果表中会出现选择等级的限差,超限的提示红色;不选,则平差成果表中无限差评估。
⑥、左边表格项:定向点和附合点高程可不输,水平角输入度.分秒,如果是前进方向右角,在数据前加“-”号,程序会自动化为左角;如果高差是单向,在返向观测栏输入“0”;程序设计了检查输入错误,任何不正确的输入如:63.3.000;3-6.45;567.7+等,在按下计算按钮时,程序将提示你在某行某列输入有误。
⑦、输入完观测数据后,可点击右边的“保存数据”按钮,保存您输入的数据。
⑧、您也可以从文本中读入观测数据,点击右边的“打开”按钮,可选择您的数据文件(文本文件或DAT文件)文件格式如下:第一行:第一个数“6”为导线边数,不要求一定正确,如果不正确程序会提示,并修正此错误。
第二个数“5”为测角先验中误差;第三个数“5”为测距仪加常数;第四个数“2”为测距仪乘常数;第四个数“0”为投影面选择,“0”表示测站平均高程面,程序会计算出,“N”或“n”表示不投影,其它常数则投影面为该常数值。
第二行:为导线起点的定向点的点号,X坐标,Y坐标,高程第三行:为导线起点的点号,X坐标,Y坐标,高程第四行:为导线终点的点号,X坐标,Y坐标,高程第五行:为导线终点的定向点的点号,X坐标,Y坐标,高程以下行:为导线测站观测数据点号,水平角,平距,往测仪器高,往测标高,往测竖角,返测仪器高,返测标高,返测竖角注:⑴、起算点坐标数据,程序在读取时会格式化数据,让其只保留三位小数,程序只读取后8位数据,如2581089.5100008,程序读为“1089.510”;这样不影响导线计算,但导线点坐标成果统一差一个常数;如果要不差常数,在读入数据后,在程序的表格中把起算数据的常数加上去即可。
导线平差计算

导线平差计算1 简介闭合导线和附合导线是长输管道站场和穿跨越测量常用的控制手段,其优点是可以同时完成平面和高程控制测量。
导线平差原理请查阅相关文献。
不同平差软件的平差方法步骤基本相同,本文件基于南方平差易软件平台介绍导线(闭合导线、附合导线是最简单的导线控制网)平差的操作方法。
2 规范性引用文件下列文件中的条款通过本标准的引用而成为本标准的条款。
●《长距离输油输气管道测量规范》(SY/T 0055-2003)●《工程测量规范》(GB 50026-2007)3 操作步骤(1)录入数据录入数据是将导线测量数据录入平差软件。
可以采用手工或文件方式录入(建议采用后者,选菜单“文件/打开”)。
其数据格式如下:[NET] 控制网信息[P ARA] 控制网参数[STATION]坐标和高程信息(11表示高程已知,如果无坐标则无法在平差易中看到和输出地图)[OBSER] 观测的转角、平距、高差等信息下图为导入数据窗口:图3-1 导入数据窗口(2)坐标推算(F3)选菜单“平差/推算坐标”,根据已知条件(测站点信息和观测信息)推算出待测点的近似坐标。
为构建动态网图和导线平差作基础。
(3)概算选菜单“平差/选择概算”→配置概算参数→输出概算结果。
下图为“选择概算”的配置参数窗口:图3-2 配置概算参数(4)调整观测数据将概算结果调整到输入的观测数据中,重新导入。
(5)计算方案的选择对于同时包含了平面数据和高程数据的导线, 一般处理过程应为:先进行平面处理, 然后在高程处理时软件会使用已经较为准确的平面数据(如距离等)来处理高程数据。
对精度要求很高的平面高程混合平差,您也可以在平面和高程处理间多次切换,迭代出精确的结果(但建议平面和高程分开了平差)。
针对导线平差,需要设置中误差及仪器参数、高程平差参数、限差及等级内容。
选菜单“平差/平差方案”即可进行参数的设置,如下图:图3-3 平差方案参数设置(6)闭合差计算与检核(F2)根据观测值和设定参数来计算导线的闭合差,从而来检查某条导线是否存在观测粗差或误差。
按条件平差解算单导线和导线网
n
n
1
wy = ∑ ∆yi,i+1
i =1
n
i =2
ρ
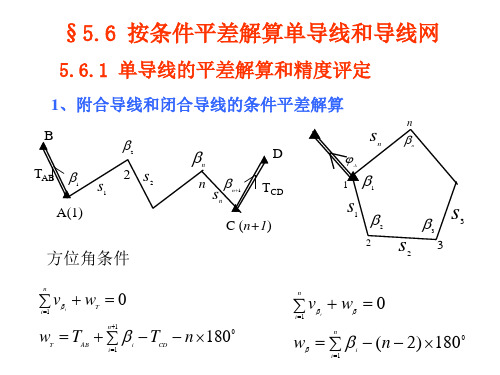
5.6.1 单导线的平差解算和精度评定
2、 无定向导线和单定向导线的平差解算 、
β
T1
2
β
s
2
n
2
s
1
n
1
Tn
sn
n+1
引入方位角条件未知数T1,Tn,采用附有未 知数的条件平差模型计算。其条件方程如下: 方位角条件:
∑ vβ + δ T − δ T + wT = 0
1
J
n
J+1
每个导线段可列出3个条件:
坐标方位角的条件式:∑ v β + δ TJ − δ TJ +1 + wT
i =1
i
nj
J , J +1
=0
其中: wT
J , J +1
= TJ + ∑ v β − TJ0+1 − n J × 180
0 i =1
i
nj
5.6.2 导线网的平差解算和精度评定
纵坐标条件式: ∑ cos Ti v s − ∑
i
ρ
1
ρ
n
wy = yA + ∑ ∆yi0,i+1 − yc
i =1
n
5.6.1 单导线的平差解算和精度评定
如果只在导线的一端引入方位角未知数 T1,则只 能列出如下两个坐标条件:
0 0 ∑ cosTi vs − ∑ ( yn+1 − yi )vβ − ( yn+1 − y1 )δ T + wx = 0 0 0 0 i =1
导线平差计算方案设置-16页文档资料

导线平差计算方案设置一、导线类型:1.闭、附合导线(图1)2.无定向导线(图2)3.支导线(图3)4.特殊导线或网(见数据输入一节),该选项适用于所有的导线,但不计算闭合差。
而且该类型不需要填写未知点数目。
当点击表格最后一行时自动添加一行,计算时删除后面的空行。
5.坐标导线。
指使用全站仪直接观测坐标、高程的闭、附合导线。
6.单面单程水准测量记录计算。
指仅进行单面读数且仅进行往测而无返测的水准测量记录计算。
当数据中没有输入“中视”时可以用作五等、等外水准等的记录计算。
当输入了“中视”时可以用作中平测量等的记录计算。
说明:除“单面单程水准测量记录计算”仅用于低等级的水准测量记录计算外,其它类型选项都可以进行平面及高程的平差计算,输入了平面数据则进行平面的平差,输入了高程数据则进行高程的平差,同时输入则同时平差。
如果不需进行平面的平差,仅计算闭、附合高程路线,可以选择类型为“无定向导线”,或者选择类型为“闭附合导线”但表格中第一行及最后一行数据(均为定向点)不必输入,因为高程路线不需定向点。
二、概算1.对方向、边长进行投影改化及边长的高程归化。
2.应选择相应的坐标系统,以及Y坐标是否包含500KM。
选择了概算时,Y坐标不应包含带号。
三、平面计算设置(一)、等级:选择等级,以便根据《工程测量规范》自动进行限差等的设置。
不同的规范,或者相同的规范但不同的版本可能技术要求不同,请在软件进行自动设置后做必要的检查,如有不符,可以自行设置。
(二)、近似平差与严密平差的选择及近似平差的方位角、边长是否反算1.近似平差:程序先分配角度闭合差再分配坐标增量闭合差,即分别平差法。
2.严密平差:按最小二乘法原理平差。
3.《工程测量规范》规定:一级及以上平面控制网的计算,应采用严密平差法,二级及以下平面控制网,可根据需要采用严密或简化方法平差。
当采用简化方法平差时,应以平差后坐标反算的角度和边长作为成果。
《城市测量规范》规定:四等以下平面控制网可采用近似平差法和按近似方法评定其精度。
单一闭合导线近似平差的步骤与公式培训讲学

写出单一闭合导线近似平差的步骤与公式,指出附合导线和闭合导线计算中的不同点。
1. 检查并整理外业观测成果;
2. 计算角度闭合差并调整,∑⨯--=180)2(n f ββ
,当满足限差要求后可调整,n f v i /β
β-=,检核:ββf v i -=∑; 3.
4. 坐标方位角推算:180±+=左后前βαα或180±-=右后前βαα,检核已知
边方位角;
5. 坐标增量计算:ij ij ij
s x αcos ⨯=∆,ij ij ij s y αsin ⨯=∆; 6.
7. 坐标增量闭合差的计算与调整:
∑∆=x f x ,∑∆=y f y ,∑+=s f f k y x /22,当满足要求时可调整,∑⨯-=∆s s f v ij x xij /,∑⨯-=∆s s f v ij y yij /,检核:x xij f v -=∑∆,y yij f v -=∑∆;
8.
9.
10.
11. 待定点坐标计算:1,1,1+∆+++∆+=i i x i i i i v x x x ,1
,1,1+∆+++∆+=i i y i i i i v y y y ,检核:计算回已知点。
附和导线与闭合导线计算中的不同点在于:
1.
2.
3.
4.角度闭合差的计算;坐标增量闭合差的计算。
导线平差_精品文档

导线平差导线平差是指在测量或建设中进行的一项重要的技术工作,主要是为了保证导线的水平和垂直度,确保测量结果的准确性和可靠性。
在工程测量中,导线平差是不可或缺的一环,它可以帮助测量人员更好地掌握实地的情况,从而更准确地进行导线的布设和定位。
导线平差的原理是根据测量数据进行误差分析和修正,通过一系列的计算和调整,可以得到最为精确的导线位置和方向。
具体来说,导线平差包括两个方面的工作:平差计算和平差调整。
平差计算是根据测量数据,结合误差理论和数学方法,计算出导线的真实位置和方向;平差调整是通过人工或仪器,对导线进行微调,以保证导线的准确性。
在导线平差中,最常用的计算方法是最小二乘法。
最小二乘法是一种通过最小化测量数据与理论模型之间的偏差,来求解未知量的一种数学方法。
在导线平差中,我们可以将导线的真实位置和方向作为未知量,通过最小二乘法求解出来。
最小二乘法的基本原理是将导线的测量数据表示为一组方程组,其中未知量为导线的位置坐标和方向角。
通过最小二乘法,可以求解出最优解,使得测量数据与理论模型之间的偏差最小。
在计算过程中,需要考虑测量误差和观测精度对最终结果的影响。
除了最小二乘法,导线平差还可以采用其他的计算方法,如加权平差法和GPS平差法等。
这些方法在实际应用中,可以根据具体情况选择合适的方法。
导线平差的调整工作是为了进一步提高导线的准确性和可靠性。
在平差调整中,可以采用各种手段,如利用导线标杆进行修正、使用仪器进行微调等。
通过这些调整工作,可以使导线的位置和方向更加准确,从而提高测量结果的质量。
导线平差在工程测量中具有重要的应用价值。
首先,导线平差可以减小测量误差,提高测量精度。
导线平差可以根据实地情况进行修正,避免由于环境和操作因素引起的误差。
其次,导线平差可以提高导线的可靠性和稳定性。
通过导线平差的调整工作,可以使导线的位置和方向更加准确,从而保证测量结果的可靠性。
最后,导线平差可以为后续的工作提供基础。
条件平差的基本原理

v1
V
n ,1
v2
vn
wa F1L1, L2 ,, Ln
wb F2 L1, L2 ,, Ln
wr Fr L1, L2 ,, Ln
则相应方程的矩阵表达式分别为
F Lˆ 0
AV W 0 W FL
3. 基础方程
按求函数极值的拉格朗日乘数法,设乘数
5)求观测值的平差值; Lˆ L V
6)检核。 F (Lˆ) 0
7)检核。
3. 实例分析 例6-1水准网如右图:观测值及其权矩阵如下:
L 0.023 1.114 1.142 0.078 0.099 1.216 T m
P diag1 1 1 2.5 2.5 2.5
求各水准路线的最或然值。
解: 1)列出条件方程
或
v1 v2 v3 v2
0 0 v4 4 0
v1
1 0
1 1
1 0
0 1
v2 vv43
0 4
0 0
令c=1,则由定权公式
,有 pi
C Si
1 Si
P 1
1 p1
0
0
0
0
1 p2
0
0
0
0
1 p3
0
0 s1 0 0 0 2 0 0 0
0 0
0 0
1 p4
0
K
r ,1
ka
kb
kr T
,称为联系数向量。组成函数
V T PV 2K T AV W
将 φ 对V 求一阶导数,并令其为零,得
d dV
2V T P
2KT
A
0
两边转置,得
第三章条件平差
独立三角网
自由三角网
自由测角网
附合三角网(测角)
• 例:
∆ቤተ መጻሕፍቲ ባይዱ
α ∆
当n=35、n=22、n=35+22时,其条件式个数各为多 少?有哪些类型?
图形条件(内角和条件):
B
b1
a2
c1 D c2 a1 b3 c3 a3 b2 C
A
圆周条件(水平条件):
b1
a2
c1 a1 a3 c3
c2 b2 b3
5.1.06、 5.1.07
上节内容回顾:
改正数条件式 观测值的协方差阵 法方程
AV W 0
D P Q
2 0 1 2 0
r n n n
Naa K W 0 N aa AQ AT
r r n r
改正数方程
V P A K QA K
T
1 T
wr
T
• 则条件方程可写成:
ˆA 0 AL 0
• 以及改正数条件式:
W AL A0
AV W 0
这样一来,对于一个平差问题,我们能够得到 其数学模型:
AV W 0 D P Q
2 0 1 2 0
下面要解决的问题是: 由上述的数学模型来求改正数V。
不难发现,不能求得V的唯一解!!! 解决不唯一解的办法就是附加一个约束条件---“最小二乘估计” 即满足:
极条件(边长条件):
b1 a2
c1
a1 b3 c3
c2 b2 a3
极条件(边长条件)就是指由不同路线推算得到 的同一边长的长度应相等。
三角网的基本图形 1) 单三角形 2)大地四边形
3)中点多边形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
B(1)
附合导线示例图
C(N+1)
导线条件平差的定权方法
图示为一四等附合导线,《规范》 A 测角中误差 2.5,测边所用测距 仪的标称精度公式 S 5mm 5 ppmDkm 。 已知数据和观测值见表1、表2。
试确定观测值的权阵。
β2
2
β3
β1 S1
S2 3
B(1)
附合导线示例图
Xi’an University of Science & Technology
举一 反三
治学 严谨
Error Theory and Surveying Adjustment
逻辑
性强
主讲人:史经俭 张静 席晶
本讲内容
导线条件平差的定权方法
分析
任务
1:求出观测值的平差值, 未知点坐标平差值;
2:进行精度评定。
P 0
0
4.3 0 0 3.3
0 0
0 0
0 0
0 0
0 0
0 0
观 测
0 0
0 0
2.8 0
0 1
0 0
0 0
0 0
0 0
值 独 立
0 0 0 0 1 0 0 0 为
0
0
0 0
0 0
0 0
0 0
0 0
1 0
0 1
0 0
对 角
0
0
0
0 0 0 0 0 1 阵
β5 D
表2
起算数据表
点号
B C
纵坐标x(m) 横坐标y(m)
187396.252 29505530.009 184817.605 29509341.482
方位角T
TAB = 161˚44′07.2″ TCD = 249˚30′27.9″
导线条件平差的定权方法
单位权中误差
0 2.5"
A
角度观测值的权
p 1
第一条边的测边中误差
S 1 5mm 5mm 1.474444 12.4mm
根据提供的标称精度公式 S 5mm 5 ppmDkm
β2
2
β3
β1 S1
S2 3
B(1)
附合导线示例图
β4 S3 4
S4
C(5)
第一条边的权值
pS 1
2 0
2 S1
0 0 0 0 0 0 1 0 0
4. 权 0是相0 对0精度0 0 0 0 1 0
0 0 0 0 0 0 0 0 1
理论
感谢聆听,批评指导
公式
思考
平差
算例
导线边长观测值(m)
设观测值向量为: L S1 S2 S3 S4 1 2 3 4 5 T
S1 = 1474.444 S3 = 1749.322 S2 = 1424.717 S4 = 1950.412
,
观测值的权阵、权逆阵
4.1 0 0 0 0 0 0 0 0
0
0
0
]1N
wy
0
A
D
β2
β4
βN
2
4
S1 β1
S2 β3 S3
N
SN-1
SN βN+1
3
B(1)
附合导线示例图
C(N+1)
导线条件平差的定权方法
权的定义
设有观测值 Li i 1,2,,n,它们的方
差为
2 i
,选定任一常数
0
,定义观测值
Li
的权为:
pi
2 0
2 i
权3.的特0 点的不可变性
随机模型
D
n,n
2 0
Q
n,n
2 0
P 1
n,n
导线条件平差的定权方法
导线条件平差的函数模型
AV W 0 [vi
]n1
1
wT
0
[cos Ti
vSi
]1N
1
[( yN 1
yi )vi
]1N
wx
0
[sin Ti
vSi
]1N
1
[(xN1xi )vi2.52 1.242
4.1
(秒2/厘米2)
注:在计算边长的权时根据具体情况取(秒2/厘米2)、 (秒2/毫米2)等。
β5 D
导线边长观测值(m) S1 = 1474.444 S3 = 1749.322 S2 = 1424.717 S4 = 1950.412
导线条件平差的定权方法
同理得: pS 1 4.1,pS 2 4.3,pS 3 3.3,pS 4 2.8。
1. 权大的观测值的精度高
为了使权能起到比较精
2. 权的大小可变,但比值不变
度高低的作用,在同一问题中
3. 0 的不可变性
只能选定一个 4. 权是相对精度
0
值。
两类观测值:
角度N+1个,边长N个。
? 如何选 0 ,如何定权呢
A
D
β2
β4
βN
2
4
S1 β1
S2 β3 S3
N
SN-1
SN βN+1
权 4的10.1 特10点
0 0
0 0 0 0 0 0
0 0 0 0 0 0
4.3
1. 权 0大的0 观31测.3 值0 的0精0度0高0 0 2P.1 权 0的大0 小0可变21.8,0但0比0值0不0变
0 0 0 0 1 0 0 0 0
3. 00的不0 可0变性0 0 1 0 0 0
β4 S3 4
S4
C(5)
表1
观测值数据表
导线边长 观测值(m)
S1 = 1474.444 S2 = 1424.717 S3 = 1749.322 S4 = 1950.412
转折角度观测值
β1 = 85˚30′ 21.1″ β2 = 254˚32′ 32.2″ β3 = 131˚04′ 33.3″ β4 = 272˚20′ 20.2″ β5 = 244˚18′ 30.0
