(新)角平分线与垂直平分线练习题(经典)
圆形角平分线与垂直平分线练习题(经典)

圆形角平分线与垂直平分线练习题(经典)题目一在一个半径为 $r$ 的圆内,作一条角平分线,连接圆心和角平分线的交点,记为 $A$。
请证明:线段 $AO$ 垂直于角所对的弧。
题目二在一个半径为 $r$ 的圆内,作一条垂直平分线,连接圆心和垂直平分线的交点,记为 $B$。
设角 $BOC$ 为 $\alpha$ 度,请求弧$BC$ 所对的角大小。
题目三在一个半径为 $r$ 的圆内,作一条垂直平分线,连接圆心和垂直平分线的交点,记为 $D$。
设垂直平分线与弧 $AB$ 的交点分别为 $E$ 和 $F$。
请证明:角 $DEF$ 为直角。
题目四在一个半径为 $r$ 的圆内,作一条垂直平分线,连接圆心和垂直平分线的交点,记为 $G$。
设角 $DGH$ 为 $\beta$ 度,角$GHJ$ 为 $\gamma$ 度,求证:$\beta$ 度和 $\gamma$ 度的和等于$90$ 度。
解答题目一首先,考虑将圆分成 $4$ 个相等的扇形,由于扇形的圆心角相等,每个扇形的圆心角为 $90$ 度。
现在我们将扇形 $AOB$ 的边$OA$ 延长,交于圆上的点 $C$,如下图所示:A/// C/B根据圆心角的性质,可以知道圆心角 $ACB$ 等于扇形角$AOB$,即 $ACB=90$ 度。
又因为 $\angle OAC$ 是角 $OAB$ 的角平分线,所以 $\angle OAC = \angle CAB = \angle CBA = \frac{1}{2} ACB = 45$ 度。
现在我们要证明 $AO$ 垂直于弧 $AB$。
设 $AD$ 是半径 $r$,由于角 $OAD$ 是 $45$ 度,根据直角三角形的性质,我们可以得到:\[\sin 45^\circ = \frac{AD}{AO}\]而正弦 $45$ 度是 $\frac{1}{\sqrt{2}}$,所以我们得到 $AD =\frac{AO}{\sqrt{2}}$。
2023年暑假新八年级数学预习专题5:角平分线与垂直平分线(精练教师版)
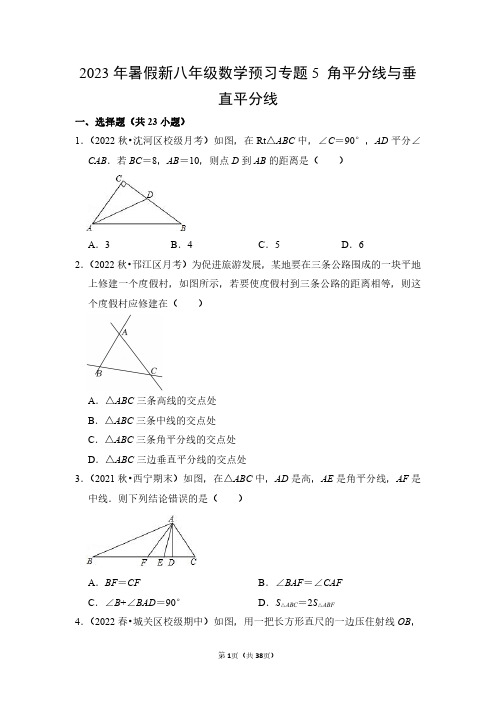
AD 过点 P 且与 AB 垂直.若 AD=8,BC=10,则△BCP 的面积为( )
第 2页(共 38页)
A.16
B.20
C.40
D.80
8.(2022•鼓楼区校级开学)三条公路围成一个三角形区域,某地区决定在这个
三角形区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,则
这个集贸市场应建在( )
D.有无数处
16.(2022 春•港北区期末)如图,已知△ABC 的周长是 36cm,∠ABC 和∠ACB
的角平分线交于点 O,OD⊥BC 于点 D,若 OD=3cm,则△ABC 的面积是( )
A.48cm2
B.54cm2
C.60cm2
D.66cm2
17.(2022 春•任城区期末)如图,在△ABC 中,∠ABC 的角平分线和∠ACB 相
的数量关系,下列说法正确的是( )
A.S1=4S2
B.S1=3S2
C.S1=2S2
D.S1=S2
15.(2022 春•兰州期末)某镇要在三条公路围成的一块三角形平地内修建一个
第 4页(共 38页)
砂石场,如图,要使这个砂石场到三条公路的距离相等,则可供选择的地址 ()
A.仅有一处 B.有四处
C.有七处
上修建一个度假村,如图所示,若要使度假村到三条公路的距离相等,则这
个度假村应修建在( )
A.△ABC 三条高线的交点处 B.△ABC 三条中线的交点处 C.△ABC 三条角平分线的交点处 D.△ABC 三边垂直平分线的交点处 3.(2021 秋•西宁期末)如图,在△ABC 中,AD 是高,AE 是角平分线,AF 是 中线.则下列结论错误的是( )
AE 是角平分线,AF 是中线,则下列说法中错误的是( )
垂直平分线和角平分线典型题

知识要点详解1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示:如图1,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若点C 在直线m 上,则AC =BC.定理的作用:证明两条线段相等 (2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示:如图2,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若AC =BC ,则点C 在直线m 上.定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线,,i j k 分别是△ABC 三边AB 、BC 、CA 的垂直平分线,则直线,,i j k 相交于一点O ,且OA =OB =OC.定理的作用:证明三角形内的线段相等.(2)三角形三边垂直平分线的交点位置与三角形形状的关系:若三角形是锐角三角形,则它三边垂直平分线的交点在三角形内部;若三角形是直角三角形,则它三边垂直平分线的交点是其斜边的中点;若三角形是钝角三角形,则它三边垂直平分线的交点在三角形外部.反之,三角形三边垂直平分线的交点在三角形内部,则该三角形是锐角三角形;三角形三边垂直平分线的交点在三角形的边上,则该三角形是直角三角形;三角形三边垂直平分线的交点在三角形外部,则该三角形是钝角三角形.图1图2经典例题:例1 如图1,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC 的长等于( )A .6cmB .8cmC .10cmD .12cm课堂笔记:针对性练习::1)如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点 E ,如果△EBC 的周长是24cm ,那么BC= 2) 如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点E ,如果BC=8cm ,那么△EBC 的周长是3) 如图,AB=AC,AB 的垂直平分线交AB 于点D ,交AC 于点E ,如果∠A=28 度,那么∠EBC 是例2. 已知: AB=AC ,DB=DC ,E 是AD 上一点,求证:BE=CE 。
线段垂直平分线与角平分线练习题

线段的垂直平分线与角的平分线一、选择题1.如图1,在△ABC 中,AD 平分∠CAE ,∠B=30︒,∠CAD=65︒,那么∠ACD 等于 ( )A .50︒B .65︒C .80︒D .95︒2.如图2,在△ABD 中,AD=4,AB=3,AC 平分∠BAD ,那么:ABC ACD S S ∆∆= ( )A .3:4B .4:3C .16:19D .不能确信3.如图3,在△ABC 中,∠C=90︒,AD 平分∠BAC ,DE ⊥AB 于E ,那么以下结论:①AD 平分∠CDE ; ②∠BAC=∠BDE ;③DE 平分∠ADB ;④BE+AC=AB 。
其中正确的有 ( ) A .2个 B .3个 C .4个 D .1个4.如图4,AD ∥BC ,∠D=90︒,AP 平分∠DAB ,PB 平分∠ABC ,点P 恰好在CD 上,那么PD 与PC的大小关系是 ( )A .PD>PCB .PD<PC C .PD=PCD .无法判定 。
五、在三角形内部,有一点P 到三角形三个极点的距离相等,那么点P 必然是( )A 、三角形三条角平分线的交点;B 、三角形三条垂直平分线的交点;C 、三角形三条中线的交点;D 、三角形三条高的交点。
六、已知△ABC 的三边的垂直平分线交点在△ABC 的边上,那么△ABC 的形状为( )A 、锐角三角形;B 、直角三角形;C 、钝角三角形;D 、不能确信7、如下图,在△ABC 中,∠BAC =90°,AD ⊥BC 于D ,BE 平分∠ABC 交AD 于E ,F 在BC 上,而且BF =AB ,那么以下四个结论:①EF ∥AC ,②∠EFB =∠BAD ,③AE =EF ,④△ABE ≌△FBE ,其中正确的结论有 ( )A 、①②③④B 、①③C 、②④D 、②③④PD CBAEDCB A DCB AE D CBA图3 图4图1图27题图 8题图 9题图八、如下图,在ABC ∆中,∠C =90°, AC =4㎝,AB =7㎝,AD 平分∠BAC 交BC 于D ,DE⊥AB ,那么EB 的长是 ( )A 、3㎝B 、4㎝C 、5㎝D 、不能确信九、随着人们生活水平的不断提高,汽车慢慢进入到千家万户,小红的爸爸想在本镇的三条彼此交叉的公路(如下图),建一个加油站,要求它到三条公路的距离相等,如此可供选择的地址有( )处。
线段垂直平分线与角平分线练习题

线段垂直平分线与角平分线练习题线段的垂直平分线和角的平分线是三角形中常见的概念。
下面是一些与此相关的选择题。
1.在三角形ABC中,AD平分∠CAE,∠B=30°,∠CAD=65°,则∠ACD等于()A。
50° B。
65° C。
80° D。
95°2.在三角形ABD中,AD=4,AB=3,AC平分∠BAD,则S△A。
3:4 B。
4:3 C。
16:19 D。
不能确定3.在三角形ABC中,∠C=90°,AD平分∠BAC,DE⊥XXX于E,则下列结论正确的有()A。
2个 B。
3个 C。
4个 D。
1个4.在四边形ABCD中,AD∥BC,∠D=90°,AP平分∠DAB,PB平分∠ABC,点P恰好在CD上,则PD与PC的大小关系是()A。
PD>PC B。
PD<PC C。
PD=PC D。
无法判断除了选择题,还有以下问题:5.在三角形内部,有一点P到三角形三个顶点的距离相等,则点P一定是什么?6.已知△ABC的三边的垂直平分线交点在△ABC的边上,则△ABC的形状是什么?7.在三角形ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于E,F在BC上,并且BF=AB,则下列四个结论正确的有()A。
①②③④ B。
①③ C。
②④ D。
②③④8.在直角三角形ABC中,AC=4㎝,AB=7㎝,AD平分∠BAC交BC于D,DE⊥AB,则EB的长度是多少?A。
3㎝ B。
4㎝ C。
5㎝ D。
不能确定9.XXX的爸爸想在本镇的三条相互交叉的公路建一个加油站,要求它到三条公路的距离相等,可供选择的地址有几个?A。
1 B。
2 C。
3 D。
410.到三角形三条边的距离都相等的点是这个三角形的什么?A。
三条中线的交点 B。
三条高的交点线段的垂直平分线和角的平分线是三角形中常见的概念。
以下是与此相关的选择题和问题。
1.在三角形ABC中,AD平分∠CAE,∠B=30°,∠CAD=65°,求∠ACD的度数。
垂直平分线与角平分线(习题及答案).

垂直平分线与角平分线(习题)➢复习巩固1.到三角形三条边的距离都相等的点是这个三角形的()A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点2.如图,在△ABC 中,AF 平分∠BAC,AC 的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C 的度数为.第2 题图第3 题图3.如图,AD 是∠BAC 的平分线,DE⊥AB 于点E,若S△ABC=6,AB=4,AC=3,则线段DE 的长为.4.如图,P 是∠AOB 平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D,连接CD.求证:OP 是CD 的垂直平分线.5.如图,点P 为锐角∠ABC 内一点,点M 在边BA 上,点N 在边BC 上,且PM=PN,∠BMP+∠BNP=180°.求证:BP 平分∠ABC.16.如图,点D 在边AC 上,∠ABD+∠ABC =180°,CE 平分∠ACB 交AB 于点E,连接DE.求证:DE 平分∠ADB.7.如图,在△ABC 中,AB=AC,小聪同学利用直尺和圆规完成了如下操作:①作∠BAC 的平分线AM 交BC 于点D;②作边AB 的垂直平分线EF,EF 与AM 相交于点P;③连接PB,PC.若∠ABC=70°,则∠BPC 的度数为.8.如图,已知△ABC(AC<BC),求作:(不写作法,保留作图痕迹)(1)BC 边上的高;(2)在BC 上确定一点P,使PA+PC=BC.9.如图,已知线段a,利用尺规求作以a 为底、以2a 为高的等腰三角形.(不写作法,保留作图痕迹)10.如图,有三幢公寓楼分别建在点A,点B,点C 处,AB,AC,BC 是连接三幢公寓楼的三条道路,要修建一超市P,按照设计要求,超市要在△ABC 的内部,且到A,C 的距离必须相等,到两条道路AC,AB 的距离也必须相等,请利用尺规作图确定超市P 的位置.(不写作法,保留作图痕迹)【参考答案】➢复习巩固1. D2. 24°3. 12 74.证明略;提示:先证Rt△POC≌Rt△POD(HL),得到OC=OD,由“到一条线段两个端点距离相等的点,在这条线段的垂直平分线上”求证5.证明略;提示:过点P 分别作PD⊥AB 于D,PE⊥BC 于E,先证△PMD≌△PNE(AAS),得到PD=PE,再由“在一个角的内部,到角的两边距离相等的点在这个角的平分线上”求证6.证明略;提示:过点E 分别作EF⊥AC 于F,EH⊥BD 于H,EG⊥BC 于G,证EF=EG=EH,求证7. 80°8.作图略提示:(1)过直线外一点作已知直线的垂线;(2)作线段AB 的垂直平分线9.作图略10.作图略提示:作线段AC 的垂直平分线和∠CAB 的角平分线;。
垂直平分线与角平分线典型题练习题

线段的垂直平分线与角平分线〔1〕经典例题:例1 如图1,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,那么AC 的长等于〔 〕 A .6cm B .8cmC .10cmD .12cm针对性练习::1)如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点 E ,若是△EBC 的周长是24cm ,那么BC= 2) 如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点E ,若是BC=8cm ,那么△EBC 的周长是3) 如图,AB=AC,AB 的垂直平分线交AB 于点D ,交AC 于点E ,若是∠A=28 度,那么∠EBC 是例2. : AB=AC ,DB=DC ,E 是AD 上一点,求证:BE=CE 。
针对性练习::在△ABC 中,ON 是AB 的垂直平分线,OA=OC,求证:点O 在BC 的垂直平分线.例3. 在△ABC 中,AB=AC ,AB 的垂直平分线与边AC 所在的直线相交所成锐角为50°,△ABC 的底角∠B 的大小为_______________。
针对性练习:1. 在△ABC 中,AB=AC ,AB 的垂直平分线与AC 所在直线相交所得的锐角为40°,那么底角B 的大小为________________。
例4、如图8,AD 是△ABC 的BC 边上的高,且∠C =2∠B ,求证:BD =AC +CD.O B A C NB课堂练习:1.如图,AC =AD ,BC =BD ,那么〔 〕 垂直平分AD 垂直平分CD 平分∠ACB2.若是三角形三条边的中垂线的交点在三角形的外部, 那么,那个三角形是〔 〕3.以下命题中正确的命题有〔 〕①线段垂直平分线上任一点到线段两头距离相等;②线段上任一点到垂直平分线两头距离相等;③通过线段中点的直线只有一条;④点P 在线段AB 外且PA =PB ,过P 作直线MN ,那么MN 是线段AB 的垂直平分线;⑤过线段上任一点能够作这条线段的中垂线. 个 个 个 个4.△ABC 中,AB 的垂直平分线交AC 于D ,若是AC =5 cm ,BC =4cm ,那么△DBC 的周长是〔 〕 A.6 cm B.7 cm C.8 cm D.9 cm5.如图,在△ABC 中,AB =AC ,O 是△ABC 内一点,且OB =OC ,求证:AO ⊥B C.6.如图,在△ABC 中,AB =AC ,∠A =120°,AB 的垂直平分线MN 别离交BC 、AB 于点M 、N . 求证:CM =2BM .课后作业:1. 如图7,在△ABC 中,AC =23,AB 的垂直平分线交AB 于点D ,交BC 于点E ,△ACE 的周长为50,求BC 边的长.2. :如以下图,∠ACB ,∠ADB 都是直角,且AC=AD ,P 是AB 上任意一点,求证:CP=DP 。
线段的垂直平分线、角平分线经典习题及答案#精选、

3.线段的垂直平分线4.角平分线例1:(1)在△ABC 中,AB =AC ,AB 的垂直平分线交AB 于N ,交BC 的延长线于M ,∠A =040,求∠NMB 的大小(2)如果将(1)中∠A 的度数改为070,其余条件不变,再求∠NMB 的大小(3)你发现有什么样的规律性?试证明之.(4)将(1)中的∠A 改为钝角,对这个问题规律性的认识是否需要加以修改例2:在△ABC 中,AB 的中垂线DE 交AC 于F ,垂足为D ,若AC=6,BC=4,求△BCF 的周长。
例3:如图所示,AC=AD ,BC=BD ,AB 与CD 相交于点E 。
求证:直线AB 是线段CD 的垂直平分线。
AC DEBA B C NM AB C N M AB CN M例4:如图所示,在△ABC中,AB=AC,∠BAC=1200,D、F分别为AB、AC的中点,,,E、G在BC上,BC=15cm,求EG的长度。
⊥⊥DE AB FG ACAB E G C例5::如图所示,Rt△ABC中,,D是AB上一点,BD=BC,过D作AB的垂线交AC于点E,CD交BE于点F。
求证:BE垂直平分CD。
CEFA D B例6::在⊿ABC中,点O是AC边上一动点,过点O作直线M N∥BC,与F,求证:OE=OF例7、如图所示,AB>AC,∠A的平分线与BC的垂直平分线相交于D,自D作DE AB⊥于,求证:BE=CF。
E,DF AC FAEB M CFD答案如下:例1:解:(1)∵∠B= 1/2(180°-∠A)=70°,∴∠M=20°;(2)同理得,∠M=35°;(3)规律是:∠M的大小为∠A大小的一半,即:AB的垂直平分线与底边BC 所夹的锐角等于∠A的一半.证明:设∠A=α,则有∠B= 1/2(180°-α),∠M=90°- 1/2(180°-α)= 1/2α.(4)改为钝角后规律成立.上述规律为:等腰三角形一腰的垂直平分线与底边相交所成的锐角等于顶角的一半.例2:解:连接BF,由线段的垂直平分线的性质可得,FB=FA又因为AC=AF+CF =6,所以BF+CF=6△BCF的周长=BC+CF+BF=4+6=10例3:证明:因为AC=AD所以A在线段CD的垂直平分线上又因为BC=BD所以B在线段CD的垂直平分线上所以直线AB是线段CD的垂直平分线例4:解:作AH⊥BC于H,HC=15/2∵等腰∴∠ACB=∠ABC=30°∴AC=2EC/根号3EC=5根号3∵F为AC中点∴FC=5/2根号3∵FG⊥AC∴CG=5同理,BE=5∴EG=5例5:证明:∵DE⊥AB,∠ACB=90∴∠BDE=∠ACB=90∵BD=BC,BE=BE∴△BCE≌△BDE (HL)∴∠CBE=∠DBE∵BF=BF∴△BCF≌△BDF (SAS)∴∠BFC=∠BFD,CF=DF∵∠BFC+∠BFD=180∴∠BFC=∠BFD=90∴BE⊥CD∴BE垂直平分CD例6:解:∵MN∥BC,∴∠OEC=∠BCE,∠OFC=∠GCF,又已知CE平分∠BCO,CF平分∠GCO,∴∠OCE=∠BCE,∠OCF═∠GCF,∴∠OCE=∠OEC,∠OCF=∠OFC,∴EO=CO,FO=CO,∴EO=FO.例7:证明:连接DC,DB∵点D在BC的垂直平分线上∴DB=DC∵D在∠BAC的平分线上∴DE=DF∵∠DFC=∠DEB∴△DCF≌△DEB∴CF=BE最新文件仅供参考已改成word文本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0角平分线
角平分线性质定理:角平分线上的点到这个角两边的距离相等。
角平分线的判定: 到一个叫两边的距离相等的点在这个角的平分线上。
例1.如图,在ABC △中,90C ∠=,AD 平分CAB ∠,8cm 5cm BC BD ==,,那么D 点
到直线AB 的距离是 cm .
例2.如图,已知在Rt △ABC 中,∠C =90°, BD 平分∠ABC , 交AC 于D .
(1) 若∠BAC =30°, 则AD 与BD 之间有何数量关系,说明你的理由; (2) 若AP 平分∠BAC ,交BD 于P , 求∠BPA 的度数.
3、考点深入练习
例3:如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG 。
求证:(1)AD=AG ,(2)AD 与AG 的位置关系如何。
例4:两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B ,C ,E 在同一条直线上,连结DC .(8分)
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母); (2)证明:DC ⊥BE
B
P
A
B
C
D G
H
F
E D
C
B
A
例5:△DAC, △EBC 均是等边三角形,AE,BD 分别与CD,CE 交于点M,N. 求证:(1)AE=BD (2)CM=CN (3) △CMN 为等边三角形(4)MN ∥BC
垂直平分线的性质与判定强化练习
1如图1,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC 的长等于 ( ) A .6cm B .8cm C .10cm D .12cm
2题
2如图,在Rt ABC △中,90ACB D E ∠=,,分别为AC AB ,的中点,连DE CE ,. 下列结论中不一定正确的是 ( ) A .ED BC ∥ B .ED AC ⊥ C .ACE BCE ∠=∠
D .A
E CE =
3、△ABC 中,∠C=90°,AB 的中垂线交直线BC 于D ,若∠BAD -∠DAC=22.5°,则∠B 等于 ( ) A.37.5° B.67.5° C.37.5°或67.5° D.无法确定
4、线段的垂直平分线上的点_____________________________________.
5、到一条线段的两个端点的距离相等的点,______________________.
6、如图,在△ABC 中,AC 的垂直平分线交AC 于E ,交BC 于D ,△ABD 的周长是12 cm ,AC=5cm ,则
AB+BD+AD= cm ;AB+BD+DC= cm
;△ABC
的周长是 cm 。
3题 4题
7、如图,在Rt △ABC 中,∠C=90°,∠B=15°,DE 是AB 的中垂线,垂足为D ,交BC 于E ,BE=5,则AE=__________,∠AEC=__________,AC=__________ 。
D A C
B N M
E
8在△ABC 中,∠C =90°,用直尺和圆规在AC 上作点P ,使P 到A 、B 的距离相等(保留作图痕迹,不写作法和证明).
9如图4,AB=AD ,BC=CD ,AC 、BD 相交于点E .由这些条件可以得出若干结论,请你写出其中三个正确结论(不要添加字母和辅助线,不要求证明).
10、如右图,在△ABC 中,AB=AC , BC=12,∠BAC =120°,AB 的垂直平分线交BC 边于点E , AC 的垂直平分线交BC 边于点N 。
(1) 求△AEN 的周长。
(2) 求∠EAN 的度数。
(3) 判断△AEN 的形状。
11、如图,已知线段CD 垂直平分线AB ,AB 平分CAD ∠问AD 与BC 平行吗?请说明理由。
12、如图,已知AOB ∠和AOB ∠内两点M 、N 画一点P 使它到AOB ∠的两边距离相等,且到点M 和N 的距离相等。
A
B
C
D
E M
N
如图,在△ABC的AB、AC边的外侧作等边△ACE和等边△ABF,连接BE、CF相交于
点O,
(1)求证:CF=BE;
(2)连AO,则:①AO平分∠BAC;②OA平分∠EOF,你认为正确的是
②
(填①或②).并证明你的结论.
(1)证明:∵△ABF和△ACE是等边三角形,
∴AB=AF,AC=AE,∠FAB=∠EAC=60°,
∴∠FAB+∠BAC=∠EAC+∠BAC,
即∠FAC=∠BAE,
在△ABE与△AFC中,
AB=AF ∠BAE=FAC AE=AC
∴△ABE≌△AFC(SAS)∴BE=FC;
(2)解:连AO,过A分别作AP⊥CF与P,AM⊥BE于Q,如图,
∵△ABE≌△AFC,
∴S△A B E=S△A F C,
∴
1
2
AP•CF=
1
2
AQ•BE,
而CF=BE,
∴AP=AQ,
∴OA不一定平分∠MAN,所以①错误;
∵在RT△AOP和RT△AOM中,
AP=AM
AO=AO
,
∴RT△AOP≌RT△AOM(HL)
∴∠AOF=∠AOE,所以②正确.故答案为②.。
