高数空间几何向量典型例题

合集下载

高等数学向量代数与空间解析几何题【精选文档】

第五章向量代数与空间解析几何5。

1。

1 向量的概念例1 在平行四边形中，设＝a，＝b.试用a和b表示向量、、和,这里是平行四边形对角线的交点（图5－8）解由于平行四边形的对角线互相平行，所以a＋b＝＝2即－(a＋b）＝2于是＝（a＋b)。

因为＝－，所以（a＋b）。

图5－8又因－a＋b＝＝2，所以＝（b－a）.由于＝－，＝（a－b）.例2 设液体流过平面S上面积为A的一个区域,液体在这区域上各点处的速度均为（常向量）v.设n为垂直于S的单位向量(图5－11（a)）,计算单位时间内经过这区域流向n 所指向一侧的液体的质量P（液体得密度为）。

（a）（b）图5－11解该斜柱体的斜高｜v |，斜高与地面垂线的夹角为v与n的夹角，所以这柱体的高为｜v｜cos，体积为A｜v｜cos=A v·n。

2 点的坐标与向量的坐标例1 已知点A(4，1，7）、B(-3，5,0）,在y轴上求一点M，使得|MA｜=|MB｜。

解因为点在y轴上,故设其坐标为，则由两点间的距离公式,有解得，故所求点为例2 求证以三点为顶点的三角形是一个等腰三角形.解因为所以，即△为等腰三角形。

5.2。

2 向量运算的坐标表示例3 设有点，，求向量的坐标表示式.解由于，而，,于是即例4 已知两点A(4，0,5）和B（7，1，3)，求与方向相同的单位向量e。

解因为＝–＝（7，1,3）－（4，0，5）＝（3，1，–2），所以＝，于是 e.例5 求解以向量为未知元的线性方程组其中a＝(2，1，2），b=(—1，1，-2).解解此方程组得x=2a–3b , y =3a–5b以a，b代入，即得x=2(2,1,2)–3(–1,1，–2）=（7,–1,10)y=3(2，1,2)–5（–1,1,–2)=(11,–2,16)。

(完整版)高等数学空间解析几何与向量代数练习题与答案

空间解析几何与矢量代数小练习一填空题 5’x9=45分1、平行于向量a=(6,7,-6)的单位向量为______________.2、设已知两点M1(4,2,1)和M2(3,0,2)，计算向量M1M2的模_________________，方向余弦_________________和方向角_________________3、以点(1,3,-2)为球心，且通过坐标原点的球面方程为__________________.4、方程x2+y2+z2-2x+4y+2z=0表示______________曲面.5、方程x2+y2=z表示______________曲面.6、x2+y2=z2表示______________曲面.7、在空间解析几何中y=x2表示______________图形.二计算题 11’x5=55分1、求过点(3,0,-1)且与平面3x-7y+5z-12=0平行的平面方程.2、求平行于x轴且过两点(4,0,-2)和(5,1,7)的平面方程.3、求过点(1,2,3)且平行于直线x y-3z-12=1=5的直线方程.4、求过点(2,0,-3)且与直线⎧⎨x-2y+4z-7=0⎩3x+5y-2z+1=0垂直的平面方5、已知：OA=ϖi+3kϖ，OB=ϖj+3kϖ，求∆OAB的面积。

参考答案一填空题1、±⎨⎧67-6⎫⎩11,11,11⎬⎭2、M 11M 2=2,cos α=-2,cos β=22,cos γ=12,α=2π3,β=3ππ4,γ=33、(x -1)2+(y -3)2+(z +2)2=144、以(1,-2,-1)为球心,半径为6的球面5、旋转抛物面6、圆锥面7、抛物柱面二计算题1、3x -7y +5z -4=02、9y -z -2=03、x -1y -2z -32=1=5 4、16x -14y -11z -65=05S ∆=12OA ⨯OB =192。

高三数学空间向量试题答案及解析

高三数学空间向量试题答案及解析1.如图，长方体中，分别为中点，（1）求证：．（2）求二面角的正切值．【答案】（1）见解析（2）【解析】（1）由长方体及E、F分别为AB、C1D1的中点知，AE平行且等于C1F，所以AEC1F是平行四边形，所以C1E∥AF，由线面平行的判定定理知，C1E∥面ACF；（2）易证FG⊥面ABCD，过F作FH⊥AC于H，连结HG，因为FG⊥面ABCD，则FG⊥AC，所以∠FHG为二面角F—AC—G的平面角，然后通过解三角形，求出FG、GH的长，即可求出∠FHG的正切值，即为二面角F-AC-G的正切值.试题解析：(1)证明：在长方体中，分别为中点，且四边形是平行四边形3分，5分(2)．长方体中，分别为中点，7分过做于，又就是二面角的平面角 9分，在中， 11分直角三角形中 13分二面角的正切值为 14分考点:线面平行的判定定理；二面角的计算；逻辑推理能力2.如图，在直三棱柱A1B1C1－ABC中，AB⊥AC，AB＝AC＝2，A1A＝4，点D是BC的中点．(1)求异面直线A1B与C1D所成角的余弦值；(2)求平面ADC1与平面ABA1夹角的正弦值．【答案】（1）（2）【解析】解：(1)以A为坐标原点，建立如图所示的空间直角坐标系A－xyz，则A(0,0,0)，B(2,0,0)，C(0,2,0)，D(1,1,0)，A1(0,0,4)，C1(0,2,4)，∴＝(2,0，－4)，＝(1，－1，－4)．∵cos〈，〉＝＝＝，∴异面直线A1B与C1D所成角的余弦值为.(2)设平面ADC1的法向量为n1＝(x，y，z)，∵＝(1,1,0)，＝(0,2,4)，∴n1·＝0，n 1·＝0，即x＋y＝0且2y＋4z＝0，取z＝1，得x＝2，y＝－2，∴n1＝(2，－2,1)是平面ADC1的一个法向量．取平面AA1B的一个法向量为n2＝(0,1,0)，设平面ADC1与平面ABA1夹角的大小为θ.由cosθ＝＝＝，得sinθ＝.因此，平面ADC1与平面ABA1夹角的正弦值为.3.已知正方体ABCD－A1B1C1D1中，点E为上底面A1C1的中心，若＝＋x＋y，则x、y的值分别为()A．x＝1，y＝1B．x＝1，y＝C．x＝，y＝D．x＝，y＝1【答案】C【解析】如图，＝＋＝＋＝＋ (＋)．4.如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：(1)·；(2)·；(3)EG的长；(4)异面直线AG与CE所成角的余弦值．【答案】（1）（2）－（3）（4）【解析】解：设＝a，＝b，＝c.则|a|＝|b|＝|c|＝1，〈a，b〉＝〈b，c〉＝〈c，a〉＝60°.＝BD＝c－a，＝－a，＝b－c，(1)·＝(c－a)·(－a)＝a2－a·c＝；(2)·＝ (c－a)·(b－c)＝ (b·c－a·b－c2＋a·c)＝－；(3)＝＋＋＝a＋b－a＋c－b＝－a＋b＋ c.||2＝a2＋b2＋c2－a·b＋b·c－c·a＝.即||＝，所以EG的长为.(4)设、的夹角为θ.＝b＋c，＝＋＝－b＋a，cosθ＝＝－，由于异面直线所成角的范围是(0°，90°]，所以异面直线AG与CE所成角的余弦值为.5.在如图所示的空间直角坐标系中，一个四面体的顶点坐标分别是（0,0,2），（2,2,0），（1,2，1），（2,2,2），给出编号①、②、③、④的四个图，则该四面体的正视图和俯视图分别为（）A．①和②B．③和①C．④和③D．④和②【答案】D【解析】设，在坐标系中标出已知的四个点，根据三视图的画图规则判断三棱锥的正视图为④与俯视图为②，故选D.【考点】空间由已知条件，在空间坐标系中作出几何体的形状，再正视图与俯视图，容易题.6.如图，直四棱柱底面直角梯形，∥，，是棱上一点，，，，，.（1）求异面直线与所成的角；（2）求证：平面.【答案】(1);（2）证明见解析.【解析】（1）本题中由于有两两垂直，因此在求异面直线所成角时，可以通过建立空间直角坐标系，利用向量的夹角求出所求角；（2）同（1）我们可以用向量法证明线线垂直，以证明线面垂直，，，，易得当然我们也可直线用几何法证明线面垂直，首先，这由已知可直接得到，而证明可在直角梯形通过计算利用勾股定理证明，，，因此，得证.（1）以原点，、、分别为轴、轴、轴建立空间直角坐标系.则，，，. 3分于是,,,异面直线与所成的角的大小等于. 6分（2）过作交于，在中，，，则，，，， 10分，.又，平面. 12分【考点】（1）异面直线所成的角；（2）线面垂直.7.（2013•天津）如图，四棱柱ABCD﹣A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD=CD=1，AA1=AB=2，E为棱AA1的中点．（1）证明B1C1⊥CE；（2）求二面角B1﹣CE﹣C1的正弦值．（3）设点M在线段C1E上，且直线AM与平面ADD1A1所成角的正弦值为，求线段AM的长．【答案】（1）见解析（2）（3）【解析】（1）证明：以点A为原点建立空间直角坐标系，如图，依题意得A（0，0，0），B（0，0，2），C（1，0，1），B1（0，2，2），C1（1，2，1），E（0，1，0）．则，而=0．所以B1C1⊥CE；（2）解：，设平面B1CE的法向量为，则，即，取z=1，得x=﹣3，y=﹣2．所以．由（1）知B1C1⊥CE，又CC1⊥B1C1，所以B1C1⊥平面CEC1，故为平面CEC1的一个法向量，于是=．从而==．所以二面角B1﹣CE﹣C1的正弦值为．（3）解：，设0≤λ≤1，有．取为平面ADD1A1的一个法向量，设θ为直线AM与平面ADD1A1所成的角，则==．于是．解得．所以．所以线段AM的长为．8.如图，四棱锥P-ABCD中，PA⊥平面ABCD，E为BD的中点，G为PD的中点，△DAB≌△DCB，EA=EB=AB=1，PA=，连接CE并延长交AD于F.（1）求证：AD⊥平面CFG；（2）求平面BCP与平面DCP的夹角的余弦值.【答案】（1）见解析（2）【解析】（1）因为△DAB ≌△DCB，EA=EB=AB=1，所以△ECB是等边，,（2）建立空间坐标系如图，取向观点的坐标为, 向量设平面PBC的法向量平面PDC的法向量则【考点】本题主要考查空间垂直关系的证明、平行关系的运用，考查空间角的求解方法，考查空间想象能力、推理论证能力、计算能力.9.如图，四棱锥P-ABCD中，底面ABCD为平行四边形，∠DAB=60°,AB=2AD,PD⊥底面ABCD.（1）证明：PA⊥BD；（2）若PD=AD，求二面角A-PB-C的余弦值。

高三数学空间向量试题答案及解析

高三数学空间向量试题答案及解析1.如图，在四棱锥中，底面，，，，，点为棱的中点.（Ⅰ）证明：；（Ⅱ）若为棱上一点，满足，求二面角的余弦值.【答案】（Ⅰ）详见解析；（Ⅱ）余弦值为.【解析】思路一：坐标法.依题意，以点为原点建立空间直角坐标系（如图），写出各点的坐标，利用空间向量即可解决问题.思路二：几何法.（Ⅰ）如图，取中点，连接，.易得四边形为矩形，从而使问题得证.（Ⅱ）由于，那么BF在平面ABCD内的射影与AC垂直，故考虑作出BF在平面ABCD 内的射影.在中，过点作交于点.由题设可得，从而得，.在平面内，作交于点，于是.显然为二面角的平面角. 在三角形PAG中，由余弦定理可得二面角的余弦值.试题解析：解法一：坐标法.依题意，以点为原点建立空间直角坐标系（如图），可得，，，.由为棱的中点，得.（Ⅰ）向量，，故. 所以，.（Ⅱ）向量，，，.由点在棱上，设，.故.由，得，因此，，解得.即.设为平面的法向量，则即不妨令，可得为平面的一个法向量取平面的法向量，则.易知，二面角是锐角，所以其余弦值为.解法二：几何法.（Ⅰ）如图，取中点，连接，.由于分别为的中点，故，且，又由已知，可得且，故四边形为平行四边形，所以.因为底面，故，而，从而平面，因为平面，于是，又，所以.（Ⅱ）如图，在中，过点作交于点.因为底面，故底面，从而.又，得平面，因此.在底面内，可得，.在平面内，作交于点，于是.由于，故，所以四点共面.由，，得平面，故.所以为二面角的平面角.在中，，，，由余弦定理可得，在三角形PAG中，由余弦定理得.所以，二面角的余弦值为.【考点】1、空间直线的垂直关系；2、二面角.2.在如图所示的多面体中，四边形和都为矩形.（Ⅰ）若，证明：直线平面；（Ⅱ）是否存在过的平面，使得直线平行，若存在请作出平面并证明，若不存在请说明理由.【答案】（Ⅰ）见解析；（Ⅱ）存在，证明见解析【解析】（Ⅰ）由四边形和都为矩形知，⊥AB，⊥AC，由线面垂直判定定理知⊥面ABC，由线面垂直定义知⊥BC，又因为AC⊥BC，由线面垂直判定定理知，BC⊥面；（Ⅱ）取AB的中点为M，连结交于D，连结DE，显然E是的中点，根据三角形中位线定理得，DE∥，又由于DE在面过的平面内，根据线面平行的判定定理知和该平面平行.试题解析：（Ⅰ）证明：因为四边形和都是矩形，所以 2分因为为平面内的两条相交直线，所以 4分因为直线平面，所以又由已知，为平面内的两条相交直线，所以平面 7分（Ⅱ）存在 8分连接，设，取线段AB的中点M，连接.则平面为为所求的平面. 1１分由作图可知分别为的中点，所以 13分又因为因此 14分考点: 空间线面垂直垂直的判定与性质；线面平行的判定；推理论证能力3.平面α经过三点A(－1,0,1)，B(1,1,2)，C(2，－1,0)，则下列向量中与平面α的法向量不垂直的是()A．(，－1，－1)B．(6，－2，－2)C．(4,2,2)D．(－1,1,4)【答案】D【解析】设平面α的法向量为n，则n⊥，n⊥，n⊥，所有与 (或、)平行的向量或可用与线性表示的向量都与n垂直，故选D.4.如图所示，已知空间四边形OABC中，|OB|＝|OC|，且∠AOB＝∠AOC，则、夹角θ的余弦值为()A．0B．C．D．【答案】A【解析】设＝a，＝b，＝c.由已知条件∠AOB＝∠AOC，且|b|＝|c|，·＝a·(c－b)＝a·c－a·b＝|a||c|cos∠AOC－|a||b|cos∠AOB＝0，∴cosθ＝0.故选A.5.若向量a＝(1,1，x)，b＝(1,2,1)，c＝(1,1,1)，满足条件(c－a)·(2b)＝－2，则x＝________.【答案】2【解析】c－a＝(0,0,1－x)，2b＝(2,4,2)，由(c－a)·(2b)＝－2，得(0,0,1－x)·(2,4,2)＝－2，即2(1－x)＝－2，解得x＝2.6.如图所示，已知空间四边形ABCD的每条边和对角线长都等于1，点E、F、G分别是AB、AD、CD的中点，计算：(1)·；(2)·；(3)EG的长；(4)异面直线AG与CE所成角的余弦值．【答案】（1）（2）－（3）（4）【解析】解：设＝a，＝b，＝c.则|a|＝|b|＝|c|＝1，〈a，b〉＝〈b，c〉＝〈c，a〉＝60°.＝BD＝c－a，＝－a，＝b－c，(1)·＝(c－a)·(－a)＝a2－a·c＝；(2)·＝ (c－a)·(b－c)＝ (b·c－a·b－c2＋a·c)＝－；(3)＝＋＋＝a＋b－a＋c－b＝－a＋b＋ c.||2＝a2＋b2＋c2－a·b＋b·c－c·a＝.即||＝，所以EG的长为.(4)设、的夹角为θ.＝b＋c，＝＋＝－b＋a，cosθ＝＝－，由于异面直线所成角的范围是(0°，90°]，所以异面直线AG与CE所成角的余弦值为.7.已知点A(1，t，－1)关于x轴的对称点为B，关于xOy平面的对称点为C，则BC中点D的坐标为________．【答案】(1,0,1)【解析】因为A(1，t，－1)关于x轴的对称点为B(1，－t,1)，关于xOy平面的对称点为C(1，t,1)，所以BC中点D的坐标为(，，)，即D(1,0,1)．8.直三棱柱ABC-A1B1C1中，∠BCA=90°，M，N分别是A1B1，A1C1的中点，BC=CA=CC1，则BM与AN所成的角的余弦值为（）A．B．C．D．【答案】C【解析】以C为原点，直线CA为x轴，直线CB为y轴，直线为轴，则设CA=CB=1，则，，A（1，0，0），，故，，所以，故选C.【考点】本小题主要考查利用空间向量求线线角，考查空间向量的基本运算，考查空间想象能力等数学基本能力，考查分析问题与解决问题的能力.9.如图，已知四棱锥P-ABCD的底面ABCD是菱形，且PC⊥平面ABCD，PC＝AC＝2,E是PA 的中点。

(完整word版)高三数学空间向量专题复习附答案

一、利用向量处理平行与垂直问题例1、在直三棱柱111C B A ABC -中，090=∠ACB , 030=∠BAC ,M A A BC ,6,11==是1CC 得中点。

求证：AM B A ⊥1练习：棱长为a 的正方体ABCD —A 1B 1C 1D 1中，在棱DD 1上是否存在点P 使B 1D ⊥面P AC ？例2 如图，已知矩形ABCD 和矩形ADEF 所在平面互相垂直，点N M ,分别在对角线AE BD ,上，且AE AN BD BM 31,31==,求证：//MN 平面CDE练习1、在正方体1111D C B A ABCD -中,E,F 分别是BB 1,,CD 中点，求证：D 1F ⊥平面ADE2、如图，在底面是菱形的四棱锥P —ABCD 中, ︒=∠60ABC ，,2,a PD PB a AC PA ====点E 在PD 上,且PE :ED = 2: 1.在棱PC 上是否存在一点F, 使BF ∥平面AEC?证明你的结论.二、利用空间向量求空间的角的问题例1 在正方体1111D C B A ABCD -中,E 1，F 1分别在A 1B 1,,C 1D 1上，且E 1B 1=41A 1B 1，D 1F 1=41D 1C 1，求BE 1与DF 1所成的角的大小。

例2 在正方体1111D C B A ABCD -中, F 分别是BC 的中点，点E 在D 1C 1上,且=11E D 41D 1C 1,试求直线E 1F 与平面D 1AC例3 在正方体1111D C B A ABCD -中,求二面角1C BD A --的大小。

zx1CFD CBA例4 已知E,F分别是正方体1111DCBAABCD-的棱BC和CD的中点，求：（1）A1D与EF所成角的大小；（2）A1F与平面B1EB所成角的大小；（3）二面角BBDC--11的大小。

三、利用空间向量求空间的距离的问题例1 直三棱柱AB C-A1B1C1的侧棱AA1，底面ΔAB C求点B1到平面A1B C的距离。

(完整word版)高三数学空间向量专题复习附答案

一、利用向量处理平行与垂直问题例1、在直三棱柱111C B A ABC -中，090=∠ACB , 030=∠BAC ,M A A BC ,6,11==是1CC 得中点。

三、利用空间向量求空间的距离的问题例1 直三棱柱AB C-A1B1C1的侧棱AA1，底面ΔAB C求点B1到平面A1B C的距离。

高中数学空间向量经典例题及解析

高中数学空间向量经典例题及解析一、引言空间向量是高中数学的一个重要知识点，它涉及到三维空间中向量的加法、数乘、数量积和向量积等运算。

这些运算在解决实际问题中有着广泛的应用，因此学好空间向量对于学生来说至关重要。

本篇文章将通过经典例题的方式，对空间向量的相关知识点进行深入解析，以期帮助学生更好地掌握这一知识点。

二、经典例题及解析【例题1】在空间四边形中，已知两个向量，，求异面直线的夹角(锐角或直角)。

【解析】本题考查空间向量的夹角问题，需要利用两个向量的夹角公式。

【解答】首先根据向量的定义，可得到向量，的坐标分别为(, )。

根据向量的加法，可得向量的坐标为(, )。

又因为两个向量垂直，所以它们的数量积为0，即，所以。

根据异面直线夹角公式，可得异面直线的夹角为。

【例题2】在长方体中，已知三个向量，，求异面直线的夹角(锐角或直角)。

【解析】本题除了需要用到向量的加法、数乘、数量积和向量积等运算，还需要用到长方体的性质。

【解答】首先根据向量的定义，可得到向量的坐标分别为(, , )。

又因为长方体中，所以可以表示为和的线性组合，即或。

设所在直线的方向向量，所在平面的法向量，则的坐标分别为(, )。

根据向量夹角公式和向量垂直的条件，可得垂直于平面，所以。

又因为两个向量垂直，所以它们的数量积为0，即，所以。

根据异面直线夹角公式，可得异面直线AB与CD的夹角为。

【例题3】已知长方体，设点，求与平面之间的距离。

【解析】本题需要利用长方体的性质和向量的数量积求解。

【解答】设平面的法向量，则所在直线的方向向量。

因为点在平面内，所以点在平面外，所以向量，即。

又因为向量与平面共线，所以向量，即。

根据向量的数量积和点到平面的距离公式，可得与平面之间的距离为。

三、总结空间向量是高中数学的一个难点也是重点，通过经典例题的解析，我们可以更好地掌握空间向量的相关知识点。

在解决实际问题时，我们需要灵活运用向量的加法、数乘、数量积和向量积等运算，同时还要注意向量的表示和坐标的确定。

空间向量立体几何(绝对经典)

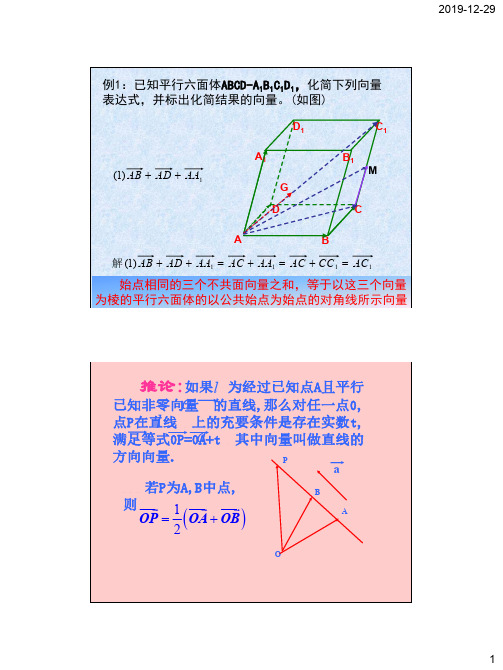
例1：已知平行六面体ABCD-A 1B 1C 1D 1，化简下列向量表达式，并标出化简结果的向量。

(如图)A BCD A 1B 1C 1D 1G1)1(AA AD AB ++1111)1(AC CC AC AA AC AA AD AB =+=+=++解M 始点相同的三个不共面向量之和，等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量推论:如果为经过已知点A且平行已知非零向量的直线,那么对任一点O,点P在直线上的充要条件是存在实数t,满足等式OP=OA+t 其中向量叫做直线的方向向量.ll aaOABP a若P为A,B中点,则()12=+ OP OA OB2.共面向量定理:如果两个向量不共线,则向量与向量共面的充要条件是存在实数对使, a b yx , p ,a b OM a b A B A 'Pp p xa yb =+ 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使或对空间任一点O,有=+MP xMA yMB =++ OP OM xMA yMB 注意：空间四点P 、M 、A 、B 共面⇔存在唯一实数对,,x y MP xMA yMB =+ （）使得(1)OP xOM yOA zOB x y z ⇔=++++= 其中，例1：已知m,n 是平面α内的两条相交直线，直线l 与α的交点为B ，且l ⊥m ，l ⊥n ，求证：l ⊥α。

n mg g m n αl l 证明：在α内作不与m、n重合的任一条直线g,在l、m、n、g上取非零向量l、m、n、g ，因m与n相交，得向量m、n 不平行，由共面向量定理可知，存在唯一的有序实数对（x，y），使g =x m +y n ,l ·g =x l ·m +y l ·n∵ l ·m =0,l ·n =0∴ l ·g =0∴ l⊥g∴ l⊥g这就证明了直线l垂直于平面α内的任一条直线，所以l⊥α巩固练习：利用向量知识证明三垂线定理αa A O P ().,0,,,,0,0,PA a PA a a OA a PO a PA OAy PO x PA y x OA PO OA PO a OA a OA a PO a PO PO aa ⊥⊥∴=⋅+⋅=⋅∴+==⋅∴⊥=⋅∴⊥∴⊥即使有序实数对定理可知，存在唯一的不平行，由共面向量相交，得又又而上取非零向量证明：在αPA a OAa a PA OA PA PO ⊥⊥⊂求证：且内的射影，在是的垂线，斜线，分别是平面已知：,,ααα复习:2. 向量的夹角:a bO ABabθ0a b π≤≤ ，a b ，向量的夹角记作:a b 与a b = ||||cos ,a b a b 1.空间向量的数量积:111222(,,),(,,)a x y z b x y z == 设121212x x y y z z =++cos ||||a ba b a b =，121212222222111222++=++⋅++x x y y z z x y z x y z 5.向量的模长:2222||a a x y z ==++ (,,)a x y z = 设4.有关性质:(1)两非零向量111222(,,),(,,)a x y zb x y z == 1212120x x y y z z ++=0a b a b ⊥⇔=⇔ (2)||||||a b a b ≤ ||||,a b a b a b =⇒ 同方向||||,a b a b a b =-⇒ 反方向注意：此公式的几何意义是表示长方体的对角线的长度。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例1 已知长方体ABCD -A 1B 1C 1D 1中，棱长AB =BC =3，BB 1=4，连结B 1C ，过B 点作B 1C 的垂线交CC 1于点E ，交B 1C 于点F ．
（1）求证：A 1C ⊥平面EBD ；
（2）设A 1C ∩平面EBD =K ，求线段A 1K 的长；（3）求A 1B 与平面BDE 所成角的大小．
解法1：（1）证BE C A ⊥1，BD C A ⊥1，可得A 1C ⊥平面EBD ．
（2）在平面1BC 中用平几知识可求得4
9
=
CE ，在对角面1AC 中，设AC 与BD 交于点O ，可求得22CE OC OE +=4173=，由面积法得34
34
9=CK ，
2
121AA AC C A +=34=，34
342511=
-=CK C A K A ．（3）∵A 1C ⊥平面B DE ，∴∠A 1BK 就是所求的直线A 1B 与平面BDE 所成的角． ∴BK A 1sin ∠B A K A 11=
34345=
，∴直线A 1B 与平面BDE 所成的角为34
34
5arcsin ．解法2：（1）以D 为原点，DA 、DC 、DD 1所在直线分别为x 轴，y 轴，
z 轴建立空间直角坐标系D-xyz ，则D (0，0，0），A (3，0，0），C (0，3，0），B (3，3，0），A 1(3，0，4），D 1(0，0，4），C 1(0，3，4），
B 1(3，3，4）．
设E (0，3，z ），则∵BE ⊥B 1C ，∴BE ·C B 1=0，BE =(-3，0，z ），B 1=(-3，0，-4），
∴·B 1C=(-3，0，z ）·（-3，0，-4）=9-4z=0，∴z=49
， ∴E(0，3，4
9)， ∴A 1·=-3×3+3×3=0，A 1·=3×3-4×4
9=0，
∴A 1⊥，A 1⊥，∴A 1⊥DB ，A 1C ⊥DE ， ∴A 1C ⊥平面BDE ．（2）DK =m +n =m (3，3，0）+n （0，3，49）=(3m ，3m +3n ，4
9n ）， ∴K (3m ，3m +3n ，49n ），∴A 1=（3m -3，3m +3n ，4
9n-4），
A 1⊥⇔A 1·=(3m -3，3m +3n ，
4
9
n -4）·(3，3，0）=0， A
B
C
D
1
A 1
B 1
C 1
D E
F
y
∴2m +n -1=0，及=A 1⊥⇔·=(3m-3，3m+3n ，49
n-4）·(0，3，4
9）=0，
∴16m +25n -16=0，∴m =34
9
，n =178， ∴K （-3475，3475，-1750）=K A 1，
∴|A 1|=
34
34
25这就是所求的线段A 1K 的长．（3）∵A 1C ⊥平面BDE ，∴∠CA 1B 就是所求的直线A 1B 与平面BDE 所成的角的余角．
A 1=（0，3，-4），|A 1|=5，∴sin
∠A 1BK =
=
34
34
5，∴sin ∠A 1BK =arcsin=
34345，
即直线A 1B 与平面BDE 所成的角的大小为arcsin 为
34
34
5．例2．用向量法解题（请按照图形，建立坐标系）：正四棱锥S ABCD -中，所有棱长都是2，P 为SA 的中点．
（1）求二面角B SC D --的大小；
（2）如果点Q 在棱SC 上，那么直线BQ 与PD 由．
解：（1）取SC 的中点E ，连结,BE DE ，SCB ∆∆Q 与角形，
∴SC BE ⊥，SC DE ⊥，∴BED ∠是二面角B SC D --的平面角，在BED ∆中，
2223381cos 263
BE DE BD BED BE DE +-+-∠===-⋅，
∴1arccos 3BED π∠=-，故二面角B SC D --的大小为1
arccos 3
π-．
（2）设AC BD O =I ，以射线,,OA OB OS 分别为,,x y z 轴建立空间直角坐标系，
设CQ x =，则(0,B D ，(
()2222
P Q x x -，
(()2222
DP BQ x x ==u u u r u u u r ，30DP BQ x ⋅=-≠u u u r u u u r （∵0[∈x ，
]2，∴BQ 与PD 不可能垂直．。

高数空间几何向量典型例题

高等数学 向量代数与空间解析几何题【精选文档】

(完整版)高等数学空间解析几何与向量代数练习题与答案

高三数学空间向量试题答案及解析

高三数学空间向量试题答案及解析

(完整word版)高三数学空间向量专题复习附答案

(完整word版)高三数学空间向量专题复习附答案

高中数学空间向量经典例题及解析

空间向量立体几何(绝对经典)

高等数学向量代数与空间解析几何题【精选文档】