实验一 信号的时域采样和时域分析
信号的时域分析

量化级数的选择
总结词
量化级数的选择决定了信号离散化的程度,它影响着量化误 差的大小和数据表示的精度。
详细描述
量化级数越多,每个级别所代表的幅度范围越小,从而减小 了量化误差。但同时,更多的量化级数会增加数据表示的复 杂度和存储需求。在实际应用中,需要根据对信号精度和系 统资源的需求来权衡量化级数的选择。
带通滤波器
总结词
带通滤波器用于保留信号中的特定频率范围的信号, 抑制其他频率成分。
详细描述
带通滤波器允许某一频率范围内的信号通过,而抑制该 范围之外的信号。在时域分析中,带通滤波器常用于提 取特定频率的信号特征、消除干扰等。
带阻滤波器
总结词
带阻滤波器用于抑制信号中的特定频率范围的信号,保留其他频 率成分。
采样率的选择
总结词
采样率的选择对于信号的时域分析至关重要,它决定了采样点之间的时间间隔,进而影响信号的精度 和失真程度。
详细描述
采样率越高,采样点之间的时间间隔越小,能够捕获到的信号细节越多,但同时也会增加数据量和处 理复杂度。反之,采样率过低会导致信号失真,无法准确反映原始信号的特征。因此,需要根据实际 需求和系统资源来选择合适的采样率。
信号的时域分析
目
CONTENCT
录
• 信号的概述 • 信号的时域特性 • 信号的时域分析方法 • 信号的时域变换 • 信号的时域滤波 • 信号的时域采样与量化
01
信号的概述
信号的定义
信号的定义
信号是传递信息的一种方式,通常由数据、文本、声音、图像等 形式表示。在电子工程和通信领域中,信号是用来传输信息的物 理量,可以是电信号、光信号等。
信号的相位
相位
表示信号在时间上的相对位置,通常用相位角来描述。相位角的变化会影响信 号的波形和时间关系。
数字信号处理实验报告

实验一 信号、系统及系统响应一、实验目的1、熟悉理想采样的性质,了解信号采样前后的频谱变化,加深对时域采样定理的理解。
2、熟悉离散信号和系统的时域特性。
3、熟悉线性卷积的计算编程方法:利用卷积的方法,观察、分析系统响应的时域特性。
4、掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对离散信号、系统及其系统响应进行频域分析。
二、 实验原理1.理想采样序列:对信号x a (t)=A e −αt sin(Ω0t )u(t)进行理想采样,可以得到一个理想的采样信号序列x a (t)=A e −αt sin(Ω0nT ),0≤n ≤50,其中A 为幅度因子,α是衰减因子,Ω0是频率,T 是采样周期。
2.对一个连续时间信号x a (t)进行理想采样可以表示为该信号与一个周期冲激脉冲的乘积,即x ̂a (t)= x a (t)M(t),其中x ̂a (t)是连续信号x a (t)的理想采样;M(t)是周期冲激M(t)=∑δ+∞−∞(t-nT)=1T ∑e jm Ωs t +∞−∞,其中T 为采样周期,Ωs =2π/T 是采样角频率。
信号理想采样的傅里叶变换为X ̂a (j Ω)=1T ∑X a +∞−∞[j(Ω−k Ωs )],由此式可知:信号理想采样后的频谱是原信号频谱的周期延拓,其延拓周期为Ωs =2π/T 。
根据时域采样定理,如果原信号是带限信号,且采样频率高于原信号最高频率分量的2倍,则采样以后不会发生频率混叠现象。
三、简明步骤产生理想采样信号序列x a (n),使A=444.128,α=50√2π,Ω0=50√2π。
(1) 首先选用采样频率为1000HZ ,T=1/1000,观察所得理想采样信号的幅频特性,在折叠频率以内和给定的理想幅频特性无明显差异,并做记录;(2) 改变采样频率为300HZ ,T=1/300,观察所得到的频谱特性曲线的变化,并做记录;(3) 进一步减小采样频率为200HZ ,T=1/200,观察频谱混淆现象是否明显存在,说明原因,并记录这时候的幅频特性曲线。
信号资源分析实验报告(3篇)

第1篇一、实验目的1. 理解信号资源的基本概念和分类。
2. 掌握信号采集、处理和分析的方法。
3. 分析不同信号资源的特点和适用场景。
4. 提高信号处理和分析的实际应用能力。
二、实验背景信号资源在通信、遥感、生物医学等领域具有广泛的应用。
本实验通过对不同类型信号资源的采集、处理和分析,使学生了解信号资源的基本特性,掌握信号处理和分析的方法。
三、实验内容1. 信号采集(1)实验设备:信号发生器、示波器、数据采集卡、计算机等。
(2)实验步骤:1)使用信号发生器产生正弦波、方波、三角波等基本信号。
2)将信号通过数据采集卡输入计算机,进行数字化处理。
3)观察示波器上的波形,确保采集到的信号准确无误。
2. 信号处理(1)实验设备:MATLAB软件、计算机等。
(2)实验步骤:1)利用MATLAB软件对采集到的信号进行时域分析,包括信号的时域波形、平均值、方差、自相关函数等。
2)对信号进行频域分析,包括信号的频谱、功率谱、自功率谱等。
3)对信号进行滤波处理,包括低通、高通、带通、带阻滤波等。
4)对信号进行时频分析,包括短时傅里叶变换(STFT)和小波变换等。
3. 信号分析(1)实验设备:MATLAB软件、计算机等。
(2)实验步骤:1)分析不同类型信号的特点,如正弦波、方波、三角波等。
2)分析信号在不同场景下的应用,如通信、遥感、生物医学等。
3)根据实验结果,总结信号资源的特点和适用场景。
四、实验结果与分析1. 时域分析(1)正弦波信号:具有稳定的频率和幅度,适用于通信、测量等领域。
(2)方波信号:具有周期性的脉冲特性,适用于数字信号处理、数字通信等领域。
(3)三角波信号:具有平滑的过渡特性,适用于模拟信号处理、音频信号处理等领域。
2. 频域分析(1)正弦波信号:频谱只有一个频率成分,适用于通信、测量等领域。
(2)方波信号:频谱包含多个频率成分,适用于数字信号处理、数字通信等领域。
(3)三角波信号:频谱包含多个频率成分,适用于模拟信号处理、音频信号处理等领域。
时域分析实验报告

时域分析实验报告引言时域分析是一种信号处理技术,用于研究信号在时间上的变化。
通过时域分析,我们可以观察信号的幅度、频率、相位和周期等特征。
本实验旨在通过使用适当的时域分析方法,对给定的信号进行分析,并探讨不同方法的优缺点。
实验目的1.了解时域分析的基本概念和原理;2.掌握常见的时域分析方法,并理解它们的适用范围;3.通过实验验证不同的时域分析方法的有效性。
实验步骤1.准备实验所需的信号。
可以选择不同类型的信号,如正弦信号、方波信号或脉冲信号等。
确保信号的采样频率足够高,以避免采样失真。
2.使用示波器或数据采集卡等设备,将信号输入计算机中进行处理和分析。
3.基本时域分析方法:–平均值和标准差:计算信号的平均值和标准差,以了解信号的中心位置和离散程度。
–自相关函数:计算信号与自身的相关性,用于分析信号的周期性。
–傅里叶变换:将信号转换到频域,以获得信号的频谱信息。
–卷积:用于信号的滤波和信号与系统的响应分析。
4.根据实验需要选择适当的时域分析方法进行信号处理和分析。
可以结合不同的方法,以获得更全面的信号特征信息。
实验结果与讨论1.绘制信号的波形图,并观察信号的幅度、频率和相位特征。
2.计算信号的平均值和标准差,并分析信号的中心位置和离散程度。
3.计算信号的自相关函数,并观察信号的周期性。
根据自相关函数的峰值位置和间距,可以估计信号的周期。
4.对信号进行傅里叶变换,并观察信号的频谱特征。
可以通过傅里叶变换结果分析信号的频率成分和能量分布。
5.使用卷积方法对信号进行滤波,并观察滤波效果。
可以选择合适的滤波器来去除信号中的噪声或不需要的频率成分。
6.对比不同的时域分析方法,分析它们在信号处理和分析中的优缺点。
根据实验结果,选择适合特定场景的方法。
结论通过时域分析实验,我们深入了解了时域分析的基本概念和原理,并掌握了常见的时域分析方法。
通过对信号的处理和分析,我们可以获得信号的重要特征信息,如幅度、频率、相位和周期等。
大学信号分析实验报告

一、实验目的1. 理解信号分析的基本概念和原理;2. 掌握信号的时域和频域分析方法;3. 熟悉MATLAB在信号分析中的应用;4. 培养实验操作能力和数据分析能力。
二、实验原理信号分析是研究信号特性的科学,主要包括信号的时域分析和频域分析。
时域分析关注信号随时间的变化规律,频域分析关注信号中不同频率分量的分布情况。
1. 时域分析:通过对信号进行采样、时域卷积、微分、积分等操作,分析信号的时域特性。
2. 频域分析:通过对信号进行傅里叶变换、频域卷积、滤波等操作,分析信号的频域特性。
三、实验内容1. 信号采集与处理(1)采集一段语音信号,利用MATLAB的录音功能将模拟信号转换为数字信号。
(2)对采集到的信号进行采样,选择合适的采样频率,确保满足奈奎斯特采样定理。
(3)绘制语音信号的时域波形图,观察信号的基本特性。
2. 信号频谱分析(1)对采集到的信号进行傅里叶变换,得到信号的频谱。
(2)绘制信号的频谱图,分析信号的频域特性。
3. 信号滤波(1)设计一个低通滤波器,滤除信号中的高频噪声。
(2)将滤波后的信号与原始信号进行对比,分析滤波效果。
4. 信号调制与解调(1)对原始信号进行幅度调制,产生已调信号。
(2)对已调信号进行解调,恢复原始信号。
(3)分析调制与解调过程中的信号变化。
四、实验步骤1. 采集语音信号,将模拟信号转换为数字信号。
2. 对采集到的信号进行采样,确保满足奈奎斯特采样定理。
3. 绘制语音信号的时域波形图,观察信号的基本特性。
4. 对信号进行傅里叶变换,得到信号的频谱。
5. 绘制信号的频谱图,分析信号的频域特性。
6. 设计低通滤波器,滤除信号中的高频噪声。
7. 对滤波后的信号与原始信号进行对比,分析滤波效果。
8. 对原始信号进行幅度调制,产生已调信号。
9. 对已调信号进行解调,恢复原始信号。
10. 分析调制与解调过程中的信号变化。
五、实验结果与分析1. 时域分析通过观察语音信号的时域波形图,可以看出信号的基本特性,如信号的幅度、频率等。
数字信号处理第三版用MATLAB上机实验

实验二:时域采样与频域采样一、时域采样1.用MATLAB编程如下:%1时域采样序列分析fs=1000A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=1000;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,1);stem(n,xn);xlabel('n,fs=1000Hz');ylabel('xn');title('xn');subplot(3,2,2);plot(n,abs(Xk));xlabel('k,fs=1000Hz'); title('|X(k)|');%1时域采样序列分析fs=200A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=200;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs);Xk=fft(xn);subplot(3,2,3);stem(n,xn);xlabel('n,fs=200Hz'); ylabel('xn');title('xn');subplot(3,2,4);plot(n,abs(Xk));xlabel('k,fs=200Hz'); title('|X(k)|');%1时域采样序列分析fs=500A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=500;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,5);stem(n,xn);xlabel('n,fs=500Hz');ylabel('xn');title('xn');subplot(3,2,6);plot(n,abs(Xk));xlabel('k,fs=500Hz'); title('|X(k)|');2.经调试结果如下图:20406080-200200n,fs=1000Hzxnxn2040608005001000k,fs=1000Hz|X (k)|51015-2000200n,fs=200Hzx nxn510150100200k,fs=200Hz |X(k)|10203040-2000200n,fs=500Hzx nxn102030400500k,fs=500Hz|X (k)|实验结果说明:对时域信号采样频率必须大于等于模拟信号频率的两倍以上,才 能使采样信号的频谱不产生混叠.fs=200Hz 时,采样信号的频谱产生了混叠,fs=500Hz 和fs=1000Hz 时,大于模拟信号频率的两倍以上,采样信号的频谱不产生混叠。
实验一 时域离散信号、系统及系统响应

四、 思考题
• 1 在分析理想采样序列特性的实验中, 采样频率不同时, 相应 在分析理想采样序列特性的实验中, 采样频率不同时, 理想采样序列的傅里叶变换频谱的数字频率度量是否都相同? 理想采样序列的傅里叶变换频谱的数字频率度量是否都相同 它 们所对应的模拟频率是否相同? 为什么? 们所对应的模拟频率是否相同 为什么 • 2 在卷积定理验证的实验中, 如果选用不同的频域采样点数 值, 在卷积定理验证的实验中, 如果选用不同的频域采样点数M值 例如, 例如, 选M=10和M=20, 分别做序列的傅里叶变换, 求得 和 , 分别做序列的傅里叶变换,
• 3 调通并运行实验程序, 完成下述实验内容: 调通并运行实验程序, 完成下述实验内容: 分析采样序列的特性。 ① 分析采样序列的特性。 a. 取采样频率 s=1 kHz, 即T=1 ms。 取采样频率f 。 b. 改变采样频率 fs=300 Hz, 观察 改变采样频率, 的变化, , 观察|X(ejω)|的变化, 并 的变化 做记录(打印曲线 打印曲线); 进一步降低采样频率, 做记录 打印曲线 ; 进一步降低采样频率, fs=200 Hz, , 观察频谱混叠是否明显存在, 说明原因, 并记录(打印 打印) 观察频谱混叠是否明显存在, 说明原因, 并记录 打印 这时的|X(ejω)|曲线。 曲线。 这时的 曲线 • ② 时域离散信号、 系统和系统响应分析。 时域离散信号、 系统和系统响应分析。 a. 观察信号 b(n)和系统 b(n)的时域和频域特性; 利用 观察信号x 和系统h 的时域和频域特性; 和系统 的时域和频域特性 线性卷积求信号x 通过系统h 的响应y(n), 比较 线性卷积求信号 b(n)通过系统 b(n)的响应 通过系统 的响应 , 所求响应y(n)和hb(n)的时域及频域特性, 注意它们之 的时域及频域特性, 所求响应 和 的时域及频域特性 间有无差别, 绘图说明, 并用所学理论解释所得结果。 间有无差别, 绘图说明, 并用所学理论解释所得结果。 b. 观察系统 a(n)对信号 c(n)的响应特性。 观察系统h 对信号x 的响应特性。 对信号 的响应特性 ③ 卷积定理的验证
语音信号处理试验教程
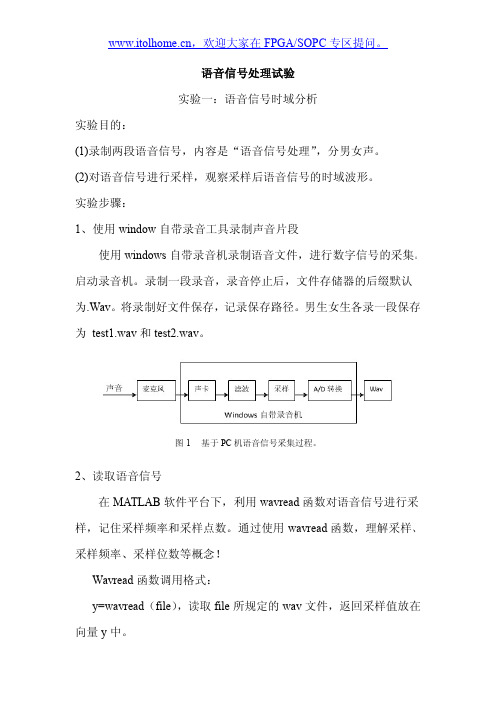
语音信号处理试验实验一:语音信号时域分析实验目的:(1)录制两段语音信号,内容是“语音信号处理”,分男女声。
(2)对语音信号进行采样,观察采样后语音信号的时域波形。
实验步骤:1、使用window自带录音工具录制声音片段使用windows自带录音机录制语音文件,进行数字信号的采集。
启动录音机。
录制一段录音,录音停止后,文件存储器的后缀默认为.Wav。
将录制好文件保存,记录保存路径。
男生女生各录一段保存为test1.wav和test2.wav。
图1基于PC机语音信号采集过程。
2、读取语音信号在MATLAB软件平台下,利用wavread函数对语音信号进行采样,记住采样频率和采样点数。
通过使用wavread函数,理解采样、采样频率、采样位数等概念!Wavread函数调用格式:y=wavread(file),读取file所规定的wav文件,返回采样值放在向量y中。
[y,fs,nbits]=wavread(file),采样值放在向量y中,fs表示采样频率(hz),nbits表示采样位数。
y=wavread(file,N),读取前N点的采样值放在向量y中。
y=wavread(file,[N1,N2]),读取从N1到N2点的采样值放在向量y中。
3、编程获取语音信号的抽样频率和采样位数。
语音信号为test1.wav和test2.wav,内容为“语音信号处理”,两端语音保存到工作空间work文件夹下。
在M文件中分别输入以下程序,可以分两次输入便于观察。
[y1,fs1,nbits1]=wavread('test1.wav')[y2,fs2,nbits2]=wavread('test2.wav')结果如下图所示根据结果可知:两端语音信号的采样频率为44100HZ,采样位数为16。
4、语音信号的时域分析语音信号的时域分析就是分析和提取语音信号的时域参数。
进行语音分析时,最先接触到并且夜市最直观的是它的时域波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一连续信号的时域采样和频域分析班级:021211 学号:02121007 姓名:许多飚成绩:
1实验目的
通过对一个模拟信号进行等间隔时域采样,通过改变采样频率和信号最高截止频率的关系,观察它是否出现频谱混叠,同时求出能够无失真恢复出原模拟信号的最低采样频率。
2 实验内容
对一个余弦信号x(t)=cos(2*pi*f*t),其中f=1Hz,进行理想采样,分别改变采样频率使Fs=2.2Hz, Fs=2.0Hz, Fs=1.8Hz,分别观察它们的时域波形和采样点的位置,对采样点进行傅里叶变换,对采样信号进行频谱分析,观察它们是否出现频谱混叠,同时求出能够无失真恢复出原模拟信号的最低采样频率,即验证奈奎斯特采样频率是否为2Hz。
3实验步骤
Step1. 对余弦信号x(t)=cos(2*pi*f*t),其中f=1Hz,进行理想采样,使采样频率使Fs=2.2Hz,得到它的时域波形和采样波形,对采样点进行傅里叶变换,得到其频谱图;
Step2.改变采样频率,使Fs=2.0Hz, Fs=1.8Hz,重复step1;
Step3. 观察它们是否出现频谱混叠,同时求出能够无失真恢复出原模拟信号的最低采样频率,即验证奈奎斯特采样频率是否为2Hz。
4 程序设计
由于该实验程序简单,故略去程序流图,附代码如下:
5实验结果及分析
1)运行结果
采样频率Fs=2.0Hz
2)实验结果分析
由以上实验结果分析,由于信号频率f=1Hz,
当采样频率Fs=2.2Hz(Fs>2f)时,频谱并未发生混叠现象,进行傅里叶变换后的频谱分析,其频率f=1Hz,能够无失真的恢复原信号;当采样频率Fs=2.0Hz(Fs=2f)时,采样出现临界条件,但依然能够无失真恢复;
当采样频率Fs=1.8Hz(Fs<2f)时,频谱出现混叠现象,进行傅里叶变换后的频谱分析,其频率f=0.8Hz,恢复信号出现失真现象。
3)结论
通过以上对一个正弦信号的时域采样分析,验证时域采样定理不发生频谱混叠的临界条件是最低采样频率(即奈奎斯特采样频率)为信号最高截止频率的2倍。
6总结
通过以上对一个正弦信号的时域采样分析,验证时域采样定理不发生频谱混叠的临界条件是最低采样频率(即奈奎斯特采样频率)为信号最高截止频率的2倍。
在实验中由于要进行对采样信号的频率分析,用到FFT对采样序列进行傅里叶变换,为看到频谱的正式频率和幅值,分别对傅里叶变换后的频率谱进行频移和幅值归一化处理,可以较为清晰地观察到采样序列的频谱。
7参考资料
// 学习相关理论、编写程序及为了完成实验查阅的书籍和文献
// 英文参考文献格式
// 期刊
// [序号] 主要责任者. 文献题名[J]. 刊名, 年, 卷(期): 起止页码.
// 专著、论文集、学位论文、报告
// [序号] 主要责任者. 文献题名[文献类型标识]. 出版地: 出版者, 出版年. 起止页码.。
