3.3垂径定理(1)
3.3垂径定理(1)

CE O
D
如:点C是AB的中点,点D是 ADB 的中点. B
C
O
A
A
E
B
D
A
O
C
B
A
O
D
B
D
B
O
C
C
A
C
B
D
O
例1 已知 AB ,如图,用直尺和圆规求作这条
弧的中点.
作法: ⒈ 连结AB.
⒉ 作AB的垂直平分线 CD,交弧AB于点E.
点E就是所求弧AB的中点.
C E
B
D
变式一: 求 AB 的四等分点.
B
交点即为圆弧所在
O
圆的圆心.
1.如图,过已知⊙O内的一点A作弦,使A是该 弦的中点,然后作出弦所对的两条弧的中点.
E
N
BC就是所要求的弦 点D,E就是所要求的弦 所对的两条弧的中点.
O
FC
A
B
D
M
例2:一条排水管的截面如图所示。已知排水管的半
径OB=10,水面宽AB=16。求截面圆心O到水面的距离。
C
m
E
F
A
n
G
B
D
求 AB 的四等分点. 错在哪里?
E
C
G
M
N
P
1.作AB的垂直平分线CD
A
2.作AT、BT的垂直平分线 EF、GH
F
T
B
DH
强调:等分弧时一定要作弧所对的弦的垂
直平分线.
变式二:你能确定弧AB所在圆的圆心吗?
方法:只要在圆弧
上任意取三点,连
a
C
b
结两条弦,画这两
3.3 垂径定理(1)

9下§3.3垂径定理(1)(垂径定理)课题组一、不能遗忘的记忆(思维混乱源自记忆模糊,遗忘就意味着多用10倍的时间纠错.)1.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧;2. 垂径定理解读:(1)条件:“弦”可以是直径;(2)结论:“平分弧”既意味着平分弦所对的劣弧,也意味着平分弦所对的优弧;3. 垂径定理的三种语言:文字语言 图形语言 几何语言是直径(AB 过圆心)二、不能忽视的归纳(深度学习离不开归纳.没有归纳的学习一定是低效的,甚者是无效的.)1.回顾(补充)学习:轴对称图形:一个图形沿一条直线对折,两部分能够完全重合.2.垂径定理证明方法:构造等腰三角形,由垂直于弦得出平分弦;由圆心角相等得出弧相等.3.有关圆的常用辅助线: 连接圆心与弦一端点(半径),过圆心作弦的垂线段(弦心距),再由半径、弦心距、半弦构成直角三角形,利用勾股定理解答. 三、必须分享的智慧(没有知识的活用,没有方法的迁移,就谈不上智慧.)【典例】如图,已知圆O 的半径为mm 30,弦AB =mm 36,求点O 到AB 的距离及OAB∠的正弦值.一读:关键词:半径,弦.二联:重要结论:过圆心的垂线平分弦.重要方法:半径、半弦、弦心距构造直角三角形.三解:解: 过 圆心O 作 于M;DM AM =∴;AD AC =;BD BC =AB M CD AB ,于⊥ 18362121=⨯==∴AB AM A BO M AB OM ⊥在 中,由勾股定理得: 在 中,所以,点 到AB 的距离为mm 24,OAB ∠的正弦值为四悟:解决有关圆中相关数量问题时,常通过连接半径,作出弦心距,利用垂径定理构造直角三角形解答.四、金题核思点拨(学习抓关键,思维抓核心,学必须学的.)1. 已知圆O 的直径是m c 50,圆O 的两条平行弦cm AB 40= ,cm CD 48=,求弦AB 与CD 之间的距离.核思点拨: 弦CD AB //,但不知两弦与圆心的位置关系,所以分两种情况讨论:圆心在两弦之间或圆心在两弦同侧.再由垂径定理及勾股定理解答.答案:过点 作 于 ,则 于连接 由垂径定理得,在 中,由勾股定理得: OAM RT ∆OAM RT ∆O 1522=-=BF OB OF OBF RT ∆2421,2021====CD DE AB BF ODOB 、AB OF ⊥18,300==AM A 2422=-=AM OA OM 54302400sin ===A M A .54CD OE ⊥E O F .25,20==OB BF同理在 中,两弦在圆心同侧时,两弦距离两弦在圆心异侧时,两弦距离2. 如图,F 是圆O 直径AB 上一点,且cm AB 9=,垂直于AB 的弦cm CD 12=,垂足为F ,延长CB 到E ,使CB BE =,连接DE .求DE 的长.核思点拨: 条件中已有了弦心距OF 与半弦CF ,连半径r OC =,由垂径定理知6=CF r OF -=9,在直角三角形中用 勾股解答求出r ,从而求出 值,由三角形中位线得,答案: 连接 直径 弦在 中,由勾股定理得:cm OE OF EF 22=+=∴DOE RT ∆BF 2226)9r r =+-∴(OCF RT ∆6122121=⨯==∴CD CF ⊥AB OC722=-=DE OD OE cm OE OF EF 8=-=∴.2BF DE = CD222OC CF OF =+解得:是 的中位线132==∴BF DE CDE ∆CBBE =CFDF = 5.6=r FB ∴。
3.3 垂径定理(1)
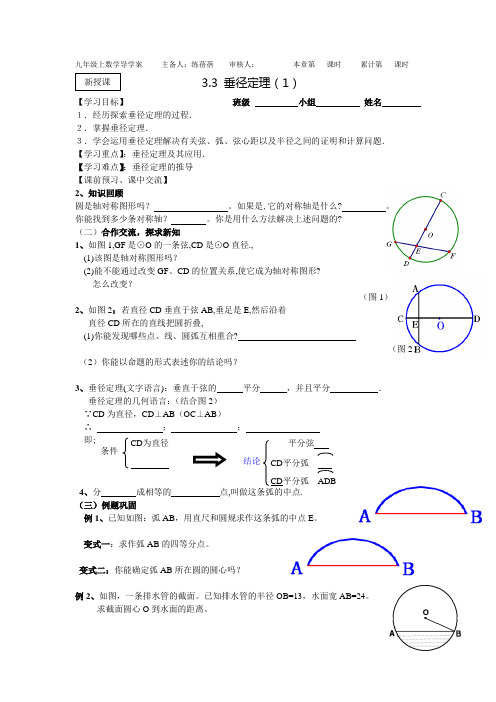
九年级上数学导学案 主备人:练蓓蓓 审核人: 本章第 课时 累计第 课时3.3 垂径定理(1)【学习目标】 班级 小组姓名 1.经历探索垂径定理的过程.2.掌握垂径定理.3.学会运用垂径定理解决有关弦、弧、弦心距以及半径之间的证明和计算问题.【学习重点】:垂径定理及其应用.【学习难点】:垂径定理的推导【课前预习、课中交流】2、知识回顾圆是轴对称图形吗? 。
如果是,它的对称轴是什么? 。
你能找到多少条对称轴? 。
你是用什么方法解决上述问题的?(二)合作交流,探求新知1、如图1,GF 是⊙O 的一条弦,CD 是⊙O 直径.,(1)该图是轴对称图形吗?(2)能不能通过改变GF 、CD 的位置关系,使它成为轴对称图形?怎么改变?(图1)2、如图2:若直径CD 垂直于弦AB,垂足是E,然后沿着直径CD 所在的直线把圆折叠,(1)你能发现哪些点、线、圆弧互相重合?(图2)(2)你能以命题的形式表述你的结论吗?3、垂径定理(文字语言):垂直于弦的 平分 ,并且平分 .垂径定理的几何语言:(结合图2)∵CD 为直径,CD ⊥AB (OC ⊥AB )∴ ; ;即; 4、分 成相等的 点,叫做这条弧的中点.(三)例题巩固例1、已知如图:弧AB ,用直尺和圆规求作这条弧的中点E 。
变式一:求作弧AB 的四等分点。
变式二:你能确定弧AB 所在圆的圆心吗?例2、如图,一条排水管的截面。
已知排水管的半径OB=13,水面宽AB=24。
求截面圆心O 到水面的距离。
新授课 条件CD 为直径 ADB平分弦结论温馨提醒:圆心到圆的一条弦的距离叫做弦心距。
那么,上图中:弦AB 的弦心距是 例3、已知:如图,线段AB 与⊙O 交于C 、D 两点,且OA=OB .求证:AC=BD .归纳小结:1.画 是圆中常见的辅助线;2.半径(r )、半弦、弦心距(d)组成的 三角形是研究与圆有关问题的主要思路, 它们之间的关系:弦长222d r AB -=.注:弦长、半径、弦心距三个量中已知两个,就可以求出第三个.【课堂检测】1.已知⊙0的半径为25,一条弦的AB 的弦心距为7,则这条弦的弦长等于 .2.如图,AB 是⊙0的中直径,CD 为弦,CD ⊥AB 于E ,则下列结论中不一定成立的是( ) A .∠COE=∠DOE B .CE=DE C .OE=BE D .BD=BC 3.过⊙O 内一点M 的最长弦长为10cm ,最短弦长为8cm ,那么OM 长为( )A .3B .6cmC . cmD .9cm4.如图,⊙O 的直径为10,弦AB 长为8,M 是弦AB 上的动点,则OM 的长的取值范围是( )A .3≤OM ≤5B .4≤OM ≤5C .3<OM<5D .4<OM<55. 已知⊙O 的半径为10,弦AB ∥CD ,AB=12,CD=16,则AB 和CD 的距离为 .6.如图,已知AB 、AC 为弦,OM ⊥AB 于点M , ON ⊥AC 于点N ,BC=4,求MN 的长.拓展提高1、已知:如图,在以O 为圆心的两个同心圆中,大圆的弦AB 交小圆于C ,D 两点。
3.3垂径定理

O
D
⌒如图,用直尺和圆规求作这条弧 例1:已知AB
的中点。
A
B
例2:如图,一条排水管的截面。已知排水管
的半径OB=10,水面宽AB=16。求截面圆心O到
水面的距离。
C 圆心到圆的一条弦的距离叫做弦心距
练习1
已知⊙O的半径为13cm,
一条弦的弦心距为5cm,求这条弦的长
C
13 5
CP=_____ CD=_____ O AP=_____
3.3
垂径定理
圆是轴对称图形吗?
●
O
圆是轴对称图形, 每一条直径所在的直线都是对称轴。
探索规律
1.任意作一个圆和这个圆的任意一条直径CD;
2.作一条和直径CD垂线的弦AB ,AB与CD相交于点E
问题:把圆沿着直径CD所 在的直线对折,你发现哪 些点、线段、圆弧重合?
C
A
E
D
O
得出结论: ⌒ ⌒ ⌒ ⌒ ①EA=EB;② AC=BC,AD=BD.
B
归纳得出:
垂径定理:垂直于弦的直径平分这条弦, 并且平分弦所对的弧. 垂径定理的几何语言
∵CD为直径,CD⊥AB(OC⊥AB) ∴ EA=EB,
⌒ ⌒ ⌒ ⌒ AC=BC,AD=BD.
A
能够重合的圆弧叫相等的圆弧 分一条弧成相等的两条弧的点,叫做 这条弧的中点 ⌒ 的中点 点C即为 AB
C E
B
A
P
D
想一想:在同一个圆中,两条 弦的长短与它们所对应的弦心
弦越长, 它所对应的弦心距越短
距之间有什么关系?
六、总结回顾
(1)圆的轴对称性; (2)垂径定理. (3)画弦心距是圆中常见的辅助线; (4)半径(r)、半弦、弦心距(d)组成的直角三角形 是研究与圆有关问题的主要思路,它们之间的关系:
浙教版数学九年级上册3.3垂径定理(共13张PPT)

复习
M
●
A
1、圆弧:圆上任意两点之间的部分
2、等弧:能够完全重合的圆弧
3、弦:连结圆上任意两点的线段
4、圆具有轴对称性
O
B
实验操作
1、取出课前准备的圆,折出这个圆的一条对称轴
2、请用折叠的方法在圆上找到两个对称点
你能发现图中有那些相等的线段和弧?为什么?
C
O
·
E
A
B
D
几何演绎
如图,理由是:
梳理
A
C
M
└
●
B
O
D
条件
由①CD是直径
②CD⊥AB
可推得
结论
③AM=BM
⌒ ⌒
④AC=BC
⌒ ⌒
⑤AD=BD
归纳小结
定理:垂直于弦的直径平分弦, 并且平分弦所对的弧.
如图∵ CD是直径,
CD⊥AB,
B
∴AM = BM,
C
A
M└
O
●
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
D
分一条弧成相等的两条弧的点,叫做这条弧的中点.
问题一:
⌒
例1、已知AB如图,用直尺和圆规求作这条弧的中点.
E
⌒
分析:要平分AB,只要画垂
直于弦AB的直径.而这条直径应在弦A源自的垂直平分线上.A
作法:
1. 连结AB;
⌒
2. 作AB的垂直平分线CD,交AB与点E;
⌒
∴点E就是所求AB的中点.
B
问题二:
例2:如图已知在⊙ O 中 弦AB=16,半径0B=10,
连接OA,OB, 则OA=OB.
《垂径定理(1)》教学案

3.3 垂径定理(1)教学案教学目标知识目标:1.理解圆是轴对称图形,每一条直径所在的直线都是对称轴.2.掌握圆的性质(垂径定理),并会用它解决有关弦、弧、弦心距及半径之间关系的证明和计算.能力目标:经历折纸、画图、归纳等过程,培养学生的探索能力和应用能力.情感目标:通过合作学习,探索圆的性质;让学生亲身体验、直观感知,并操作确认,激发学生自主学习和应用数学的意识.教学重点难点重点:探索圆的轴对称性和圆的性质.难点:用圆的轴对称性推导出圆的性质及其应用.课堂教与学互动设计【创设情境,引入新课】复习提问:(1)什么是轴对称图形?(2)正三角形是轴对称性图形吗?有几条对称轴?(3)圆是否为轴对称图形?如果是,它的对称轴是什么?•你能找到多少条对称轴?──引入新课【合作交流,探究新知】一、自主探索1.在透明纸上任意作一个圆和这个圆的任意一条直径,•然后沿着直径所在的直线把纸折叠,你发现了什么?2.结论:圆是_________图形,_________的直线都是对称轴.二、合作学习1.在圆形纸片(如图所示)上任意画一条直径CD,然后在CD上任意取一点E,过E画弦AB⊥CD于点E,把圆形纸片沿直径对折,观察直径CD两侧,你发现哪些点、线互相重合?有哪些圆弧相等?2.请你用命题的形式表达你的结论.3.请你对上述命题写出已知、求证,并给出证明.4.圆的性质(垂径定理):垂直于弦的直径平分这条弦且平分弦所对的弧.三、概括性质1.直径垂直于弦..⎧⇒⎨⎩直径平分弦直径平分弦所对的弧例如:CD是直径,AB⊥CD,EA=EB,CA CB=,DA DB=.2.分一条弧成相等的两条弧的点,叫做这条弧的中点.例如,上图中,•点C•是AB的中点,D是ADB的中点.【例题解析,当堂练习】例1 (课本例1)已知AB(如图),用直尺和圆规求作这条弧的中点.练一练如图,同心圆O中,大圆的弦AB与小圆交于C,D两点,判断线段AC与BD的大小关系,并说明理由.例2 (课本例2)一根排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,求截面圆心O 到水面的距离OC .想一想在同一个圆中,两条弦的长短与它们所对应的弦心距之间有什么关系?练一练 在直径为20cm 的球形油槽内装入一些油后,截面如下图所示,•如果油面宽是16cm ,求油槽中油的最大深度.课外同步训练【轻松过关】1.⊙O 的弦AB 的长为16cm ,弦AB 的弦心距为6cm ,则⊙O 的半径为( )A .6cmB .8cmC .10cmD .12cm2.圆是轴对称图形,它的对称轴有( )A .1条B .2条C .4条D .无数条3.如图3-3-6,在⊙O 中,直径MN ⊥AB ,垂足为C ,则下列结论中错误的是( )A .AC=BCB .AN BN =C .AM BM =D .OC=CN图3-3-6 图3-3-7 图3-3-84.如图3-3-7,AB,CD是⊙O的两条直径,∠BOC≠∠AOC,则图中相等的弧共有()A.2对B.4对C.6对D.8对5.⊙O的半径为6cm,垂直平分半径的弦长是_______cm.6.如图3-3-8,已知AB是⊙O的弦,P是AB上一点,若AB=10cm,PB=4cm,OP=5cm,则⊙O的半径OB=_______cm.7.如图3-3-9,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD于点E,请你写出一个你认为正确的结论_________.图3-3-9 图3-3-10 图3-3-11 8.如图3-3-10,OA为⊙O的半径,弦CB⊥OA于点P,已知OC=5,OP=3,则弦CB•的长为________.9.如图3-3-11,CD为圆O的直径,弦AB⊥CD,P为垂足,•AB=•8cm,•PD=•2cm,则CP=______cm.10.如图3-3-12所示,在直径为52cm的圆柱形油桶内装入一些油后,•如果油的最大深度为16cm,那么油面宽度AB是_______cm.图3-3-12。
3.3 垂径定理 教案(表格式)2023-2024学年浙教版九年级数学上册
教学设计课程基本信息学科数学年级九年级学期秋季课题 3.3垂径定理(第一课时)教科书书名:《义务教育教科书数学(九年级上册)》出版社:浙江教育出版社教学目标1. 经历探索垂径定理的过程.2. 探索并掌握垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.3. 会运用垂径定理解决一些简单的几何问题.教学内容教学重点:垂径定理教学难点:垂径定理的推导过程以及垂径定理的灵活运用教学过程一:创设情境引入新课问题1:如图,剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了什么?由此你能得到什么结论?我们发现在折叠的过程中,直径两侧的部分会完全重合,因此我们得到结论:圆是轴对称图形任何一条直径所在直线都是它的对称轴.问题2:如图,在⊙O中任意作一条弦AB,观察下面的图形,它还是轴对称图形吗,若是,你能作出它的对称轴吗?二:师生互动共创新知已知:如图,CD是⊙O的直径,CD⊥AB,求证:AE=BE,AĈ=BĈ,AD̂=BD̂.分析:利用半径来构造等腰三角形来证明AE=BE;弧等可以利用同圆或等圆中两弧的端点重合来证明.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.几何语言:∵CD是直径,CD⊥AB,∴AE=BE,AĈ=BĈ,AD̂=BD̂. 三:应用新知层层深入B OACD下列图形是否适合用垂径定理呢?例1 已知AB̂,用直尺和圆规作这条弧的中点 分析:要平分弧,找到这条弧的中点,让我们联想到了垂径定理的 基本图形,所以第一步我们先连结AB ,然后再画出垂直弦AB 的过圆心的一条直线即可,所以第二步,作AB 的垂直平分线CD , 交弧AB 于点E.例2 一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,求截面圆心O 到水面的距离.分析:为求O 到AB 的距离,我们先过点O 作OC ⊥AB ,即求OC的长度,观察图形发现OC 在直角三角形OBC 中,其中半径 OB=10,由于OC ⊥AB ,由垂径定理可得BC 等于AB 的一半等于8, 那么根据勾股定理即可得到OC 的长度.变式:一条排水管的截面如图所示。
3.3垂径定理
O ·
A
E
D
B
小结:
A
解决有关弦的问题,常用辅助线:
M B A C C A D B N D B
. O
连接半径
O E
.
.O
过圆心作 弦的垂线
垂直于弦的直径
为应用垂径定理创造条件
常用辅助线:
垂直于弦的直径
学生练习
已知:AB是⊙O直径,CD 是弦,AE⊥CD,BF⊥CD 求证:EC=DF A E C D O
A
●
O
D
小于半圆的弧叫做劣弧,如记作 ⌒ AB(用 两个字母).
C
⌒ 大于半圆的弧叫做优弧,如记作 AmB (用三个字母).
猜想探索
如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M。 (1)该图是轴对称图形吗?如果是,其对称轴是什么? (2)你能图中有哪些等量关系?说一说你的理由。
垂径定理的逆定理
如图,AB是⊙O 的弦(不是直径),作一条平分AB的直 径CD,交AB于点M.
(1)下图是轴对称图形吗?如果是,其对称轴是什么? (2)图中有哪些等量关系?说一说你的理由. C A
●
B
O
由
M
●
① CD是直径 ② AM=BM
可推得
③CD⊥AB, ⌒ ⌒ ④AC=BC, ⌒ ⌒ ⑤AD=BD.
最短的弦等于_________。
M
.
O
P N
A
B
双基训练 1. 如图,将半径为2cm的圆形纸片折叠后,圆弧 恰好经过圆心,则折痕AB的长为( C ) A.2cm B. 3 cm C. 2 3cm D. 2 5 cm
O A
B
2.已知点P是半径为5的⊙O内 的一定点,且OP=4,则过P 点的所有弦中,弦长可能取 的整数值为( C )
3.3 垂径定理 课件 2023-2024学年 北师大版数学九年级下册
*3.3 垂径定理
续表
(1)定理中的“垂径”可以是直径、半径或过圆心的直线(线段),其 本质是“过圆心”; 特别提醒 (2)“平分弦所对的两条弧”是指既平分弦所对的优弧(如图中的
),又平分弦所对的劣弧(如图中的 )
-2-
*3.3 垂径定理
2. 垂径定理的推论
文字描述 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧 如图,直径 CD 与非直径的弦 AB
的是 ( )
A. CM=DM B.
C. ∠ACD=∠ADC D. OM=MB
(第 1 题图)
(第 2 题图)
2. 如图所示,⊙O 的半径为 13,弦 AB 的长度是 24,ON⊥AB,垂足为 N,
则 ON= ( )
A. 5
B. 7
C. 9
D. 11
-1-
*3.3 垂径定理
3.(教材 P76,习题 T2 变式)如图,AE 是⊙O 的直径,半径 OD 垂直于 弦 AB,垂足为 C,AB=8 cm,CD=2 cm,求 BE 的长.
∴AN= AB=12, 在 Rt△AON 中, ∵AO=13,∴ON=
=5.
3. 解:∵ 半径 OD 垂直于弦 AB,垂足为 C, AB=8 cm,∴AC= AB=4 cm,
设 CO=x cm,则 AO=DO=(x+2)cm,在 Rt△AOC 中,AO2=CO2+AC2, ∴(x+2)2=x2+42,解得 x=3,即 CO=3 cm. ∵AO=EO,AC=CB,OC 为△ABE 的中位线,∴BE=2CO=6 cm. 4. D 提示:一条直线经过圆心,平分弦所对的劣弧,根据垂径定理及其推论可 知,它垂直平分这条弦,并且平分弦所对的优弧. 5. 120 提示:∵ 弦 AC 与半径 OB 互相平分,∴OA=AB,∵OA=OB,∴△OAB 是 等边三角形,∴∠AOB=60°,∴∠AOC=2∠AOB=120°.
3.3垂径定理1
当AB也是直径时 结论仍然成立。
垂径定理本质上就是等 腰三角形的三线合一
垂径定理:垂直于弦的直径平分这条弦,并且平分弦 所对的弧。 证明:连结OA、OB,则OA=OB 在等腰三角形OAB中,OC⊥AB,得EA=EB(为什么?)。 所以把图沿直径CD对折时,因为∠AEO=∠BEO=Rt∠, 所以射线EA与射线EB重合,从而点A与点B重合。 这样弧AC与弧BC,弧AD与弧BD分别重合,所以弧AC与 弧BC,弧AD与弧BD分别相等, 记作弧AC=弧BC,弧AD=弧BD。 分一条弧成相等两部分的点, 叫做这条弧的中点。 C是弧AB的中点;D是弧ADB 的中点。
提高练习
2,书本P78作业题4,5,6
区分“弦AB垂直平分半径OC” 与“半径OC垂直平分弦AB”
第6题:方法一:用轴对称性证明;方法二:弧也可以 像线段那样加减(必须在同圆或等圆中)。
补充练习
3,点A在⊙O内,过点A作一条弦BC,使得BC是所有过 点A的弦中最长的。 最长:弦BC过圆心O时(直径) 那你知道过A点的弦中最短的在哪个位置吗? 最短:弦BC⊥OA时
你知道四者当中至少知道 几个量才能求出剩下的量?
课堂小结
1,你还记得垂径定理吗? 垂直于弦的直径平分这条弦,并且平分弦所对的弧。 2,垂径定理的两个用途? 几何证明、代数计算 3,弦长(或半弦长)、弦心距、半径(或直径)、弓高(矢 高) 他们之间有怎样的数量关系? 和差倍分、勾股定理
基础练习
1,书本P77课内练习1,2 书本P78作业题1,2,3
如图, ⊙O中,直径DE⊥弦AB,垂足为C点,那么其中 AB长度叫做弦长;OC长度叫做______;OB叫做_____; CD长度叫做弓形ADB的高(EC长度叫做弓形AEB的高) 弦长、弦心距、半径、弓高(矢 高)四者之间有着密切的联系。 你能找出他们之间的关系吗? 1)弦心距OC+弓高CD=半径 弓高EC﹣弦心距OC=半径 2)AC=BC=弦长AB的一半 3)勾股定理 OB2 BC2 OC 2 与圆有关的计算问题,只要是 围绕着这四者间的关系展开的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
OC OB BC 10 8 6
2 2 2 2
8
C
10 8
答:截面圆心O到水面的距离为6.
D
圆心到圆的一条弦的距离叫做弦心距.
例如,上图中,OC的长就是弦AB的弦心距.
师生共同总结:
1.本节课主要内容:(1)圆的轴对称性;(2)垂径定理.
2.垂径定理的应用:(1)作图;(2)计算和证明.
C A
EBOຫໍສະໝຸດ D2.请你用命题的形式表述你的结论. 垂直于弦的直径平分这条弦, 并且平分弦所对的弧.
垂直于弦的直径平分这条弦,并且平分弦所对的弧.
3.请你对上述命题写出已知,求证,并给出证明. 解 已知:如图,CD是⊙O的直径,AB是⊙O的一 条弦,CD⊥AB,且交AB于点E. ⌒ ⌒ ⌒ ⌒ 求证: EA=EB, AC= BC, AD=BD.
A D E B C
⌒
1.如图,过已知⊙O内的一点A作弦,使A是该弦 的中点,然后作出弦所对的两条弧的中点. E
BC就是所要求的弦 点D,E就是所要求的弦 所对的两条弧的中点.
O
C
A
B
D
例2:一条排水管的截面如图所示。已知排水管的半
径OB=10,水面宽AB=16。求截面圆心O到水面的距离。
想一想:排水管中水最深多少? 解:作OC⊥AB于C, 由垂径定理得: AC=BC=1/2AB=0.5×16=8. 由勾股定理得:
证明: 如果把⊙O沿着直径CD 对折,那么被CD分成的两个 半圆互相重合. ∵∠OEA=∠OEB=Rt∠, ∴线段EA与线段EB重合. ∴点A与点B重合,弧AC和弧BC重合,
A C D
E
B
O
思考:你能利用等腰 三角形的性质,说明
弧AD和弧BD重合. ⌒ ⌒ ⌒ OC平分AB吗? ⌒ ∴ EA=EB, AC= BC, AD=BD.
4.圆的性质(垂径定理)
垂直于弦的直径平分这条弦,
并且平分弦所对的弧.
C
A D
O A D E B
B
A
O D C B
O
C
A
O C B
例1 已知弧AB,如图,用直尺和圆规求作这条弧 的中点.(先介绍弧中点的概念) 分一条弧成相等的两条弧的点,叫做这条弧的中点. ⌒ 分析:要平分AB,只要画垂直于弦AB的直径.而这 条直径应在弦AB的垂直平分线上.因此画AB的 ⌒ 垂直平分线就能把AB平分. 作法: ⒈ 连结AB. ⒉ 作AB的垂直平分线 CD,交弧AB于点E. 点E就是所求弧AB的中点.
3.解题的主要方法: (1)画弦心距和半径是圆中常见的辅助线; (2)半径(r)、半弦、弦心距(d)组成的直角三角形 是研究与圆有关问题的主要思路,它们之间的关系:
弦长AB 2 r 2 d 2 .
创设情境,引入新课
复习提问: (1)什么是轴对称图形
如果一个图形沿着一条直线对折,两侧的图形能 完全重合,这个图形就是轴对称图形。
(2)圆是否为轴对称图形?如果是,它的对 称轴是什么?你能找到多少条对称轴?
合作交流,探究新知
一自主探究 在白纸上任意作一个圆和这个圆的任意一条直径CD, 然后沿着直径所在的直线把纸折叠,你发现了什么?
C
O
D
结论:
圆是轴对称图形,每一条直径所在的直线都是对称轴。 强调:
(1)圆的对称轴是直线,不能说每一条直径都是圆的对称轴. (2)圆的对称轴有无数条.
判断:任意一条直径都是圆的对称轴(
X)
二
合作学习
1.在刚才操作的基础上,再作一条和直径CD垂直的弦 AB,AB与CD相交于点E,然后沿着直径CD所在的直线把纸 折叠,你发现哪些点、线互相重合?如果把能够重合的圆 弧叫做相等的圆弧(等弧),有哪些圆弧相等? 解:点A与点B重合,AE与BE重合, ⌒ ⌒ ⌒ ⌒ AC=BC,AD=BD.
