大学物理 电动势的计算
合集下载
大学物理动生电动势和感生电动势
S
dt
S不变
dB Ek dl dS L S dt
dB dS S dt
揭示了电场和磁场是相互联系的。
10 - 2 动生电动势和感生电动势
第十三章电磁感应
dB Ek dl dS L S dt
dl Rd
2
b
d
vB dl
R
v
B
vBR
2
cos d
方向：a
vB2 R
b
a
10 - 2 动生电动势和感生电动势
第十三章电磁感应
二
感生电动势（阅读）
1、感生电动势 由于磁场发生变化 而激发的电动势
G S N
是什么力使电荷运 动而在电路中产生 电流的呢？？？
R
10 - 2 动生电动势和感生电动势
第十三章电磁感应
例5. 匀强磁场B，导体棒OP绕OZ轴旋转，角 速度 , OP=b， 为已知 OZ轴∥ B 。求PO两端的电势差？
思路：d ( v B ) dl
vB cos dl
rB sin d l
R
B
解：方法一 作辅助线，形成闭合回路
i 0 半圆 ab 2 RBv
方向：a
a
b
10 - 2 动生电动势和感生电动势
第十三章电磁感应
有一半圆形金属导线在匀强磁场中作切割磁
力线运动。已知： v , B , R.
求：动生电动势。 解：方法二
d ( v B ) dl 0 vB sin 90 dl cos
(D) 两环中感应电动势相等。
dt
S不变
dB Ek dl dS L S dt
dB dS S dt
揭示了电场和磁场是相互联系的。
10 - 2 动生电动势和感生电动势
第十三章电磁感应
dB Ek dl dS L S dt
dl Rd
2
b
d
vB dl
R
v
B
vBR
2
cos d
方向：a
vB2 R
b
a
10 - 2 动生电动势和感生电动势
第十三章电磁感应
二
感生电动势（阅读）
1、感生电动势 由于磁场发生变化 而激发的电动势
G S N
是什么力使电荷运 动而在电路中产生 电流的呢？？？
R
10 - 2 动生电动势和感生电动势
第十三章电磁感应
例5. 匀强磁场B，导体棒OP绕OZ轴旋转，角 速度 , OP=b， 为已知 OZ轴∥ B 。求PO两端的电势差？
思路：d ( v B ) dl
vB cos dl
rB sin d l
R
B
解：方法一 作辅助线，形成闭合回路
i 0 半圆 ab 2 RBv
方向：a
a
b
10 - 2 动生电动势和感生电动势
第十三章电磁感应
有一半圆形金属导线在匀强磁场中作切割磁
力线运动。已知： v , B , R.
求：动生电动势。 解：方法二
d ( v B ) dl 0 vB sin 90 dl cos
(D) 两环中感应电动势相等。
电动势与内阻的公式
电动势与内阻的公式主要有两种：
不计内阻的情况下，电动势的公式为E=IR总，其中E为电动势，I为外路电流，R总为总电阻。
考虑内阻的情况下，电动势的公式为E=U内+U外=I(r+R)，或者E=I(R+r)，其中r为内阻，R为外电阻，U内为内电压，U外为外电压。
在测电源电动势和内电阻的实验中，通常使用闭合电路欧姆定律来测量。
根据闭合电路欧姆定律，电动势E等于电源两端的电压U加上电源内阻r上的电压降Ir，即E=U+Ir。
通过改变外电阻R，测量出对应的路端电压U和电流I，可以用公式法或图像法求出电源的电动势E和内电阻r。
需要注意的是，电动势E是描述电源将其他形式的能量转化为电能的本领大小的物理量，其大小等于非静电力把单位正电荷从电源的负极，经过电源内部移送到正极时所做的功。
而内阻r则是电源内部的电阻，它反映了电源将电能转化为其他形式能量的能力大小。
因此，电动势和内阻都是描述电源性质的重要物理量。
大学物理Ⅱ2.1 动生电动势
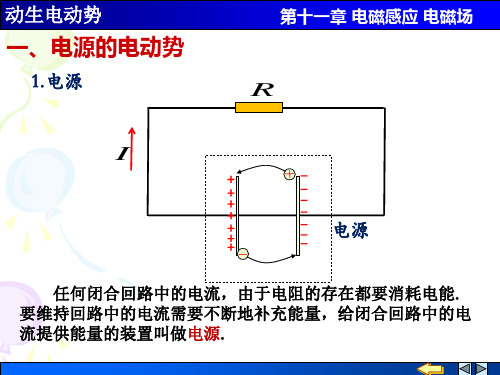
磁力线运动。已知： v, B, R.
求：动生电动势。
dl Rd
vB
解：方法一
d
(
v
B
)
dl
vBdl cos
2
vBR cosd 2 vB2R 方向：a b
b
dl
d
v
R
B
a
动生电动势
第十一章 电磁感应 电磁场
解：方法二
b
作辅助线，形成闭合回路
i 0
v
半圆
ab
2RBv
动生电动势
第十一章 电磁感应 电磁场
1、在磁场中运动的导线内的感应电动势
由于导体运动而产生的感应电动势，称为动生
电动势。
dΦ B d S Bl d x
i
dΦ dt
Bl d x
dt
D
A
v
B l
C B dx
Blv
动生电动势
第十一章 电磁感应 电磁场
解
i
b (v B) dl
a
b
vBdl
a
B
vB(ab) 2vB R2 r2
O
v
R
r dl
b
a
动生电动势
第十一章 电磁感应 电磁场
2．在磁场中转动的线圈内的感应电动势
设矩形线圈ABCD
o
的匝数为N ,面积为S， 使这线圈在匀强磁场中
绕磁直的间固感。夹B，定应当角的 强 为与时轴 度 零t 之，t线 ，与间0经OenO与的过B轴转夹时之eB垂动角n O间O，
Bv sin dl
0L Bv sin dl
BvLsin
dl
v
L
B
动生电动势 典型结论
大学物理-第12章--电磁感应
∴取以 r 为半径的圆周为绕行回路L ，绕行方向为逆时针,面元法线如图。
× × × ×
× ×××
r n ×L × × × ×
× × ××× × R
×××××
×
B
×× ×× ×× ××
当r < R
时： L E感 dl
S
B
dS
t
等式左边 L E感 dl L E感dl cos 00
× × × ×
导线内每个自由电子
受到的洛仑兹力为：
fm e(v B)
非静电力
?++ + ++
B
v
fm
在导线内部产生的静电场方向
ab
E
a
++ + ++
电子 受的静电力
fe
fe eE
平衡时： fe fm
此时电荷积累停止，
fm
ab 两端形成稳定的电势差。 b
★ 洛仑兹力是产生动生电动势的根本原因.
B
v
2、动生电动势的表达式
S 1 hL 2
磁通
m
1 hLB 2
B
t
0
o B h
C D
i
dm dt
1 hL dB 1 hL B 2 dt 2 t
L
讨论 只有CD导体存在时，
电动势的方向由C指向D
加圆弧连成闭合回路，
由楞次定理知：感生电流的
方向是逆时针方向……..
1 B hL
1 2 t
B SOCD t
？
铁芯
磁场 B
线圈
电 子束
环形 真空室
五、感生电场计算举例
例 12-5. 半径为R的长直螺线管内的磁场，以dB/dt 速
× × × ×
× ×××
r n ×L × × × ×
× × ××× × R
×××××
×
B
×× ×× ×× ××
当r < R
时： L E感 dl
S
B
dS
t
等式左边 L E感 dl L E感dl cos 00
× × × ×
导线内每个自由电子
受到的洛仑兹力为：
fm e(v B)
非静电力
?++ + ++
B
v
fm
在导线内部产生的静电场方向
ab
E
a
++ + ++
电子 受的静电力
fe
fe eE
平衡时： fe fm
此时电荷积累停止，
fm
ab 两端形成稳定的电势差。 b
★ 洛仑兹力是产生动生电动势的根本原因.
B
v
2、动生电动势的表达式
S 1 hL 2
磁通
m
1 hLB 2
B
t
0
o B h
C D
i
dm dt
1 hL dB 1 hL B 2 dt 2 t
L
讨论 只有CD导体存在时，
电动势的方向由C指向D
加圆弧连成闭合回路，
由楞次定理知：感生电流的
方向是逆时针方向……..
1 B hL
1 2 t
B SOCD t
？
铁芯
磁场 B
线圈
电 子束
环形 真空室
五、感生电场计算举例
例 12-5. 半径为R的长直螺线管内的磁场，以dB/dt 速
大学物理中的电磁感应电动势和磁感应强度的计算
大学物理中的电磁感应电动势和磁感应强度的计算电磁感应中的电动势和磁感应强度计算1. 介绍电磁感应在大学物理中，电磁感应是一个重要的概念。
它指的是通过磁场的变化产生电动势的现象。
根据法拉第电磁感应定律，导线中的电动势等于磁通量的变化率乘以导线的匝数。
2. 电动势的计算公式根据法拉第电磁感应定律，一个导体中的电动势（ξ）可以用以下公式计算：ξ = -dΦ/dt其中ξ表示电动势，dΦ表示磁通量的变化，dt表示时间的变化。
负号表示电动势的方向与磁通量变化的方向相反。
3. 磁感应强度的计算公式磁感应强度（B）是一个磁场对空间中各点带电粒子或电流的作用力大小的量度。
根据安培环路定律，一个闭合回路的磁通量等于该回路内的电流与回路面积的乘积。
B = Φ/S其中B表示磁感应强度，Φ表示通过闭合回路的磁通量，S表示闭合回路的面积。
4. 电动势和磁感应强度的实际应用在实际应用中，电动势和磁感应强度的计算非常重要。
它们可以用来解释各种电磁现象，如发电机的原理、感应电动势和变压器的工作原理等。
5. 电动势和磁感应强度的计算例子举个例子来说明电动势和磁感应强度的计算。
假设有一个导线环路，通过它的磁通量随时间变化。
我们可以根据电动势的计算公式来求解这个导线环路中的电动势。
另外，如果我们已知一个闭合回路内的电流和回路面积，我们可以根据磁感应强度的计算公式来求解磁感应强度。
6. 结论电磁感应是大学物理中一个重要的概念，涉及电动势和磁感应强度的计算。
电动势可以通过磁通量的变化来计算，而磁感应强度可以通过磁通量与闭合回路面积的比值来计算。
它们在实际应用中具有广泛的意义，可以用来解释各种电磁现象。
在学习和应用中，遵循正确的计算公式和方法是非常重要的。
大学物理电动势的计算
磁场平行于ab边，bc的长度为l．当金属框架绕ab边以匀角
速度 转动时，abc回路中的感应电动势 和a、c两点间的
电势差Ua – Uc为
(A) 0
Ua
–
=
1 2
Bl
2
(B)
0，
Ua
–
Uc
=
1 2
Bl
2
B
b
l c
(C)
Bl 2
，Ua
–
Uc
1
=
2
Bl 2
(D)
Bl，2 Ua
–
Uc
=
1 2
Bl 2
(A) 线圈中无感应电流． (B) 线圈中感应电流为顺时针方向． (C) 线圈中感应电流为逆时针方向． (D) 线圈中感应电流方向不确定．
I
I
[ B]
第13章 电磁感应
13
§13-2 电动势的计算
8.用导线制成一半径为r =10 cm的闭合圆形线圈，其电阻R =10Ω ，均匀磁场垂直于线圈平面．欲使电路中有一稳定的感 应电流i = 0.01 A，B的变化率应为dB /dt =___3_._1_8__T_/s____．
的函数关系？(从线圈刚进入磁场时刻开始计时，I以顺时针方向
为正)
v
B
I (A)
O
I (C)
O
I (B)
t
O
I
t
O
(D)
t
t
第13章 电磁感应
[C]
12
§13-2 电动势的计算
7.两根无限长平行直导线载有大小相等方向相反的电流I，并 各以dI /dt的变化率增长，一矩形线圈位于导线平面内(如图)， 则：
大学物理9-2 电源电动势 全电路欧姆定律
第九章
恒定电流的磁场
1I 2 I 1.5 0.2 0.30(W )
可见因第二个电池内阻太高，虽其电动势为1.5V，与第 一个电池串联供电时，其路端电压是负的，电池的总功率 小于其内阻的损耗功率。所以，在实际中不能将一节新电 池和一节旧电池串联使用。
9 – 2 电源电动势
第九章
E Ek 0
电源的路端电压
U
(电源内)
E dl
（ 电源内 ）
E k dBiblioteka 9 – 2 电源电动势 2 电源供电、充电 电源内欧姆定律的微分形式
第九章
恒定电流的磁场
j (E Ek )
得
1 E j Ek
9 – 2 电源电动势 电源电动势的图示符号
第九章
恒定电流的磁场
9 – 2 电源电动势 *三 电源的路端电压
第九章
恒定电流的磁场
电源的路端电压，即电源两电极之间的电压。它等于把 单位正电荷从正极移到负极静电场力所做的功，即
U U U
这里积分路径是任意的。 1 电源开路
E dl
* C
R
* D
ldU l E d l 0
A *
I E Ri * B * 电源
U AC UCD U DB U BE U EA 0
9 – 2 电源电动势
第九章 * C
恒定电流的磁场 * D I
U AC U DB 0
IR IRi 0
R
U 2 I 2 Ri
解得
U1 U 2 2.30 1.98 Ri 0.01() I1 I 2 20 12
《大学物理》6.2动生电动势感生电动势解读
k
b
B B 1 2 dS 解: bc R S t t 2
B 0 t
× ×
O × × × ×
uc ub
a
× ×
上页
b E c
下页
四、涡电流
产生原因： 大块的金属导体处在变化的磁场中时，通过金属 块的磁通量发生变化，从而产生感应电动势，在 金属内部形成电流，称为涡电流。 涡电流特点：
A
G
E
B
。。
下页
如何度量这种本领？ ε----电动势
上页
电动势： 电源把单位正电荷经内电路从 负极移到正极的过程中，非静 电力Fk所作的功 从场的观点： 非静电力对应非静电场
A非 q
q
E0
Fk qEk A非 Fk dl q Ek dl Ek dl
d 1.热效应： i dt
I
i
R
I(ω)
Q I 2 Rt 2
表明： 交流电频率越高发热越多——感应加 热原理
I(ω)
I(ω) I(ω)
I’
2.磁效应： 阻尼摆
上页 下页
小结：
动生电动势：磁场分布不变, 回路或导线在磁场中运动而引起的感应电动
势 感生电动势：导体回路不动,磁场随时间发生变化而引起的感应电动势
静电场
静止电荷
涡旋电场
变化磁场
有源场
无源场
上页 下页
感生电动势的计算 法拉第电磁感应定律
i
L
d d Ek dl
dt
dt
S B d S
因为回路固定不动，磁通量的变化仅来自磁场的变化
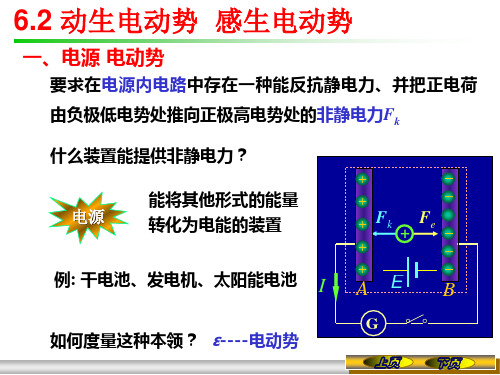
b
B B 1 2 dS 解: bc R S t t 2
B 0 t
× ×
O × × × ×
uc ub
a
× ×
上页
b E c
下页
四、涡电流
产生原因： 大块的金属导体处在变化的磁场中时，通过金属 块的磁通量发生变化，从而产生感应电动势，在 金属内部形成电流，称为涡电流。 涡电流特点：
A
G
E
B
。。
下页
如何度量这种本领？ ε----电动势
上页
电动势： 电源把单位正电荷经内电路从 负极移到正极的过程中，非静 电力Fk所作的功 从场的观点： 非静电力对应非静电场
A非 q
q
E0
Fk qEk A非 Fk dl q Ek dl Ek dl
d 1.热效应： i dt
I
i
R
I(ω)
Q I 2 Rt 2
表明： 交流电频率越高发热越多——感应加 热原理
I(ω)
I(ω) I(ω)
I’
2.磁效应： 阻尼摆
上页 下页
小结：
动生电动势：磁场分布不变, 回路或导线在磁场中运动而引起的感应电动
势 感生电动势：导体回路不动,磁场随时间发生变化而引起的感应电动势
静电场
静止电荷
涡旋电场
变化磁场
有源场
无源场
上页 下页
感生电动势的计算 法拉第电磁感应定律
i
L
d d Ek dl
dt
dt
S B d S
因为回路固定不动，磁通量的变化仅来自磁场的变化
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 2
Bl 2
B
b
l c
a
［B ］
第13章 电磁感应
10
§13-2 电动势的计算
4、一矩形线框长为a宽为b，置于均匀磁场中，线框绕OO′轴，
以匀角速度旋转(如图所示)．设t =0时，线框平面处于纸面内，
则任一时刻感应电动势的大小为
(A) 2abB | cos t |． (B) abB
5
§13-2 电动势的计算
1.载有电流的I长直导线附近，放一导体半圆环MeN与长直导线共
面，且端点MN的连线与长直导线垂直．半圆环的半径为b，环心
O与导线相距a．设半圆环以速度 v平行导线平移，求半圆环内
感应电动势的大小和方向以及MN两端的电压UM - UN ．
v
e
IM
b O
N
a
第13章 电磁感应
(C)
1abBcos t
2
(D) abB | cos t |．(E) abB | sin t |． ［ D ］
O
b
B
a
O′
第13章 电磁感应
11
§13-2 电动势的计算 5.
ADCBA
ADCBA
第13章 电磁感应
12
§13-2 电动势的计算
6.如图所示，一矩形金属线框，以速度 v从无场空间进入一均
匀磁场中，然后又从磁场中出来，到无场空间中．不计线圈的
自感，下面哪一条图线正确地表示了线圈中的感应电流对时间
的函数关系？(从线圈刚进入磁场时刻开始计时，I以顺时针方向
为正)
v
B
I
I
(A )
(B )
O
t
O
I
t
I
O
(Байду номын сангаас )
(D )
t
O
t
第13章 电磁感应
[C]
13
§13-2 电动势的计算
7.两根无限长平行直导线载有大小相等方向相反的电流I，并 各以dI /dt的变化率增长，一矩形线圈位于导线平面内(如图)， 则：
§13-2 电动势的计算
主要内容： 动生、感生电动势的计算 重 点： 动生、感生电动势的计算 难 点： 感生电场
第13章 电磁感应
1
§13-2 电动势的计算
第13章 电磁感应
2
§13-2 电动势的计算
第13章 电磁感应
3
§13-2 电动势的计算
第13章 电磁感应
4
§13-2 电动势的计算
第13章 电磁感应
第13章 电磁感应
15
6
§13-2 电动势的计算
第13章 电磁感应
7
§13-2 电动势的计算 2. 如图所示，一长直导线通有电流I，其旁共面地放置一匀质 金属梯形线框abcda，已知：da =ab =bc =L，两斜边与下底边 夹角均为60°，d点与导线相距l．今线框从静止开始自由下 落H高度，且保持线框平面与长直导线始终共面，求：
磁场平行于ab边，bc的长度为l．当金属框架绕ab边以匀角
速度 转动时，abc回路中的感应电动势 和a、c两点间的
电势差Ua – Uc为
(A) 0
Ua
–
Uc
=
1 2
Bl 2
(B)
0 ，
Ua
–
Uc
=
1 2
Bl
2
(C)
Bl2
，Ua
–
Uc
1
=
2
Bl2
(D)
Bl，2 Ua – Uc =
(1) 下落高度为H的瞬间， 线框中的感应电流为多少？
(2) 该瞬时线框中电势最 高处与电势最低处之间的电 势差为多少？
ab
l 60° c d
I H
第13章 电磁感应
8
§13-2 电动势的计算
第13章 电磁感应
9
§13-2 电动势的计算
3、 如图所示，直角三角形金属框架abc放在均匀磁场 B 中，
(A) 线圈中无感应电流． (B) 线圈中感应电流为顺时针方向． (C) 线圈中感应电流为逆时针方向． (D) 线圈中感应电流方向不确定．
I
I
[ B]
第13章 电磁感应
14
§13-2 电动势的计算
8.用导线制成一半径为r =10 cm的闭合圆形线圈，其电阻R =10Ω ，均匀磁场垂直于线圈平面．欲使电路中有一稳定的感 应电流i = 0.01 A，B的变化率应为dB /dt =___3_._1_8__T_/s____．