《大学物理》动生电动势 (1)
合集下载
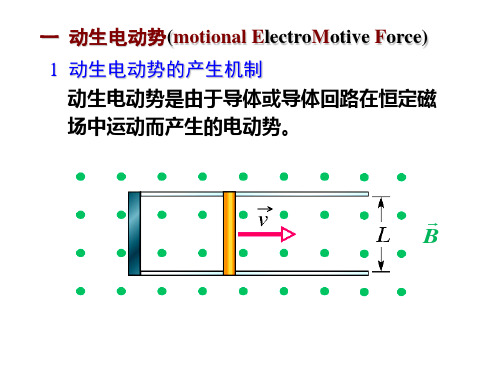
大学物理——动生电动势
v
I a
x L
dx
B
x
v和 B 的夹角： 1 / 2, V B 与 dx 的夹 2
角： 导体元所产生的动生电动势方向沿 x轴负向，
0 I B 导体元处的磁场 B 为： 2 x
d i vBdx sin cos vBdx 大小为： 2
代入
Ek dl 得: (v B) dl
大小：
1为 v 与 B 的夹角
vBdl sin 1 cos 2
2为 v B 与 dl
的夹角。
方向：电动势方向从负极到正极。 以上结论普遍成立。
如果整个回路都在磁场中运动，则在回路中产生的总 的电动势为： (v B) dl
E感
R dB 2 dt
dB 2 E 感 2r R dt R 2 dB 1 所以 E 感 2r dt r
o
R
r
17
E感分布曲线
例2：圆形均匀分布的磁场半径为 R，磁场随时间均匀
dB k ，在磁场中放置一长为 L 的导体棒，求 dt 棒中的感生电动势。 解： R E感作用在导体棒上，使导体
L
E静 dl 0
E E静 E感
B 在稳恒条件下，一切物理量不随时间变化， 0 t 静电场的环路定理 E dl 0
L
15
dB 增加 k ，求空间的感生电场的分布情况。 dt 解： 由于磁场均匀增加，圆形磁场区 R 域内、外 E感 线为一系列同心圆； 1. r < R 区域： 作半径为 r 的环形路径; o r 设涡旋电场的绕向也为逆时针方向。 B dB B E感 dl S t dS S dt dS
11-2动生电动势
v v
方法二
作辅助线，形成闭合回路 作辅助线，形成闭合回路CDEF
r r Φ = ∫ B• dS =
S
∫
a+b
a
εi = −
µ0 Ix a + b ln = 2π a dΦ
dt
µ0 I xdr 2πr
I
方向
D→C →
v v
X
µ0 I a + b dx ln ) = −( 2π a dt µ0 Iv a + b ln =− 2π a
均匀磁场
转动
r 如图，长为L的铜棒在磁感应强度为 例 如图，长为 的铜棒在磁感应强度为 B
求：棒中感应电动势的大小 和方向。 和方向。
的均匀磁场中， 轴转动。 的均匀磁场中，以角速度 ω 绕O轴转动。 轴转动
ω ××××
×××× ××××
O
r A B××× ×
解：方法一
v v v 取微元 dε = ( v × B )⋅ dl
a
+++ + +
r v v f = −e(v × B)
非静电力 它驱使电子沿导线由a向 移动 移动。 它驱使电子沿导线由 向b移动。
v B v v
r f
b
端出现过剩负电荷， 由于洛仑兹力的作用使 b 端出现过剩负电荷， a 端出现过剩正电荷 。
v 在导线内部产生静电场 E
方向a→ 方向 →b 电子受的静电力
S
v S 的法线方向应选得与曲线 L
的积分方向成右手螺旋关系
S
L
v ∂B 是曲面上的任一面元上磁感应强度的变化率 ∂t
不是积分回路线元上的磁感应强度的变化率
大学物理之动生电动势和感生电动势
13
12.2 动生电动势和感生电动势
第12章 电磁感应
感应电动势做功，洛伦兹力不做功？
rr F ⋅V
r =(f +
r f
'
)
⋅
(vr
+
vr'
)
=
r f
⋅vr'+
fr'⋅vr
= −evBv '+ev ' Bv
Fr
r f'
−e
vrr' f
r B vr
Vr
=0
洛伦兹力做功为零。
14
12.2 动生电动势和感生电动势
=
1 2
Bθ L2
回路中的电动势
ω
εi
=
−
dΦm dt
= − 1 BL2 dθ 2 dt
= − 1 BωL2 2
方向由楞次定律确定：
A
θ
o
C
r B
方向沿 A→O AC 、CO段没有动生电动势 25
12.2 动生电动势和感生电动势
第12章 电磁感应
例：法拉第电机。设铜盘的半径为 R，角速度为ω。 求：盘上沿半径方向产生的电动势。
423） ） ）求 确 确导 定 定线vrvr元和× 上BBvr的与的电夹d动lr角的势θ夹d1,ε角=θ(2vr,
×
r B
)
⋅
r dl
dl υ -a
∫ 5）由动生电动势定义求解。ε =
+
vBdl
若 6）ε动> 生0，电则动ε势的的方方向向与：dlrr 若ε < 0，则 ε 的方向与 dl
−
同向； 反向。
动生电动势，等于从起点到终点的直导线所产 生的动生电动势 。
12.2 动生电动势和感生电动势
第12章 电磁感应
感应电动势做功，洛伦兹力不做功？
rr F ⋅V
r =(f +
r f
'
)
⋅
(vr
+
vr'
)
=
r f
⋅vr'+
fr'⋅vr
= −evBv '+ev ' Bv
Fr
r f'
−e
vrr' f
r B vr
Vr
=0
洛伦兹力做功为零。
14
12.2 动生电动势和感生电动势
=
1 2
Bθ L2
回路中的电动势
ω
εi
=
−
dΦm dt
= − 1 BL2 dθ 2 dt
= − 1 BωL2 2
方向由楞次定律确定：
A
θ
o
C
r B
方向沿 A→O AC 、CO段没有动生电动势 25
12.2 动生电动势和感生电动势
第12章 电磁感应
例：法拉第电机。设铜盘的半径为 R，角速度为ω。 求：盘上沿半径方向产生的电动势。
423） ） ）求 确 确导 定 定线vrvr元和× 上BBvr的与的电夹d动lr角的势θ夹d1,ε角=θ(2vr,
×
r B
)
⋅
r dl
dl υ -a
∫ 5）由动生电动势定义求解。ε =
+
vBdl
若 6）ε动> 生0，电则动ε势的的方方向向与：dlrr 若ε < 0，则 ε 的方向与 dl
−
同向； 反向。
动生电动势，等于从起点到终点的直导线所产 生的动生电动势 。
第19讲动生电动势与感生电动势
解：由 B 0, 与B同向 感生电场沿逆时针。 t
取逆时针回路, r < R 时
l Ei dl
B dS S t
l
Ei
dl
cos
0
B t
dS
cos
Ei
2
r
dB dt
r2
r dB Ei 2 dt
××××× ×××××××
r × × × × × × ×
×××××××
×R× × × × B
r > R时，
3. 动生电动势的计算
作为电源的这段运动导体杆，其中的洛仑兹力 是非静电力。
非静电力 对应的非静电场强 由电动势定义
Fk e(v B)
Ek
Fk e
v
B
i Ek dl
运动导线ab产生的动生电动势为
i
(v B) dl
l
例题1 有一半圆形金属导线在匀强磁场中作切 割磁力线运动。已知 v, B, R. 求动生电动势.
解：
d (v B)dl
dl Rd v B
vB sin900 dl cos
2
vBR cos d 2 vB2R 有效段！
b dl
d
v
0：与假定的方向相同
R
B
方向：a b
a
例题2 如图，长为L 的铜棒在匀强磁场中以角速度 ω绕 o 轴转动。求：棒中感应电动势的大小 和方向。
解：取如图所示微元(此微元暗示了假定的正方向)
C × × ×O× ×
B t
Ei Dx
L
d Ei dx cos
r dB dx cos
2 dt
r dB Ei 2 dt
逆时针
r cos h
电磁感应——动生电动势总结
b a
b
εi
3、应用计算式计算在磁场中运动导线上的动生电动势
K K 速度也可以不同， v、 B
在一般情况下，磁场可以不均匀,导体在磁场中运动时各部分的
K 和 l 也可以不相互垂直，在这些情况下计算
运动导体内产生的总动生电动势应采取这样的步骤：
K K 先以一端为起点，在位置 l 处选取线元 dl ，计算线元上产生的动
生电动势；进而对整个处于磁场中的运动导体部分作积分，得到
总动生电动势。
K K K dε 动 = (v × B ) ⋅ d l
ε动 = ∫
L
L
K K K (v × B ) ⋅ d l
对于闭合回路
ε 动 为正时，表示电动势 为负。因此，由上式算出的电动势有正负之分， K K ε 动 为负时，则表示电动势的方向逆着dl 的方向。 方向顺着 dl 的方向；
a
K v
K B
b
K f
K K u fb 1
K K u +v
K K K K P = ( f1 + f2 ) ⋅ (v + u ) K K K K K = (−ev × B − eu × B) ⋅ (v + u ) = −evBu + euBv = 0
总洛仑兹力与总速 度垂直，不做功！
讨 论
（2）回路中的电能从何而来？
ε动的正负来判断电动势的方向。
实验演示
3、动生电动势产生过程中的能量转换
每个电子受的洛仑兹力
K B⊗
K f2
a
−eK uFra bibliotekK K K f l = f1 + f 2 K K K f1 = − ev × B
K f1 K f2
大学物理 马文蔚 课堂笔记15
已知 R, h, , B, dB/dt, 求 I 解 如图取一半径为r ,宽度为dr的圆环, 则
dB dB i E k dl dS dS L S dt S dt dB 因 和 S 平行 dt
圆环中的感生电动势的大小为
R
h
B
L
+ +
1 BL2 2
上海师范大学
i 方向
(点 P 的电势高于点 O 的电势) 4 /15
例2 一导线矩形框的平面与磁感强度为 B 的均匀磁场相垂直.在此矩形框
上,有一质量为 m 长为
§8.2
动生电动势和感生电动势
其值较之导线的电阻值要大得很多. 若开始时, 细导体棒以初速度 v0 沿如图
场方向垂直的平面上绕棒的一端转动；
解 如图所示，铜棒绕O点转动,
线元上产生的动生电动势为
+ + +
+ + + +B+ + + + +
d i ( v B) dl vBdl
L
整段铜棒上的电动势为
o v + + +
+ + O P
i
0
vBdl 0 lBdl
上海师范大学
14 /15
§8 -3
自感和互感
例1 如图是一长直密绕螺线管,长度为l, 横截面积为S, 线圈的总匝数为N,
管中均匀磁介质的磁导率为, 试求其自感L. (忽略边缘效应)
解 一般方法: 先设通有电流 I
螺线管密度(单位长度的线圈数) n=N/l,
求得 B
大学物理Ⅱ2.1 动生电动势
磁力线运动。已知： v, B, R.
求：动生电动势。
dl Rd
vB
解：方法一
d
(
v
B
)
dl
vBdl cos
2
vBR cosd 2 vB2R 方向：a b
b
dl
d
v
R
B
a
动生电动势
第十一章 电磁感应 电磁场
解：方法二
b
作辅助线，形成闭合回路
i 0
v
半圆
ab
2RBv
动生电动势
第十一章 电磁感应 电磁场
1、在磁场中运动的导线内的感应电动势
由于导体运动而产生的感应电动势，称为动生
电动势。
dΦ B d S Bl d x
i
dΦ dt
Bl d x
dt
D
A
v
B l
C B dx
Blv
动生电动势
第十一章 电磁感应 电磁场
解
i
b (v B) dl
a
b
vBdl
a
B
vB(ab) 2vB R2 r2
O
v
R
r dl
b
a
动生电动势
第十一章 电磁感应 电磁场
2．在磁场中转动的线圈内的感应电动势
设矩形线圈ABCD
o
的匝数为N ,面积为S， 使这线圈在匀强磁场中
绕磁直的间固感。夹B，定应当角的 强 为与时轴 度 零t 之，t线 ，与间0经OenO与的过B轴转夹时之eB垂动角n O间O，
Bv sin dl
0L Bv sin dl
BvLsin
dl
v
L
B
动生电动势 典型结论
动生电动势与感生电动势
【解】由于金属棒处在通电导线的非均匀磁场中，因此必
须将金属棒分成很多长度元dx，规定其方向由A指向B。这样 在每一dx处的磁场可以看作是均匀的，其磁感应强度的大小为
B 0I
2x
根据动生电动势的公式可知，dx小段上的动生电动势为
d动
(v
B)
dl
Bv
cos
dx
0I
2x
vdx
由于所有长度元上产生的动生电动势的方向都相同，所以金
d
dt
d dt
S
B
dS
又根据电动势的定义可得
L EK dl
式中，EK为感生电场的电场强度。感生电场的电场强度是 非静电性场强。
则有
L EK
dl
d dt
B dS B dS
s
s t
dB
s
S t
若闭合回路是静止的，即所包围面积S不随时间变化，即
S 0 ，则上式可写成
t
B L EK dl s t dS
性场强为
Ek
fL (e)
vB
根据电动势的定义可得，动生电动势为
a
动
L Ek
dl
(v B) dl
b
上式是动生电动势的一般表达式。由上式可知，动生电动势
的方向是非静电性场强 Ek v B 在运动导线上投影的指向。
【例9-2】如下图所示，长直导线 中通有电流I＝10A，有一长l＝0.1m的 金属棒AB，以v＝4m·s-2的速度平行于 长直导线作匀速运动，棒离导线较近的 一端到导线的距离a＝0.1m，求金属棒 中的动生电动势。
1861年，英国物理学家麦克斯韦提出感生电场的假设，认为 由于磁场变化而产生一种电场，是这个电场使导体中自由电子作 定向运动而形成电流。麦克斯韦还认为，即使没有导体，这种电 场同样存在。这种由变化磁场激发的电场称为感生电场。
《大学物理》6.2动生电动势感生电动势解读
k
b
B B 1 2 dS 解: bc R S t t 2
B 0 t
× ×
O × × × ×
uc ub
a
× ×
上页
b E c
下页
四、涡电流
产生原因： 大块的金属导体处在变化的磁场中时，通过金属 块的磁通量发生变化，从而产生感应电动势，在 金属内部形成电流，称为涡电流。 涡电流特点：
A
G
E
B
。。
下页
如何度量这种本领？ ε----电动势
上页
电动势： 电源把单位正电荷经内电路从 负极移到正极的过程中，非静 电力Fk所作的功 从场的观点： 非静电力对应非静电场
A非 q
q
E0
Fk qEk A非 Fk dl q Ek dl Ek dl
d 1.热效应： i dt
I
i
R
I(ω)
Q I 2 Rt 2
表明： 交流电频率越高发热越多——感应加 热原理
I(ω)
I(ω) I(ω)
I’
2.磁效应： 阻尼摆
上页 下页
小结：
动生电动势：磁场分布不变, 回路或导线在磁场中运动而引起的感应电动
势 感生电动势：导体回路不动,磁场随时间发生变化而引起的感应电动势
静电场
静止电荷
涡旋电场
变化磁场
有源场
无源场
上页 下页
感生电动势的计算 法拉第电磁感应定律
i
L
d d Ek dl
dt
dt
S B d S
因为回路固定不动，磁通量的变化仅来自磁场的变化
b
B B 1 2 dS 解: bc R S t t 2
B 0 t
× ×
O × × × ×
uc ub
a
× ×
上页
b E c
下页
四、涡电流
产生原因： 大块的金属导体处在变化的磁场中时，通过金属 块的磁通量发生变化，从而产生感应电动势，在 金属内部形成电流，称为涡电流。 涡电流特点：
A
G
E
B
。。
下页
如何度量这种本领？ ε----电动势
上页
电动势： 电源把单位正电荷经内电路从 负极移到正极的过程中，非静 电力Fk所作的功 从场的观点： 非静电力对应非静电场
A非 q
q
E0
Fk qEk A非 Fk dl q Ek dl Ek dl
d 1.热效应： i dt
I
i
R
I(ω)
Q I 2 Rt 2
表明： 交流电频率越高发热越多——感应加 热原理
I(ω)
I(ω) I(ω)
I’
2.磁效应： 阻尼摆
上页 下页
小结：
动生电动势：磁场分布不变, 回路或导线在磁场中运动而引起的感应电动
势 感生电动势：导体回路不动,磁场随时间发生变化而引起的感应电动势
静电场
静止电荷
涡旋电场
变化磁场
有源场
无源场
上页 下页
感生电动势的计算 法拉第电磁感应定律
i
L
d d Ek dl
dt
dt
S B d S
因为回路固定不动，磁通量的变化仅来自磁场的变化
动生电动势
b
+ +
F + m+
+
v +
+ + +
+ -+ a+
+ + + +
产生动生电动势的非静电力就是洛仑兹力。 单位正电荷的洛仑兹力
Fm Ek v B e
太原理工大学大学物理
运动导体上的动生电动势 i l ( v B) dl 若为闭合导体 i ( v B) dl
+Q + +
+ + + + + + +
+ + +
+
+
+ +
P
1 2 BL 2
B + +
+
o
+ + +
+
+
+
+ + + + + +
在op段中应为由o指向p
+ + +
太原理工大学大学物理
非均匀磁场
导体平动
I 例4 无限长载流直导体通有 电流I，方向向上。导线ab垂 直于直导线且两者在同一平 面内，a、b距直导线的距离 分别为l1和l2，导线ab以速度v 在平面内向上运动，求ab两 端的电势差。
m Bvtdx l
l2
1
0 I l2 vt ln 2 l1
0 I vtdx 2x
B
d m 0 I l2 i v ln dt 2 l1
大学物理动生电动势和感生电动势全篇
第十三章电磁感应
步骤：
dm
dt
b
a (v B) dl
1） 约定 右旋
2）求磁通
3）根据公式计算
1）取线元 dl ，并规定其方向
2）
写出
d
(v
B)
dl
3）确定积分范围，并积分
若结果 0,则
说明 实 与 相反
若结果 0,则
说明 实与 dl 相反
10 - 2 动生电动势和感生电动势
第十三章电磁感应
感生电场和静电场的对比
E静 和 Ek 均对电荷有力的作用.
静电场是保守场 L E静 dl 0
感生电场是非保守场
dΦ L Ek dl dt 0
静电场由电荷产生；感生电场是由变化的磁 场产生 .
10 - 2 动生电动势和感生电动势
第十三章电磁感应
例：将磁铁插入非金属环中，环内有无感
坩锅外的线圈中通交流电 电磁炉：交变磁场作用于金属锅底，产生
大量涡流
2. 电磁阻尼摆
涡电流的弊
热效应过强、温度过高， 易破坏绝缘，损耗电能，还可能造成事故
10 - 2 动生电动势和感生电动势
第十三章电磁感应
减少涡流 1、选择高阻值材料（硅钢、矽钢等） 2、多片铁芯组合
感生电场充当着产生感应电动势
的非静电力。
闭合回路中的感生电动势
L
Ek
dl
dΦ dt
10 - 2 动生电动势和感生电动势
第十三章电磁感应
闭合回路中的感生电动势
L
Ek
dl
dΦ dt
Φ SB dS
d
L Ek
dl
dt
B dS
S
S不变
大学物理课件-动生电动势和感生电动势
加速器的种类很多，用途也各不同，有静电加速 器、电子回旋加速器、电子感应加速器、同步辐射加 速器……等等。电子感应加速器主要用于核物理的研 究，用被加速的电子轰击各种靶时，将发出穿透力很 强的电磁辐射。另外电子感应加速器还应用于工业探 伤或医疗癌症。目前，我国最大的三个加速器是北京 的高能粒子加速器、合肥的同步辐射加速器、兰州的 重离子加速器。
12.3
动生电动势与感生电动势
根据法拉第电磁感应定律，只要穿过回路的磁通 量发生了变化，在回路中就会有感应电动势产生。 引起磁通量变化的原因不外乎两条： 其一是 磁场不变，回路相对于磁场有运动；
其二是 回路在磁场中虽无相对运动，但是磁场
在空间的分布随时间变化。 将前一原因产生的感应电动势称为动生电动势， 而后一原因产生的感应电动势称为感生电动势。
××××××××××××
E涡
v
f
B
v
f
B
由于电子感应 加速器的电磁铁用 交流电激励，所以 导致磁场从而涡旋 电场的方向是交变 的，而且电子受到 的洛仑兹力也并非 总是指向圆心。因 此，图示情况下只 有在第一个四分之 一周期内，电子才 受到感生电场的加 速，并且洛仑兹力 的方向指向圆心。
实际上，若交流电的周期为 50 Hz ，则在磁场变 化的第一个四分之一周期（约5ms 的时间）内，电子 就能在感生电场的作用下，在圆形轨道上经历回旋数 十圈的持续加速，从而获得足够高的能量，并在第一 个四分之一周期结束时被引出加速器至靶室。
l
2. 动生电动势的计算 计 算 动 生 电 动 势 分 类 均匀磁场
平动 转动 非均匀磁场
方 法
d m i dt
i (v B) dl
l
产生动生电动势的条件 ①有磁场 ②有导体 ③导体相对观察者（磁场）运动
大学物理(8.2.2)--动生电动势感生电动势
，求金
属
杆中
的
动生
电
动B 势
。O′
距 a 点为 l 处取一线元矢d量l v r l sin
b
该，处 的 非 静 电 场 场 强 为 ：
Ek
v
B
r
Ek
Ek vB lB sin
该线元运动时产生的电动势 di Ek dl
al
：di Ek dl cos(900 ) Ek dl sin lBdl sin 2
计算该线元运动时产生的电动势 di
， Ek dl
(v
B)
dl
（ 3 ）：计算该导线运动时产生的动生电动
势
εi
l
(v
B)
dl
i 0 电动势方向与积分路线方向相同 i 0 电动势方向与积分路线方向相反
例 8-3: 一长度为 L 的金属杆 ab 在均匀B磁场 中绕平行于磁
的
金属棒，金属棒绕其一端 O 顺时针匀速转动，转动角速度为
，
O 点至导线的垂直距离为 a ，
解
：金距1属)O选棒点O求所为：在l方M处处1向)的取当为金磁一金积属感线属分棒应元棒路内强矢转线d感度l量至应为与电B：v长动直2势l0导的aI 线,大方平小向行和，方如向图I；中
该，处 的 非 静 电 场 场 强 为 ：
场方向
磁场
′ 的定轴 OO′ 转动，已知杆的角速度为 ，杆相对于 的方位角为 θ ，求金属杆中的动生电动势B 。O′
b
L
a
O
例 8-3:
大学物理8-2 动生电动势和感生电动势
洛伦兹力
Fm
(e)v
B
平衡时
Ek
Fm
Fm e
Fe
v
eEk
B
+ B
+Leabharlann + +Fe++P++++
+ +
++
+ +
v + + + - + + + +
+
+Fm+
-
+ -
+
+
+
+ + + O+ + + +
i
OP Ek dl
(v
B)
dl
OP
l
设杆长为 l
i
vBdl vBl
0
+ +
+ +
+++++++
i
1 2
BL2
方i 向 O P
（点P 的电势高于点O 的电势）
例2 一导线矩形框的平面与磁感强度为 的B 均匀磁 场相垂直.在此矩形框上,有一质量为 长m为 的可l 移 动的细导体棒 ;矩形M框N还接有一个电阻 ,其值较之R
导线的电阻 值要大得很多.若开始时,细导体棒以速度 沿如图所示v0的矩形框运动,试求棒的速率随时间变化
产生感生电动势的非静电场
感生电场
麦克斯韦尔假设 变化的磁场在其周围空间激发一 种电场,这个电场叫感生电场 . Ek
涡旋电场的环流
动生电动势的公式
动生电动势的公式
动生电动势是指在一个固定的量子系统中，当外加电场和其它外
力施加了一个小变化时，核系统内部关联的变化。
它是一种可以用来
描述量子物理系统中特定状态转换时能量消耗的概念。
电场对本征态
的影响，通常用动生电动势公式来表示：V(r)=-∫E(r)*d(r), 其中
V(r)是动生电动势，E(r)是应用到波函数上的电场，D(r)是以r为自
变量的波函数积分。
另外，动生电动势也可以用来描述单子及其领域内电子的变化：
V(R)=−∫E(R)·d(R)，其中V(R)是动生电动势，E(R)是在波函数上施
加的电场，D(R)是以R为自变量的波函数积分。
在这种情况下，动生
电动势可以用来表达电子状态转换时电子原子结构及结合能等的变化。
动生电动势可以用来计算和分析物质的性质，如离子极化能、化
学键能、分子极化能等。
另外，也可以用来计算电子结构及光吸收、
电磁，热学等方面的性质。
最后，动生电动势也可以用来研究光学特性，如线谱强度、电离概率等，为材料科学的发展提供重要支持。
动生电动势
求导线ab中的动生电动势，并判断哪端电势较高。
解：（1）应用i
ba
(v
B)
d
l
求解
I
a d
在导线ab上取一线元dr,距长直载流 r
导线r,方向向右。
v
L dr
b
di
(v B)d r
vBd r
0Iv 2r
dr
ab
ba
d
dL d
d r 0Iv
2r
ln 0 Iv d L
2
d
由于ab 0,表明电动势的方向由a 指向b,b 端电势较高。 7
（2）应用电磁感应定律求解
设某时刻导线ab 到U
形框底边的距离为x，取顺
时针方向为回路的正方向,
则该时刻通过回路abooa
的磁通量为
a
v
X b
I
O
O
r
dr
Φ s BdS
d d
L
0I 2r
x
d
r
0Ix 2
ln
d
d
L
ab
d dt
I 0
2
ln(
d
d
L
)
d d
x t
0 Iv 2
ln
dL d
即沿顺a时b 针0方表向示。电因动此势在的导方线向a与b上所,选电回动路势由方a指向向相b同,,
v
en
A
D o
化的，这种电动势称为交变电动势。在交变电动势的
作用下，线圈中的电流也是交变的，称为交变电流或
交流。
15
i I
0
o
I0
t
交变电动势和交变电流
16
解一 ：取线元 dl
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
=B .lω sin900 dl cos1800
v
B v ×B
ω
O
dl lL
[例4] 一金属杆在匀强磁场中转动，已知2-3：-4
B，ω ，L 。求：动生电动势。
解一：
ε . d = ( v ×B ) dl
v = lω
=B .lω sin900 dl cos1800
v
B v ×B
ω
O
dl lL
[例4] 一金属杆在匀强磁场中转动，已知2-3：-4
= Bv sina dl
v ×B
dl
a
L
v
B
[例2] 已知：v ，B，a ，L 。
2-3-4
求：ε
ε . d = ( v ×B ) dl
= v B sin900 dl cos (900 a )
= Bv sina dl
ε = Bv sina dl
v ×B
dl
a
L
v
B
[例2] 已知：v ，B，a ，L 。
v ×B
dl
a
L
v
B
[例2] 已知：v ，B，a ，L 。
2-3-4
求：ε
ε . d = ( v ×B ) dl
= v B sin900 dl cos (900 a )
v ×B
dl
a
L
v
B
[例2] 已知：v ，B，a ，L 。
2-3-4
求：ε
ε . d = ( v ×B ) dl
= v B sin900 dl cos (900 a )
B，ω ，L 。求：动生电动势。
解一：
ε . d = ( v ×B ) dl
v = lω
=B .lω sin900 dl cos1800
v
ε=
Bω
L 0
l
dl
B v ×B
ω
O
dl lL
[例4] 一金属杆在匀强磁场中转动，已知2-3：-4
B，ω ，L 。求：动生电动势。
解一：
ε . d = ( v ×B ) dl
2-3-4
v ×B v
B
[例1] 直金属杆在均匀 磁场中做切割磁力线运动。
求：动生电动势。
1. 选择 dl 方向；
dl
2. 确定 v × B 的方向；
3. 确定 dl 所在处的
B 及v ；
2-3-4
v ×B v
B
[例1] 直金属杆在均匀 磁场中做切割磁力线运动。 求：动生电动势。
2-3-4
v ×B
εd i = ( v ×B ) . dl ε i =l ( v×B ) . dl
v
fm
方向指向d l 为正
[例1] 直金属杆在均匀
2-3-4
磁场中做切割磁力线运动。
v
B
[例1] 直金属杆在均匀
2-3-4
磁场中做切割磁力线运动。
求：动生电动势。
v
B
[例1] 直金属杆在均匀
2-3-4
磁场中做切割磁力线运动。
v ×B
dl
dθ θ
θv
R B
[例3] 有一半圆形金属导线在匀强磁场2中-3-4
作切割磁力线运动。已知：v ，B ，R 。
求：动生电动势。
. d = ( v ×B ) dl
ε . = v ×B dl cos (v ×B ，dl )
= vB sin900 dl cosθ
v ×B
dl
dθ θ
θv
R B
Ek=
fm e
++ + ++
2-3-4
v ×B
v
fm
非静电性电场的场强为：
Ek=
fm e
= v×B
++ + ++
2-3-4
v ×B
v
fm
非静电性电场的场强为：
Ek=
fm e
= v×B
所以动生电动势为：
++ + ++
2-3-4
v ×B
v
fm
非静电ቤተ መጻሕፍቲ ባይዱ电场的场强为：
Ek=
fm e
= v×B
所以动生电动势为：
ε ε 5. 确定 d i 及 i ε . d i = ( v ×B ) dl
[例1] 直金属杆在均匀 磁场中做切割磁力线运动。 求：动生电动势。
2-3-4
v ×B
1. 选择 dl 方向；
dl
2. 确定 v × B 的方向；
v
3. 确定 dl 所在处的
B
B 及v ；
4. 确定 dl 与 v × B 的夹角；
作切割磁力线运动。已知：v ，B ，R 。
求：动生电动势。
ε . d = ( v ×B ) dl
v ×B
dl
dθ θ θv
R B
[例3] 有一半圆形金属导线在匀强磁场2中-3-4
作切割磁力线运动。已知：v ，B ，R 。
求：动生电动势。
. d = ( v ×B ) dl
ε . = v ×B dl cos (v ×B ，dl )
R B
[例3] 有一半圆形金属导线在匀强磁场2中-3-4
作切割磁力线运动。已知：v ，B ，R 。
求：动生电动势。
. d = ( v ×B ) dl
ε . = v ×B dl cos (v ×B ，dl )
= vB sin900 dl cosθ
ε =vB
π2 π2
cosθ
R dθ
=vB 2R
v ×B
ε ε 5. 确定 d i 及 i ε . d i = ( v ×B ) dl = v B dl cos00
[例1] 直金属杆在均匀 磁场中做切割磁力线运动。 求：动生电动势。
2-3-4
v ×B
1. 选择 dl 方向；
dl
2. 确定 v × B 的方向；
v
3. 确定 dl 所在处的
B
B 及v ；
4. 确定 dl 与 v × B 的夹角；
2-3-4
第四节
动生电动势
2-3-4 动生电动势
2-3-4
2-3-4 动生电动势
2-3-4
动生电动势：由于导线和磁场作相对运动所 产生的电动势。
2-3-4 动生电动势
2-3-4
动生电动势：由于导线和磁场作相对运动所 产生的电动势。
感生电动势：由于磁场随时间变化所产生的 电动势。
2-3-4 动生电动势
ε ε 5. 确定 d i 及 i ε . d i = ( v ×B ) dl = v B dl cos00 ε i =v B dl
[例1] 直金属杆在均匀 磁场中做切割磁力线运动。 求：动生电动势。
2-3-4
v ×B
1. 选择 dl 方向；
dl
2. 确定 v × B 的方向；
v
3. 确定 dl 所在处的
v = lω
=B .lω sin900 dl cos1800
v
ε=
Bω
L 0
l
dl
=
1 2
Bω
L
2
B v ×B
ω
O
dl lL
[例4] 一金属杆在匀强磁场中转动，已知2-3：-4
B，ω ，L 。求：动生电动势。
解一：
ε . d = ( v ×B ) dl
v = lω
=B .lω sin900 dl cos1800
dl
dθ θ θv
R B
[例4] 一金属杆在匀强磁场中转动，已知2-3：-4
B，ω ，L 。求：动生电动势。
解一：
v ω
B O L
[例4] 一金属杆在匀强磁场中转动，已知2-3：-4
B，ω ，L 。求：动生电动势。
解一：
v
ω
B
O
dl lL
[例4] 一金属杆在匀强磁场中转动，已知2-3：-4
B，ω ，L 。求：动生电动势。
2-3-4
求：ε
a
L
v
B
[例2] 已知：v ，B，a ，L 。
2-3-4
求：ε
ε . d = ( v ×B ) dl
a
L
v
B
[例2] 已知：v ，B，a ，L 。
2-3-4
求：ε
ε . d = ( v ×B ) dl
dl
a
L
v
B
[例2] 已知：v ，B，a ，L 。
2-3-4
求：ε
ε . d = ( v ×B ) dl
ε . i = l E k dl
++ + ++
2-3-4
v ×B
v
fm
非静电性电场的场强为：
Ek=
fm e
= v×B
所以动生电动势为：
ε . i = l E k dl
. =
l
(
v×B
)
dl
++ + ++
2-3-4
v ×B
v
fm
非静电性电场的场强为：
Ek=
fm e
= v×B
所以动生电动势为：
ε . i = l E k dl
. =
l
(
v×B
)
dl
εd i = ( v ×B ) . dl
++ + ++
2-3-4
v ×B