大学物理动生电动势和感生电动势共36页文档
动生电动势和感生电动势
§ 6-2 动生电动势和感生电动势动生电动势：回路或其一部分在磁场中的相对运动所产生的感应电动势。
感生电动势：仅由磁场的变化而产生的感应电动势。
动生电动势B图6-5动生电动势动生电动势的产生可以用洛伦兹力来解释。
长为I的导体棒与导轨构成矩形回路abed平放在纸面内，均匀磁场B垂直纸面向里。
当导体棒ab以速度v沿导轨向右滑动时，导体棒内自由电子也以速度v随之一起向右运动。
每个自由电子受到的洛伦兹力为F = (- e) v B ,方向从b指向a，在其作用下自由电子向下运动。
如果导轨是导体，在回路中将形成沿着abed逆时针方向的电流。
如果导轨是绝缘体，则洛伦兹力将使自由电子在a端累积，从而使a端带负电，b端带正电，在ab棒上产生自上而下的静电场。
当作用在自由电子上的静电力与洛伦兹力大小相等时达到平衡，ab间电压达到稳定值，b 端电势比a端高。
这一段运动导体相当于一个电源，它的非静电力就是洛伦兹力。
电动势定义为单位正电荷从负极通过电源内部移到正极的过程中，非静电力K所作的功，即F K v B .-e动生电动势为+ b名=J K d \ =f (v 汉B) d l . (6.4)- a ' '均匀磁场情况：若v — B，则有；=Bl v;若导体顺着磁场方向运动，v B,则有v B = 0，没有动生电动势产生。
因此，可以形象地说，只有当导线切割磁感应线而运动时，才产生动生电动势。
普遍情况：在任意的恒定磁场中，一个任意形状的导线线圈L(闭合的或不闭合的)在运动或发生形变时，各个线元dl 的速度v 的大小和方向都可能是不同的。
这时，在整 个线圈L 中产生的动生电动势为=(v B ) d l .(L)图6-6洛伦兹力不作功洛伦兹力对电荷不作功：洛伦兹力总是垂直于电荷的运动速度，即 F v_ v ，因此洛 伦兹力对电荷不作功。
然而，当导体棒与导轨构成回路时会有感应电流出现，这时感应 电动势却是要作功的。
12_2_3动生电动势和感生电动势_11_10
Fm
+ v
+
+ + + +
3
12 – 2、3 动生电动势和感生电动势
第十二章电磁感应
由于洛仑兹力的作用使b 端出现过
剩负电荷，a 端出现过剩正电荷 。 在导线内部产生静电场 E
方向ab
a
+++ + +
Fe
Fe
B
电子受的静电力 Fe eE
平衡时 Fe Fm
2 2
2 2
方向沿 ox轴反向
N
dv B l v F ma m R l dt R F 2 2 v dv t B l 则 v0 v 0 mR dt o
B
v
M
x
计算得棒的速率随时间变化的函数关系为
v v0 e
( B 2l 2 mR ) t
19
例5 一无限长直导线载有电流 I，与其共面有一 三角形线圈ABC以速率 v 垂直离开长导线，求 处于图中位置时线圈中的感应电动势。
f m BI i l
fm f外
fm I i v B
P外＝f外 v BI i lv
P电＝ i I i BlvIi P外
电能由外力作功转化而来
9
12 – 2、3 动生电动势和感生电动势
I a
v
dx
L x
m
aL
a
0 Iy Iy a L 0 dx ln 2x 2 a
B
16
回路中的感应电动势为：
0 I dy a L d m ln i dt 2 dt a dy I v dt
动生电动势和感生电动势
§6-2 动生电动势和感生电动势动生电动势：回路或其一部分在磁场中的相对运动所产生的感应电动势。
感生电动势：仅由磁场的变化而产生的感应电动势。
一 动生电动势图6 - 5 动生电动势动生电动势的产生可以用洛伦兹力来解释。
长为l 的导体棒与导轨构成矩形回路abcd 平放在纸面内，均匀磁场B 垂直纸面向里。
当导体棒ab 以速度v 沿导轨向右滑动时，导体棒内自由电子也以速度v 随之一起向右运动。
每个自由电子受到的洛伦兹力为B v F ⨯-)(=e ,方向从b 指向a ，在其作用下自由电子向下运动。
如果导轨是导体，在回路中将形成沿着abcd 逆时针方向的电流。
如果导轨是绝缘体，则洛伦兹力将使自由电子在a 端累积，从而使a 端带负电，b 端带正电，在ab 棒上产生自上而下的静电场。
当作用在自由电子上的静电力与洛伦兹力大小相等时达到平衡，ab 间电压达到稳定值，b 端电势比a 端高。
这一段运动导体相当于一个电源，它的非静电力就是洛伦兹力。
电动势定义为单位正电荷从负极通过电源内部移到正极的过程中，非静电力K 所作的功，即B v F K ⨯=-=e.动生电动势为ε⎰⎰+-⋅⨯=⋅=l B v l K d )(d ba .(6.4)均匀磁场情况：若v ⊥ B , 则有ε = B l v ；若导体顺着磁场方向运动，v // B ，则有 v ⨯ B = 0，没有动生电动势产生。
因此，可以形象地说，只有当导线切割磁感应线而运动时，才产生动生电动势。
普遍情况：在任意的恒定磁场中，一个任意形状的导线线圈L (闭合的或不闭合的)在运动或发生形变时，各个线元d l 的速度v 的大小和方向都可能是不同的。
这时，在整个线圈L 中产生的动生电动势为ε l B v d )()(⋅⨯=⎰L .(6.5)图6 - 6 洛伦兹力不作功洛伦兹力对电荷不作功：洛伦兹力总是垂直于电荷的运动速度，即v ⊥F v ，因此洛伦兹力对电荷不作功。
12.2 动生电动势和感生电动势
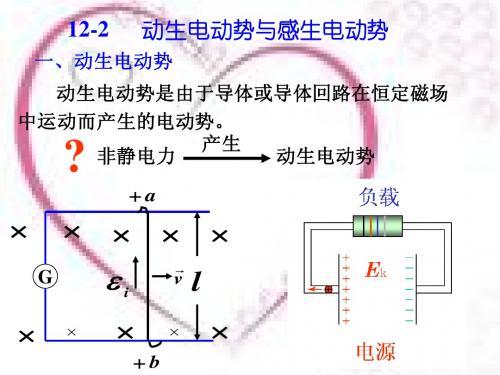
此时电荷积累停止， 两端形成稳定的电势差 两端形成稳定的电势差。 此时电荷积累停止，ab两端形成稳定的电势差。 洛仑兹力是产生动生电动势的根本原因 洛仑兹力是产生动生电动势的根本原因. 是产生动生电动势的根本原因
动生电动势的公式
非静电力
f = −e(v × B)
f 定义 Ek为非静电场强 Ek = = v ×B −e
S
A B ××× ×
ω ××v × ×
非均匀磁场
例 一直导线CD在一无限长直电流磁场中作 一直导线 在一无限长直电流磁场中作 切割磁力线运动。 切割磁力线运动。求：动生电动势。 动生电动势。 解：方法一
dε = ( v × B )⋅ dl I l dl µ0I 0 0 D sin90 dl cos180 =v C 2πl b a µ0vI dl =− 方向 D→C → 2πl µ0vI a+b dl µ0vI a + b ε =− ∫a l = − 2π ln a 2π
×××× ⊗ o ×××× B ×××× h
C
∂B ∂t
××
L
D
解:
ε i = ∫ E涡 • dl
L
r dB E涡 = 2 dt
dε = E涡 • dl r dB dl cosθ = 2 dt
h dB dl = 2 dt
⊗o
B
⊗
θ
∂B ∂t
E涡
r h
l dl
L
θ
C
D
h dB 1 dB εCD = ∫L dl = 2hL dt 2 dt
O
解：方法一 取微元
dε = ( v × B )⋅ dl
= Bvdl = Blωdl
εi = ∫ dεi = ∫0 Blωdl
大学物理动生电动势与感生电动势
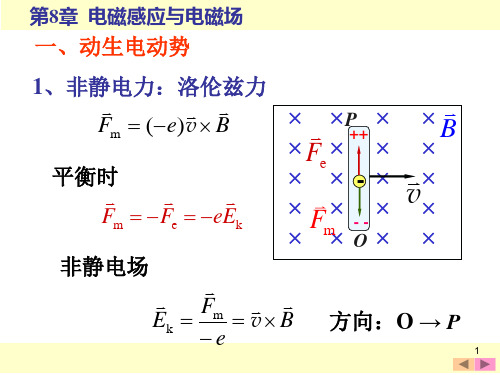
一、动生电动势
1、非静电力：洛伦兹力
Fm (e)v B
平衡时 Fm Fe eEk
×
×P
++
×
×
B
× Fe × × ×
× × - × ×
v ×
×
Fm××
--
O
× ×
× ×
非静电场
Ek
Fm e
v
B
方向：O → P
1
第8章 电磁感应与电磁场
2、动生电动势的计算
B 0 t
为圆心的圆。
Br
解 i Ei dl
R
•
o
L
Eidl Ei dl
L
L
dl Ei
15
第8章 电磁感应与电磁场
Ei 2πr
dΦm dt
外部 ( r >R ) Φm BπR2
Ei
R2 2r
B t
内部 ( r <R ) Φm Bπr 2
Ei
1 2
B t
r
B
R
•
o
r
B
O
r
16
先求线圈所在处的磁通量,再求磁通 量的变化率。
感生电动势计算方法 2
运用Ｅi的环流定理, 即
i
l Ei dl
dΦ dt
14
第8章 电磁感应与电磁场
例1一个半径 为R 的长直载流螺线管，内部磁
场强度为 B , 现已知 B / t 为大于零的恒量。
求管内外的感生电场。 分析电场线是一系列以O
由电动势的定义，有
说明：
i OP Ek dl
(v
B)
dl
动生电动势和感生电动势
Ek
1 2
B t
r
1 2
kr
2. r > R 区域
作半径为 r 的环形路径，并以逆
时针为回路绕向，则同理有
2rEk
S
B t
ds
R2k
R
o
r
r
B
1 B R2 1 R2
Ek 2 t
r
k 2r
Foundation - SJYGGF
§ 13.2 动生电动势和感生电动势
Nov 5, 2002 9/33
随时间均匀增加， dB k dt
若铝圆盘的电导率为γ，求盘内 的感应电流。
见书P212页，例4
R
解： 取半径为r、宽为dr的圆环微 元，并以逆时针方向为正方向，则 微元环中元电动势为
d L Ek dl L Ek dl
1 kr 2r dl kr2
20
o
r
dr
B
微元环中的电阻为 dR 1 2r hdr
Foundation - SJYGGF
§ 13.2 动生电动势和感生电动势
Nov 5, 2002 21/33
4) 电度表记录电量
电度表记录用电量，就是
利用通有交流电的铁心产生交
变的磁场，在缝隙处铝盘上产
o
生涡电流，涡电流的磁场与电
磁铁的磁场作用，表盘受到一
转动力矩，使表盘转动。
o’
Foundation - SJYGGF
感生电动势
1. 感生电动势——回路不动或不变，因磁场随时间变 化产生的电动势。相应的电流称为感生电流。
2. 感生电动势的起源——感生电场Ek 1) Maxwell感生电场（涡旋电场）假设
Maxwell 1861年首先从理论上预言感生电场的存在，后 被Hertz的电磁波实验所证实。Maxwell假设： 变化的磁场要在其周围空间激发一种电场——感生电场
《大学物理》6.2动生电动势感生电动势解读
b
B B 1 2 dS 解: bc R S t t 2
B 0 t
× ×
O × × × ×
uc ub
a
× ×
上页
b E c
下页
四、涡电流
产生原因： 大块的金属导体处在变化的磁场中时，通过金属 块的磁通量发生变化，从而产生感应电动势，在 金属内部形成电流，称为涡电流。 涡电流特点：
A
G
E
B
。。
下页
如何度量这种本领？ ε----电动势
上页
电动势： 电源把单位正电荷经内电路从 负极移到正极的过程中，非静 电力Fk所作的功 从场的观点： 非静电力对应非静电场
A非 q
q
E0
Fk qEk A非 Fk dl q Ek dl Ek dl
d 1.热效应： i dt
I
i
R
I(ω)
Q I 2 Rt 2
表明： 交流电频率越高发热越多——感应加 热原理
I(ω)
I(ω) I(ω)
I’
2.磁效应： 阻尼摆
上页 下页
小结：
动生电动势：磁场分布不变, 回路或导线在磁场中运动而引起的感应电动
势 感生电动势：导体回路不动,磁场随时间发生变化而引起的感应电动势
静电场
静止电荷
涡旋电场
变化磁场
有源场
无源场
上页 下页
感生电动势的计算 法拉第电磁感应定律
i
L
d d Ek dl
dt
dt
S B d S
因为回路固定不动，磁通量的变化仅来自磁场的变化
§10-2. 动生电动势与感生电动势
（3）感生电场是无源场。
S
E dS 0.....( 4)
B t E
• 涡旋电场无源其电里力线是闭合曲线。 3、感生电动势的非静电力—感生电场对电 11 荷的作用力 F eE 。
4.感生电场和静电场的比较 (1)相同点：都对电荷有作用力。
不同点 产生的原因 电力线 静电场 电荷 电力线有头有尾
I B1 0 2d
B2 2 (d a)
0 I
I
1 : B DA 2 : B CB 回路中总感应电动势方向沿顺
时针．
1
d
B 2
a
15
10-11）
在金属杆上取距左边直导线为，则
I B1 0 2r
B B1 B2
图中电动势的方向：从负极a正极b;
b
(1)动生电动势的大小：
（3）式 (v B) dl 仅适用 a
a
f
v
于计算切割磁场线的导体中的感 应电动势。 (4)积分是沿着运动的导线进行的。
3
（5）若ab导体为闭合回路则动生电动势为： (v B) dl .....(1)
0…………（2）
10
（2）感生电场是非保守场。
d B l E dl dt SB d S S t d S........(10.4)
B dS 代入（2）式，得： S
n S l
• dS的正方向与l成右手螺旋关系
b
r Iv Iv dr d l sin 0 Iv sin dl 0 dr0 a 2 r r 2 r d 2 r 0 Iv d l sin ln 2 d v B：b a
大学物理动生电动势和感生电动势全篇
第十三章电磁感应
步骤：
dm
dt
b
a (v B) dl
1） 约定 右旋
2）求磁通
3）根据公式计算
1）取线元 dl ，并规定其方向
2）
写出
d
(v
B)
dl
3）确定积分范围，并积分
若结果 0,则
说明 实 与 相反
若结果 0,则
说明 实与 dl 相反
10 - 2 动生电动势和感生电动势
第十三章电磁感应
感生电场和静电场的对比
E静 和 Ek 均对电荷有力的作用.
静电场是保守场 L E静 dl 0
感生电场是非保守场
dΦ L Ek dl dt 0
静电场由电荷产生；感生电场是由变化的磁 场产生 .
10 - 2 动生电动势和感生电动势
第十三章电磁感应
例：将磁铁插入非金属环中，环内有无感
坩锅外的线圈中通交流电 电磁炉：交变磁场作用于金属锅底，产生
大量涡流
2. 电磁阻尼摆
涡电流的弊
热效应过强、温度过高， 易破坏绝缘，损耗电能，还可能造成事故
10 - 2 动生电动势和感生电动势
第十三章电磁感应
减少涡流 1、选择高阻值材料（硅钢、矽钢等） 2、多片铁芯组合
感生电场充当着产生感应电动势
的非静电力。
闭合回路中的感生电动势
L
Ek
dl
dΦ dt
10 - 2 动生电动势和感生电动势
第十三章电磁感应
闭合回路中的感生电动势
L
Ek
dl
dΦ dt
Φ SB dS
d
L Ek
dl
dt
B dS
S
S不变
动生电动势与感生电动势
Science &Technology Vision 科技视界1动生电动势如图1,一根金属棒在匀强磁场中沿与棒和磁场垂直的方向以速度V0向右运动。
自由电荷(电子)随棒运动。
必然受到洛仑磁力作用,而发生运动。
电子沿棒运动的速度为U。
这样自由电子具有随金属棒运动的速度V0同时还有沿棒运动的速度U,故自由电子相对磁场的合速度为V0。
金属棒ab 两端因正负电荷分别积累,而形成电动势,Uab>0。
图1由左手定则可知,由于自由电子相对磁场以速度V 运动,一定会受到洛仑磁力F 洛。
当F 洛的分力F1与F 外平衡,F 洛的另一分力F2与电场力FE 平衡时,金属棒两端建立了稳定的动生电动势。
F 洛=eBV 其分力F1=eBVcosα=eBu,F2=eBVsinα=eBV0金属棒ab 两端电动势U=BLV0,自由电子受到的电场力FE=eE=eBLV0/L=eBV0FE 与F2等大反向。
F 外与F1等大反向(图2)。
图2F E 与F 外的合力F'=eB V 02+U 2√=eBVH 合和F 洛等大反向。
此时自由电子受到的三个力F 洛、F 外、F E 作用达到平衡。
金属棒匀速垂直切割磁感线运动建立了稳定的电动势。
E=BLV 0从能量转化的观点来看:外力克服洛仑磁力的分力F1做功,机械能转化的电能。
在此过程中洛仑磁力起到中转能量的作用。
使机械能和电能之间发生转化。
那么洛仑磁力是否做功呢:F 洛的分力F 1与V 0反向做负功W1,另一分力F2与电子沿棒移动方向U 一致做正功W2,则有:W1=-F 1V 0t=-eBIV 0t W2=F 2Ut=eBV 0Ut W=W1+W1=0其实洛仑磁力F H 合与电子合速度V 垂直,其做功为零是肯定的。
我们可以看到动生电动势有以下几个特点:a.在能量转化上是机械能转化为电能。
b.洛仑磁力参与其全过程并传递能量,实现两种形式的能量转化。
c.因为洛仑磁力与自由电荷合速度方向垂直,洛仑磁力不做功。
第十三章第2次课 动生电动势和感生电动势
d dt
思考题： N
S
I
条形磁铁靠近线圈时， 线圈中那端电势高？
三角形线框靠近直导线时， 线框中电动势方向如何？
概念检测 如题图所示，一根长为l 的金属细杆ab绕竖直轴 O1O2以角速度在水平面内旋转，O1O2在离细杆a端l/3 处，若已知地球磁场在竖直方向的分量为B，则ab两 端间的电势差Uab O1 A. 大于零 B. 小于零 C. 因为没有电流， 所以Uab等于零
麦克斯韦提出了感生电场（涡旋电场）的概念
变化的磁场在其周围空间激发一 种电场，称为感生电场（涡旋电场）
——感生电场（涡旋电场）假设
麦克斯韦 (1831-1879)
变化的 激发 感生 作用 自由 引起 电荷 电场 磁场
感生电 动势
麦克斯韦假设(1861): 揭示了 电磁场的新效应。
感生电场：
Ei
R 2 dB Ei 2 r dt
r
(r R)
R dB 2 dt
Ei
变化的磁场只限于r≤R区域， 但它所激发的涡旋电场不限于 r≤R区域
o
R
r
(2) 如果将长度为l的导棒ab放在螺线管内，求导棒ab 两端的感生电动势
R
O
a
l
b
方法一： 在导棒上选一线元 dl
O
R
a
h
r
Ei
该线元上的感生电动势 d Ei dl
第十三章 电磁感应
一、电磁感应的基本现象
复习
二、楞次定律 闭合回路中感应电流的方向总是使得它所 激发的磁场来阻碍引起感应电流的磁通量的变 化。 三、法拉第电磁感应定律
四、动生电动势
dΦ dt
动生和感生电动势
目录
• 动生电动势 • 感生电动势 • 比较动生和感生电动势 • 实例分析 • 问题与讨论
01
CATALOGUE
动生电动势
定义与原理
定义
动生电动势是指由导体在磁场中运动而产生的感应电动势。
原理
根据法拉第电磁感应定律，当导体在磁场中运动时，导体中 的电子会受到洛伦兹力的作用，从而在导体两端产生电动势 。
感生电动势的大小取决于磁场的变化率。如果磁场变化很快，那么产生的电动势就很大。
应用比较
动生电动势在电力生产和传输中起着关键作用。例如，发电机是通过动生电动势将机械能转化为电能 。
感生电动势在电子设备和磁性材料中有着广泛的应用。例如，变压器和电感器是通过感生电动势来改 变信号和传输能量。
04
CATALOGUE
电磁制动
在某些机械设备中，利用 动生电动势可以实现电磁 制动，达到减速或停止的 目的。
电磁感应现象
动生电动势是电磁感应现 象的一种表现形式，可以 用来解释和利用电磁感应 现象。
02
CATALOGUE
感生电动势
定义与原理
定义
感生电动势是指磁场变化时在导体中产生的电动势。
原理
根据法拉第电磁感应定律，当一个导体处于变化的磁场中时，导体中的自由电子 会受到洛伦兹力的作用，从而在导体两端产生电动势。
电子感应加速器
利用感生电动势加速带电粒子。
03
CATALOGUE
比较动生和感生电动势
产生方式比较
动生电动势
是由磁场和导线的相对运动引起的。当 导线切割磁力线时，导线两端会感应出 电动势。
VS
感生电动势
是由磁场的变化引起的。当磁场发生变化 时，附近的导体中会产生感应电流和电动 势。
动生电动势和感生电动势
动生电动势和感生电动势
d d 感应电动势 N dt dt 引起磁通量变化的原因 ？
磁场恒定，导体运动
导体不动，磁场变化
P.1
1、电动势定义
I
Ek
+
-
Ek : 非静电电场强度.
Ek dl
P.2
2、感应电动势的分类： （1）动生电动势 稳恒磁场中的导体运动 , 或者回路面积 变化、取向变化等。 （2）感生电动势： 导体不动，磁场变化。
OP
P.5
动生
OP
(v B) dl
混合积：(a b ) c
× × P ×
(vB sin ) cosdl
OP
×
× × ×
×
(v × B) ×
× ×
×
特例 B均匀，杆 l水平运动：
l×
×
× v×
× B
× O ×
OP
l
l (vB sin 900 )cos00 dl (v B) dl 0
vBl
vBdl vBl
0
P.6
2、计算方法
d动生 (v B) dl
动生
×
×
× P× B × dl
× ×
OP
(v B) dl
1 2 d BL 2 dt 1 2 BL 2
×
×
× P × × × ×
× ×
B ×
×
×
×
o
×
×
×
×
×
×
×
大学物理(8.2.2)--动生电动势感生电动势
，求金
属
杆中
的
动生
电
动B 势
。O′
距 a 点为 l 处取一线元矢d量l v r l sin
b
该，处 的 非 静 电 场 场 强 为 ：
Ek
v
B
r
Ek
Ek vB lB sin
该线元运动时产生的电动势 di Ek dl
al
：di Ek dl cos(900 ) Ek dl sin lBdl sin 2
计算该线元运动时产生的电动势 di
， Ek dl
(v
B)
dl
（ 3 ）：计算该导线运动时产生的动生电动
势
εi
l
(v
B)
dl
i 0 电动势方向与积分路线方向相同 i 0 电动势方向与积分路线方向相反
例 8-3: 一长度为 L 的金属杆 ab 在均匀B磁场 中绕平行于磁
的
金属棒，金属棒绕其一端 O 顺时针匀速转动，转动角速度为
，
O 点至导线的垂直距离为 a ，
解
：金距1属)O选棒点O求所为：在l方M处处1向)的取当为金磁一金积属感线属分棒应元棒路内强矢转线d感度l量至应为与电B：v长动直2势l0导的aI 线,大方平小向行和，方如向图I；中
该，处 的 非 静 电 场 场 强 为 ：
场方向
磁场
′ 的定轴 OO′ 转动，已知杆的角速度为 ，杆相对于 的方位角为 θ ，求金属杆中的动生电动势B 。O′
b
L
a
O
例 8-3:
2.动生电动势和感生电动势
由
SB
dS可知，取决于B、S以及B与S
的夹角三个因素，我们把由于B变化而引起的感
应电动势叫做感生电动势；而把由于S或B与S
的夹角的变化而引起的感应电动势叫做动生电动势。
p
p
Fe
l e 一
B
v
i
Fm
o
o
p
L
在磁场中运动的导线内的感应电动势
上一节例题：当导线 AB以速 度 v 向右运动时，导线内每
个自由电子也就获得向右的
定向速度 ，由于导线处在
D
A
v
B l
v 磁仑场兹中力，F自为由电F子受到ev的洛B
(v
B)
dl
op
由上式可以看出，矢积
vB
与d l
成锐角时， i
为有向正正；；负i 成之为钝分负角，时时， i，则为表正i 示为时电负，动表。势示因的电此方动，向势由逆方上着向式顺算d l着出的的d方l电向动。的势方
对于闭合回路
i
(v B) dl
~
电磁阻尼
涡电流
线圈炮
轨道炮
I
B
l
涡流的危害：变压器、电机铁芯发热。
Fe
l e 一
B Fm
(e)v
B
p
i
o
Ek
Fm (e)
v
B
i
感生电动势和动生电动势
小结
感生 电动 势和 动生 电动 势 感应电场:由变化的磁场激发的电 场. 感生电动势:由感应电场产生的感 : 应电动势称为感生电动势. 动生电动势:由于导体运动而产生 的感应电动势.
5感生电动势和动生电动势
一.感应电场与感生电动势 一个闭合电路静止于磁场中,由 于磁场强弱的变化,闭合电路内 产生了感应电动势.这种情况下, 哪一种作用扮演了非静电力的 角色?
磁场Байду номын сангаас强
英国物理学家麦克斯韦在他的电磁场理论 中指出,变化的磁场会在空间激发一种电场, 这种电场对电荷会产生力的作用如果此刻 周围空间存在闭合导体,导体中自由电荷会 在这种电场力的作用下定向移动,产生感应 电流,或者说产生感应电动势.变化的的磁 场能在周围空间激发电场,这种电场叫感应 电场,由感生电场产生的感应电动势称为感 感应电动势称为感 感应电动势称为 生电动势. 生电动势
导体CD在匀强磁场B中以速度V向右运动, 并且导线CD与B.V的方向相垂直,由于正电 荷随导体一起运动,因此每个电荷受到的洛
X X X L X X X C X XF洛 X X F电 X D V
伦兹力为F洛=QVB,F洛方向向上,正 电荷向上运动,使导体下端出现负电 X , X 荷,结果上端C的电势高于下端D的 X 电势,出现由C指向D的静电场,此时 电场对正电荷的作用力是向下,与洛 伦兹力方向相反,当二力互相平衡时， ＣＤ两端便产生一个稳定的电势差，
X
可见,运动的导体CD就是一个电源,C为正极,正电
荷受到洛伦兹力的作用,从D端搬到C端,这里,洛伦 兹力就相当于电源中的非静电力,根据电动势的定 义,电动势等于单位正电荷从负极通过电源内部移 动到正极非静电力所做的功,作用在单位正电荷上 的洛伦兹力 F洛
动生电动势和感生电动势
a
注意Biblioteka r r r ε = ∫ (v × B)⋅ dl
b a
ε 是标量， （1）ε 是标量，ε > 0 时， 的方向由 a ε 到 b ，ε < 0 时， 的方向由 b 到 a ； r r r r B 的速度， （2）v 是导体线元 dl 的速度， 是 dl 所在处的磁感应强度; 所在处的磁感应强度; r r r （3）( v × B ) ⋅ dl 中有两个夹角 α 和 β ， r r r r α v 其中 v × B = vB sin α ， = 0时， × B = 0 ； r r r (v × B ) ⋅ dl = vB sin α cos βdl .
vµ0 I 0.3 ln = = −4.4 × 10− 6 ( V ) 2π 0.1
指向． 电动势的方向 B 由 A 指向．
一.感生电动势：一个静止的导体回 B 感生电动势： 当它包围的磁场发生变化时， 路，当它包围的磁场发生变化时，
L
穿过它的磁通量也会发生变化， 穿过它的磁通量也会发生变化， 这时回路也会产生感应电动势。 这时回路也会产生感应电动势。 二、感生电动势产生的原因
感生电动势 r r r r dφ m d ε = ∫ E 感 ⋅ dl = − = − ∫∫ B ⋅ dS dt dt S L r r r Q E = E 静 + E感
r r ∫ E 静 ⋅ dl = 0
L
r r r ∂B r ∫ E感 ⋅ dl = − ∫∫ ∂t ⋅ dS L S
r r r ∂B r ∫ E ⋅ dl = − ∫∫ ∂t ⋅ dS L S
r u
实例： 实例：法拉第利用一半径为 R 的铜盘在均 r 中转动， 匀磁场 B 中转动，角速度为ω ．求盘上沿半径 方向产生的感应电动势．解法见例1 方向产生的感应电动势．解法见例1．