基于Simulink的火炮伺服系统自抗扰控制仿真
计算机仿真实验-基于Simulink的伺服系统
实验八 基于Simulink 的伺服系统仿真一. 实验目的1) 熟悉Simulink 的工作环境及其SimPowerSystems 功能模块库;2) 掌握Simulink 的电力电子电路系统建模和仿真方法;3) 掌握Simulink 下数学模型的仿真方法;4)掌握PID 控制对系统输出特性的影响。
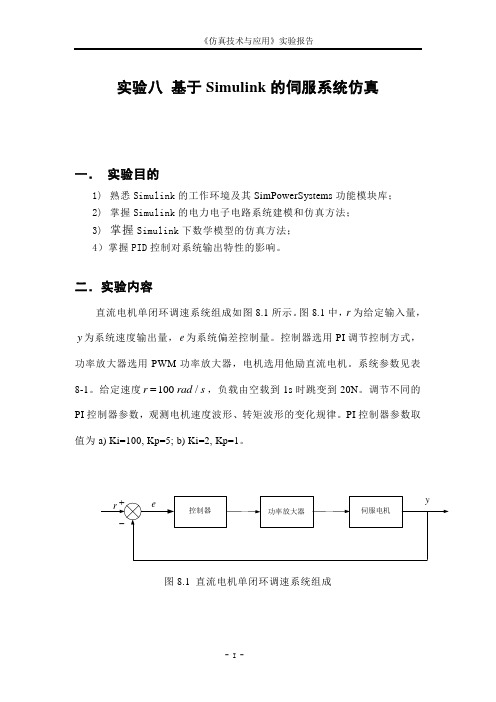
二.实验内容直流电机单闭环调速系统组成如图8.1所示。
图8.1中,r 为给定输入量,y 为系统速度输出量,e 为系统偏差控制量。
控制器选用PI 调节控制方式,功率放大器选用PWM 功率放大器,电机选用他励直流电机。
系统参数见表8-1。
给定速度100 /r rad s =,负载由空载到1s 时跳变到20N 。
调节不同的PI 控制器参数,观测电机速度波形、转矩波形的变化规律。
PI 控制器参数取值为a) Ki=100, Kp=5; b) Ki=2, Kp=1。
控制器功率放大器伺服电机r ye +-图8.1 直流电机单闭环调速系统组成三.实验步骤1. 建立电路仿真系统在Simulink仿真环境中打开Simulink库,找出相应的单元部件模型,构造图所示的仿真模型。
其中用到了直流电机模块。
直流电机模块有1个输入端子、1个输出端子和4个电气连接端子。
电气连接端子与直流电机励磁绕组相连。
A+和A-与电机电枢绕组相连。
输入端子是电机负载转矩的输入端。
输入端子(m)输出一系列的电机内部信号,由4路信号组成。
通过“信号数据流模块库”中的“信号分离”模块,即Demux模块可以将输出端子m 中的各路信号分离出来。
经过整流桥变换向电机提供直流电压。
经励磁回路,输出PWM波形。
同时,电机的转速作为反馈信号反馈到输入端。
对于三相电压源,选择频率为50Hz,幅值为2203。
按图连接好线路,设置参数,建立其仿真模型,并对各个单元部件模型的参数进行修改,如图所示。
2.进行仿真波形输出示波器的输出波形如下,依次为电机转速,电枢电流,场电流,电磁转矩(1)Ki=100, Kp=5(2)Ki=2, Kp=1四、实验结论由上图可见,此系统为脉冲比较系统,仿真模型中利用负反馈,经PI 控制输出误差给脉波发生端。
基于matlab仿真的火箭推进系统抗干扰能力最优化系统参数的研究

信实101专业10级《计算机仿真与MATLAB》课程报告题目:基于matlab仿真的火箭推进系统抗干扰能力最优化系统参数的研究班级:信实101姓名:学号:2012年12 月基于MATLAB/SIMULINK 的火箭最优化抗干扰系统的设计与分析摘要: 在火箭在发射过程中会受到干扰信号的作用而偏离轨道,故需设计出抗干扰系统来尽量减少飞行器飞行的过程中扰动因素的影响,提高系统性能,使火箭的角度通过控制系统来跟踪参考角度。
通过取不同的比例微分环节的K 值对系统进行无扰动信号的、扰动信号单独作用、扰动信号与正弦信号叠加时进行输出测试,得到与原信号拟合度最强的的K 值。
1.1 决定火箭推进系统抗干扰能力的系统参数——控制对象建模For personal use only in study and research; not for commercial use(1)被控对象的数学模型火箭推力及方向关系如图(1)所示,这里()t θ为火箭的方向与速度的夹角,()t ϕ表示火箭推进器的角度,()w t 表示加在火箭上的干扰风力。
控制器设计的目标是使火箭的角度跟踪参考角度()r t θ。
发动机可以直接控制推进器的角度并对推进器定位。
系统模型可用下面等式来表示:For personal use only in study and research; not for commercial use()()10.5()()()11s s W s s s s s Θ=Φ+--火箭推进器示意图(2)控制系统的数学模型0.5()c G s ()11s s -+-()W s ()s Φ()s Θ()r s Θ()(2)c G s K s =+控制系统的原理框图,其中()W s 为扰动信号,()1r t θ=为输入信号。
1.2 火箭最优化抗干扰推进系统原理分析 (负反馈的作用)?采用负反馈控制器,从火箭推进系统的数学模型可以看到,当有扰动信号()W s的作用时,系统通过负反馈环节1.3 火箭最优化抗干扰推进系统MATLAB仿真分析(1)MATLAB程序设计,或Simulink模型,或二者的结合(2)仿真参数的设置,思考仿真参数的影响等(3)系统特性分析,例如开环系统的时域/频域分析,加入控制器后系统的时域/频域分析等,应有仿真结果,如图、表、结果数据等。
基于SIMULINK的高炮随动系统仿真研究

基于SIMULINK的高炮随动系统仿真研究安树;陈永利【期刊名称】《测试技术学报》【年(卷),期】2010(024)006【摘要】高炮随动系统是整个高炮武器系统的核心部分, 随动系统性能的优劣将直接影响防空武器系统的整体作战效果. 为提高自行高炮武器系统的综合保障能力, 使武器系统形成最佳战斗力, 必须使随动系统性能参数满足高可靠性、高速度、高加速度等性能指标的要求. 因此研究高炮随动系统参数的选取、参数变化对系统性能的影响是非常重要的. 本文以某型高炮为例, 在分析该高炮随动系统的工作原理和控制规律的基础上, 采用 MATLAB 的动态仿真平台 SIMULINK 建立了高炮随动系统的动态模型, 并对其进行了实时仿真和分析, 从而得到了控制器的最佳参数选择. 仿真结果验证了该系统满足所给定的动静态特性的要求, 既可以指导实际系统中参数的调整, 又可以为新型火炮随动系统的设计提供可靠的参考依据.【总页数】5页(P507-511)【作者】安树;陈永利【作者单位】军械工程学院,电气工程系,河北,石家庄,050003;军械工程学院,电气工程系,河北,石家庄,050003【正文语种】中文【中图分类】TP391【相关文献】1.基于MATLAB/SIMULINK 的某型高炮伺服系统的仿真研究 [J], 齐晓慧2.基于SVPWM控制技术的高炮随动系统仿真 [J], 韦宏强;阚虎;吴红权;张鹏;郑屹;樊蓉3.基于AMESim的高炮炮闩润滑控制系统仿真研究 [J], 李献锋;房立清4.基于s函数的PMSM随动系统仿真研究 [J], 颜炳弘; 胡宏; 杜宝珠; 张捷5.基于MATLAB and Simulink的波浪能装置液压能量转换系统仿真研究 [J], 叶寅;盛松伟;乐婉贞;王坤林;张亚群因版权原因,仅展示原文概要,查看原文内容请购买。
基于simulink的高精度舰炮随动系统建模与仿真

(10)
令 Jn = i(2 Jdn + Jjn)+ Jcn,bn = i2bdn + bcn,Kn = iKdn; 则式(10)变为:
Jcn兹咬 + bn兹觶 cn + Kt(n 兹cn - im兹m)= KnIn
(11)
由式(4)可将电机的回路电压方程变为:
iCen兹觶 cn
+
InR n
+
Ln
dIn dt
Mn i
(3)
式中 Mn 为小齿轮(传动箱)和电机轴之间的弹 性力矩,Jdn 与 bdn 分别为电机的转动惯量和等效粘性 摩擦系数;Jin 为减速机的转动惯量。图中 Jin 和 Jdn 已 合成为 Jn。
(4)小齿轮(传动箱)的力学方程
小齿轮(传动箱)的转角 兹cn 和电机轴的转角 兹n 的关系为:
式中 n 表示双电机标识 1 或 2):
(1)电机电枢回路电压平衡方程[1]
Cen兹n
+
InR n
+
Ln
dIn dt
= Un
(1)
Cen 是电机的反电动势常数,In,Rn,Ln,Un 分别是
收稿日期:2019-09-19 作者简介:高文英(1979-),男,陕西宝鸡人,硕士研究生,工程师,主要从事武器装备研究。
I1 K1
1 兹咬 c1 1 兹觶 c1 1 兹c1 J1 S S
K c1
K i1
im Jms +b m
1 兹m S
1 舰炮随动系统的数学模型
K c2
K i2
传统电机随动系统模型如图 1 所示;图中 U(f s) 为随动控制电压,该控制信号控制电机输出相应控 制力矩 T(m s),带动相应负载以速度 棕(s)进行指定运 动 兹(s)。由于系统物理特性(如摩擦、齿隙),系统中 还存在扰动力矩 T(d s)。
基于Simulink的火炮伺服系统自抗扰控制仿真

收稿日期:2014⁃02⁃17
1 自抗扰控制器的原理
ADRC 是 在 非 线 性 PID 框 架 上 ,用“ 扩 张 状 态 观 测 器 ”对 扰 动 进 行 实 时 估 计 与 补 偿 构 造 出 具 有“ 自 抗 扰 功 能”的新型实用控制器 。 [4]
参数 5 100 5.25 0.24 0.000 77 0.22 0.015
反电势常数 (/ V(/ kr/min)
5.2
连续堵转电流 /A
84ቤተ መጻሕፍቲ ባይዱ
母线电压 /V
56
典型三闭环随动系统的结构框图如图 1 所示。其 中 ACR 代表电流调节器,ASR 代表速度调节器,分别采 用为 PID 控制和比例调节控制。位置环采用 ADRC 调 节 器 [10⁃ 。 11] 忽 略 摩 擦 转 矩 系 数 B。 电 机 转 速 输 出 Ωo 到 炮管角度变化量 θo 之间是传动装置。
鲁棒性。
关键词:Simulink;伺服系统;自抗扰;火炮
中图分类号:TN964⁃34
文献标识码:A
文章编号:1004⁃373X(2014)10⁃0120⁃03
Simulation of ADRC for artillery's servo system based on Simulink
GUO Jing,YANG Gang,YANG Jun,JIA Qiang
自 抗 扰 控 制 器(Active Disturbance Rejection Con⁃ troller,ADRC)是 基 于 PID 控 制 器 发 展 的 一 种 新 型 非 线 性控制器。ADRC 汲取经典 PID 的优点及现代控制理论 的控制思路方法,解决了响应快速与超调的矛盾以及现 代控制理论依赖控制对象数学模型的局限,具有广阔的 应用前景 。 [1⁃3]
基于S函数在自抗扰控制器Simulink仿真中的应用

App ia i n o f nci n i i u i i ulto o lc to fS-u to n S m l nk sm a in fADRC
MA n — u n Yo g g a g,RAN n Ni g,ZHAO e g Pn
( c ol f ot l n o p t n ier g N r h aEetcP w r nvri , adn 7 0 3 hn ) Sh o o nr dC m ue E g e n , o h C i lc o e i sy B o ig 10 ,C ia C oa r n i t n i r U e t 0
c mb n t n a d e n e t t b e v ra d i lm e ts b y t ms e c p ua i n o i a i n  ̄e d d sa e o s r e n mp e o n u s s e n a s lt .Th o g h i t a t mp r - o r u h t e ma n se m e ea
控 制 系统 的 仿 真 实 例 。 明 自抗扰 技 术 具 有 较 好 的调 节 品质 和 抗 干 扰 性 。 说
关键词 : 自抗扰控制 ;- n t n 子系统封装 ; Sf c o ; u i 仿真
中 图分 类 号 :T 3 19 T 2 3 P 9 . ; P 7 文 献标 志码 : B
自抗扰控 制器 由三个部 分组成 : 1 跟踪微分器 ( D) 为 系统 输入 安排 过渡 过程 , 到光 ) T : 得
滑的输入信号 以及 输入信号的微分信号 ;
2 扩 张状态观测器 ( S ) 估 计 出实时 作用 量 而给 予补 ) EO :
q ik e s a d h s hghp a t a au . uc n s n a i r ci l le c v Ke d ywors:ADRC;S- n t n;s b y t m a k g f ci u o u s se p c a e;smuain i lt o
自抗扰控制器在位置伺服系统中的参数整定及仿真

自抗扰控制器在位置伺服系统中的参数整定及仿真郑伟;董文妍;张焕鑫;段然;邓钊【期刊名称】《计算机测量与控制》【年(卷),期】2015(23)10【摘要】针对自抗扰控制器整定困难的问题开展研究;基于MATLAB/Simulink软件设计了自抗扰控制器,结合永磁同步电机控制系统各模块结构,实现了位置伺服系统的闭环仿真,利用仿真输出及时间、参数值绘制三维图象,通过对图象的分析验证了参数整定的新方法,实现了自抗扰控制器的参数整定;最后,通过对比自抗扰和PI 控制器在恒值、正弦、斜坡等给定输入下的跟踪效果,得出自抗扰控制器的控制效果优于PI控制器的结论.【总页数】4页(P3364-3366,3369)【作者】郑伟;董文妍;张焕鑫;段然;邓钊【作者单位】北京航天自动控制研究所宇航智能控制技术国家重点实验室,北京100854;北京机电工程研究所,北京 100074;北京航天自动控制研究所宇航智能控制技术国家重点实验室,北京100854;北京航天自动控制研究所宇航智能控制技术国家重点实验室,北京100854;北京航天自动控制研究所宇航智能控制技术国家重点实验室,北京100854【正文语种】中文【中图分类】P391【相关文献】1.用MATLAB仿真分析自抗扰控制器的整定参数 [J], 张晓东;童少为2.用MATLAB仿真分析自抗扰控制器的整定参数 [J], 张晓东;童少为3.改进遗传算法整定自抗扰控制器参数及应用 [J], 孙雨萌; 张旭秀4.基于模拟退火智能算法的自抗扰控制器参数整定及仿真 [J], 陈智华;耿修堂;肖建华;张勋才;甘作新5.PMSM伺服系统线性自抗扰控制器的参数整定 [J], 许文波;魏泽宇;孔伟;潘龙;刘伟奇因版权原因,仅展示原文概要,查看原文内容请购买。
基于Simulink对自抗扰控制技术的仿真分析

z2 − β1e = z3 − β2 fal(e,
α1
,
δ
)
+
bu
z3 = −β3 fal(e,α2,δ )
其中 fal 函数定义如下:
e
fal
(e,α
,
δ
)
δ
1−α
,
e
≤δ
e
α
sign(e),
e
>δ
控制量形成:
装后的子系统仅需调节模块参数便可以直接使用,增强了模
e=1 x1 − z1
关键词:自抗扰控制;M_function;封装;仿真 中图分类号:TP273.2 文献标识码:A 文章编号:1003-9767(2019)01-167-03
Simulation Analysis of Active Disturbance Rejection Control Technology Based on Simulink
2 自抗扰控制器的 Simulink 建模
(2) (3) (4)
TD 数学模型:
ESO 中可以利用一个 M_function 程序使用非线性函数
e0= x1 − v0
x1
=
x2
x2 = f
f
=−r × sign(e+
x2 x2 2r
)
(1)
fal(e,a,δ) 得到 z4 1,z4 2,z4 33 个微分式中的减数。其程序如下: function [y3,y2,y1] = fcn(e,B3,B2,B1) y1 = B1*e; y2 = B2*fal(e,0.5,0.01); y3 = B3*fal(e,0.25,0.01);
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于Simulink的火炮伺服系统自抗扰控制仿真
作者:郭婧杨刚杨军贾强
来源:《现代电子技术》2014年第10期
摘要:为了解决火炮伺服系统存在负载变化大、冲击扰动力矩强等问题,将自抗扰控制技术应用到火炮伺服系统位置控制器中。
该控制算法通过实时估计与补偿来弥补传统控制方法的不足。
通过在Simulink软件平台搭建了ADRC的火炮伺服系统三环模型,仿真结果对比传统PID控制。
对比结果表明,基于ADRC的系统超调小、响应速度较快、具有较强的鲁棒性。
关键词: Simulink;伺服系统;自抗扰;火炮
中图分类号: TN964⁃34 文献标识码: A 文章编号: 1004⁃373X(2014)10⁃0120⁃03
Abstract: An active disturbance rejection control (ADRC) technology is proposed for an artillery servo system with load disturbance and large disturbed moment. It is to be used in the location controller in the artillery servo system. The control method made up insufficient of the traditional control method by real⁃time estimation and compensation. Three⁃loop model (speed loop, location loop and current loop) of artillery servo system with closed⁃loop ADRC was established in the Simulink software. It was compared with the traditional PID mode control method. The simulation results show the system based on ADRC technology has the advantages of
high⁃speed response, less overshoot and strong robustness.
Keywords: Simulink; servo system; ADRC; antillery
0 引言
某火炮伺服系统是一个具有冲击力矩强、负载变化大等特点的非线性系统。
针对此类大时滞、参数变化较大的系统,传统PID控制由于响应快速和超调之间的矛盾以及参数需要实时调整等现存问题不能满足其控制精度和跟踪要求。
自抗扰控制器(Active Disturbance Rejection Controller,ADRC)是基于PID控制器发展的一种新型非线性控制器。
ADRC汲取经典PID的优点及现代控制理论的控制思路方法,解决了响应快速与超调的矛盾以及现代控制理论依赖控制对象数学模型的局限,具有广阔的应用前景[1⁃3]。
本文将自抗扰控制技术运用于某火炮位置伺服系统,基于Simulink平台进行建模。
通过仿真分析,采用自抗扰技术实现对某火炮位置伺服系统的控制,并与传统PID控制的结果进行对比分析。
1 自抗扰控制器的原理
ADRC是在非线性PID框架上,用“扩张状态观测器”对扰动进行实时估计与补偿构造出具有“自抗扰功能”的新型实用控制器[4]。
ADRC由跟踪微分器(TD)、扩张状态观测器(ESO)和非线性状态误差反馈控制律(NLSEF)三部分构成。
TD根据伺服系统的输入[θi]和承受力来安排过渡过程;ESO的作用是由控制量和被控对象的输出[θo],估计出伺服系统的状态和所受到的总的未知扰动的实时作用量;TD的输出和ESO的状态变量之间产生误差,NLSEF利用此误差用非线性组合形式产生控制量对系统进行补偿[5]。
2 控制系统的设计
2.1 控制对象
本文以某火箭炮位置伺服系统进行建模仿真研究。
按位置环、速度环、电流环三闭环调速系统对伺服系统建立模型。
对于水平调炮1 000 mil,PID控制器需要重新调整参数。
由图7可以看出:PID控制和ADRC控制也都可满足控制要求。
PID控制响应时间为10.2 s,ADRC的系统响应时间为8.5 s,ADRC速度较快,无振荡与超调。
通过以上对比仿真分析可知:采用ADRC作为控制器的系统,响应性能明显优于传统PID控制器。
以阶跃作为输入主令的ADRC算法,系统调炮误差小,系统的响应速度快,且具有较强的抗干扰能力。
因此,所设计的ADRC控制器能够满足某火炮控制系统相关要求。
5 结论
针对某火炮伺服系统,采用ADRC对其进行控制建模和仿真分析。
仿真结果表明,在同被控伺服系统并加入相同干扰的条件下,较之采用传统PID控制器的位置伺服系统,采用ADRC的火炮位置伺服系统具有更优良的性能,且无超调,对干扰等变化具有更强的鲁棒性。
参考文献
[1] 徐振辉.基于遗传算法的自抗扰炮控系统优化设计[J].计算机与现代化,2012,12(15):43⁃46.
[2] 张意,马清华.基于自抗扰控制技术的导弹控制系统设计[J]. 弹箭与制导学报,2010,32(1):37⁃40.
[3] 滕福林,胡育文.基于自抗扰控制器的交流位置伺服系统[J].电气传动,2011(11):43⁃46.
[4] 韩京清.一类不确定对象的扩张状态观测器[J].控制与决策,1995,10(1):85⁃88.
[5] 韩京清,王伟.非线性跟踪:微分器[J].系统科学与数学,1994,14(2):177⁃183.
[6] 周伟科,吕强.自抗扰控制在坦克炮控执行机构中的应用[J].火炮发射与控制学报,2009(3):18⁃21.
[7] 孙凯,许镇琳.基于自抗扰控制器的永磁同步电机位置伺服系统[J].中国电机工程学报,2007,27(15):43⁃46.。
