中考数学满分之路(二)—四点共圆
专题:四点共圆在中考数学及自主招生中的应用
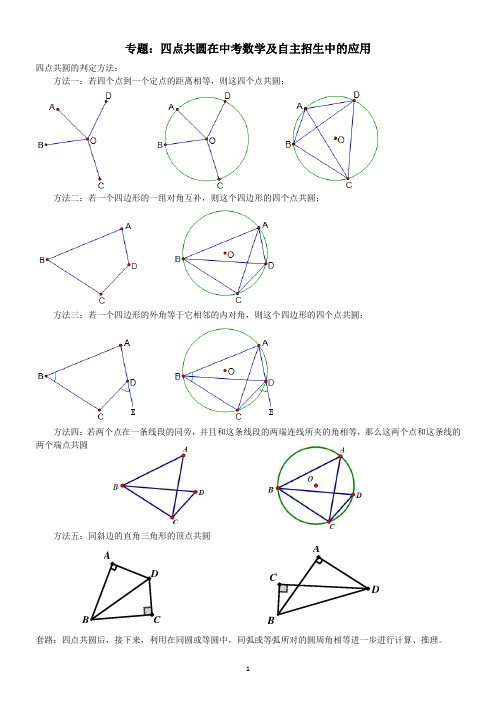
专题:四点共圆在中考数学及自主招生中的应用四点共圆的判定方法:方法一:若四个点到一个定点的距离相等,则这四个点共圆;方法二:若一个四边形的一组对角互补,则这个四边形的四个点共圆;方法三:若一个四边形的外角等于它相邻的内对角,则这个四边形的四个点共圆;方法四:若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆方法五:同斜边的直角三角形的顶点共圆C AD B C A D经典例题题型1、先证四点共圆后,然后求线段最值问题(关键是找到动点的轨迹)例1、如图1,OA=OB=4,∠OCA=135°(1)求证:AC⊥BC;(2)如图2,点P与点B关于x轴对称,试求PC的最小值。
题型2、先证四点共圆后,然后求角度、三角函数值、或线段的比值(若从一个点出发的三条线段之间的比值问题,特别注意三弦定理)例2、如图,抛物线y=ax2-4ax+b与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为M,直线y=x-3经过M,B两点,交y轴于点D(1)求抛物线的解析式;(2)设P为x轴上一动点,过P作PC的垂线交直线BD于Q,连接CQ,求∠PQC的度数例3、(2013年哈尔滨)如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为例4、(2013•绍兴)在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD.(2)如图2,AC:AB=1:,EF⊥CE,求EF:EG的值.例5、如图1,直线y=−21x+2交x 轴、y 轴于A 、B 两点,C 为直线AB 上第二象限内一点,且S △AOC =8,双曲线 y=xk (x <0)经过点C (1)求k 的值; (2) 如图2,Q 为双曲线上另一点,连接OQ ,过C 作CM ⊥OQ 于M ,CN ⊥y 轴于N ,连接MN 。
初三 关于圆 四点共圆
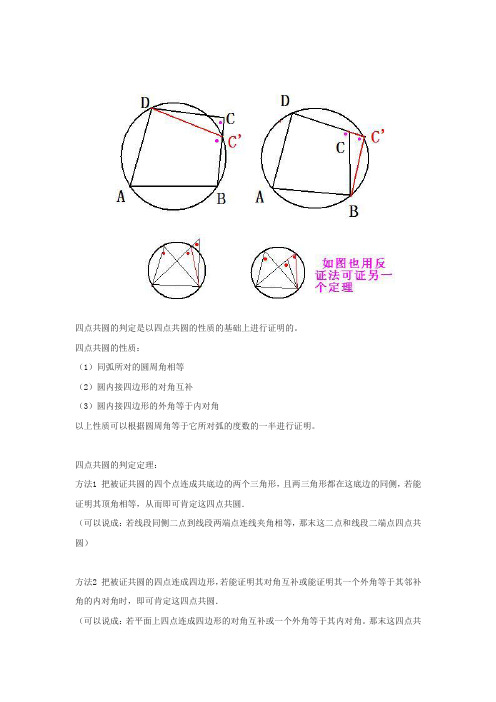
四点共圆的判定是以四点共圆的性质的基础上进行证明的。
四点共圆的性质:
(1)同弧所对的圆周角相等
(2)圆内接四边形的对角互补
(3)圆内接四边形的外角等于内对角
以上性质可以根据圆周角等于它所对弧的度数的一半进行证明。
四点共圆的判定定理:
方法1 把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等,从而即可肯定这四点共圆.
(可以说成:若线段同侧二点到线段两端点连线夹角相等,那末这二点和线段二端点四点共圆)
方法2 把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆.
(可以说成:若平面上四点连成四边形的对角互补或一个外角等于其内对角。
那末这四点共
圆)
我们可都可以用数学中的一种方法;反证法开进行证明。
现就“若平面上四点连成四边形的对角互补。
那末这四点共圆”证明如下(其它画个证明图如后)
已知:四边形ABCD中,∠A+∠C=180°
求证:四边形ABCD内接于一个圆(A,B,C,D四点共圆)
证明:用反证法
过A,B,D作圆O,假设C不在圆O上,刚C在圆外或圆内,
若C在圆外,设BC交圆O于C’,连结DC’,根据圆内接四边形的性质得∠A+∠DC’B=180°,∵∠A+∠C=180°∴∠DC’B=∠C
这与三角形外角定理矛盾,故C不可能在圆外。
类似地可证C不可能在圆内。
∴C在圆O上,也即A,B,C,D四点共圆。
四点共圆(精华)

四点共圆(限量版)板块一:辅助圆思想平面几何中有很多题中的背景并没出现圆,但是在解题过程中我们会发现,如果能够适当添加辅助圆,不仅能让题目瞬间变得简单,同时还可能会有意想不到的收获,得到很多有趣的结论,而且纵观这几年中考命题趋势,第24题的几何综合题越来越需要我们有辅助圆的思想和思维了,而辅助圆思想又是学习四点共圆的基础.构造辅助圆的基本思路:1、共顶点,等线段想辅助圆(圆的定义);2、不共线的三点确定一个圆(即做这个三角形的外接圆);3、利用四点共圆的判定作辅助圆.1、如图,在四边形ABCD中,AB=AC=AD,∠BCD=150°,求∠BAD的度数.DCBA2、(大兴期末)已知四边形ABCD,A B∥CD,且AB=AC=AD=a,BC=b,且2a>b求cos DBA∠的值.3、(2014年海淀一模)在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为α,且0180α<<,连接AD、BD.(1)如图1,当∠BAC=100°,60α=时,∠CBD 的大小为_________;(2)如图2,当∠BAC=100°,20α=时,求∠CBD的大小;(3)已知∠BAC的大小为m(60120m<<),若∠CBD的大小与(2)中的结果相同,请直接写出α的大小.图2DCBA图1AB C4、(2011海淀期末)如图,E ,B ,A ,F 四点共线,点D 是正三角形ABC 的边AC 的中点, 点P 是直线AB 上异于A ,B 的一个动点,且满足30CPD ∠=︒,则( )A .点P 一定在射线BE 上B .点P 一定在线段AB 上C .点P 可以在射线AF 上 ,也可以在线段AB 上D .点P 可以在射线BE 上 ,也可以在线段5、(2011西城一模)平面直角坐标系xOy 中,抛物线244y ax ax a c=-++与x轴交于点A 、点B , 与y 轴的正半轴交于点C ,点 A 的坐标为(1, 0),OB =OC , 抛物线的顶点为D . (1) 求此抛物线的解析式;(2) 若此抛物线的对称轴上的点P 满足∠APB =∠ACB ,求点P 的坐标;(3) Q 为线段BD 上一点,点A 关于∠AQB 的平分线的对称点为A ',若2=-QB QA 求点Q 的坐标和此时△QAA '的面积.C6、(2013海淀期中)初三(1)班的同学们在解题过程中,发现了几种利用尺规作一个角的半角的方法.题目:在△ABC中,80ACB∠=︒,求作:40ADB∠=︒.图1 图2仿照他们的做法,利用尺规作图解决下列问题,要求保留作图痕迹.(1)请在图1和图2中分别出作20APB∠=︒;(2)当60ACB∠=︒时,在图3中作出30APB∠=︒,且使点P在直线l上.lACBDACB EA B板块二:四点共圆判定:1、到一定点的距离相等的四个点共圆(圆的定义) 2、共斜边的直角三角形的顶点共圆 (圆的定义)(此判定考察最多)3、同底且同侧张角相等的两个三角形的顶点共圆 (同弧所对圆周角相等逆定理)4、对角互补或有一个外角等于其内对角的四边形的顶点共圆(圆内接四边形逆定理)另注:四点共圆的判定还有很多,我们只讲中考中涉及到的这四种,其实基本上所有的圆幂 定理的逆定理都可以判定四点共圆,比如相交弦定理,切割线定理及推论,托勒密定 理等.有兴趣的同学等暑假我们再讲.用途:圆中的性质很多,知道四点共圆后,我们可以利用其性质去解决一些几何证明题,判 断动点轨迹题及动点最值问题等,就会显得山穷水尽疑无路,柳暗花明又一村.7、证明判定3和4的成立(反证法)8、(海淀)已知:AOB △中,2AB OB ==,COD △中,3CD OC ==,ABO DCO =∠∠.连接AD 、BC ,点M 、N 、P 分别为OA 、OD 、BC 的中点.图1 (1) 如图1,若A 、O 、C 三点在同一直线上,且60ABO =∠,则PMN △的形状是________________,此时ADBC=________; (2) 如图2,若A 、O 、C 三点在同一直线上,且2ABO α=∠,证明PMN BAO △∽△,并计算ADBC的值(用含α的式子表示); (3) 在图2中,固定AOB △,将COD △绕点O 旋转,直接写出PM 的最大值.9(海淀)如图一,在△ABC 中,分别以AB ,AC 为直径在△ABC 外作半圆1O 和半圆2O ,其中1O 和2O 分别为两个半圆的圆心. F 是边BC 的中点,点D 和点E 分别为两个半圆圆弧的中点.(1)连结1122,,,,,O F O D DF O F O E EF ,证明:12DO F FO E △≌△;(2)如图二,过点A 分别作半圆1O 和半圆2O 的切线,交BD 的延长线和CE 的延长线于点P 和点Q ,连结PQ ,若∠ACB =90°,DB =5,CE =3,求线段PQ 的长;(3)如图三,过点A 作半圆2O 的切线,交CE 的延长线于点Q ,过点Q 作直线F A 的垂线,交BD 的延长线于点P ,连结P A . 证明:P A 是半圆1O 的切线.图一A B CDE1O 2O 2O 1O AE B DP图二AB CEFDPQ1O 2O 图三10、(海淀期末) 如图,以(0,1)G 为圆心,半径为2的圆与x 轴交于A 、B 两点,与y 轴交于C 、D 两点,点E 为⊙G 上一动点,CF AE ⊥于F .当点E 从点B 出发顺时针运动到点D 时,点F 所经过的路径长为( ) A . 32π B .33π C .34π D .36π11、(2014年房山一模) 将等腰Rt △ABC 和等腰Rt △ADE 按图1方式放置,∠A=90°, AD 边与AB 边重合, AB =2AD =4.将△ADE 绕点A 逆时针方向旋转一个角度α(0°≤α≤180°),BD 的延长线交直线CE 于点P .(1)如图2,BD 与CE 的数量关系是 , 位置关系是 ; (2)在旋转的过程中,当AD ⊥BD 时,求出CP 的长; (3)在此旋转过程中,求点P 运动的路线长.12、(2012朝阳)在矩形ABCD 中,点P 在AD 上,AB =2,AP =1,将三角板的直角顶点放在点P 处,三角板的两直角边分别能与AB 、BC 边相交于点E 、F ,连接EF . (1)如图,当点E 与点B 重合时,点F 恰好与点C 重合,求此时PC 的长;(2)将三角板从(1)中的位置开始,绕点P 顺时针旋转,当点E 与点A 重合时停止,在这个过程中,请你观察、探究并解答:① ∠PEF 的大小是否发生变化?请说明理由;② 直接写出从开始到停止,线段EF 的中点所经过的路线长.(0,1)I 图1图2DB EB ABA备用图D F A B E13、(2015北京四中12月月考)如图,在边长为2的菱形ABCD 中,∠A =60°,M是AD 边的中点,N 是AB 边上一动点,将△AMN 沿MN 所在的直线翻折得到△A'MN ,连接A'C ,则A'C 长度的最小值是_______.14、(2013昌平一模)在△ABC 中,AB =4,BC =6,∠ACB =30°,将△ABC 绕点B 按逆时针方向旋转,得到△A 1BC 1.(1)如图1,当点C 1在线段CA 的延长线上时,求∠CC 1A 1的度数; (2)如图2,连接AA 1,CC 1.若△CBC 1的面积为3,求△ABA 1的面积;(3)如图3,点E 为线段AB 中点,点P 是线段AC 上的动点,在△ABC 绕点B 按逆时针方向旋转的过程中,点P 的对应点是点P 1,直接写出线段EP 1长度的最大值与最小值.C 1C BA 1A图2A 1C 1ABC图1图3PP 1E A 1A C 115、(2013通州期末)在平面直角坐标系xOy 中,点B (0,3),点C 是x 轴正半轴上一点,连结BC ,过点C 作直线CP ∥y 轴. (1)若含45°角的直角三角形如图所示放置.其中,一个顶点与点O 重合,直角顶点D在线段BC 上,另一个顶点E 在CP 上.求点C 的坐标; (2)若含30°角的直角三角形一个顶点与点O 重合,直角顶点D 在线段BC 上,另一个顶点E 在CP 上,求点C 的坐标.备用图备用图第24题图。
中考数学总复习《四点共圆问题》专题(含答案)

如图,在 中, , 中, ,若 三点在同一直线 上. 连接 、 ,点 、 、 分别为 、 、 的中点.求证 .
在梯形ABCD中, , , , 分别在 , 上, .
求证: .
如图 和 中, ,求证点 , , , 四点在同一个圆上.
(1)当点 在 内时,延长 交 于 ,连结 ,则有
如图,在△ABC中,分别以AB,AC为直径在 ABC外作半圆 和半圆 ,其中 和 分别为两个半圆的圆心.F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.过点A作半圆 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA.
求证:PA是半圆 的切线.
如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点E,且DE=2EB,F为AC的中点.
求证:(1)∠FBD=30°;(2)AD=DC.
四点共圆问题答案解析
一、解答题
(1)∵ ,∴ ,
∴ ,∴ 四点共圆.
(2) 连结 ,设 相交于
由(1)可知 是圆的直径,
又∵ 是平行四边形,∴ 是 中点,
∴ 是圆心,∴ ,
∵ ,∴ .
取 的中点 ,连接 ,故
【解析】取斜边中点,利用斜边中线等于斜边长一半,然后利用证明方法一.
∵ 是 的切线,∴ ,
∴ ,
∵ ,
∴ ,
∴ 四点共圆,
∵ ,∴ .
连结ห้องสมุดไป่ตู้,
∵ ,
∴ ,
∴ ,
∵ ,
∴ 四点共圆, 四点共圆,
∴ 五点共圆,
∴ .
2024年中考数学重难点《几何最值问题》题型及答案解析

重难点几何最值问题中考数学中《几何最值问题》部分主要考向分为五类:一、将军饮马类最值二、动点辅助圆类最值三、四点共圆类最值四、瓜豆原理类最值五、胡不归类最值几何最值问题虽然在中考数学中经常考察的是将军饮马类和辅助圆类,剩余几种虽然不经常考察,但是考到的时候难度都比较大,所以也需要理解并掌握不同类型的几何最值问题的处理办法,这样到考到的时候才能有捷径应对。
考向一:将军饮马类最值一动”“两定异侧普通一动”“两定同侧普通动”两定“一动”两定“两两动”“两定同侧两动”“两定异侧满分技巧将军饮马:。
1.(2023•绥化)如图,△ABC是边长为6的等边三角形,点E为高BD上的动点.连接CE,将CE绕点C 顺时针旋转60°得到CF.连接AF,EF,DF,则△CDF周长的最小值是3+3.【分析】分析已知,可证明△BCE≌△ACF,得∠CAF=∠CBE=30°,可知点F在△ABC外,使∠CAF =30°的射线AF上,根据将军饮马型,求得DF+CF的最小值便可求得本题结果.【解答】解:∵△ABC是等边三角形,∴AC=BC=6,∠ABC=∠BCA=60°,∵∠ECF=60°,∴∠BCE=60°﹣∠ECA=∠ACF,∵CE=CF,∴△BCE≌△ACF(SAS),∴∠CAF=∠CBE,∵△ABC是等边三角形,BD是高,∴∠CBE=∠ABC=30°,CD=AC=3,过C点作CG⊥AF,交AF的延长线于点G,延长CG到H,使得GH=CG,连接AH,DH,DH与AG 交于点I,连接CI,FH,则∠ACG=60°,CG=GH=AC=3,∴CH=AC=6,∴△ACH为等边三角形,∴DH=CD•tan60°=,AG垂直平分CH,∴CI=HI,CF=FH,∴CI+DI=HI+DI=DH=3,CF+DF=HF+DF≥DH,∴当F与I重合时,即D、F、H三点共线时,CF+DF的值最小为:CF+DF=DH=3,∴△CDF的周长的最小值为3+3.故答案为:3+3.2.(2023•德州)如图,在四边形ABCD中,∠A=90°,AD∥BC,AB=3,BC=4,点E在AB上,且AE=1.F,G为边AD上的两个动点,且FG=1.当四边形CGFE的周长最小时,CG的长为.【分析】先确定FG和EC的长为确定的值,得到四边形CGFE的周长最小时,即为CG+EF最小时,平移CG到C'F,作点E关于AD对称点E',连接E'C'交AD于点G',得到CG+EF最小时,点G与G'重合,再利用平行线分线段成比例求出C'G'长即可.【解答】解:∵∠A=90°,AD∥BC,∴∠B=90°,∵AB=3,BC=4,AE=1,∴BE=AB﹣AE=3﹣1=2,在Rt△EBC中,由勾股定理,得EC===,∵FG=1,∴四边形CGFE的周长=CG+FG+EF+EC=CG+EF+1+,∴四边形CGFE的周长最小时,只要CG+EF最小即可.过点F作FC'∥GC交BC于点C',延长BA到E',使AE'=AE=1,连接E'F,E'C',E'C'交AD于点G',可得AD垂直平分E'E,∴E'F=EF,∵AD∥BC,∴C'F=CG,CC'=FG=1,∴CG+EF=C'F+E'F≥E'C',即CG+EF最小时,CG=C'G',∵E'B=AB+AE'=3+1=4,BC'=BC﹣CC'=4﹣1=3,由勾股定理,得E'C'===5,∵AG'∥BC',∴=,即=,解得C'G'=,即四边形CGFE的周长最小时,CG的长为.故答案为:.考向二:动点辅助圆类最值满分技巧动点运动轨迹为辅助圆的三种类型:一.定义法——若一动点到定点的距离恒等于固定长,则该点的运动轨迹为以定点为圆心,定长为半径的圆(或圆弧)二.定边对直角模型原理:直径所对的圆周角是直角思路构造:若一条定边所对的“动角”始终为直角,则直角顶点运动轨迹是以该定边为直径的圆(或圆弧)三.定边对定角模型原理:在同圆或等圆中,同弧所对的圆周角相等思路构造:若一条定边所对的“动角”始终为定角,则该定角顶点运动轨迹是以该定角为圆周角,该定边为弦的圆(或圆弧)1.(2023•徐州)如图,在Rt△ABC中,∠C=90°,CA=CB=3,点D在边BC上.将△ACD沿AD折叠,使点C落在点C′处,连接BC′,则BC′的最小值为.【分析】由折叠性质可知AC=AC'=3,然后根据三角形的三边不等关系可进行求解.【解答】解:∵∠C=90°,CA=CB=3,∴,由折叠的性质可知AC=AC'=3,∵BC'≥AB﹣AC',∴当A、C′、B三点在同一条直线时,BC'取最小值,最小值即为,故答案为.2.(2023•黑龙江)如图,在Rt△ACB中,∠BAC=30°,CB=2,点E是斜边AB的中点,把Rt△ABC绕点A顺时针旋转,得Rt△AFD,点C,点B旋转后的对应点分别是点D,点F,连接CF,EF,CE,在旋转的过程中,△CEF面积的最大值是4+.【分析】线段CE为定值,点F到CE距离最大时,△CEF的面积最大,画出图形,即可求出答案.【解答】解:∵线段CE为定值,∴点F到CE的距离最大时,△CEF的面积有最大值.在Rt△ACB中,∠BAC=30°,E是AB的中点,∴AB=2BC=4,CE=AE=AB=2,AC=AB•cos30°=2,∴∠ECA=∠BAC=30°,过点A作AG⊥CE交CE的延长线于点G,∴AG=AC=,∵点F在以A为圆心,AB长为半径的圆上,∴AF=AB=4,∴点F到CE的距离最大值为4+,∴,故答案为:.3.(2023•大庆模拟)如图,AB是⊙O的直径,AB=4,C为的三等分点(更靠近A点),点P是⊙O上个动点,取弦AP的中点D,则线段CD的最大值为()A.2B.C.D.【分析】如图,连接OD,OC,首先证明点D的运动轨迹为以AO为直径的⊙K,连接CK,当点D在CK的延长线上时,CD的值最大,利用勾股定理求出CK即可解决问题.【解答】解:如图,连接OD,OC,∵AD=DP,∴OD⊥P A,∴∠ADO=90°,∴点D的运动轨迹为以AO为直径的⊙K,连接CK,AC,当点D在CK的延长线上时,CD的值最大,∵C为的三等分点,∴∠AOC=60°,∴△AOC是等边三角形,∴CK⊥OA,在Rt△OCK中,∵∠COA=60°,OC=2,OK=1,∴CK==,∵DK=OA=1,∴CD=+1,∴CD的最大值为+1,故选:D.考向三:四点共圆类最值满分技巧对角互补的四边形必有四点共圆,即辅助圆产生模型原理:圆内接四边形对角互补∴FD=,在四边形ACBF中,∠ACB=∠AFB=90°,∴A、C、B、F四点共圆,∴∠ACF=∠ABF=45°,∠CAB=∠CFB,∵∠PCD=45°∴∠ACP=∠FCD,又∵△ABE∽△FBD,∴∠BAE=∠BFD,∴∠CAP=∠CFD,∴△CAP∽△CFD,∴,在四边形ACBF中,由对角互补模型得AC+CB=,∴CF=∴,∴AP=1,∴PE=2,故答案为:2考向四:瓜豆原理类最值满分技巧瓜豆原理的特征和结论:∴AB=CD=6,∠B=∠BCD=90°,∵∠BET=∠FEG=45°,∴∠BEF=∠TEG,∵EB=ET,EF=EG,∴△EBF≌△ETG(SAS),∴∠B=∠ETG=90°,∴点G在射线TG上运动,∴当CG⊥TG时,CG的值最小,∵BC=,BE=,CD=6,∴CE=CD=6,∴∠CED=∠BET=45°,∴∠TEJ=90°=∠ETG=∠JGT=90°,∴四边形ETGJ是矩形,∴DE∥GT,GJ=TE=BE=,∴CJ⊥DE,∴JE=JD,∴CJ=DE=3,∴CG=CJ+GJ=+3,∴CG的最小值为+3,故答案为:+3.2.(2023•宿城区二模)如图,矩形ABCD中,AD=6,DC=8,点E为对角线AC上一动点,BE⊥BF,,BG⊥EF于点G,连接CG,当CG最小时,CE的长为.【分析】过点B作BP⊥AC于点P,连接PG,则可得△ABE∽△PBG,进而可知∠BPG为定值,因此CG⊥PG时,CG最小,通过设元利用三角函数和相似比可表示出PG、CP,即可求出结果.【解答】解:如图,过点B作BP⊥AC于点P,连接PG,∵,∠ABC=∠EBF,∴△ABC∽△EBF,∴∠CAB=∠FEB,∵∠APB=∠EGB=90°,∴△ABP∽△EBG,∴=,∠ABP=∠EBG,∴∠ABE=∠PBG,∴△ABE∽△PBG,∴∠BPG=∠BAE,即在点E的运动过程中,∠BPG的大小不变且等于∠BAC,∴当CG⊥PG时,CG最小,设此时AE=x,∵,∴PG=,∵CG⊥PG,∴∠PCG=∠BPG=∠BAC,∴,代入PG=,解得CP=x,∵CP=BC•sin∠CBP=BC•sin∠BAC=,∴x=,∴AE=∴CE=,故答案为:.考向五:胡不归类最值满分技巧胡不归模型解决步骤:模型具体化:如图,已知两定点A、B,在定直线BC上找一点P,使从B走道P,再从P走到A的总时间最小解决步骤:由系数k·PB确定分割线为PBPA在分割线一侧,在分割线PB另一侧依定点B构α角,使sinα=k,α角另一边为BD过点P作PQ⊥BD,转化kPB=PQ过定点A作AH⊥BD,转化(PA+k·PB)min=AH,再依“勾股法”求AH的长即可。
中考复习四点共圆

四点共圆四点共圆的判定(一)判定方法1、若四个点到一个定点的距离相等,则这四个点共圆。
2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆。
3、若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆。
4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆。
5、同斜边的直角三角形的顶点共圆。
6、若AB、CD两线段相交于P点,且PA×PB=PC×PD,则A、B、C、D四点共圆(相交弦定理的逆定理)。
7、若AB、CD两线段延长后相交于P。
且PA×PB=PC×PD,则A、B、C、D四点共圆(割线定理)。
8、若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆(托勒密定理的逆定理。
(二)证明1、若四个点到一个定点的距离相等,则这四个点共圆。
若可以判断出OA=OB=OC=OD,则A、B、C、D四点在以O为圆心OA为半径的圆上。
2、若一个四边形的一组对角互补(和为180°),则这个四边形的四个点共圆。
若∠A+∠C=180°或∠B+∠D=180°,则点A、B、C、D四点共圆。
3、若一个四边形的外角等于它的内对角,则这个四边形的四个点共圆。
若∠B=∠CDE,则A、B、C、D四点共圆证法同上。
4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆。
若∠A=∠D或∠ABD=∠ACD,则A、B、C、D四点共圆。
5、同斜边的直角三角形的顶点共圆。
如图2,若∠A=∠C=90°,则A、B、C、D四点共圆。
ADCC6、若AB、CD两线段相交于P点,且PA×PB=PC×PD,则A、B、C、D四点共圆(相交弦定理的逆定理)。
7、若AB、CD两线段延长后相交于P。
且PA×PB=PC×PD,则A、B、C、D四点共圆(割线定理)。
中考数学专题复习 四点共圆模型 含答案
共圆模型模型1共端点,等线段模型如图①,出现“共端点,等线段”时,可利用圆定义构造辅助圆.如图②,若OA=OB=OC,则A、B、C三点在以O为圆心,OA为半径的圆上.如图③,常见结论有:∠ACB=12∠AOB,∠BAC=12∠BOC.模型分析∵OA=OB=OC.∴A、B、C三点到点O的距离相等.∴A、B、C三点在以O为圆心,OA为半径的圆上.∵∠ACB是»AB的圆周角,∠AOB是»AB的圆心角,∴∠ACB=12∠AOB.同理可证∠BAC=12∠BOC.(1)若有共端点的三条线段,可考虑构造辅助圆.(2)构造辅助圆是方便利用圆的性质快速解决角度问题.模型实例如图,△ABC和△ACD都是等腰三角形,AB=AC,AC=AD,连接BD.求证:∠1+∠2=90°.证明证法一:如图①,∵AB=AC=AD.∴B、C、D在以A为圆心,AB为半径的⊙A上.∴∠ABC=∠2.在△BAC中,∵∠BAC+∠ABC+∠2=180°,∴2∠1+2∠2=180°.∴∠1+∠2=90°.证法二:如图②,∵AB=AC=AD.∴∠BAC=2∠1.∵AB=AC,∴B、C、D在以A为圆心,AB为半径的⊙O上.延长BA与圆A相交于E,连接CE.∴∠E=∠1.(同弧所对的圆周角相等.)∵AE=AC,∴∠E=∠ACE.∵BE为⊙A的直径,∴∠BCE=90°.∴∠2+∠ACE=90°.∴∠1+∠2=90°.小猿热搜1.如图,△ABC为等腰三角形,AB=AC,在△ABC的外侧作直线AP,点B与点D关于AP轴对称,连接BD、CD,CD与AP交于点E.求证:∠1=∠2.证明∵A、D关于AP轴对称,∴AP是BD的垂直平分线.∴AD=AB,ED=EB.又∵AB=AC.∴C、B、D在以A为圆心,AB为半径的圆上.∵ED=EB,∴∠EDB=∠EBD.∴∠2=2∠EDB.又∵∠1=2∠CDB.∴∠1=∠2.2.己知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b,求BD的长.解答以A为圆心,以a为半径作圆,延长BA交⊙A于E点,连接ED.∵AB∥CD,∴∠CAB=∠DCA,∠DAE=∠CDA. ∵AC=AD,∴∠DCA=∠CDA. ∴∠DAE=∠CAB.在△CAB和△DAE中.∴△CAB≌△DAE.∴ED=BC=b∵BE是直径,∴∠EDB=90°.在Rt△EDB中,ED=b,BE=2a,∴BD模型2 直角三角形共斜边模型模型分析如图①、②,Rt△ABC和Rt△ABD共斜边,取AB中点O,根据直角三角形斜边中线等于斜边一半,可得:OC=OD=OA=OB,∴A、B、C、D四点共圆.(1)共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆;(2)四点共圆后可以根据圆周角定理得到角度相等,完成角度等量关系的转化,是证明角度相等重要的途径之一.模型实例例1如图,AD、BE、CF为△ABC的三条高,H为垂线,问:(1)图中有多少组四点共圆?(2)求证:∠ADF=∠ADE.解答(1)6组①C、D、H、E四点共圆,圆心在CH的中点处;②D、B、F、H四点共圆,圆心在BH的中点处;③A、E、H、F四点共圆,圆心在AH的中点处;④C、B、F、E四点共圆,圆心在BC的中点处;⑤B、A、E、D四点共圆,圆心在AB的中点处;⑥C、D、F、A四点共圆,圆心在AC的中点处.(2)如图,由B、D、H、F四点共圆,得∠ADF=∠1.同理:由A、B、D、E四点共圆,得∠ADE=∠1.∴∠ADF=∠ADE.例2如图,E是正方形ABCD的边AB上的一点,过点E作DE的垂线交∠ABC的外角平分线于点F,求证:FE=DE.解答如图,连接DB、DF.∵四边形ABCD是正方形,且BF是∠CBA的外角平分线,∴∠CBF=45°,∠DBC=45°,∴∠DBF=90°.又∵∠DEF=90°,∴D、E、B、F四点共圆.∴∠DFE=∠DBE=45°(同弧所对的圆周角相等).∴△DEF是等腰直角三角形.∴FE=DE.P1.如图,锐角△ABC中,BC.CE是高线,DG⊥CE于G,EF⊥BD于F,求证:FG BC证明:由于Rt△BCE与Rt△BCD共斜边BC,∴B、C、D、E四点共圆.∴∠DBC=∠DEG,同理,Rt∠EDF与Rt△DGE共斜边DE,∴D、E、F、G四点共圆.于是∠DEG=∠DFG,因此,∠DBC=∠DFG.于是FG∥BC2. 如图,BE.CF为△ABC的高,且交于点H,连接AH并延长交于BC于点D,求证:AD⊥BC.3.如图,等边△PQR内接于正方形ABCD,其中点P,Q,R分别在边AD,AB,DC上,M是QR的中点.求证:不论等边△PQR怎样运动,点M为不动点.4.如图,已知△ABC中,AH是高,AT是角平分线,且TD⊥AB,TE⊥AC.求证:∠AHD=∠AHE.证明:(1)∵∠ADT=∠AHT=∠AET=90°,∴D,E,H在以AT为直径的圆上,∴∠AHD=∠ATD,∠AHE=∠ATE,又∵AT是角平分线,TD⊥AB,TE⊥AC,∴∠ATD=∠ATE,∴∠AHD=∠AHE.补充:。
中考数学冲刺——四点共圆(学生版+解析版)
中考数学冲刺——四点共圆【知识点】1、四点共圆:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
四点共圆有三个性质:(1)共圆的四个点所连成同侧共底的两个三角形的顶角相等;(2)圆内接四边形的对角互补;(3)圆内接四边形的外角等于内对角。
2、判定定理:方法1:若线段同侧二点到线段两端点连线夹角相等,那么这二点和线段二端点四点共圆。
方法2 :若平面上四点连成四边形的对角互补或一个外角等于其内对角,那么这四点共圆。
【例1】 如图,在Rt ABC △中,90ACB ∠=,3BC =,4AC =,点P 为平面内一点,且CPB A ∠=∠,过C 作CQ CP ⊥交PB 的延长线于点Q ,则CQ 的最大值为( )A .175B .154C .5D .5【例2】 如图,AB 是Rt ABC 和Rt ABD △的公共斜边,AC=BC ,32BAD ∠=,E 是AB 的中点,联结DE 、CE 、CD ,那么ECD ∠=___________________.【例3】 如图,正方形ABCD 中,9AB =,点E 为AD 上一点,且:1:2AE ED =,点P 为边AB 上一动点,连接PE ,过点E 作EF PE ⊥,交射线BC 于点F ,连接PF ,点M 为PF 中点,连接DM ,则DM 的最小值为________.【例4】 如图,等腰Rt△ABC 中,∠ACB=90°,D 为BC 边上一点,连接AD .(1)如图1,作BE⊥AD 延长线于E ,连接CE ,求证:∠AEC=45°;(2)如图2,P 为AD 上一点,且∠BPD=45°,连接CP .若AP =2,求△APC 的面积;【例5】在边长为12cm的正方形ABCD中,点E从点D出发,沿边DC以1cm/s的速度向点C运动,同时,点F从点C出发,沿边CB以1cm/s的速度向点B运动,当点E达到点C时,两点同时停止运动,连接AE、DF交于点P,设点E.F运动时间为t秒.回答下列问题:(1)如图1,当t为多少时,EF的长等于(2)如图2,在点E、F运动过程中,①求证:点A、B、F、P在同一个圆(⊙O)上;②是否存在这样的t值,使得问题①中的⊙O与正方形ABCD的一边相切?若存在,求出t值;若不存在,请说明理由;③请直接写出问题①中,圆心O的运动的路径长为_________.【例6】如图,等腰三角形△ABC中,∠BAC=120°,AB=3.(1)求BC的长.(2)如图,点D在CA的延长线上,DE⊥AB于E,DF⊥BC于F,连EF.求EF的最小值.【例7】 已知AD 为锐角ABC ∆的高,G 为AC 中点,DE AB ⊥于点E ,延长ED 至F ,使得GF GD =.(1)证明:AED AFC ∆∆;(2)证明:22AE CF BE AF ⋅=⋅;(3)若6,7,8AB BC CA ===,求四边形ACFD 的面积.A两点.【例8】如图1,抛物线2=++经过原点(0,0),(12,0)y bx c(1)求b的值;(2)如图2,点P是第一象限内抛物线2=++上一点,连接PO,若tan POA∠=,求y bx c点P的坐标;=,连接(3)如图3,在(2)的条件下,过点P的直线y m=+与x轴交于点F,作CF OFOC交抛物线于点Q,点B在线段OF上,连接CP、CB、PB,PB交CF于点E,若∠=∠,求点Q的坐标.BEF BCF∠=∠,22PBA PCB中考数学冲刺——四点共圆【知识点】1、四点共圆:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
初三数学联赛辅导 四点共圆
四点共圆四点共圆的判定方法:(1)先证三点共圆,再证第四点也在此圆上 (2)若干个点到某定点距离相等,则这些点共圆 (3)同底同侧张等角的三角形,各顶点共圆(4)若一个四边形的一组对角互补,则它的四个顶点共圆。
(5)若四边形ABCD 的对角线相交于P ,且PD PB PC PA ∙=∙,则它的四个顶点共圆。
(6)若四边形ABCD 的一组对边AB 、CD 相交于P ,且PD PC PB PA ∙=∙,则它的四个顶点共圆。
(7)(托勒密定理的逆定理)若四边形ABCD 中,BC AD CD AB BD AC ⋅+⋅=⋅ 则A 、B 、C 、D 四点共圆 (8)(西姆松定理的逆定理)从ABC ∆外一点D 引三边BC 、AB 、AC 所在直线的垂线,垂足为L 、M 、N ,若L 、M 、N 共线,则A 、B 、C 、D 四点共圆例1 如图,ABC ∆三边上的高交于H ,H 不于任一顶点重合,则以A 、B 、C 、D 、E 、F 、H 中某四个点可以确定的圆共有多少个?例2 给出锐角ABC ∆,以AB 为直径的圆与AB 边的高1CC 及其延长线交于M 、N ,以AC 为直径的圆与AC 边的高1BB 及其延长线交于P 、Q ,求证:M 、N 、P 、Q 四点共圆NCQPMC1B1BA例3 在等腰ABC ∆中,P 为底边BC 上任意一点,过点P 作两腰的平行线分别与AB 、AC 交于点Q 、R ,又点1P 是点P 关于QR 的对称点,求证:点1P 在ABC ∆的外接圆上例4 A 、B 、C 三点共线,O 点在直线外,1O 、2O 、3O 分别为OAB ∆、OBC ∆、OCA ∆的外心,求证:O 、1O 、2O 、3O 四点共圆例 5 在梯形A B C D 中,AB ‖DC ,DC AB >,K 、M 分别在AD 、BC 上,C B K DA M ∠=∠,求证:CKB DMA ∠=∠oBCAC M K DABCQP P1ARCB例6 如图,ABC ∆中,高BE 、CF 交于H ,且︒=∠135BHC ,G 为ABC ∆内的一点, 且GC GB =,A BGC ∠=∠3,连结HG ,求证:HG 平分BHF ∠例7 如图,ABC ∆内接于圆O ,AD 、BD 是圆O 的切线,作DE ∥BC 交AC 于E ,连结EO 并延长交BC 于F ,求证:FC BF =例8 正方形ABCD 的中心为O ,面积为21989cm ,P 为正方形内一点,︒=∠45OPB , 14:5:=PB PA ,求PBCBOPDAB 例9 如图,在平行四边形ABCD 中,BC AM ⊥于M ,CD AN ⊥于N ,若13=AB ,5=BM ,9=MC ,求MN 的长度例10 如图,已知直线AB 、AC 切圆O 于点B 、C , P 圆O 上一点,P 到AB 、AC 的距离分别为4厘米和6厘米,求P 到BC 的距离例11 在ABC ∆的边AB 、AC 上分别取点Q 、P ,使得A QCB PBC ∠=∠=∠21, 求证:CP BQ =CBQPAA例12在梯形A B C D 中,AD ‖BC ,1==BD BC ,AC AB =,1<CD ,︒=∠+∠180BDC BAC ,求CD 的长例13 在锐角ABC ∆中,AC AB ≠,H 是高AD 上一点,连结BH 并延长交AC 于点E ,连结CH 并延长交AB 于点F ,已知B 、C 、E 、F 四点共圆,求证:H 为ABC ∆的垂心例14 如图,P 圆O 外一点,PA 切圆O 于A ,PBC 是割线,PO AD ⊥于D ,求证:CDPCPB =CB D A BCBD例15 如图,已知,在凸五边形ABCDE 中,α3=∠B A E ,DE CD BC ==,且α2180-︒=∠=∠C DE B C D ,,求证:DAE CAD BAC ∠=∠=∠例16 如图,AD 为ABC ∆的一条高,l 是过D 的一条直线,E 、F 都是l 上的点,满足BE AE ⊥,CF AF ⊥,设M 、N 分别为BC 、EF 的中点,证明:MN AN ⊥例17 设有边长为1的正方形,试找出这个正方形的内接正三角形中面积最大的和面积最小的,并求出这两个面积例18 证明(托勒密定理)凸四边形A B C D 的四个顶点共圆的充要条件是BD AC BC AD CD AB ∙=∙+∙例19 一个凸六边形的顶点共圆,它的五条边长都为81,第六条边长为31,记第六条边为AB ,求A 引出的三条对角线的长度之和例20 证明(西姆松定理)从ABC ∆外一点D ,引三边BC 、AB 、AC 所在直线的垂线,垂足是L 、M 、N ,则点D 在ABC ∆的外接圆上的充要条件(点D 在ACB ∠内时)是L 、M 、N 共线,亦即MN LM LN +=。
中考数学圆中的重要模型四点共圆模型
圆中的重要模型-四点共圆模型四点共圆是初中数学的常考知识点,近年来,特别是四点共圆判定的题目出现频率较高。
相对四点共圆性质的应用,四点共圆的判定往往难度较大,往往是填空题或选择题的压轴题,而计算题或选择中四点共圆模型的应用(特别是最值问题),通常能简化运算或证明的步骤,使问题变得简单。
本文主要介绍四点共圆的四种重要模型。
四点共圆:若在同一平面内,有四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。
模型1、定点定长共圆模型(圆的定义)【模型解读】若四个点到一定点的距离相等,则这四个点共圆。
这也是圆的基本定义,到定点的距离等于定长点的集合。
条件:如图,平面内有五个点O、A、B、C、D,使得OA=OB=OC=OD,结论:A、B、C、D四点共圆(其中圆心为O)。
例1、(2023•连云港期中)如图,点O为线段BC的中点,点A、C、D到点O的距离相等,若∠ABC=40°,则∠ADC的度数是.例2.(2022秋·江西赣州·九年级校联考期中)如图,点O为线段AB的中点,点B,C,D到点O的距离相等,连接AC,BD.则下面结论不一定成立的是()A.∠ACB=90°B.∠BDC=∠BAC C.AC平分∠BAD D.∠BCD+∠BAD=180°例3.(2021·湖北随州·统考中考真题)如图,在R t A B C中,90∠A C B∠=︒,O为A B的中点,O D平分A O COF例4.(2022·北京·清华附中九年级阶段练习)如图,四边形A B C D 中,D A D B D C==,72BD C ∠=︒,则B A C∠的度数为______.模型2、定边对双直角共圆模型同侧型 异侧型 1)定边对双直角模型(同侧型)条件:若平面上A 、B 、C 、D 四个点满足90A B DA C D ∠=∠=︒,结论:A 、B 、C 、D 四点共圆,其中AD 为直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学满分之路(二) ——四点共圆一、使用定义解题圆的定义 平面上到一个定点的距离等于定长的点的集合叫做圆. 在题目中出现共端点的等线段时,可尝试作出圆辅助求解.例 (1)如图,四边形ABCD 中,DC ∥AB ,BC =1,AB =AC =AD =2,则BD 的长为______.(2)如图,在等腰△ABC中,AB AC =D 为BC 边上异于中点的点,点C 关于直线AD 的对称点为点E ,EB 的延长线与AD 的延长线交于点F ,则AD AF ⋅的值为______.E1. 如图,抛物线2y ax bx c =++经过点(2,5)A -,与x 轴相交于(1,0)B -,(3,0)C 两点. (1)求抛物线的函数表达式;(2)点D 在抛物线的对称轴上,且位于x 轴的上方,将△BCD 沿直线BD 翻折得到△'BC D ,若点'C 恰好落在抛物线的对称轴上,求点'C 和点D 的坐标;(3)设点P 是抛物线上位于对称轴右侧的一点,点Q 在抛物线的对称轴上,当△CPQ 为等边三角形时,求直线BP 的函数表达式.2. 问题背景如图1,等腰△ABC 中,AB =AC ,∠BAC =120°,作AD ⊥BC 于点D ,则D 为BC 的中点,∠BAD =12∠BAC =60°,于是2BC BDAB AB= 迁移应用(1)如图2,△ABC 和△ADE 都是等腰三角形,∠BAC =∠DAE =120°,D ,E ,C 三点在同一条直线上,连接BD .ⅰ)求证:△ADB ≌△AEC ;ⅱ)请直接写出线段AD ,BD ,CD 之间的等量关系式. 拓展延伸(2)如图3,在菱形ABCD 中,∠ABC =120°,在∠ABC 内作射线BM ,作点C 关于BM 的对称点E ,连接AE 并延长交BM 于点F ,连接CE ,CF .ⅰ)求证:△CEF 是等边三角形; ⅱ)若AE =5,CE =2,求BF 的长.图1图2图33. 如图,AB 是半圆⊙O 的直径,点C 为半圆⊙O 上的点,连接AC ,BC ,点E 是AC 的中点,点F 是射线OE 上一点.(1)如图1,连接F A ,FC ,若2AFC BAC ∠=∠,求证:F A ⊥AB ;(2)如图2,过点C 作CD ⊥AB 于点D ,点G 是线段CD 上一点(不与点C 重合),连接F A ,FG ,FG 与AC 相交于点P ,且AF FG =.①试猜想∠AFG 和∠B 的数量关系,并证明;②连接OG ,若OE BD =,90GOE ∠=,⊙O 的半径为2,求EP 的长.图1 图2二、圆内接四边形的性质与判定定理性质定理1 圆的内接四边形的对角互补.定理2 圆内接四边形的外角等于它的内角的对角.圆周角定理的推论同弧所对的圆周角相等.判定圆内接四边形判定定理1 如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.推论如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.圆内接四边形判定定理2 如果一个四边形一边与一对角线的夹角等于其对边与另一对角线的夹角,那么这个四边形的四个顶点共圆.上述定理在应用时的书写格式如下①∵A,B,C,D四点共圆,∴∠BAD+∠BCD=180°.②∵A,B,C,D四点共圆,∴∠DCE=∠BAD.③∵A,B,C,D四点共圆,∴∠ACB=∠ADB. ④∵∠BAD+∠BCD=180°,∴A,B,C,D四点共圆.⑤∵∠DCE=∠BAD,∴A,B,C,D四点共圆.⑥∵∠ACB=∠ADB,∴A,B,C,D四点共圆.EE4. 如图,矩形ABCD 的对角线AC ,BD 相交于点O ,过点O 作OE AC ⊥交AB 于点E ,若4BC =,△AOE 的面积为6,则sin BOE ∠的值为______.5. 如图,点B 在线段AC 上,点D ,E 在AC 同侧,90A C ∠=∠=,BD BE ⊥,AD BC =. (1)求证:AC AD CE =+;(2)若3AD =,5CE =,点P 为线段AB 上的动点,连接DP ,作PQ DP ⊥,交直线BE 与点Q ;ii )当点P 从A 点运动到AC 的中点时,求线段DQ 的中点所经过的路径(线段)长.DBP6. 如图,已知△ABC 是等边三角形,点D ,E 分别在边AC ,AB 上,且CD AE =,BD 与CE 相交于点P . (1)求证:△ACE ≌△CBD ;(2)如图2,将△CPD 沿直线CP 翻折得到对应的△CPM ,过C 作CG ∥AB ,交射线PM 于点G ,PG 与BC 相交于点F ,连接BG .ⅰ)试判断四边形ABGC 的形状,并说明理由;ⅱ)若四边形ABGC的面积为,1PF =,求CE 的长.图1图2三、与圆有关的比例线段相交弦定理 圆内的两条弦,被交点分成的两条线段长的积相等.割线定理 从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等. 切割线定理 从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段的比例中项.上述定理在应用时的书写格式如下 由相交弦定理, 得PA PB PC PD ⋅=⋅.由割线定理, 得PA PB PC PD ⋅=⋅.由切割线定理, 得2PA PB PC =⋅.7. 如图,已知AB 是⊙O 的直径,C 为⊙O 上一点,延长BC 至D ,使CD =BC ,CE ⊥AD 于E ,BE 交⊙O 于F ,AF 交CE 于P . 求证:PE =PC .P8. 如图1,线段AB 是⊙O 的直径,弦CD ⊥AB 于点H ,点M 是CBD 上任意一点,AH =4,CD =16.(1)求⊙O 的半径r 的长度;10r =; (2)求tan ∠CMD ;(3)如图2,直线BM 交直线CD 于点E ,直线MH 交⊙O 于点N ,连接BN 交CE 于点F ,求H E H F ⋅的值.图1图29. 已知BC 为⊙O 的直径,AC 为⊙O 的切线,C 为切点,AD =BD .(1)如图1,求证:∠A =45°;(2)如图2,E 为⊙O 上一点,连接DE 交BC 于点F ,过点F 作BC 的垂线交BE 于点G ,求证:FG =FC ;(3)如图3,在(2)的条件下,若EG BDF 的面积为15(BF >BD ),求⊙O 的面积.图1BC图2CB图3BC10. (蝴蝶定理)如图,过⊙O的弦PQ的中点M引任意两条弦AB,CD,连接AD,BC分别交PQ于X,Y两点. 求证:MX=MY.证明:分别取AD ,CB 的中点E ,F , 连接OE ,OF ,OM ,OX ,OY ,ME ,MF , ∵∠A =∠C ,∠D =∠B ,∴△ADM ∽△CBM , ∴AM ADCM CB=,又AD =2AE ,CB =2CF , ∴22AD AE AE CB CF CF ==,∴AM AECM CF=,又∠A =∠C , ∴△AEM ∽△CFM ,∴∠AEM =∠CFM ,∵点M ,E ,F 分别是⊙O 的弦PQ ,AD ,CB 的中点, ∴OM ⊥PQ ,OE ⊥AD ,OF ⊥CB ,∴∠OEX +∠OMX =180°,∠OFY +∠OMY =180°, ∴O ,M ,X ,E 四点共圆,O ,M ,Y ,F 四点共圆, ∴∠MOX =∠AEM ,∠MOY =∠CFM ,又∠AEM =∠CFM , ∴∠MOX =∠MOY ,又OM =OM ,∠OMX =∠OMY =90°, ∴△OMX ≌△OMY ,∴MX =MY . 证法二证明:过点D 作DE ∥PQ 交⊙O 于另一点E ,连接MO 并延长交DE 于E , ①当PQ 为直径时,四边形ACBD 为矩形,易证MX =MY ; ②当PQ 不是直径时,由垂径定理推论,得OM ⊥PQ ,又DE ∥PQ , ∴MN ⊥DE ,又MN 过圆心O ,∴MN 垂直平分DE , ∴MD =ME ,∴∠MDE =∠MED ,又PQ ∥DE ,∴∠PMD =∠MDE ,∠QME =∠MED , ∴∠PMD =∠QME ,∠QME =∠MDE ,∵C ,D ,B ,E 四点共圆,∴∠MDE +∠CBE =180°, ∴∠QME +∠CBE =180°, ∴M ,E ,B ,Y 四点共圆,∴∠MEY =∠MBC ,又∠MBC =∠ADC ,∴∠ADC =∠MEY ,又MD =ME ,∠PMD =∠QME , ∴△MDX ≌△MEY ,∴MX =MY .证明:过X 作'XX AB ⊥于'X ,过X 作"XX CD ⊥于"X , 过Y 作'YY CD ⊥于'Y ,过Y 作"YY AB ⊥于"Y ,∵∠A =∠C ,∠D =∠B ,''90AX X CY Y ∠=∠=,""90CX X BY Y ∠=∠=, ∴△'AX X ∽△'CY Y ,△"DX X ∽△"BY Y , ∴''AX XX CY YY =,……①,""DX XX BY YY =,……②, ①×②,得'"'"AX DX XX XX CY BY YY YY ⋅=⋅, ∴'""'AX DX XX XX CY BY YY YY ⋅=⋅⋅,又由相交弦定理及平行线分线段成比例定理,得PX QX MX MXQY PY MY MY ⋅=⋅⋅, ∴22()()()()MP MX MP MX MX MP MY MP MY MY -⋅+=-⋅+,即222222MP MX MX MP MY MY -=-, 根据比例的基本性质,得22222222222222()1()MP MX MX MP MX MX MP MP MY MY MP MY MY MP --+====--+, ∴22MX MY =,∴MX =MY . 证法四证明:连接PA ,PD ,QC ,QB ,根据共圆定理,(共圆定理:同圆或等圆中的三角形面积比等于三边乘积之比) 得PAD QCB S PA PD AD PA PD ADS QB QC BC QB QC BC∆∆⋅⋅==⋅⋅⋅⋅, 又△PAM ∽△BQM ,△PDM ∽△CQM ,△ADM ∽△CBM , ∴22PAD AMDQCB CMBS PA PD AD AM MP AM AM S S QB QC BC MQ MC MC MC S ∆∆∆∆=⋅⋅=⋅⋅==, ∴QCB PAD AMD CMB S S S S ∆∆∆∆=,即PX QYMX MY=, ∴1MY QY MY QY MQ MX PX MX PX MP +====+, ∴MX =MY .B证明:连接AO 并延长交⊙O 于另一点E ,连接CO 并延长交⊙O 于另一点F ,连接BF ,DE 交于点G , 六边形CFBAED 内接于⊙O ,CF 交AE 于点O ,FB 交ED 于点G ,BA 交DC 于点M ,根据帕斯卡定理,得M ,O ,G 三点共线, 连接MG ,GX ,GY ,∵AE ,CF 为⊙O 的直径,∴∠ADE =90°,∠CBF =90°, ∵MP =MQ ,PQ 不是⊙O 的直径,(PQ 为直径时,易证) ∴OM ⊥PQ ,∴D ,G ,M ,X 四点共圆,B ,G ,M ,Y 四点共圆, ∴∠MGX =∠ADM ,∠MGY =∠CBM ,又∠ADM =∠CBM , ∴∠MGX =∠MGY ,又MG =MG ,∠GMX =∠GMY , ∴△GMX ≌△GMY , ∴MX =MY .帕斯卡定理 如果一个六边形内接于一条二次曲线(圆、椭圆、双曲线、抛物线),那么它的三对对边的交点在同一条直线上.B中考不考系列(二)——2019IMO第2题在三角形ABC中,点A1在边BC上,点B1在边AC上. 点P和Q分别在线段AA1和BB1上,且满足PQ平行于AB. 在直线PB1上取点P1,使得点B1严格位于点P与点P1之间,并且∠PP1C=∠BAC. 类似地,在直线QA1上取点Q1,使得点A1严格位于点Q与点Q1之间,并且∠CQ1Q=∠CBA.证明:点P,Q,P1,Q1共圆.证明:延长1AA ,1BB 分别交△ABC 的外接圆于2A ,2B ,连接22A B , ∵PQ ∥AB ,∴22ABB PQB ∠=∠,又222ABB AA B ∠=∠, ∴222PQB AA B ∠=∠,∴22,,,P Q A B 四点共圆,连接2B C ,∵1PPC BAC ∠=∠,2BB C BAC ∠=∠, ∴12PPC BB C ∠=∠,∴121,,,P B B C 四点共圆,连接12PB ,∵11212B PB B CB ∠=∠,222AA B ACB ∠=∠, ∴2122B PP B A P ∠=∠,∴122,,,P A P B 四点共圆,连接2A C ,∵1CQ Q CBA ∠=∠,2CA A CBA ∠=∠, ∴12CQ Q CA A ∠=∠,∴121,,,Q A A C 四点共圆,连接12Q A ,∵11212AQ A ACA ∠=∠,222BB A BCA ∠=∠, ∴2122A QQ A B Q ∠=∠,∴122,,,Q B Q A 四点共圆, ∴2112,,,,,P Q A Q P B 六点共圆, ∴点11,,,P Q P Q 共圆.上述答案是从官方答案翻译而来.【附】官方答案.。
