传热学课件第九章1
合集下载
传热学第九章

角系数的完整性
9-1 辐射传热的角系数
(3)角系数的可加性
从表面1上发出而落到表面2上的总能量,等于落到表面2上 各部分的辐射能之和,于是有
注意,利用角系数可加性时,只有对角系数符号中第二个角码 是可加的,对角系数符号中的第一个角码则不存在类似的关系。
9-1 辐射传热的角系数 3. 角系数的计算方法
试计算: (1)板1的自身辐射; (2)板1的有效辐射; (3)板1的投入辐射; (4)板1的反射辐射; (5)板1,2的净辐射换热量。
§ 9-4 气体辐射的特点及其计算
辐射性气体: 具有发射和吸收辐射能的能力的气体。
工业上常见的温度范围内 常见的辐射性气体: 二氧化碳、水蒸气、二氧化硫、甲烷、氟里昂等三原子、多原子及 结构不对称的双原子气体(一氧化碳)
ቤተ መጻሕፍቲ ባይዱ
9.3.2 多表面封闭系统网络法求解的实施步骤
9.3.2 多表面封闭系统网络法求解的实施步骤
3. 求解代数方程组,计算各表面的有效辐射。
例如
已知三个表面温度T1, T2, T3;以及 A1, A2, A3, ε1, ε2, ε3, X1,2, X1,3, X2,3。
确定每个表面的有效辐射J1, J2, J3和 净辐射热量Φ1, Φ2, Φ3。
81
9.6 综合传热问题
82
9.6 综合传热问题
83
9.6 综合传热问题 解:
求解的结果为,
这样的测量误差在工业上是可以接受的。
84
85
9.6 综合传热问题 辐射传热系数
86
第9章 测试题
• 试述气体辐射的基本特点,气体能当做灰体来处 理吗?请说明原因。(2003年,华电,15分)
• 两块平行放置且相互靠得很近的灰体平壁,它们 的黑度均为0.8,壁1和2的温度分别为400和30℃ ,试计算壁2的(1)辐射换热量;(2)本身辐 射;(3)有效辐射。( 2003年,华电,15分)
9-1 辐射传热的角系数
(3)角系数的可加性
从表面1上发出而落到表面2上的总能量,等于落到表面2上 各部分的辐射能之和,于是有
注意,利用角系数可加性时,只有对角系数符号中第二个角码 是可加的,对角系数符号中的第一个角码则不存在类似的关系。
9-1 辐射传热的角系数 3. 角系数的计算方法
试计算: (1)板1的自身辐射; (2)板1的有效辐射; (3)板1的投入辐射; (4)板1的反射辐射; (5)板1,2的净辐射换热量。
§ 9-4 气体辐射的特点及其计算
辐射性气体: 具有发射和吸收辐射能的能力的气体。
工业上常见的温度范围内 常见的辐射性气体: 二氧化碳、水蒸气、二氧化硫、甲烷、氟里昂等三原子、多原子及 结构不对称的双原子气体(一氧化碳)
ቤተ መጻሕፍቲ ባይዱ
9.3.2 多表面封闭系统网络法求解的实施步骤
9.3.2 多表面封闭系统网络法求解的实施步骤
3. 求解代数方程组,计算各表面的有效辐射。
例如
已知三个表面温度T1, T2, T3;以及 A1, A2, A3, ε1, ε2, ε3, X1,2, X1,3, X2,3。
确定每个表面的有效辐射J1, J2, J3和 净辐射热量Φ1, Φ2, Φ3。
81
9.6 综合传热问题
82
9.6 综合传热问题
83
9.6 综合传热问题 解:
求解的结果为,
这样的测量误差在工业上是可以接受的。
84
85
9.6 综合传热问题 辐射传热系数
86
第9章 测试题
• 试述气体辐射的基本特点,气体能当做灰体来处 理吗?请说明原因。(2003年,华电,15分)
• 两块平行放置且相互靠得很近的灰体平壁,它们 的黑度均为0.8,壁1和2的温度分别为400和30℃ ,试计算壁2的(1)辐射换热量;(2)本身辐 射;(3)有效辐射。( 2003年,华电,15分)
传热学-第九章 辐射计算

X1, 2
1,2 1,2 A 1,2 B
X1, 2i
i 1
n
A1 Eb1 X 1,2 A1 Eb1 X 1,2 A A1 Eb1 X 1,2 B X 1,2 X 1,2 A X 1,2 B
再来看一下2 对 1 的能量守恒情况: 2 ,1 2 A ,1 2 B ,1
X 1,2 X 2,1
1 A1 1 A2
A1
A2
X d 1, d 2 dA1 X d 2, d 1dA2
A
A1 1
1
cos 1 cos 2 dA1dA2
A2
A1
1 A2
A2
A1
r cos 1 cos 2 dA1dA2
2
(9-4a)
A2
r
2
(9-4b)
的电流、电位差和电阻比拟热辐射中的热流、热势差与热
阻,用电路来比拟辐射热流的传递路径。但需要注意的是, 该方法也离不开角系数的计算,所以,必须满足漫灰面、 物性均匀以及投入辐射均匀的条件。
热势差与热阻
上节公式(9-12):
J Eb ( 1)q
1
改写为:
Eb J q 1
1, 2 A1 Eb1 X 1, 2 A2 Eb 2 X 2,1 A1 X 1, 2 ( Eb1 Eb 2 ) 的热辐射 到达表面 2的部分 的热辐射 到达表面 1的部分
图9-13 黑体系统的 辐射换热
表面1发出 表面 2发出
例题9-4 一直径d=0.75m的圆筒形埋地式加热炉采用电加热。 在操作过程中需要将炉子顶盖移去一段时间,设此时筒身温 度为 500K ,筒底为 650K 。环境温度为 300K 。试计算顶盖移 去期间单位时间内的热损失。设筒身及底面均可作为黑体。
传热学 第九章 辐射换热的计算

灰体——多次反射、吸收
9-2 两表面之间的辐射换热过程
1. 黑体表面之间的辐射换热
任意位置的两个黑体表面1、2,从表面1发出并直接投射
到表面2上的辐射能为
1 2 A1 X 1,2 E b1
从表面2发出并直接投射到表面1上的辐射能为
21 A2 X 2 ,1 E b 2
两个表面之间的直接辐射换热量为
X 1,2 X 2 ,1 1
A2 a
A1
9-1 角系数
4. 角系数的计算方法
(2) 代数法
由三个垂直于纸面方向无限长的非凹表面构成的封闭空腔,
三个表面的面积分别为A1、A2、A3 。
X i ,i 0
根据角系数的完整性
角系数的相对性
A1 X 1, 2 A1 X 1, 3 A1
A1 X 1,2 A2 X 2 ,1
Eb1 cos 1 cos 2 dA1dA2
1d 1
dd11
2
2 Lb1 dA1 cos
2
r
Eb1
dA2 cos 2
Lb1
d1
r2
9-1 角系数
2. 角系数的定义式
12
cos 1 cos 2
cos 1 cos 2
dA1dA2
E b1
dA1dA2 E b1
2
2
A1 A2
A1 A2
r
r
表面1对表面2的角系数为
X 1,2
12
A1 Eb1
1
A1
cos 1 cos 2
A1 A2 r 2 dA1dA2
1
A2
cos 1 cos 2
9-2 两表面之间的辐射换热过程
1. 黑体表面之间的辐射换热
任意位置的两个黑体表面1、2,从表面1发出并直接投射
到表面2上的辐射能为
1 2 A1 X 1,2 E b1
从表面2发出并直接投射到表面1上的辐射能为
21 A2 X 2 ,1 E b 2
两个表面之间的直接辐射换热量为
X 1,2 X 2 ,1 1
A2 a
A1
9-1 角系数
4. 角系数的计算方法
(2) 代数法
由三个垂直于纸面方向无限长的非凹表面构成的封闭空腔,
三个表面的面积分别为A1、A2、A3 。
X i ,i 0
根据角系数的完整性
角系数的相对性
A1 X 1, 2 A1 X 1, 3 A1
A1 X 1,2 A2 X 2 ,1
Eb1 cos 1 cos 2 dA1dA2
1d 1
dd11
2
2 Lb1 dA1 cos
2
r
Eb1
dA2 cos 2
Lb1
d1
r2
9-1 角系数
2. 角系数的定义式
12
cos 1 cos 2
cos 1 cos 2
dA1dA2
E b1
dA1dA2 E b1
2
2
A1 A2
A1 A2
r
r
表面1对表面2的角系数为
X 1,2
12
A1 Eb1
1
A1
cos 1 cos 2
A1 A2 r 2 dA1dA2
1
A2
cos 1 cos 2
精品工程类本科大三课件《传热学》传热-第9章-1

X 2,3
A2
A3 2 A2
A1
l2
l3 l1 2l2
A2 X 2,1 A2 X 2,3 A2
X1,3
A1 A3 2 A1
A2
l1 l3 l2 2l1
A3 X 3,1 A3 X 3,2 A3
X1,2
A1 A2 2 A1
A3
l1 l2 l3 2l1
X1,2 1 X1,ac X1,bd
A2 X 2,1 A2 X 2,3 A2 A3 X 3,1 A3 X 3,2 A3
A1 X1,2 A2 X 2,1 A1 X1,3 A3 X 3,1 A2 X 2,3 A3 X 3,2
A1 X1,2
A1 X1,3
A2 X 2,3
1 2
( A1
A2
A3 )
A1 X1,2 A1 X1,3 A1
(2)角系数的完整性:
对于N个表面包围并形成一个封 闭腔,那么根据角系数的定义,
n
X1,1 X1,2 X1,3 L X1,n X1,i 1 i 1 (3)角系数的可加性(分解性): A1Eb1 X1,2 A1Eb1 X1,2a A1Eb1 X1,2b X1,2 X1,2a X1,2b A2 Eb2 X 2,1 A2a Eb2 X 2a,1 A2b Eb2 X 2b,1 A2 X 2,1 A2a X 2a,1 A2b X 2b,1
第8章小结
重点掌握以下内容:
(1)有关热辐射的基本概念:吸收比、反射比、 透射比、黑体、灰体、漫射体、人工黑体、辐射强度 、辐射力、发射率(黑度)、立体角、温室效应、选 择性表面等;
(2)热辐射的基本定律:普朗克定律、斯忒藩— 玻耳兹曼定律、维恩位移定律、兰贝特定律、基尔 霍夫定律。
传热学第九章优秀课件

在前面假设的基础上,并已知冷热流体的进出口温度,现 在来看图9-13中微元换热面dA一段的传热。温差为:
t th tc d t d th d tc
在固体微元面dA内,两种流体的换热量为:
1 ho d o 2
Φ l(t fi t fo ) (do2 )
d
ddo2
l(t fi (d
t o2 )
fo )
2
1
22d
o
2
1 h2do22d Leabharlann ddo2do222
h2
dcr
or
Bi do2h2 2
2
可见,确实是有一个极值存在,那么,到底是极大值,还是 极小值呢?从热量的基本传递规律可知,应该是极大值。也 就是说,do2在do1 ~ dcr之间,是增加的,当do2大于dcr时, 降低。
(4) 板式换热器:由一组几何结构相同的平行薄平板叠加所 组成,冷热流体间隔地在每个通道中流动,其特点是拆卸清 洗方便,故适用于含有易结垢物的流体。
(5) 螺旋板式换热器:换热表面由两块金属板卷制而成, 有点:换热效果好;缺点:密封比较困难。
4 简单顺流及逆流换热器的对数平均温差 传热方程的一般形式:
ho oAo(two tfo )
肋面总效率
o
(A1
f
Ao
A2)
hi1Ai tf1A i tf2 ho1oAo h 1iA i(tf 1 htofA 2oi)Ao
定义肋化系数:Ao Ai
则传热系数为
k
1
1
1
hi hoo
所以,只要o 1就可以起到强化换热的效果。
4 带保温层的圆管传热——临界热绝缘直径
(3) 交叉流换热器:间壁式换热器的又一种主要形式。其 主要特点是冷热流体呈交叉状流动。交叉流换热器又分管 束式、管翅式和板翅式三种。
传热学-第九章

1 G1
1 E1
1Eb1
J1
1 G1
G1
表面间的辐射换热作准备。如图所示,对
表面1来讲,净辐射换热量q为
q J1 G1 E1 1G1 1Eb1 1G1
消去上式中的G1,并考虑到1=1,可得
J1 Eb1 (
1
1
1) q
即:
J Eb (
1
两圆盘间距相对半径足够小,即L<<R ,则L→0,Xd1,2=1
问:如果大圆盘是一个圆环,怎么求?
2. 角系数的性质
根据角系数的定义及解析式,可导出角系数的性质。
(1) 相对性 由前面的式(a)和(b)可以看出
X d 1,d 2
I b1 cos1dA1d dA2 cos1 cos2 Eb1dA1 r2
第九章 辐射传热的计算
本章重点
(1) 掌握角系数的定义、性质及其计算方法 (2) 理解效辐射和投入辐射的概念 (3) 理解表面热阻及空间热阻的概念 (4) 掌握两个表面及三个表面热辐射系统的网络计算方法 (5) 掌握辐射换热的强化与削弱的方法 (6) 了解气体辐射的基本特点
§9-1 辐射传热的角系数
1
1Eb1
J1
1 G1
G1
1 G1
数X1,2是:表面1直接投射到表面2上的能量,占表面1辐射能量 的百分比。即
X 1, 2
角系数的应用条件
表面1对表面2的投入辐射 表面1的有效辐射
(1) 所研究的表面是漫射面 (2) 在不同地点上向外发射的辐射热流密度均匀
纯几何
因 子
(2) 微元面对微元面的角系数
dA1 cos 1 cos 2
X d 2, d 1
1 E1
1Eb1
J1
1 G1
G1
表面间的辐射换热作准备。如图所示,对
表面1来讲,净辐射换热量q为
q J1 G1 E1 1G1 1Eb1 1G1
消去上式中的G1,并考虑到1=1,可得
J1 Eb1 (
1
1
1) q
即:
J Eb (
1
两圆盘间距相对半径足够小,即L<<R ,则L→0,Xd1,2=1
问:如果大圆盘是一个圆环,怎么求?
2. 角系数的性质
根据角系数的定义及解析式,可导出角系数的性质。
(1) 相对性 由前面的式(a)和(b)可以看出
X d 1,d 2
I b1 cos1dA1d dA2 cos1 cos2 Eb1dA1 r2
第九章 辐射传热的计算
本章重点
(1) 掌握角系数的定义、性质及其计算方法 (2) 理解效辐射和投入辐射的概念 (3) 理解表面热阻及空间热阻的概念 (4) 掌握两个表面及三个表面热辐射系统的网络计算方法 (5) 掌握辐射换热的强化与削弱的方法 (6) 了解气体辐射的基本特点
§9-1 辐射传热的角系数
1
1Eb1
J1
1 G1
G1
1 G1
数X1,2是:表面1直接投射到表面2上的能量,占表面1辐射能量 的百分比。即
X 1, 2
角系数的应用条件
表面1对表面2的投入辐射 表面1的有效辐射
(1) 所研究的表面是漫射面 (2) 在不同地点上向外发射的辐射热流密度均匀
纯几何
因 子
(2) 微元面对微元面的角系数
dA1 cos 1 cos 2
X d 2, d 1
传热学 第九章 答案

X 1, 2 + X 1, 3 = 1 X 2 ,1 + X 2 , 3 = 1 X 3 ,1 + X 3 , 2 = 1
求解得, 求解得,
A1 X 1, 2 = A2 X 2 ,1 A1 X 1, 3 = A3 X 3 ,1 A2 X 2 , 3 = A3 X 3 , 2
X 1, 2 =
A1 + A2 − A3 2 A1
Φ 1, 2 = 0
E b1 = E b 2
第9章 辐射传热的计算
A1 X 1, 2 = A2 X 2 ,1
§9.1 辐射传热的角系数 辐射传热的角系数
二、角系数的性质
2.完整 2.完整性 完整性
有n个表面组成的封闭系统, 个表面组成的封闭系统,据能量守恒可得: 据能量守恒可得:
X i ,1 + X i ,2 + X i ,3 + ⋯ + X i , n = ∑ X i , j = 1
X 2,1 =
第9章 辐射传热的计算
§9.1 辐射传热的角系数 辐射传热的角系数
三、角系数的计算
2.代数分析法 2.代数分析法
利用角系数的性质, 利用角系数的性质,通过求解代数方程获得角系数。 通过求解代数方程获得角系数。 图(a)、(b):
X 1,1 = 0
A1 X 2,1 = A2
X 1,2 = 1
第9章 辐射传热的计算
§9.1 辐.角系数概念引出的原因 1.角系数概念引出的原因
辐射换热的计算除了与辐射换热表面的辐射和吸收特性有关 外,还与辐射换热表面的相对位置有关。 还与辐射换热表面的相对位置有关。
2.角系数概念引出的假定 2.角系数概念引出的假定
X 1,2
传热学第九章
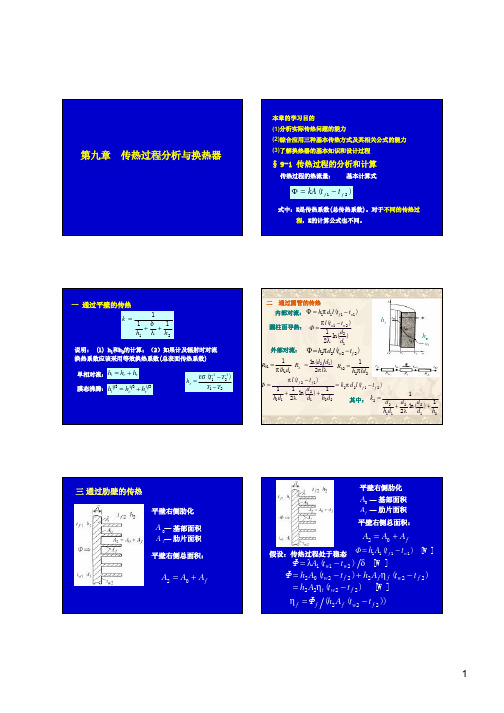
Φ=
tf1 −tf 2 1 δ 1 + + h1 A1 λA1 h2ηt βA1
Φ = h2 A2ηt (t w 2 − t f 2 ) [W]
ηt = A0 + A f η f A2 = A0 + A f η f A0 + A f
热阻图:
若以肋壁面积A2为基础,传热系数为:
= k1 A1 t f 1 − t f 2 1 k1 = 1 δ 1 + + h1 λ h2ηt β
TB,out TA,in (tube side)
增加管程
T B , in (shell side) T A , in (tube side) T A , out T B , out
TB ,in (shell side)
TA,out
TB ,out
进一 步增加管程和壳程
TA,in (tube side)
d[ ∆ t ( x )] = − µ k ∆ t ( x ) dA
代入上式得
[LMTD ]∆tm =
由于式中出现了对数,故常把∆tm称为对数平均温差。
顺流:
∆tm =
∆t′ − ∆t′′ ∆t′ ln ∆t ′′
2. 顺流换热器的平均温差
逆流时: 逆流换热器中冷 、热流体温度的沿 程变
化如下图。如果 µ取如下 形式,则上述 推导过程完全适合于逆流换热器:
l 管程(Tube Pass):由管子组成的通道 l 壳程(Shell Pass):管外壳内通道 l 管程数:流体在管内流动方向数 l 壳程数:流体在壳内流动方向数 l 壳管式换热器的命名 壳程数-管程数 1-2型:壳程为1,管称为2;2-4型:壳程为2,管称为4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黑体系统的辐射换热
表面1发出 表面 2发出
黑体辐射系统传热量的计算关键是求得角系数。
8.2.2 有效辐射
投入辐射:单位时间内投射到单位面积上的总辐射能,记为G。 1、有效辐射:单位时间内离开单位面积 的总辐射能为该表面的有效辐射,记为J
自身射辐射E
有效辐射
投入辐射 G 被反射辐射的部分 G
有效辐射示意图
解:
A2 R2 X 1, X 2, X 1, 1 2 1 2 2 A1 2 R 1 X 1, 2 2
A2 1 1 X 2 X 2, X 1, 1 2 解: 1, A1 4 2 1 X 1, 2 8
解:
X1, 0.5 2
【例】试确定如图所示的表面1对表面2的角系数X1,2 。
(2)任意两个非凹表面间的角系数 如图所示表面和假定在垂直于纸面的方向上表面的长 度是无限延伸的,只有封闭系统才能应用角系数的完整性, 为此作辅助线ac和bd,与ab、cd一起构成封闭腔。
A1 两个非凹表面及假想面组 成的封闭系统
根据角系数的完整性:
X ab,cd 1 X ab,ac X ab,bd
cos 1 cos 2 dA2 X d 1, 2 A2 r2
dA1
上式积分可得
A1 X 1, 2 cos 1 cos 2 dA2 dA1 2 A1 A2 r
dω 1
dA2
即
X 1, 2
1 A1
cos 1 cos 2 dA2 dA1 A1 A2 r 2
上两式联立消去G1,得到J与表面净辐射换热量之间的关系:
J q G1 q
E 1 1 q Eb ( 1)q
注:式中的各个量均是对同一表面而言的,且以向外界的净放热量为正值。
8.2.3 两漫灰表面组成的封闭腔的辐射换热
两个物体组成的辐射换热系统
两个等温漫灰表面封闭系统内,两个表面的净换热量为
注:利用这样的分析方法,扩大线图的使用,可以得出很多几何结构简单的角系数
8.2 两封闭系统的辐射换热
8.2.1 封闭腔以及两黑体表面组成的封闭腔间
1、封闭腔模型
2、两黑表面封闭系统的辐射换热
1,2 A1 Eb1 X 1,2 A2 Eb 2 X 2,1 A1 X 1,2 ( Eb1 Eb 2 ) 的热辐射 到达表面 2的部分 的热辐射 到达表面 1的部分
上述方法又被称为交叉线法。注意:这里所 谓的交叉线和不交叉线都是指虚拟面断面的线, 或者说是辅助线。
【例】求下列图形中的角系数
解:
A1 X 1, A2 X 2, 2 1
A2 X 1, X 2, 2 1 A1
X1, 2
X 2, 1 1
X 1,2 4 1 3 3 2 R 4 2R
X 1, 2 X 1, 2 a X 1, 2 b
如把表面2进一步分成若干小块,则有
X 1, 2 X 1, 2 i
i 1 n
注意,利用角系数可加性时,只有对角系数符号中第二个 角码是可加的,对角系数符号中的第一个角码则不存在类 似的关系。
从表面2上发出而落到表面1上的辐射能,等于 从表面2的各部分发出而落到表面1上的辐射能之和, 于是有
1,2 A1 J1 X 1,2 A2 J 2 X 2,1
因为
E 1 1 J q Eb ( 1)q
1 1 J 2 A2 A2 Eb 2 ( 1) 2,1 2
1,2 [ A1 Eb1 ( 1
J1 A1 A1 Eb1 (
1
1)1,2
dA1
工程上已经将大量几何结构角系数的求解结果绘制成图线。 教材中给出了一些二维结构角系数的计算公式以及三种典 型三维几何结构的计算式和工程计算图线。
2、代数分析法
利用角系数的方法称为代数分析法。 (1)三个非凹表面组成的封闭系统
图8-5 三个非凹表面组成的封闭系统
由角系数完整性
X 1, 2 X 1, 3 1 X 2 ,1 X 2 , 3 1 X 3 ,1 X 3 , 2 1
由角系数相对性
A3 A1 A2
A1 X 1, 2 A2 X 2 ,1 A1 X 1, 3 A3 X 3 ,1 A2 X 2 , 3 A3 X 3 , 2
8.1.3 角系数的计算方法
直接积分法 求解角系数的方法 代数分析法 几何分析法
1、直接积分法
• 按角系数的基本定义通过求解多重积分而获得 角系数的方法 • 如图所示的两个有限大小的面积,可以得到
X d 1,d 2 cos 1 cos 2 dA2 r2
dω 1
dA2
微元面积dA1对 A2 的角系数为
表面的反射比,可表示成
1 1
考察表面温度均匀、表面辐射特性为常数的表面1。根 据有效辐射的定义,表面1的有效辐射有如下表达式:
J1 E1 1G1 1Eb1 (1 1 )G1
在表面外能感受到的表面辐射 就是有效辐射,它也是用辐射探测 仪能测量到的单位表面积上的辐射 2 功率 W / m。
ab ac bc X ab,ac 2ab
X ab,bd
ab bd ad 2ab
两个非凹表面及假想面组 成的封闭系统
X ab,cd
(bc ad ) (ac bd ) 2ab
交叉线之和 不交叉线之和 2 表面A1的断面长度
两个非凹表面及假想面组 成的封闭系统
1
1)1,2 ] X 1,2 [ A2 Eb 2 (
1
2
1) 2,1 ] X 2,1
根据能量守恒有
1,2 2,1
1,2 [ A1 Eb1 (
1
1
1)1,2 ] X 1,2 [ A2 Eb 2 (
1
2
1)1,2 ] X 2,1
1, 2
X
i 1
n
1, i
1
注:若表面1为非凹表面时,X1,1 = 0;
角系数的完整性
若表面1为凹表面, 1, 0 X 1
3、角系数的可加性
从表面1上发出而落到表面2上的总能量,等于落到表面2上 各部分的辐射能之和,于是有
A1 E b1 X 1, 2 A1 E b1 X 1, 2a A1 E b1 X 1, 2b
三表面封闭空间 角系数的确定
上述方程解得: X 1, 2
X 1, 3
A1 A2 A3 2 A1
A1 A3 A2 2 A3 A2 A3 A1 2 A2
X 2,3
由于垂直纸面方向的长度相同,则有:
X 1,2 X 1,3 X 2,3 l1 l2 l3 2l1 l1 l3 l2 2l1 l2 l3 l1 2l2
2
dAc dA2 cos 2 d 2 r r2
dA2 cos 1 cos 2 X dA1 ,dA2 r 2
1
两微元面间的辐射
dA2 cos 1 cos 2 X dA1 ,dA2 r 2
同理:
整理得:
dA1 cos 1 cos 2 X dA2 ,dA1 r2
1 1 1 A1
Eb1 Eb 2 1 2 1 A X 1, 2 2 A2 1
J1
J2
Eb1
1 1 1 A1
Eb 2
1 A1 X 1,2
1 2 2 A2
两封闭表面间的辐射换热网络图
1, 2
1 1 1 A1
Eb1 Eb 2 1 2 1 A X 1, 2 2 A2 1
解:表面2对表面A和表面2对表面1+A的角系
数都可以从图9-8中查出:
Y
2
X2,A=0.10;X2,1+A=0.15。
由角系数的可分性X2,1+A=X2,1+X2,A可得:
X2,1=X2,1+A-X2,A。
Z
1
再根据角系数的互换性A1X1,2 =A2X2,1 即可得: X1,2=A2X2,1/A1=A2(X2,1+A-X2,A)/A1=2.5(0.15-0.10)/1=0.125
传热学
建筑环境与热能工程系
热动教研室
第八章 辐射换热的计算
8.1
辐射换热的角系数
两个表面之间的辐射换热量与两个表面之间的相对位置 有很大关系
表面相对位置的影响
a图中两表面无限接近,相互间的换热量最大; b图中两表面位于同一平面上,相互间的辐射换热量为零。
由图可以看出,两个表面间的相对位置不同时,一个表面 发出而落到另一个表面上的辐射能的百分数随之而异,从 而影响到换热量。
A1 X 1, 2 A2 X 2,1
2、角系数的完整性
对于由几个表面组成的封闭系统,据能量守衡原理,从任何 一个表面发射出的辐射能必全部落到封闭系统的个表面上。 因此,任何一个表面对封闭腔各表面的角系数之间存在下列 关系:
X 1 ,1 X 1 , 2 X 1 , 3 X 1 , n 1
8.1.2.
角系数的性质
1、角系数的相对性
一个微元表面到另一个微元表面的角系数
由dA1发出的落到dA2上的辐射能 I b1 d A1 cos 1 d X dA1 ,dA2 由dA1发出的辐射能 Eb1 d A1
E b1 I b1 Eb1 : 辐射力 I b1:定向辐射强度
A2 Eb 2 X 2,1 A2 a Eb 2 X 2 a ,1 A2b Eb 2 X 2b,1
A2 X 2,1 A2a X 2a ,1 A2b X 2b,1
X 2 , 1 X 2 a ,1
A2a A X 2 b ,1 2 b A2 A2
表面1发出 表面 2发出
黑体辐射系统传热量的计算关键是求得角系数。
8.2.2 有效辐射
投入辐射:单位时间内投射到单位面积上的总辐射能,记为G。 1、有效辐射:单位时间内离开单位面积 的总辐射能为该表面的有效辐射,记为J
自身射辐射E
有效辐射
投入辐射 G 被反射辐射的部分 G
有效辐射示意图
解:
A2 R2 X 1, X 2, X 1, 1 2 1 2 2 A1 2 R 1 X 1, 2 2
A2 1 1 X 2 X 2, X 1, 1 2 解: 1, A1 4 2 1 X 1, 2 8
解:
X1, 0.5 2
【例】试确定如图所示的表面1对表面2的角系数X1,2 。
(2)任意两个非凹表面间的角系数 如图所示表面和假定在垂直于纸面的方向上表面的长 度是无限延伸的,只有封闭系统才能应用角系数的完整性, 为此作辅助线ac和bd,与ab、cd一起构成封闭腔。
A1 两个非凹表面及假想面组 成的封闭系统
根据角系数的完整性:
X ab,cd 1 X ab,ac X ab,bd
cos 1 cos 2 dA2 X d 1, 2 A2 r2
dA1
上式积分可得
A1 X 1, 2 cos 1 cos 2 dA2 dA1 2 A1 A2 r
dω 1
dA2
即
X 1, 2
1 A1
cos 1 cos 2 dA2 dA1 A1 A2 r 2
上两式联立消去G1,得到J与表面净辐射换热量之间的关系:
J q G1 q
E 1 1 q Eb ( 1)q
注:式中的各个量均是对同一表面而言的,且以向外界的净放热量为正值。
8.2.3 两漫灰表面组成的封闭腔的辐射换热
两个物体组成的辐射换热系统
两个等温漫灰表面封闭系统内,两个表面的净换热量为
注:利用这样的分析方法,扩大线图的使用,可以得出很多几何结构简单的角系数
8.2 两封闭系统的辐射换热
8.2.1 封闭腔以及两黑体表面组成的封闭腔间
1、封闭腔模型
2、两黑表面封闭系统的辐射换热
1,2 A1 Eb1 X 1,2 A2 Eb 2 X 2,1 A1 X 1,2 ( Eb1 Eb 2 ) 的热辐射 到达表面 2的部分 的热辐射 到达表面 1的部分
上述方法又被称为交叉线法。注意:这里所 谓的交叉线和不交叉线都是指虚拟面断面的线, 或者说是辅助线。
【例】求下列图形中的角系数
解:
A1 X 1, A2 X 2, 2 1
A2 X 1, X 2, 2 1 A1
X1, 2
X 2, 1 1
X 1,2 4 1 3 3 2 R 4 2R
X 1, 2 X 1, 2 a X 1, 2 b
如把表面2进一步分成若干小块,则有
X 1, 2 X 1, 2 i
i 1 n
注意,利用角系数可加性时,只有对角系数符号中第二个 角码是可加的,对角系数符号中的第一个角码则不存在类 似的关系。
从表面2上发出而落到表面1上的辐射能,等于 从表面2的各部分发出而落到表面1上的辐射能之和, 于是有
1,2 A1 J1 X 1,2 A2 J 2 X 2,1
因为
E 1 1 J q Eb ( 1)q
1 1 J 2 A2 A2 Eb 2 ( 1) 2,1 2
1,2 [ A1 Eb1 ( 1
J1 A1 A1 Eb1 (
1
1)1,2
dA1
工程上已经将大量几何结构角系数的求解结果绘制成图线。 教材中给出了一些二维结构角系数的计算公式以及三种典 型三维几何结构的计算式和工程计算图线。
2、代数分析法
利用角系数的方法称为代数分析法。 (1)三个非凹表面组成的封闭系统
图8-5 三个非凹表面组成的封闭系统
由角系数完整性
X 1, 2 X 1, 3 1 X 2 ,1 X 2 , 3 1 X 3 ,1 X 3 , 2 1
由角系数相对性
A3 A1 A2
A1 X 1, 2 A2 X 2 ,1 A1 X 1, 3 A3 X 3 ,1 A2 X 2 , 3 A3 X 3 , 2
8.1.3 角系数的计算方法
直接积分法 求解角系数的方法 代数分析法 几何分析法
1、直接积分法
• 按角系数的基本定义通过求解多重积分而获得 角系数的方法 • 如图所示的两个有限大小的面积,可以得到
X d 1,d 2 cos 1 cos 2 dA2 r2
dω 1
dA2
微元面积dA1对 A2 的角系数为
表面的反射比,可表示成
1 1
考察表面温度均匀、表面辐射特性为常数的表面1。根 据有效辐射的定义,表面1的有效辐射有如下表达式:
J1 E1 1G1 1Eb1 (1 1 )G1
在表面外能感受到的表面辐射 就是有效辐射,它也是用辐射探测 仪能测量到的单位表面积上的辐射 2 功率 W / m。
ab ac bc X ab,ac 2ab
X ab,bd
ab bd ad 2ab
两个非凹表面及假想面组 成的封闭系统
X ab,cd
(bc ad ) (ac bd ) 2ab
交叉线之和 不交叉线之和 2 表面A1的断面长度
两个非凹表面及假想面组 成的封闭系统
1
1)1,2 ] X 1,2 [ A2 Eb 2 (
1
2
1) 2,1 ] X 2,1
根据能量守恒有
1,2 2,1
1,2 [ A1 Eb1 (
1
1
1)1,2 ] X 1,2 [ A2 Eb 2 (
1
2
1)1,2 ] X 2,1
1, 2
X
i 1
n
1, i
1
注:若表面1为非凹表面时,X1,1 = 0;
角系数的完整性
若表面1为凹表面, 1, 0 X 1
3、角系数的可加性
从表面1上发出而落到表面2上的总能量,等于落到表面2上 各部分的辐射能之和,于是有
A1 E b1 X 1, 2 A1 E b1 X 1, 2a A1 E b1 X 1, 2b
三表面封闭空间 角系数的确定
上述方程解得: X 1, 2
X 1, 3
A1 A2 A3 2 A1
A1 A3 A2 2 A3 A2 A3 A1 2 A2
X 2,3
由于垂直纸面方向的长度相同,则有:
X 1,2 X 1,3 X 2,3 l1 l2 l3 2l1 l1 l3 l2 2l1 l2 l3 l1 2l2
2
dAc dA2 cos 2 d 2 r r2
dA2 cos 1 cos 2 X dA1 ,dA2 r 2
1
两微元面间的辐射
dA2 cos 1 cos 2 X dA1 ,dA2 r 2
同理:
整理得:
dA1 cos 1 cos 2 X dA2 ,dA1 r2
1 1 1 A1
Eb1 Eb 2 1 2 1 A X 1, 2 2 A2 1
J1
J2
Eb1
1 1 1 A1
Eb 2
1 A1 X 1,2
1 2 2 A2
两封闭表面间的辐射换热网络图
1, 2
1 1 1 A1
Eb1 Eb 2 1 2 1 A X 1, 2 2 A2 1
解:表面2对表面A和表面2对表面1+A的角系
数都可以从图9-8中查出:
Y
2
X2,A=0.10;X2,1+A=0.15。
由角系数的可分性X2,1+A=X2,1+X2,A可得:
X2,1=X2,1+A-X2,A。
Z
1
再根据角系数的互换性A1X1,2 =A2X2,1 即可得: X1,2=A2X2,1/A1=A2(X2,1+A-X2,A)/A1=2.5(0.15-0.10)/1=0.125
传热学
建筑环境与热能工程系
热动教研室
第八章 辐射换热的计算
8.1
辐射换热的角系数
两个表面之间的辐射换热量与两个表面之间的相对位置 有很大关系
表面相对位置的影响
a图中两表面无限接近,相互间的换热量最大; b图中两表面位于同一平面上,相互间的辐射换热量为零。
由图可以看出,两个表面间的相对位置不同时,一个表面 发出而落到另一个表面上的辐射能的百分数随之而异,从 而影响到换热量。
A1 X 1, 2 A2 X 2,1
2、角系数的完整性
对于由几个表面组成的封闭系统,据能量守衡原理,从任何 一个表面发射出的辐射能必全部落到封闭系统的个表面上。 因此,任何一个表面对封闭腔各表面的角系数之间存在下列 关系:
X 1 ,1 X 1 , 2 X 1 , 3 X 1 , n 1
8.1.2.
角系数的性质
1、角系数的相对性
一个微元表面到另一个微元表面的角系数
由dA1发出的落到dA2上的辐射能 I b1 d A1 cos 1 d X dA1 ,dA2 由dA1发出的辐射能 Eb1 d A1
E b1 I b1 Eb1 : 辐射力 I b1:定向辐射强度
A2 Eb 2 X 2,1 A2 a Eb 2 X 2 a ,1 A2b Eb 2 X 2b,1
A2 X 2,1 A2a X 2a ,1 A2b X 2b,1
X 2 , 1 X 2 a ,1
A2a A X 2 b ,1 2 b A2 A2
