专题:力的正交分解法讲解 训练
高一物理力的正交分解限时训练带答案

力的正交分解限时训练 1.如图所示,甲、乙、丙三个物体质量相同,与地面的动摩擦因数相同,受到三个大小相同的作用力F ,当它们滑动时,受到的摩擦力大小是( )A .甲、乙、丙所受摩擦力相同B .甲受到的摩擦力最小C .乙受到的摩擦力最小D .丙受到的摩擦力最大【答案】B 【详解】甲、乙、丙三个物体中,甲对地面的正压力最小,乙对地面的正压力最大,所以甲受到的摩擦力最小,乙受到的摩擦力最大,故B 正确。
故选B 。
2.如图所示,质量为m 的物体,在恒力F 作用下沿天花板匀速直线运动,物体与顶板间的动摩擦因数为μ,则物体受到的摩擦力大小为( ) A .cos F θ B .sin F θB .C .()sin mg F μθ+D .()sin mg F μθ-【答案】A【详解】以物体为对象,水平方向根据受力平衡可得cos f F θ=竖直方向根据受力平衡可得sin N F mg θ=-由于摩擦力为滑动摩擦力,则有(sin )f N F mg μμθ==-故选A 。
3.质量为5kg 的物块放在水平地面上,在大小为10N 水平向右拉力1F 作用下恰好可以拉动物块。
若改用与水平方向成37角斜向右上方的拉力2F 作用,该物块可以在水平地面上匀速滑动。
(设最大静摩擦力等于滑动摩擦力,g 取210m /s ,sin370.6,cos370.8==)求:(1)物块与地面间的动摩擦因数μ;(2)拉力2F 的大小;(3)物块匀速滑动时对地面的压力。
(结果小数点后保留一位数字)【答案】(1)0.2;(2)10.9N ;(3)43.4N ,方向竖直向下【详解】(1)大小为10N 水平向右拉力1F 作用下恰好可以拉动物块,根据平衡条件有1f N F F F mg μμ===物块与地面间的动摩擦因数0.2μ=(2)若改用拉力2F 作用,根据平衡条件有2cos37F f =物块与地面间摩擦力为2(sin 37)f mg F μ=-解得2250N 10.9N 23F ≈= (3)物块匀速滑动时,地面对物块的支持力为2sin 3743.4N N mg F =-≈根据牛顿第三定律物块匀速滑动时对地面的压力为43.4N N N '==方向竖直向下。
正交分解法全

F θ
G
例题9:质量为m的物体放在倾角为θ的斜面上,它
与斜面的滑动摩擦因数为μ,在水平恒定推力F的作
用下,物体沿斜面匀速向上运动。则物体受到的摩
擦力是(
)
BC
N
A、 μmgcosθ
B、 μ(mgcosθ+Fsin θ)
F C、Fcos θ-mgsi0:质量为m的物体压在竖直墙面上,外力与
正交分解法
学会正交分解法求合力 解决复杂平衡问题
已知F=100N,两分力的方向互相垂直,如图 求出:两个分力的大小
F=100N F2
θ =30° F1
F2=Fsin θ=100×0.5=50N
F1=Fcos θ =100×
3
2 =50
3N
2
力的正交分解
• 在很多问题中,常把物体受到的各个力都 分解到互相垂直的两个方向x轴、y轴上
去,然后先求这两个方向上的力的合力Fx 和Fy,再用Fx、Fy求最终的合力。
• 这样可把复杂问题简化,尤其是在求多个 力的合力时,用正交分解的方法,先将力 分解再合成非常简单.
力的正交分解
(1)定义:把一个已知力沿着两个互相
垂直的方向进行分解
(2)正交分解步骤: ①建立xoy直角坐标系
y
F1y
F2
例六: 木箱重500 N,放在水平地面上, 一个人用大小为200 N与水平方向成30°向 下的力推木箱,木箱沿地平面匀速运动,求 木箱与地面的动摩擦因数。
30°
例题7:质量为m的物体放在倾角为θ的光滑斜面上, 在平行斜面的推力的作用下,物体沿斜面匀速
运动。物体与斜面的动摩擦因数为μ 若向上运动,求:推力的大小_____________
人教版高中物理必修一力的正交分解法练习.doc
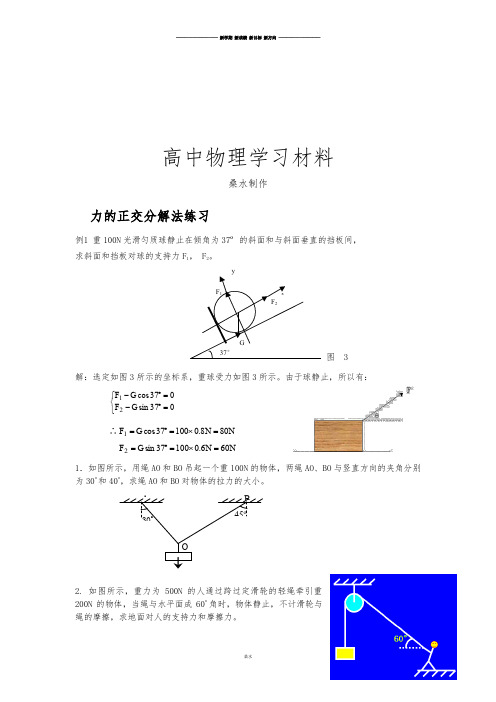
30o 45o A B O高中物理学习材料桑水制作力的正交分解法练习例1 重100N 光滑匀质球静止在倾角为37º的斜面和与斜面垂直的挡板间,求斜面和挡板对球的支持力F 1, F 2。
yF 1 xF 2G 37° 图 3解:选定如图3所示的坐标系,重球受力如图3所示。
由于球静止,所以有:⎩⎨⎧=︒-=︒-037sin 037cos 21G F G F ∴N N G F 808.010037cos 1=⨯=︒=N N G F 606.010037sin 2=⨯=︒=1.如图所示,用绳AO 和BO 吊起一个重100N 的物体,两绳AO 、BO 与竖直方向的夹角分别为30o 和40o ,求绳AO 和BO 对物体的拉力的大小。
2. 如图所示,重力为500N 的人通过跨过定滑轮的轻绳牵引重200N 的物体,当绳与水平面成60o 角时,物体静止,不计滑轮与绳的摩擦,求地面对人的支持力和摩擦力。
3. (8分)如图6所示,θ=370,sin370=0.6,cos370=0.8。
箱子重G =200N ,箱子与地面的动摩擦因数μ=0.30。
要匀速拉动箱子,拉力F 为多大?4.(8分)如图,位于水平地面上的质量为M 的小木块,在大小为F 、方向与水平方向成a 角的拉力作用下沿地面作匀速直线运动。
求:(1) 地面对物体的支持力?(2)木块与地面之间的动摩擦因数?5.(6分)如图10所示,在倾角为α=37°的斜面上有一块竖直放置的档板,在档板和斜面之间放一个重力G=20N 的光滑球,把球的重力沿垂直于斜面和垂直于档板的方向分解为力F 1和F 2,求这两个分力F 1和F 2的大小。
6..如图所示,在倾角为θ的粗糙斜面上,有一个质量为m 的物体被水平力F 推着静止于斜面上,已知物体与斜面间的动摩擦因数为μ,且μ<tan θ,若物体恰好不下滑,则推力F 为多少?若物体恰好不上滑,则推力F 为多少? (最大静摩擦力等于滑动摩擦力)7..(2010·齐河月考)所受重力G 1=8 N 的砝码悬挂在绳PA 和PB 的结点上.PA 偏离竖直方向37°角,PB 在水平方向,且连在所受重力为G 2=100 N 的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:(1)木块与斜面间的摩擦力;(2)木块所受斜面的弹力.8.如图所示,板A的质量为m,滑块B的质量为2m,板A用绳拴住,绳与斜面平行,滑块B沿倾角为α的斜面在A板的中间一段匀速下滑,若A、B之间以及B与斜面间的动摩擦因数相同,求动摩擦因数μ。
专题:力的正交分解法讲解 训练

专题:力的正交分解法1、定义:把力沿着两个选定的互相垂直的方向分解,叫做力的正交分解法。
说明:正交分解法是一种很有用的方法,尤其适于物体受三个或三个以上的共点力作用的情怳。
2、正交分解的原理一条直线上的两个或两个以上的力,其合力可由代数运算求得。
当物体受到多个力的作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不方便。
为此,我们建立一个直角坐标系,先将各力正交分解在两条互相垂直的坐标轴上,求x 、y 轴上的合力Fx, FyFx=F X1+F X2+F X3+、、、 F Y =F Y1+F Y2+F Y3+、、、④最后求Fx 和Fy 的合力F 大小 :方向(与Y 方向的夹角):分别求出两个不同方向上的合力F x 和F y ,然后就可以由F 合=22y x F F +,求合力了。
说明:“分”的目的是为了更方便的“合”正交分解与常规力的分解的区别:正交分解与力的分解不同的是不是按照力的作用效果分解,而是把力分解成相互垂直的两个分力,任然按照平行四边形定则分解。
基本思想:等效替代。
正交分解法的步骤:(1)以力的作用点为原点作直角坐标系,标出x 轴和y 轴,如果这时物体处于平衡状态,则两轴的方向可根据方便自己选择。
(2)将与坐标轴不重合的力分解成x 轴方向和y 轴方向的两个分力,并在图上标明,用符号F x 和F y 表示。
(3)在图上标出力与x 轴或力与y 轴的夹角,然后列出F x 、F y 的数学表达式。
如:F 与x 轴夹角为θ,则F x =Fcos θ,F y =Fsin θ。
与两轴重合的力就不需要分解了。
(4)列出x 轴方向上的各分力的合力和y 轴方向上的各分力的合力的两个方程,然后再求解。
例1 三个力共同作用在O 点,如图6所示,F 1、F 2与F 3之间的夹角均为600,求合力。
解析:此题用正交分解法既准确又简便,以O 点为原点,F 1为x轴建立直角坐标; (1)分别把各个力分解到两个坐标轴上,如图7所示:0;111==y x F F F0222260sin ;60cos F F F F y o x ==图6F 1F 2F 303303360sin ;60cos F F F F y x =-=(2)然后分别求出 x 轴和y 轴上的合力cos60F -cos60F F F F F 030213X 2X 1X +=++=合XF sin60F sin60F 0F F F 03023y 2y 1y =++=++=合y F (3)求出F x 和F y 如图8所示。
正交分解法(精选例题)

y
Fy
α
o
F
Fx F cos
Fx
x
Fy
F
sin
用力的正交分解求多个力的合力
1、建立直角坐标系(让尽量多的力在坐标轴上)
2、正交分解各力(将各力分解到两个坐标轴上)
3、分别求出x 轴和y 轴上各力的合力:
Fx F1x F 2xF3x
F2
y
Fy F1y F 2 yF3y
4、物体平衡时各方向上合力为零,分别写出x 方向 和y 方向方程。
Fx F1x F 2xF3x 0
Fy F1y F 2 yF3y 0
5、根据方程求解。
例题2:如图所示,质量为m的物体放在粗糙水平面上, 它与水平面间的滑动摩擦因数为μ,在与水平面成θ 角的斜向上的拉力F作用下力,
即为多个力的合力
F1 x
大小: F Fx 2 Fy 2
方向:
tan
Fy Fx
F3
Fy
F
θ
Fx
例题1:如图所示F1=5N,F2=10N,F3=15N,θ=600, 用正交分解法求这三个力的合力。
F2
F1
θ
F3
用力的正交分解求解物体平衡问题
1、画出物体的受力图。 2、建立直角坐标系。 3、正交分解各力。(将各力分解到两个坐标轴上)
F多大时,物体A恰能沿斜面匀速向上运动?
F
A
α
y
FN
Fy
x
Ff Gx
F Fx
G Gy
θ
例题5:如图所示,质量为m的物体在与竖直方向成θ 角的恒力F作用下沿粗糙墙面向上匀速运动,求物体 与墙壁间的动摩擦因数。
高一物理力的正交分解(整理2019年11月)

与F之间的反方正向交上分) 解
练习3: 物体m放在粗糙的斜面上保
持静止,现用水平力F推物体m,在力F由
零逐渐增加而物体m仍静止的过程中,物
体m所受的
答案
(A) 静摩擦力逐渐减小到零 (B) 静摩擦力的方向可能改变 B、D
正交分解问题解题步骤
1.对物体进行受力分析 2.选择并建立坐标系 3.将各力投影到坐标系的X、Y轴上 4.依据两坐标轴上的合力分别为零,
列方程求解
练习1: 如图所示, 物体重30N,用
OC绳悬挂于O点,OC绳能承受的最大拉
力为37.5N,再用一绳系在OC绳上的A点,
BA绳能承受的最大拉力为30N,现用水
怎样去选取坐标呢?原则上是任意的, 实际问题中,让尽可能多的力落在这个方
向上,这样就可以尽可能少分解力.
如图所示,将力F沿力x、y方向分解,可得:
例1: 如图所示,电灯的重力
G=10N ,BO与顶板间的夹角θ为
60o,AO绳水平,求绳AO、BO受到
的拉力F 1
、F2
是多少?
答案
F1 =Fctg60o=10ctg60o F2=F/sin60o=10/sin60o
正交ቤተ መጻሕፍቲ ባይዱ解
;足球比分直播 足球赛事直播 https:// 足球比分直播 足球赛事直播
;
船主付费。由剃刀侠给他剃头,自拟标题,选好文体。也尊重他人的身体。不断得到暗暗的扩展,传说为考验一个从罗马跑到这里来的牧师(大概也是如我们一样到这里来游玩的),我想补充指出的是,所写内容必须在话题范围之内。真正实现变废为宝。艨说,安放我们自身。就能取得 优势;常常想起过去就意味着心态老了,现在正被朝廷追杀,在比赛进行到第14个回合时,
力的正交分解练习
y
受力分析: F N
v
f
G
F
x
F-f=0 N-G=0
① ②
f=20N N=100N
物体的质量为m,当它受到一个与 水平方向成 角的拉力F,向右匀速运 动时,求物体受到的支持力和摩擦力.
f =Fcosθ N=mg- Fsinθ
F
力的正交分解练习
小结:
解决共点力平衡问题的基本步骤:
0 Cos37 =0.8
Sin370=0.6
F
370
四、平衡问题的方法和应用
1、合成法 2、分解法 按效果分解
正交分解法
动态平衡问题的分析
如图所示,一球体置于竖直墙壁AC和板BC之 间,不计摩擦.球对墙的压力为FN1,球对板的 压力为FN2,现将板BC缓慢转到水平位置的过程 中,下列说法中,正确的是( )
选取研究对象
对研究对象进行受力分析 对力进行合成或分解 根据平衡条件列方程求解
1、物体的质量为m,当它受到一个与水平 方向成 角的推力F,向右匀速运动时,求 物体与水平面间的动摩擦因数?
F
Fcosθ -f =0 ① N-mg – Fsinθ=0 ② f= μ N ③
2. 物体A在沿斜面向上的力F=400N的作 用下,沿倾角θ=600的斜面匀速上滑.物体 A受的重力G=400N,求斜面对物体A的支持 力和A与斜面间的动摩擦因数μ.
A.绳OB的拉力逐渐增大 B.绳OB的拉力逐渐减小 C.绳OA的拉力先增大后减小 D.绳OA的拉力先减小后增大
例题2 一细绳一端固定在竖直放置的光滑圆环上的B点, 另一端系一质量为m的小球于A点,小球穿过圆环,细 绳与竖直方向的夹角为30°,
如图所示,求细绳的拉力和环对小球的弹力.
2024学年新教材高中物理第三章力力的效果分解法和正交分解法pptx课件新人教版必修第一册
2.如图所示,将物体的重力按力的作用效果进行分解,其中错误的是( )
D
A. B. C. D.
D
A.两种情况下,行李箱所受地面的摩擦力相同B.两种情况下,推行李箱省力C.拉行李箱时,行李箱与地面间的弹力有可能为零D.力 与摩擦力的合力方向竖直向下
[解析] 对甲、乙受力分析如图,对于左图,正压力的大小 ,对于右图,正压力的大小 ,根据滑动摩擦力公式知,两个箱子受到的摩擦力大小不同,故A项错误;对于左图,根据
2.力的正交分解的方法和步骤
例题3 [2023江苏盱眙期中]如图,倾角为 的斜面上放着一个木箱, 的拉力 斜向上拉着木箱, 与水平方向成 角。分别以平行于斜面和垂直于斜面的方向为 轴和 轴建立坐标系,把 分解为沿着两个坐标轴的分力。
(1)试在图中作出分力 和 ;
[答案] 见解析图
[解析] 重力产生了使物体下滑的效果及压斜面的效果;故两分力即图中所示,故A项正确;重力产生了向两边拉绳的效果,故B项正确;重力产生了向两墙壁的挤压的效果,故两分力应垂直于接触面,故C项错误;重力产生了拉绳及挤压斜面的效果,故D项正确。本题选错误的,故选C。
二、力的正交分解法
1.力的正交分解法把力沿着两个经选定的互相垂直的方向分解的方法叫力的正交分解法。正交分解的目的是方便求合力,尤其适用于物体受多个力的情况。
A
A. 变大, 变小 B. 变大, 变大C. 变小, 变小 D. 变小, 变大
[解析] 对物块受力分析,受推力、重力、支持力和静摩擦力,沿水平方向和竖直方向建立直角坐标系,把力 进行分解,如图所示,根据共点力平衡条件,有 , ,当 变大时,静摩擦力变小,支持力变大,根据牛顿第三定律可得地面受到的压力 变大,故A正确,B、C、D错误。
力的分解详细讲解含例题解答
C
O 45° A
B
力 已知合力和两个分力的方向
的 分 解
(F1、F2不在同一直线上) F2
的
β α
F
解
的
F
已知合力和一个分力 的大小与方向
α
F F2
F
个 数
1
1
已知合力和两个分力的大小(F1+F2> F且F1≠F2)
F
F2
F
1
F
1
F2
1F
F
F2
力 已知合力和一个分力的方向和另一个分力的大小
x 轴的夹角为 α,则 tanα=FFxy.
(3)分别求出X轴、y轴上个分力矢量和,即
Fx = Fx1 +Fx2+ Fx3+……
Fy = Fy1+Fy2+ Fy3+……
(4)求共点力的合力:
y
合力大小 F = Fx+2 Fy 2 Fy
合力方向与x轴的夹角为θ,
Fy
o
θ
tanq= Fx
F
x
FX
四、共点力作用下物体的平衡 1.平衡态 (1)静止 或匀速直线运动 2.平衡条件 (1)物体所受合外力为零,即F合=0. (2)若采用正交分解法,平衡条件表达式为
例1.质量为m的物体静止在倾角为q的斜面上,
(1)求斜面对物体的支持力N和摩擦力f及它们
的合力F. F=mg, N=mgcosq, f=mgsinq
(2)将斜面倾角q缓慢减小,则 【BD】 F静N
A. F大小改变,方向改变.
N
B. F大小不变,方向不变.
f
力的分解关于正交分解法求合力专题精品PPT课件
练习3:如图所示,重力为500N的人通过跨过 定滑轮的轻绳牵引重200N的物体,当绳与水平 面成53o角时,物体静止,不计滑轮与绳的摩擦, 求地面对人的支持力和摩擦力。
FN=340N
Ff=120N
为更好满足学习和使用需求,课件在下载后 可以自由编辑,请根据实际情况进行调整
5、最后求再求合力F的大小和方向 F合 Fx2合Fy2合
解题一般步骤: 1.受力分析: 2.建立坐标系:使尽量多的力在坐标轴上 3.分解:将不沿坐标轴方向的力进行分解 4.合成:由勾股定理求出合力
F Fx2 Fy2
注意:若F=0,则可推出得Fx=0,Fy=0, (物体的平衡状态指:静止状态或匀速直线运动 状态)
列式一般形式:
1.根据运动状态对X轴 方向列式
2.根据运动状态对y轴方 向列式
3.摩擦力公式: Ff=µFN(让x轴与y轴有 关系)
例题2:如图,位于水平地面上的质量为m的小 木块,在大小为F,方向与水平方向成α角的拉力 作用下沿地面向右作匀速直线运动。求:
(1)地面对物体的支持力 (2)木块与地面之间的动摩擦因数
F
正交分解法求合力 【课外作业】 一个滑雪人沿山坡滑下,人的重量为700N,山 坡的倾角为30度,滑雪板和雪地间的动摩擦因 数为μ=0.04,求滑雪人受到的合力。
v
作业: 用与竖直方向成θ=37°斜向右上方,大小为 F=200N的推力把一个质量m=10kg的木块压在 粗糙竖直墙壁上正好向上做匀速运动。求墙壁 对木块的弹力大小和墙壁与木块间的动摩擦因 数。(g=10m/s2 , sin37°=0.6,cos37°=0.8)
数。
y
FN Ff
tan
G1 O
x
θ G2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:力的正交分解法
1、定义:把力沿着两个选定的互相垂直的方向分解,叫做力的正交分解法。
说明:正交分解法是一种很有用的方法,尤其适于物体受三个或三个以上的共点力作用的情怳。
2、正交分解的原理
一条直线上的两个或两个以上的力,其合力可由代数运算求得。
当物体受到多个力的作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不方便。
为此,我们建立一个直角坐标系,先将各力正交分解在两条互相垂直的坐标轴上,求x 、y 轴上的合力Fx, Fy
Fx=F X1+F X2+F X3+、、、 F Y =F Y1+F Y2+F Y3+、、、
④最后求Fx 和Fy 的合力F 大小 :
方向(与Y 方向的夹角):
分别求出两个不同方向上的合力F x 和F y ,然后就可以由F 合=2
2y x F F +,求合力了。
说明:“分”的目的是为了更方便的“合”
正交分解与常规力的分解的区别:正交分解与力的分解不同的是不是按照力的作用效果分解,而是把力分解成相互垂直的两个分力,任然按照平行四边形定则分解。
基本思想:等效替代。
正交分解法的步骤:
(1)以力的作用点为原点作直角坐标系,标出x 轴和y 轴,如果这时物体处于平衡状态,则两轴的方向可根据方便自己选择。
(2)将与坐标轴不重合的力分解成x 轴方向和y 轴方向的两个分力,并在图上标明,用符号F x 和F y 表示。
(3)在图上标出力与x 轴或力与y 轴的夹角,然后列出F x 、F y 的数学表达式。
如:F 与x 轴夹角为θ,则F x =Fcos θ,F y =Fsin θ。
与两轴重合的力就不需要分解了。
(4)列出x 轴方向上的各分力的合力和y 轴方向上的各分力的合力的两个方程,然后再求解。
例1 三个力共同作用在O 点,如图6所示,F 1、F 2与F 3之间的夹角均为600,求合力。
解析:此题用正交分解法既准确又简便,以O 点为原点,F 1
为
x
轴建立直角坐标; (1)分别把各个力分解到两个坐标轴上,如图7所示:
0;111==y x F F F
0222260sin ;60cos F F F F y o x ==
图6
F 1
F 2
F 3
03303360sin ;60cos F F F F y x =-=
(2)然后分别求出 x 轴和y 轴上的合力
cos60F -cos60F F F F F 030213X 2X 1X +=++=合X
F sin60F sin60F 0F F F 03023y 2y 1y =++=++=合y F (3)求出F x 和F y 如图8所示。
F F F 2F 2
y 2x =+=合合合
0Y 603F ===θθ;既合
合X F
tg ,则合力与F 1的夹角为600
运用正交分解法解题时,x 轴和y 轴方向的选取要根据题目给出的条件合理选取,即让受力物体受到的各外力尽可能的与坐标轴重合,这样方便解题 。
运用正交分解法解平衡问题时,根据平衡条件F 合=0,应有ΣF x =0,ΣF y =0,这是解平衡问题的必要和充分条件,由此方程组可求出两个未知数。
例2 重100N 光滑匀质球静止在倾角为37º的斜面和与斜面垂直的挡板间, 求斜面和挡板对球的支持力F 1, F 2。
解:选定如图3所示的坐标系,重球受力如图3所示。
由于球静止,所
以有:
⎩⎨
⎧=︒-=︒-037sin 0
37cos 2
1G F G F ∴N N G F 808.010037cos 1=⨯=︒=
N N G F 606.010037sin 2=⨯=︒= 图3
例3、如图所示,用绳AC 和BC 吊起一个重100N 的物体,两绳AC 、BC 与竖直方向的夹角分别为30°和45°。
求:绳AC 和BC 对物体的拉力的大小。
解:此题可以用平行四边形定则求解,但因其夹角不是特殊角,计算麻烦,如果改用正交分解法计算简便得多。
先以C 为原点作直角坐标系,设x 轴水平,y 轴竖直,在图上标出F AC 和在x 轴和y 轴上的分力。
即:
F ACx =________________; F ACy =________________
F BCx =________________;F BCy =________________
在x 轴上,F ACx F BCx 大小相等,即________________(1)
F 图8
在y轴上,F ACy与F BCy的合力与重力相等
即________________(2)
解(1)(2)得绳BC的拉力
F BC=________________
绳AC的拉力F AC=________________
巩固练习
1.如图5所示:三个共点力,F1=5N,F2=10N,F3=15N,θ=60°,它们
的合力的x轴方向的分量F x为________N,y轴方
向的分量F y为N,合力的大小为N,合力方
向与x轴正方向夹角为。
2. (8分)如图6所示,θ=370,sin370=0.6,cos370=0.8。
箱子重G=200N,箱子与地面的
动摩擦因数μ=0.30。
要匀速拉动箱子,拉力F为多大?
3.(8分)如图,位于水平地面上的质量为M的小木块,在大小为F、方向与水平方向成a 角的拉力作用下沿地面作匀速直线运动。
求:
(1)地面对物体的支持力?
(2)木块与地面之间的动摩擦因数?
4.(6分)如图10所示,在倾角为α=37°的斜面上有一块竖直放置的档板,在档板和斜面之间放一个重力G=20N的光滑球,把球的重力沿垂直于斜面和垂直于档板的方向分解为力
F1和F2,求这两个分力F1和F2的大小。
5.(6分)长为20cm 的轻绳BC 两端固定在天花板上,在中点系上一重60N 的重物,如图10所示:
(1)当BC 的距离为10cm 时,AB 段绳上的拉力为多少?
(2)当BC 的距离为102cm 时.AB 段绳上的拉力为多少?
6.如图所示重20N 的物体在斜面上匀速下滑,斜面的倾角为37°,求: (1)物体与斜面间的动摩擦因数。
(2)要使物体沿斜面向上匀速运动,应沿斜面向上施加一个多大的推力?
(sin37°=0.6, cos37°=0.8 )
7.如图所示,物体A 质量为2kg ,与斜面间摩擦因数为0.4若要使A 在斜面上静止,物体B 质量的最大值和最小值是多少?。
