八年级上册数学模型构建专题:共顶点的特殊等腰三角形
最新人教版初中八年级上册数学《共顶点的等腰三角形问题》精品教案

等腰三角形的两条腰相等,如果两个等腰三角形共顶点且顶角相等,那么 将两条腰分配到不同的两个三角形中会得到全等三角形,会发现某些线段在数 量和位置上有着特殊的关系.
常见的有共顶点的等腰直角三角形和等边三角形,我们一起来探究.
类型一:共顶点的等腰三角形问题
如图,AB=AC,AE=AF,∠BAC=∠EAF=90°,BE、CF交于M,求
证:⑴BE=CF;⑵BE⊥CF;
C
⑴证明:∵∠BAC=∠EAF=90°,
EM 1 A
B∴∠BAC+∠1=∠EAF+∠1 即∠EAB=∠FAC
又∵AB=AC,AE=AF
∴△EAB≌△FAC
F
∴BE=CF
类型一:共顶点的等腰三角形问题
如图,AB=AC,AE=AF,∠BAC=∠EAF=90°,BE、CF交于M,求
如果两个等腰三角形共顶点且顶角相等,那么将两条腰分配到不同的两个 三角形中会得到全等三角形,并且我们会发现:改变两个三角形的相对位置并 不会改变所得的三角形的全等关系.
课后小知识
学习方法指导
同学们,天道酬勤,一个人学习成绩的优劣取决于他的学习 能力,学习能力包括三个要素:
规范的学习行为; 良好的学习习惯; 有效的学习方法。 只要做好以上三点,相信你一定会成为学习的强者。 加油!加油!加油!
类型二:共顶点的等边三角形
如图所示,△ACM和△BCN都为等边三角形,连接AN、BM,求证:
AN=பைடு நூலகம்M.
N M
A
1
2 3
B
C
证明: ∵△ACM和△BCN都为等边三角形, ∴∠1=∠3=60° ∴∠1+∠2=∠3+ ∠2 即∠ACN=∠MCB ∵CA=CM,CB=CN ∴△CAN≌△CMB(SAS) ∴AN=BM
模型构建专题:“手拉手”模型——共顶点的等腰三角形压轴题三种模型全攻略(学生版)

模型构建专题:“手拉手”模型【考点导航】目录【典型例题】【类型一共顶点的等边三角形】【类型二共顶点的等腰直角三角形】【类型三共顶点的一般等腰三角形】【典型例题】【类型一共顶点的等边三角形】1(2023·全国·八年级假期作业)如图所示,△ABC和△ADE都是等边三角形,且点B、A、E在同一直线上,连接BD交AC于M,连接CE交AD于N,连接MN.(1)求证:BD=CE;(2)求证:△ABM≌△ACN;(3)求证:△AMN是等边三角形.【变式训练】1(2023春·山西运城·八年级统考期中)如图,点C为线段AB上一点,△DAC、△ECB都是等边三角形,AE、DC交于点M,DB、EC交于点N,DB、AE交于点P,连接MN,下列说法正确的个数有个.①MN∥AB;②∠DPM=60°;③∠DAP=∠PEC;④△ACM≌△DCN;⑤若∠DBE=30°,则∠AEB=90°.2(2023秋·四川凉山·八年级统考期末)如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.求证:(1)AD=BE;(2)△CPQ为等边三角形;3(2021春·广东佛山·八年级校考阶段练习)已知图1是边长分别为a和b a>b的两个等边三角形纸片ABC和三角形C DE叠放在一起(C与C 重合)的图形.(1)将△C DE绕点C按顺时针方向旋转30°,连接AD,BE.如图2:在图2中,线段BE与AD之间具有怎样的大小关系?证明你的结论;(2)若将上图中的△C DE,绕点C按顺时针方向任意旋转一个角度α,连接AD、BE,如图3:在图3中,线段BE与AD之间具有怎样的大小关系?证明你的结论:(3)根据上面的操作过程,请你猜想当α为多少度时,线段AD的长度最大,最大是多少?当α为多少度时,线段AD的长度最小,最小是多少?请直接写出答案.4(2023春·广东梅州·七年级校考期末)【初步感知】(1)如图1,已知ΔABC为等边三角形,点D为边BC上一动点(点D不与点B,点C重合).以AD为边向右侧作等边ΔADE,连接CE.求证:ΔABD≌ΔACE;【类比探究】(2)如图2,若点D在边BC的延长线上,随着动点D的运动位置不同,猜想并证明:①AB与CE的位置关系为:;②线段EC、AC、CD之间的数量关系为:;【拓展应用】(3)如图3,在等边ΔABC中,AB=3,点P是边AC上一定点且AP=1,若点D为射线BC上动点,以DP为边向右侧作等边ΔDPE,连接CE、BE.请问:PE+BE是否有最小值?若有,请直接写出其最小值;若没有,请说明理由.【类型二共顶点的等腰直角三角形】1(2023春·湖北黄冈·八年级统考期中)如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE= 90°.(1)【猜想】:如图1,点E在BC上,点D在AC上,线段BE与AD的数量关系是,位置关系是.(2)【探究】:把△DCE绕点C旋转到如图2的位置,连接AD,BE,(1)中的结论还成立吗?说明理由;(3)【拓展】:把△DCE绕点C在平面内自由旋转,若AC=5,CE=22,当A,E,D三点在同一直线上时,则AE的长是.【变式训练】1(2023·全国·九年级专题练习)如图,在等腰直角三角形ABC和DEC中,∠BCA=∠DCE=90°,点E在边AB上,ED与AC交于点F,连接AD.(1)求证:△BCE≌△ACD;(2)求证:AB⊥AD.2(2023春·八年级课时练习)(1)问题发现:如图1,△ABC与△CDE均为等腰直角三角形,∠ACB=∠DCE=90°,则线段AE、BD的数量关系为,AE、BD所在直线的位置关系为;(2)深入探究:在(1)的条件下,若点A,E,D在同一直线上,CM为△DCE中DE边上的高,请判断∠ADB的度数及线段CM,AD,BD之间的数量关系,并说明理由.3(2023·山东枣庄·统考二模)感知:如图①,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE =90°,点B在线段AD上,点C在线段AE上,我们很容易得到BD=CE,不需证明.(1)探究:如图②,将△ADE绕点A逆时针旋转α(0<α<90°),连接BD和CE,此时BD=CE是否依然成立?若成立,写出证明过程;若不成立,说明理由.(2)应用:如图③,当△ADE绕点A逆时针旋转,使得点D落在BC的延长线上,连接CE.求:①∠ACE的度数;②若AB=AC=32,CD=3,则线段DE的长是多少?【类型三共顶点的一般等腰三角形】1(2023春·山东泰安·七年级校考开学考试)如图,△ABC与△CDE都是等腰三角形,AC=BC,CD= CE,∠ACB=∠DCE=42°,AD、BE相交于点M.(1)试说明:AD=BE;(2)求∠AMB的度数.【变式训练】1(2023秋·辽宁抚顺·八年级统考期末)如图,已知△ABC中,AB≠AC≠BC.分别以AB、AC为腰在AB左侧、AC右侧作等腰三角形ABD.等腰三角形ACE,连接CD、BE.(1)如图1,当∠BAD=∠CAE=60°时,①△ABD、△ACE的形状是;②求证:BE=DC.(2)若∠BAD=∠CAE≠60°,①如图2,当AB=AD,AC=AE时,BE=DC是否仍然成立?请写出你的结论并说明理由;②如图3,当AB=DB,AC=EC时,BE=DC是否仍然成立?请写出你的结论并说明理由.2(2023秋·全国·八年级专题练习)定义:顶角相等且顶点重合的两个等腰三角形叫做“同源三角形”,我们称这两个顶角为“同源角”.如图,△ABC和△CDE为“同源三角形”,AC=BC,CD=CE,∠ACB 与∠DCE为“同源角”.(1)如图1,△ABC和△CDE为“同源三角形”,试判断AD与BE的数量关系,并说明理由.(2)如图2,若“同源三角形”△ABC和△CDE上的点B,C,D在同一条直线上,且∠ACE=90°,则∠EMD =°.(3)如图3,△ABC和△CDE为“同源三角形”,且“同源角”的度数为90°时,分别取AD,BE的中点Q,P,连接CP,CQ,PQ,试说明△PCQ是等腰直角三角形.3(2023春·辽宁丹东·七年级统考期末)(1)如图1,两个等腰三角形△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,连接BD,CE.则△ADB≌,此时线段BD和线段CE的数量关系式;(2)如图2,两个等腰直角三角形△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连接BD,CE,两线交于点P,请判断线段BD和线段CE的关系,并说明理由;(3)如图3,分别以△ABC的两边AB,AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,两线交于点P.请直接写出线段BE和线段CD的数量关系及∠PBC+∠PCB的度数.。
共顶点的等腰三角形问题课件PPT

基本了解这本书的内容,然后再决定是否值得去读。
变式题
感谢观看
∵AC=BC ∴BC=EF ∴BC-FC=EF-FC 即BF=CE ∴BF=FD ∴△BFD是等腰直角三角形 ∴∠DBE=45°.
典例精解
类型二:共顶点的等边三角形
如图所示,△ACM和△BCN都为等边三角形,连接AN、BM,求证:
AN=BM.
N M
A
1
2 3
B
C
证明: ∵△ACM和△BCN都为等边三角形, ∴∠1=∠3=60° ∴∠1+∠2=∠3+ ∠2 即∠ACN=∠MCB ∵CA=CM,CB=CN ∴△CAN≌△CMB(SAS) ∴AN=BM
03
的短文来进行群读,训练自己一次扫视3~5个字或词。
经常进行这样训练,快速阅读速度就能大大提高。
变式题
以跳读的方式翻阅全书
优翼微课
当拿到一本书时,我们不要一页一页地去翻,要先看书的
初中数学知识点精讲课程 标题和副标题、作者和出版者、编者的话和关于作者的说
明;然后浏览目录,阅读内容提要、前言或后记;最后,以跳读
变式题
刘峻琳同学的阅读习惯非常好,有快读有慢读, 既保证了一定的阅读速度,同时也没有落下重点。 下面我们来介绍另外一种快速阅读法。这种方法 由美国教育学家比尔·科斯比和前苏联著名学者 奥库兹涅佐夫等人提出,并在实践中不断丰富和 完善。
快速阅读有三种表现方式
1.跃式阅读。读书时不要逐句逐段,而是跳跃式的,
课堂小结
如果两个等腰三角形共顶点且顶角相等,那么将两条腰分配到不同的两个 三角形中会得到全等三角形,并且我们会发现:改变两个三角形的相对位置并 不会改变所得的三角形的全等关系.
人教版八年级数学上册7.模型构建专题:共顶点的等腰三角形
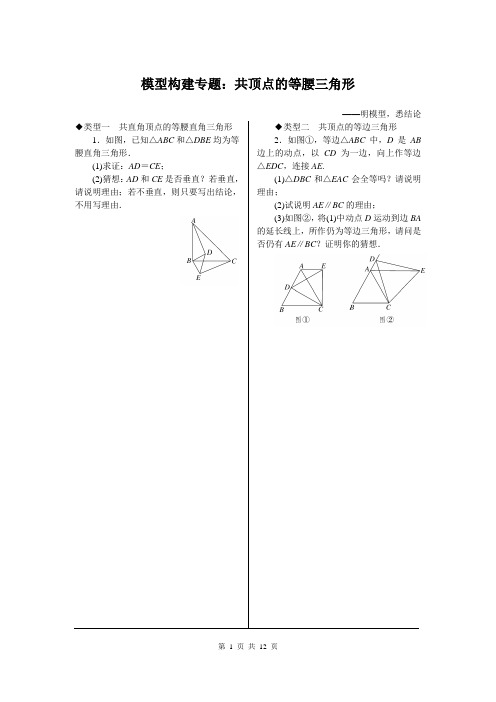
模型构建专题:共顶点的等腰三角形◆类型一共直角顶点的等腰直角三角形1.如图,已知△ABC和△DBE均为等腰直角三角形.(1)求证:AD=CE;(2)猜想:AD和CE是否垂直?若垂直,请说明理由;若不垂直,则只要写出结论,不用写理由.◆类型二共顶点的等边三角形2.如图①,等边△ABC中,D是AB 边上的动点,以CD为一边,向上作等边△EDC,连接AE.(1)△DBC和△EAC会全等吗?请说明理由;(2)试说明AE∥BC的理由;(3)如图②,将(1)中动点D运动到边BA 的延长线上,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.参考答案与解析1.(1)证明:∵△ABC和△DBE均为等腰直角三角形,∴AB=BC,BD=BE,∠ABC=∠DBE=90°,∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE,∴△ABD≌△CBE(SAS),∴AD=CE.(2)解:垂直.理由如下:如图,延长AD分别交BC和CE于G和F.∵△ABD≌△CBE,∴∠BAD=∠BCE.∵∠BAD+∠ABC+∠BGA=∠BCE+∠AFC+∠CGF=180°,∠BGA=∠CGF,∴∠AFC=∠ABC=90°,∴AD⊥CE.2.解:(1)△DBC和△EAC全等.理由如下:∵△ABC和△EDC为等边三角形,∴BC=AC,DC=EC,∠ACB=∠DCE=60°,∴∠ACB-∠ACD=∠DCE-∠ACD,即∠BCD=∠ACE,∴△DBC≌△EAC(SAS).(2)∵△DBC≌△EAC,∴∠EAC=∠B =60°.又∵∠ACB=60°,∴∠EAC=∠ACB,∴AE∥BC.(3)仍有AE∥BC.证明如下:∵△ABC,△EDC为等边三角形,∴BC=AC,DC=CE,∠BCA=∠DCE=60°,∴∠BCA+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE.在△DBC和△EAC中,∵⎩⎪⎨⎪⎧BC=AC,∠BCD=∠ACE,CD=CE,∴△DBC≌△EAC(SAS),∴∠EAC=∠B=60°.又∵∠ACB=60°,∴∠EAC=∠ACB,∴AE∥BC.。
人教版初中数学八上小专题(十二) “手拉手”模型问题——共顶点的等腰三角形(教材P83习题T12变式

(2)判断BD,CE之间的关系并证明;
(2)解:BD=CE且BD⊥CE.证明如下: 设BD交AC于点F. 由(1)知△ABD≌△ACE, ∴BD=CE,∠ABD=∠ACE. ∵∠BFA=∠CFP,∴∠BPC=∠BAC=90°, ∴BD⊥CE.
(3)连接PA,求∠APB的度数.
类型二 共顶点的等边三角形 2.如图,△ABC,△CDE均为等边三角形,连接BD,AE交于点O,BC与AE交于点
(2)求∠APB的度数;(用含α的式子表示) 图1
(3)解:如图,点P即为所求. 图2
类型三 共顶点的一般双等腰三角形 3.如图1,AB=AC,AD=AE,∠BAC=∠DAE=α,连接BD,CE交于点P,连接
AP.
(1)求证:BD=CE;
图1
(1)证明:Leabharlann ∠BAC=∠DAE,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE.
∵AB=AC,AD=AE,∴△BAD≌△CAE(SAS),∴BD=CE.
P.求证:∠AOB=60°. 证明:∵△ABC,△CDE均为等边三角形, ∴AC=BC,CD=CE,∠ACB=∠DCE=60°, ∴∠ACB+∠BCE=∠DCE+∠BCE, 即∠ACE=∠BCD, ∴△ACE≌△BCD(SAS),∴∠CAE=∠CBD. ∵∠APC=∠BPO, ∴∠BOP=∠ACP=60°,即∠AOB=60°.
小专题(十二) “手拉手”模型问题——共顶点的等腰三角形
(教材P83习题T12变式)
类型一 共顶点的等腰直角三角形 1.如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,连接BD,
CE交于点P. (1)求证:△ABD≌△ACE;
(1)证明:∵△ABC和△ADE均为等腰直角三角形, ∴AB=AC,AD=AE. ∵∠BAC=∠DAE=90°, ∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE, ∴△ABD≌△ACE(SAS).
共顶点的等腰三角形问题课件

边长性质
总结词
共顶点的等腰三角形具有特定的边长关系,即两腰相等,底 边与其中一腰不等。
详细描述
由于是等腰三角形,两腰的长度必然相等。而共顶点的两个 等腰三角形共享一个顶点,因此它们的边长关系也是固定的 。具体来说,两腰相等,而底边与其中一腰的长度不等。
面积性质
总结词
共顶点的等腰三角形具有特定的面积关系,即两个等腰三角形的面积之和等于以底边为基的三角形的 面积。
02
等腰三角形两腰之间的角称为顶 角,底边与两腰之间的角称为底 角。
共顶点的等腰三角形的特性
共顶点的等腰三角形是指两个或多个 等腰三角形共用一个顶点,且各等腰 三角形的腰和底边分别相等。
共顶点的等腰三角形具有轴对称性, 即沿对称轴对折后,两侧图形能够完 全重合。
共顶点的等腰三角形的分类
根据共顶点的等腰三角形的数量,可分为双共顶点的等腰三角形和多共顶点的等 腰三角形。
共顶点的等腰三角形 问题课件
目录
• 共顶点的等腰三角形的基本概念 • 共顶点的等腰三角形的性质 • 共顶点的等腰三角形的构造方法 • 共顶点的等腰三角形的应用 • 共顶点的等腰三角形的习题与解析
01
共顶点的等腰三角形的基本概念
等腰三角形的定义
01
等腰三角形是两边长度相等的三 角形,其中两个等长的边称为腰 ,另一边称为底边。
高难度习题
题目5
已知等腰三角形ABC,AB=AC,D为BC延长线上一点 ,E、F为AD上两点,且∠BEC=160°,∠BDC=5°。求 ∠EDF的度数。
题目6
已知等腰三角形ABC,AB=AC,D为BC延长线上一点 ,E、F、G为AD上三点,且∠BEC=170°,∠BDC=10° 。求∠DEFG的度数。
人教版八年级上册模型构建专题共顶点的等腰三角形
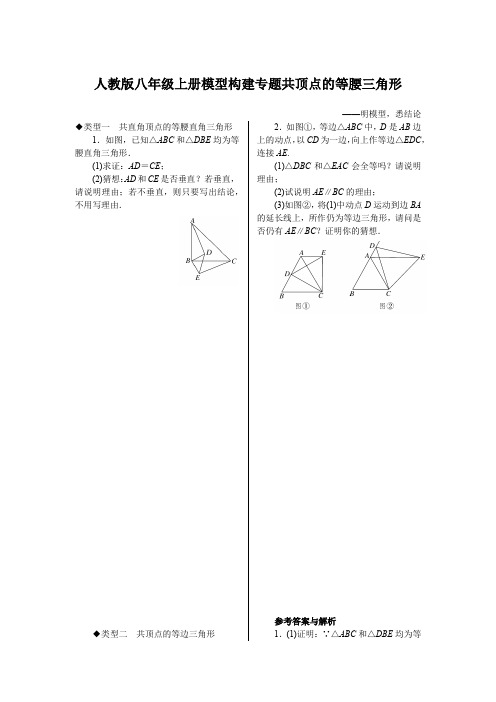
人教版八年级上册模型构建专题共顶点的等腰三角形——明模型,悉结论◆类型一共直角顶点的等腰直角三角形1.如图,已知△ABC和△DBE均为等腰直角三角形.(1)求证:AD=CE;(2)猜想:AD和CE是否垂直?若垂直,请说明理由;若不垂直,则只要写出结论,不用写理由.◆类型二共顶点的等边三角形2.如图①,等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.(1)△DBC和△EAC会全等吗?请说明理由;(2)试说明AE∥BC的理由;(3)如图②,将(1)中动点D运动到边BA 的延长线上,所作仍为等边三角形,请问是否仍有AE∥BC?证明你的猜想.参考答案与解析1.(1)证明:∵△ABC和△DBE均为等腰直角三角形,∴AB =BC ,BD =BE ,∠ABC =∠DBE =90°,∴∠ABC -∠DBC =∠DBE -∠DBC ,即∠ABD =∠CBE ,∴△ABD ≌△CBE (SAS),∴AD =CE .(2)解:垂直.理由如下:如图,延长AD 分别交BC 和CE 于G 和F .∵△ABD ≌△CBE ,∴∠BAD =∠BCE .∵∠BAD +∠ABC +∠BGA =∠BCE +∠AFC +∠CGF =180°,∠BGA =∠CGF ,∴∠AFC =∠ABC =90°,∴AD ⊥CE .2.解:(1)△DBC 和△EAC 全等.理由如下:∵△ABC 和△EDC 为等边三角形,∴BC =AC ,DC =EC ,∠ACB =∠DCE =60°,∴∠ACB -∠ACD =∠DCE -∠ACD ,即∠BCD =∠ACE ,∴△DBC ≌△EAC (SAS).(2)∵△DBC ≌△EAC ,∴∠EAC =∠B =60°.又∵∠ACB =60°,∴∠EAC =∠ACB ,∴AE ∥BC .(3)仍有AE ∥BC .证明如下:∵△ABC ,△EDC 为等边三角形,∴BC =AC ,DC =CE ,∠BCA =∠DCE =60°,∴∠BCA +∠ACD =∠DCE +∠ACD ,即∠BCD =∠ACE .在△DBC 和△EAC 中,∵⎩⎪⎨⎪⎧BC =AC ,∠BCD =∠ACE ,CD =CE ,∴△DBC ≌△EAC (SAS),∴∠EAC =∠B =60°.又∵∠ACB =60°,∴∠EAC =∠ACB ,∴AE ∥BC .。
模型构建:“手拉手”模型——共顶点的等腰三角形压轴题三种模型全攻略(解析版)

专题12模型构建专题:“手拉手”模型——共顶点的等腰三角形压轴题三种模型全攻略【考点导航】目录【典型例题】 (1)【类型一共顶点的等边三角形】 (1)【类型二共顶点的等腰直角三角形】 (10)【类型三共顶点的一般等腰三角形】 (17)【典型例题】【类型一共顶点的等边三角形】例题:(2023春·陕西西安·八年级西北大学附中校考阶段练习)如图所示,A 、C 、B 三点在同一条直线上,DAC △和EBC 都是等边三角形,AE 、BD 交于点P ,且分别与CD 、CE 交于点M ,N ,证明:(1)ACE DCB △△≌;(2)CM CN ;(3)60APD ∠=︒.【答案】(1)证明见解析(2)证明见解析(3)证明见解析【分析】(1)根据等边三角形的性质和全等三角形的判定证明即可;(2)先证明EMC BNC ≌ ,根据全等三角形的性质即可证明;(3)由三角形内角和定理可得APD ACM ∠=∠,即可证明.【详解】(1)证明:∵DAC △和EBC 都是等边三角形,∴AC CD =,CE BC =,60ACD ECB ∠=∠=︒,∴ACE DCB ∠=∠,在ACE △与DCB △中,AC CD ACE DCB CE BC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ACE DCB ≌ ;(2)∵ACE DCB △△≌,∴AEC DBC ∠=∠,∵180DCE ACD ECB ∠+∠+∠=︒,60ACD ECB ∠=∠=︒,∴60DCE ECB ∠=∠=︒,∵CE BC =,60DCE ECB ∠=∠=︒,AEC DBC ∠=∠,在EMC △与BNC 中,DCE ECB CE BC AEC DBC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()ASA EMC BNC ≌ ,∴CM CN =;(3)∵180MDP DMP APD MAC AMC ACM ∠+∠+∠=∠+∠+∠=︒,又∵MDP MAC∠=∠∴60APD ACM ∠=∠=︒.【点睛】本题考查了等边三角形的性质及全等三角形的判定方法,关键是根据等边三角形的性质解答.【变式训练】【答案】(1)(2)(4)【分析】根据ABC 与CDE ACE BCD ∠=∠,可证ACE 的度数时,BCE ∠的度数也会发生变化,同时也会出现∵AGC BGF ∠=∠,CBD ∠∴60BFA ACB Ð=Ð=°;(1)如图1,若BD AD⊥.①求CED∠的度数;=;②延长ED交BC于点F,求证:BF CF(2)如图2,若点D在边AC上,延长BD交CE于点60AB AC AD AE BAC DAE AED ∴==∠=∠=∠=︒,,,BAD CAE ∴∠=∠,∴()SAS ABD ACE ≌△△,∴ADB AEC ∠=∠,∵BD AD ⊥,∴90AEC ADB ∠=∠=︒,又∵60AED ∠=︒,∴30CED AEC AED ∠=∠-∠=︒,∴CED ∠为30︒.②证明:如图1,过点C 作CH BD ∥,交EF 的延长线于点H ,则H BDF ∠=∠,由①知,906030AEC ADB ADE AED CEH ∠=∠=︒∠=∠=︒∠=︒,,,∴180180906030BDF ADB ADE ∠=︒-∠-∠=︒-︒-︒=︒,∴BDF CEH ∠=∠,∴H CEH ∠=∠,∴CH CE =,∵()SAS ABD ACE ≌△△,∴BD CE =,∴BD CH =,又∵BFD CFH ∠=∠,BDF H ∠=∠,∴()AAS BDF CHF △≌△,∴BF CF =.(2)证明:如图2,过点A 分别作AP BG ⊥于点P ,AP BG ⊥于点Q ,AB AC BAD CAE =∠=∠ ,∴()SAS ABD ACE ≌△△∴BD CE =,ABD ACE S S = ∵AP BG ⊥,AQ CE ⊥,(1)将C DE ' 绕点C 按顺时针方向旋转30︒,连接AD ,BE .如图2:在图样的大小关系?证明你的结论;(2)若将上图中的C DE ' ,绕点C 按顺时针方向任意旋转一个角度α,连接线段BE 与AD 之间具有怎样的大小关系?证明你的结论:(3)当α为180度时,线段AD 的长度最大,最大值为a b +;当α为0度或360度时,线段AD 的长度最小,最小值为a b -.【分析】(1)先由等边三角形判断出AC BC =,CE CD =,再由旋转判断出BCE ACD ∠=∠,进而判断出BCE ACD ≌,即可得出结论;(2)同(1)的方法,即可得出结论;(3)当点D 在AC 的延长线上时,AD 最大,最大值为a b +,当点D 在线段AC 上时,AD 最小,最小值为a b -,即可得出结论.【详解】(1)解:BE AD=证明: 点C 与1C 重合,ABC 和1C DE △,ABC ∴ 和CDE 都是等边三角形,AC BC ∴=,CE CD =,由旋转知,30BCE ACD ∠=∠=︒,在BCE 和ACD 中,BC AC BCE ACD CE CD =⎧⎪∠=∠⎨⎪=⎩,(SAS)BCE ACD ∴≌△△,BE AD ∴=,(2)解:BE AD =,证明:ABC 和CDE 都是等边三角形,AC BC ∴=,CE CD =,由旋转知,BCE ACD ∠=∠,在BCE 和ACD 中,BC AC BCE ACD CE CD =⎧⎪∠=∠⎨⎪=⎩,(SAS)BCE ACD ∴≌△△,BE AD ∴=;(3)解:当点D 在AC 的延长线上时,AD 最大,最大值为AC CD a b +=+,如图,∴当α为180度时,线段AD 的长度最大,最大值为a b +,当点D 在线段AC 上时,AD 最小,最小值为AC CD a b -=-,如图,∴当α为0度或360度时,线段AD 的长度最小,最小值为a b -.【点睛】此题是三角形综合题,主要考查了等边三角形的性质,全等三角形的判定和性质,判断出BCE ACD ≌是解本题的关键.4.(2023春·山西临汾·八年级统考期末)综合与实践特例感知:如图1,在等边三角形ABC 中,D 是BC 延长线上一点,且CD BC <,以CD 为边作等边三角形CDE ,连接BE ,分别过点B 作BF ED ∥,过点D 作DF BE ∥,交于点F ,连接AF AC ,与BE 交于点G .(1)试判断AF 和BE 的数量关系,并说明理由.(2)猜想论证:将CDE 绕点C 按顺时针方向旋转一定角度得到图2,则(1)中AF 和BE 的数量关系是否仍然成立?请说明理由.(3)拓展延伸:将如图1所示的CDE 绕点C 按逆时针方向旋转角度()0180αα︒<<︒,当90ABF ∠=︒时,请直接写出α的值.【答案】(1)AF BE =,理由见解析(2)(1)中AF 和BE 的数量关系仍然成立,理由见解析(3)α的值为30︒【分析】(1)根据等边三角形的性质和SAS 证明ABF BCE ≌,进而利用全等三角形的性质解答即可;(2)延长BC ,交ED 于点M ,根据等边三角形的性质和SAS 证明ABF BCE ≌,进而利用全等三角形的性质解答即可;(3)利用(2)中的结论解答即可.【详解】(1)解:AF BE =,理由:ABC 和CDE 都是等边三角形,60AB BC CE ED ABC ECD EDC ∴==∠=∠=∠=︒,,,180120BCE ECD ∴∠=︒-∠=︒,DF BE BF ED ∥,∥,∴四边形BFDE 是平行四边形,BF ED ∴=,60FBD EDC ∠=∠=︒,BF CE ∴=,120ABF ABC FBD ∠=∠+∠=︒ ,180120BCE ECD ∠=︒-∠=︒,ABF BCE ∴∠=∠,ABF BCE ∴ ≌,AF BE ∴=;(2)解:仍然成立,理由:如图,延长BC ,交ED 于点M ,,ABC 和CDE 都是等边三角形,60AB BC CE ED ABC ECD EDC ∴==∠=∠=∠=︒,,,E BF D ∥Q ,FBM BME ∴∠=∠,60ABF ABC FBM FBM ∠=∠+∠=︒+∠ ,60BCE CEM CME BME ∠=∠+∠=︒+∠,ABF BCE ∴∠=∠,同(1)可知,BF CE =,()SAS ABF BCE ∴ ≌,AF BE ∴=;(3)解:当90ABF ∠=︒时,如图,,由(2)可知,ABF BCE ∠=∠,90BCE ∴∠=︒,60ECD ∠=︒ ,18030BCE ECD α∴=︒-∠-∠=︒,∴α的值为30︒.【点睛】本题主要考查了三角形全等的判定及性质、等边三角形的性质,熟练掌握三角形全等的判定及性质、等边三角形的性质,添加适当的辅助线,是解题的关键.【类型二共顶点的等腰直角三角形】例题:(2023秋·山东泰安·七年级统考期末)如图,已知ABC 和DBE 均为等腰直角三角形,且90ABC DBE ︒∠=∠=(1)试说明:AD CE=(2)试判断AD 和CE 的位置关系,并说明理由.【答案】(1)见解析(2)AD CE ⊥,理由见解析【分析】(1)由等腰直角三角形的性质得出AB BC =,BD BE =,90ABC DBE ︒∠=∠=,得出ABD CBE ∠=∠,证出ABD CBE ≌,即可得出AD CE=(2)ABD CBE ≌得出BAD BCE ∠=∠,再由180BAD ABC BGA BCE AFC CGF ︒∠+∠+∠=∠+∠+∠=,得90AFC ABC ︒∠=∠=,即可证出结论【详解】(1)∵ABC 和DBE 是等腰直角三角形,∴AB BC =,BD BE =,90ABC DBE ︒∠=∠=,∵.ABC DBC DBE DBC ∠-∠=∠-∠,即ABD CBE ∠=∠,在ABD △和CBE △中,AB BC =,BD BE =,ABD CBE∠=∠∴ABD CBE≌∴AD CE=(2)延长AD 分别交BC 和CE 于G 和F ,如图所示:∵ABD CBE ≌,∴BAD BCE ∠=∠,∵180BAD ABC BGA BCE AFC CGF ︒∠+∠+∠=∠+∠+∠=,∵BGA CGF ∠=∠,∵180BAD ABC BGA BCE AFC CGF ︒∠+∠+∠=∠+∠+∠=,∴90AFC ABC ︒∠=∠=,∴AD CE⊥【点睛】本题考查了等腰直角三角形的性质和全等三角形的判定与性质;证明三角形全等是解决问题的关键【变式训练】1.(2023春·全国·八年级专题练习)ABC 和△ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒.(1)如图1,点D 、E 在AB ,AC 上,则BD ,CE 满足怎样的数量关系和位置关系?(直接写出答案不证明)(2)如图2,点D 在ABC 内部,点E 在ABC 外部,连接BD ,CE ,则BD ,CE 满足怎样的数量关系和位置关系?请说明理由.【答案】(1)BD CE =,BD CE⊥(2)BD CE =,BD CE ⊥,理由见解析【分析】(1)根据等腰直角三角形结合线段的和差即可得到结论;(2)延长BD ,分别交AC 、CE 于F 、G ,证明ABD ACE ≌△△,根据全等三角形的性质、垂直的定义解答;【详解】(1)解:∵ABC 和△ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,∴AB AC =,AD AE =,∴AB AD AC AE -=-,即BD CE =,∵点D ,E 在AB ,AC 上,AD AC ⊥,∴BD CE ⊥;(2)BD CE =,BD CE ⊥,理由如下:延长BD ,分别交AC 、CE 于F 、G ,∵ABC 和△ADE 都是等腰直角三角形,90BAC DAE ∠=∠=︒,∴AB AC =,AD AE =,∵BAD BAC DAC ∠=∠-∠,CAE DAE DAC ∠=∠-∠,∴BAD CAE ∠=∠,在ABC 和ADE V 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴ABD ACE ≌△△,∴BD CE =,ABD ACE ∠=∠,∵A F B G F C ∠=∠,180AFB ABD BAC GFC ACE CGF ∠+∠+∠=∠+∠+∠=︒,∴90CGF BAF ∠=∠=︒,即BD CE ⊥;【点睛】本题是三角形综合题,主要考查的是等腰直角三角形的性质、全等三角形的判定和性质,掌握相关的判定定理和性质定理是解题的关键.2.(2023秋·山东滨州·八年级统考期末)如图,ABD △和ACE △都是等腰直角三角形,且90DAB EAC ∠=∠=︒,CD 与BE 交于点O ,(1)求证:BE CD =;(2)求证:BE CD ⊥.【答案】(1)见解析(2)见解析【分析】(1)先证明CAD BAE ∠=∠,进而证明()SAS ABE ADC ∠≌△,根据全等三角形的性质即可得证;(2)设CA 、BE 交于N ,根据ABE ADC △≌△得出ACD AEB ∠=∠,进而根据三角形内角和定理即可得证.【详解】(1)解:在ABD △和ACE △中,AB AD =,AC AE =,=90BAD CAE ∠=∠︒,∴BAD BAC CAE BAC ∠+∠=∠+∠,即CAD BAE ∠=∠,∵在ABE 和ADC △中AB AD BAE DAC AE AC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABE ADC ∠≌△,∴BE CD =;(2)设CA 、BE 交于N ,∵ABE ADC △≌△,∴ACD AEB ∠=∠,∵ANE CNO ∠=∠,180ANE NAE AEN ∠+∠+∠=︒,180ONC NOC OCN ∠+∠+∠=︒,∴90NOC NAE ∠=∠=︒,∴BE CD ⊥.【点睛】本题考查了全等三角形的性质与判定,三角形内角和定理的应用,等腰三角形的性质,掌握全等三角形的性质与判定是解题的关键.3.(2023春·全国·七年级专题练习)ABC 与BDE △均为等腰直角三角形,90ABC DBE ∠=∠=︒.(1)如图1,当D ,B ,C 在同一直线时,CE 的延长线与AD 交于点F .求证:90CFA ∠=︒;(2)当ABC 与BDE △的位置如图2时,CE 的延长线与AD 交于点F ,猜想CFA ∠的大小并证明你的结论;(3)如图3,当A ,E ,D 在同一直线时(A ,D 在点E 的异侧),CE 与AB 交于点G ,BAD ACE ∠=∠,求证:BG AB AC +=.【答案】(1)见解析(2)∠CFA =90°,证明见解析(3)见解析【分析】(1)证明△ABD ≌△CBE (SAS ),由全等三角形的性质得出∠BAD =∠BCE ,由对顶角的性质可得出答结论;(2)同理可证△ABD ≌△CBE (SAS ),得出∠BAD =∠BCE ,则可得出结论;(3)过点G 作GH ⊥AC 于点H ,同(2)可知∠BAD =∠BCE ,证出BG =GH ,证明Rt △BCG ≌Rt △HCG (HL ),由全等三角形的性质得出BC =CH ,则得出结论.【详解】(1)证明:∵△ABC 和△DBE 是等腰直角三角形,∴AB =BC ,BD =BE ,∠ABC =∠DBE =90°,在△ABD 和△CBE 中,AB BC ABD CBE BD BE ⎧⎪∠∠⎨⎪⎩===,∴△ABD ≌△CBE (SAS ),∴∠BAD =∠BCE ,∵∠BAD +∠AFE +∠FEA =∠BCE +∠ABC +∠BEC =180°,又∵∠FEA =∠BEC ,∴∠CFA =∠ABC =90°.(2)解:∠CFA =90°.理由如下:同理可证△ABD ≌△CBE (SAS ),∴∠BAD =∠BCE ,∴∠CFA =∠ABC =90°.(3)过点G 作GH ⊥AC 于点H ,同(2)可知∠BAD =∠BCE ,∵∠BAD =∠ACE ,∴∠ACE =∠BCE ,∵AB ⊥BC ,GH ⊥AC ,∴BG =GH ,∵∠BAC =45°,∴∠BAC =∠AGH =45°,∴GH =AH ,∴AH =BG ,在Rt △BCG 和Rt △HCG 中CG CG BG HG⎧⎨⎩==,∴Rt △BCG ≌Rt △HCG (HL ),∴BC =CH ,∴AC =AH +CH =BG +BC =BG +AB .【点睛】本题是三角形综合题,考查了三角形内角和定理,等腰直角三角形的性质和全等三角形的判定与性质;证明三角形全等是解决问题的关键.【类型三共顶点的一般等腰三角形】例题:(2023秋·四川遂宁·八年级统考期末)新定义:顶角相等且顶角顶点重合的两个等腰三角形互为“兄弟三角形”.(1)如图①中,若ABC 和ADE 互为“兄弟三角形”,AB AC =,AD AE =.则①BAD ∠___________CAE ∠(填>、<或=)②连接线段BD 和CE ,则BD ___________CE (填>、<或=)(2)如图②,ABC 和ADE 互为“兄弟三角形”,AB AC =,AD AE =,若点D 、点E 均在ABC 外,连接BD 、CE 交于点M ,连接AM ,则线段BD CE 、还满足以上数量关系吗?请说明理由【答案】(1)①=,②=(2)BD CE =,见解析【分析】(1)根据“兄弟三角形”的定义可知两个三角形的顶角相等,利用角的和差即可得到①的结论;再结合“SAS ”即可得到BAD ≌CAE V ,根据全等三角形的性质即可求解;(2)沿用(1)的思路,利用角的和差得到BAD CAE ∠=∠,再结合“SAS ”即可得到()SAS BAD CAE ≌△△,根据全等三角形的性质即可求解.【详解】(1)①BAD CAE ∠=∠;∵ABC 和△ADE 互为“兄弟三角形”,AB AC =,AD AE =,∴BAC DAE ∠=∠,∴BAC DAC DAE DAC ∠-∠=∠-∠,即BAD CAE ∠=∠;②BD CE =;在BAD 和CAE V 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BAD CAE ≌△△,∴BD CE =.(2)满足以上关系证明:如图②,∵ABC 和△ADE 互为“兄弟三角形”,∴BAC DAE ∠=∠,∴BAC DAC DAE DAC ∠+∠=∠+∠,即CAE BAD ∠=∠,在BAD 和CAE V 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BAD CAE ≌△△,∴BD CE =.【点睛】本题考查全等三角形的性质与判定,根据题目信息识别出来全等三角形是解题的关键.【变式训练】1.(2023春·山东泰安·七年级校考开学考试)如图,ABC 与CDE 都是等腰三角形,42AC BC CD CE ACB DCE AD BE ==∠=∠=︒,,,、相交于点M .(1)试说明:AD BE =;(2)求AMB ∠的度数.【答案】(1)见解析(2)42︒【分析】(1)由“SAS ”可证≌ACD BCE V V ,可得BE AD =;(2)根据全等三角形的性质可得CAD CBE ∠=∠,再利用三角形内角和定理计算AMB ∠.【详解】(1)解:证明:ACB DCE ∠=∠ ,ACD BCE ∠∠∴=,在ACD 和BCE 中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩,(SAS)ACD BCE ∴≌△△,AD BE ∴=;(2)ACD BCE ≌,CAD CBE ∴∠=∠,18042138BAC ABC ∠+∠=︒-︒=︒ ,138BAM ABM BAC CAD ABC CBE BAC ABC ∴∠+∠=∠-∠+∠+∠=∠+∠=︒,18013842AMB ∴∠=︒-︒=︒.【点睛】本题考查了全等三角形的判定和性质,三角形内角和,证明三角形全等是解题的关键.2.(2023秋·辽宁抚顺·八年级统考期末)如图,已知ABC 中,AB AC BC ≠≠.分别以AB 、AC 为腰在AB 左侧、AC 右侧作等腰三角形ABD .等腰三角形ACE ,连接CD 、BE .(1)如图1,当60BAD CAE ∠=∠=︒时,①ABD △、ACE △的形状是____________;②求证:BE DC =.(2)若60BAD CAE ∠=∠≠︒,①如图2,当AB AD AC AE ==,时,BE DC =是否仍然成立?请写出你的结论并说明理由;②如图3,当AB DB AC EC ==,时,BE DC =是否仍然成立?请写出你的结论并说明理由.【答案】(1)①等边三角形;②证明见解析(2)①成立,理由见解析;②不成立,理由见解析【分析】(1)①根据有一个内角是60度的等腰三角形是等边三角形即可求解;②根据等边三角形的性质可得AB AD =,AE AC =,60DAB CAE ∠=∠=︒,证明BAE DAC ≌ ,根据全等三角形的性质即可证明;(2)①证明BAE DAC ≌ ,根据全等三角形的性质即可得出结论;②根据已知可得BAE 与DAC △不全等,即可得出结论.【详解】(1)①∵ABD △是等腰三角形,ACE △是等腰三角形,60BAD CAE ∠=∠=︒∴ABD △、ACE △是等边三角形,故答案为:等边三角形.②证明:∵ABD △、ACE △是等边三角形,∴AB AD =,AE AC =,60DAB CAE ∠=∠=︒,∵DAC DAB BAC ∠=∠+∠,BAE CAE BAC ∠=∠+∠,∴DAC BAE ∠=∠,在△BAE 与△DAC 中,∵AB AD BAE DAC AE AC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS BAE DAC ≌ .∴BE DC =.(2)①当AB AD =,AE AC =时,成立.理由:如图,∵AB AD =,BAE DAC ∠=∠,AE AC =,∴()SAS BAE DAC ≌ ,∴BE DC =;②当AB DB =,AC EC =时,不成立.理由:如图,∵60BAD CAE ∠=∠≠︒,∴AB DB AD =≠,AC EC AE =≠,∴BAE 与DAC △不全等,∴BE DC ≠.【点睛】本题考查全等三角形的判定与性质,等腰三角形的性质,等边三角形的判定与性质等,熟练掌握全等三角形的判定与性质是解题的关键.3.(2023秋·全国·八年级专题练习)定义:顶角相等且顶点重合的两个等腰三角形叫做“同源三角形”,我们称这两个顶角为“同源角”.如图,ABC 和CDE 为“同源三角形”,AC BC =,CD CE =,ACB ∠与DCE ∠为“同源角”.(1)如图1,ABC 和CDE 为“同源三角形”,试判断AD 与BE 的数量关系,并说明理由.(2)如图2,若“同源三角形”ABC 和CDE 上的点B ,C ,D 在同一条直线上,且90ACE ∠=︒,则∠=EMD ______°.(3)如图3,ABC 和CDE 为“同源三角形”,且“同源角”的度数为90°时,分别取AD ,BE 的中点Q ,P ,连接CP ,CQ ,PQ ,试说明PCQ △是等腰直角三角形.【答案】(1)AD BE =,详见解析(2)45(3)详见解析【分析】(1)由“同源三角形”的定义可证ACD BCE ∠=∠,然后根据SAS 证明≌ACD BCE V V 即可;(2)由“同源三角形”的定义和90ACE ∠=︒可求出45DCE ACB ∠==︒,由(1)可知≌ACD BCE V V ,得ADC BEC ∠∠=,然后根据“8”子三角形即可求出EMD ∠的度数;(3)由(1)可知≌ACD BCE V V ,可得CAQ CBP ∠=∠,BE AD =.根据SAS 证明ACQ BCP △≌△,可得CQ CP =,ACQ BCP ∠=∠,进而可证结论成立.【详解】(1)AD BE =.理由:因为ABC 和CDE 是“同源三角形”,所以ACB DCE ∠=∠,所以ACD BCE ∠=∠.在ACD 和BCE 中,,,,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩所以()SAS ACD BCE △≌△.所以AD BE =.(2)∵ABC 和CDE 是“同源三角形”,∴ACB DCE ∠=∠.∵90ACE ∠=︒,∴45DCE ACB ∠==︒.由(1)可知≌ACD BCE V V ,∴ADC BEC ∠∠=.∵MOE COD ∠=∠,∴45EMD DCE ∠=∠=︒.故答案为:45;(3)由(1)可知≌ACD BCE V V ,所以CAQ CBP ∠=∠,BE AD =.因为AD ,BE 的中点分别为Q ,P ,所以AQ BP =.在ACQ 和BCP 中,,,,CA CB CAQ CBP AQ BP =⎧⎪∠=∠⎨⎪=⎩所以()SAS ACQ BCP △≌△,所以CQ CP =,ACQ BCP ∠=∠.又因为90BCP PCA ︒∠+∠=,所以90ACQ PCA ︒∠+∠=.所以90PCQ ∠=︒,所以PCQ △是等腰直角三角形.【点睛】本题考查了新定义,全等三角形的判定与性质,等腰直角三角形的判定,三角形内角和定理等知识,熟练掌握全等三角形的判定与性质是解答本题的关键.。
