新课标人教A版高中数学必修五典题精讲(34基本不等式)
基本不等式人教A版高中数学必修五PPT课件

函数的最小值为 4.
用均值不等式求最值,必须注意 “相等” 的条件. 如果取等的条件不成立,则不能取到该最值.
基本不等式人教A版高中数学必修五PP T课件
基本不等式人教A版高中数学必修五PP T课件
练习
1、若x 0,求f ( x) 12 3x的最小值 x
2、已知x 0,y 0,求证 x y 2 yx
基本不等式人教A版高中数学必修五PP T课件
2.基本不等式 基本不等式人教A版高中数学必修五PPT课件 (均值定理)
如果a 0, b 0,那么 a b ab 2
(当且仅当a b时,取""号)
我们把 a b 叫做正数a, b的算术平均数, 2
把 ab叫做正数a, b的几何平均数。
此定理又可叙述为:
解:∵ x 0
x
x 1 2 x 1 2
x
x
当且仅当x 1 ,即x 1时,原式有最小值 2 x
变式、已知x 0,求x 1 的最值 x
解:∵ x 0, x 0
x 1 [( x) 1 ] 2 ( x) 1 2
x
( x)
( x)
运用均当且值仅不当等式x 的1过,程即x中,1时a、,b原必式须有最为大“正值 数 2”.
(1)a、b均为正数;
(2)a+b与ab有一个为定值;
(3)等号必须取到。பைடு நூலகம்
以上三个条件缺一不可. “一正”、“二定”、“三相等”。
构造积为定值,利用基本不等式求最值
例1、求函数y 1 x( x 3)的最小值
x3
练习:
已知x 1,求x 1 的最小值以及取得最小 值时x的值 x1
答:最小值是3,取得最小值时x的值为2
高中数学人教A版必修5《基本不等式》PPT

,此时 x 6 。
2
下面几道题的解答可能有错,如果错了, 那么错在哪里?
1.已知函数 f (x) x 1 ,求函数的 最小值和此时x的取值. x
运用均值不等式的过程中,忽略了“正数” 这个条件.
2.已知函数 f (x) x 3 (x 2) , x2
求函数的最小值.
用均值不等式求最值,必须满足“定值”这 个条件.
3.4.1《基本不等式 -均值不等式》
教学目标
• 推导并掌握两个正数的算术平均数不小于它们
的几何平均数这个重要定理;利用均值定理求极 值。了解均值不等式在证明不等式中的简单应用。 • 教学重点: • 推导并掌握两个正数的算术平均数不小于它们的 几何平均数这个重要定理;利用均值定理求极值。 了解均值不等式在证明不等式中的简单应用。
定理:如果a,b∈R,那么a2+b2≥2ab
(当且仅当a=b 时取“=”)
证明: a2 b2 2ab (a b)2
当a b时,(a b)2 0
当a
b时,(a
b)2
0
a2 b2 2ab
1.指出定理适用范围: a,b R
2.强调取“=”的条件: a b
均值定理: 如果a, b∈R+,那么 a b ab
3 求函数y sin 4 其中 (0, ]
sin
2
的最小值。
解:y sin 4 2 sin • 4
sin
sin
4,函数的最小值为4。
用均值不等式求最值,必须注意 “相等” 的条 件.
如果取等的条件不成立,则不能取到该最值.
练习题: 1.已知x>0, y>0, xy=24, 求4x+6y的最小值,
3.我们把不等式 a b ab (a≥0,b≥0)
最新人教版高一数学知识(必修5)专题精讲附解答: 基本不等式
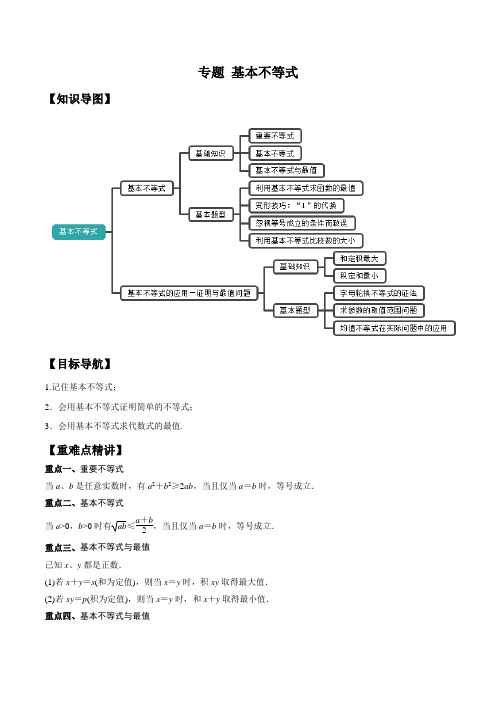
专题基本不等式【知识导图】【目标导航】1.记住基本不等式;2.会用基本不等式证明简单的不等式;3.会用基本不等式求代数式的最值.【重难点精讲】重点一、重要不等式当a、b是任意实数时,有a2+b2≥2ab,当且仅当a=b时,等号成立.重点二、基本不等式当a>0,b>0时有ab≤a+b2,当且仅当a=b时,等号成立.重点三、基本不等式与最值已知x、y都是正数.(1)若x+y=s(和为定值),则当x=y时,积xy取得最大值.(2)若xy=p(积为定值),则当x=y时,和x+y取得最小值.重点四、基本不等式与最值x +y =s (定和)⇒xy ≤s 24(当且仅当x =y 时取等号) xy =p (定积)⇒x +y ≥2p (当且仅当x =y 时取等号)【典题精练】考点1、利用基本不等式求函数的最值例1.函数1(2)2y x x x =+>-的最小值为__________. 【答案】4【解析】∵2x >,∴20x ->.∴111(2)22(2)24222y x x x x x x =+=-++≥-⨯+=--- ,当且仅当122x x -=-,即3x =时等号成立.∴函数1(2)2y x x x =+>-的最小值为4. 答案:4考点点睛:1.利用基本不等式求最值,必须按照“一正,二定,三相等”的原则,即(1)一正:符合基本不等式a +b 2≥ab 成立的前提条件,a >0,b >0; (2)二定:化不等式的一边为定值;(3)三相等:必须存在取“=”号的条件,即“=”号成立.以上三点缺一不可.2.若是求和式的最小值,通常化(或利用)积为定值;若是求积的最大值,通常化(或利用)和为定值,其解答技巧是恰当变形,合理拆分或配凑因式. 考点2、变形技巧:“1”的代换例2.【浙江省七彩联盟2018-2019学年第一学期高三11月期中】若正数a ,b 满足121a b +=,则2b a+的最小值为( )A .42B .82C .8D .9 【答案】D【解析】0a Q >,0b >,且121a b +=, 则2212252549b b a ab a a b ab ⎛⎫⎛⎫+=++=++=≥+= ⎪⎪⎝⎭⎝⎭, 当且仅当22ab ab =即13a =,3b =时取等号. 故选D .考点点睛:1.应用基本不等式求最值时,经常要对所给式子进行变形,配凑,变形的目标是能配凑出“和”或“积”为定值的条件.2.若条件式是ax +by =c (a ,b ,c 都是正常数),常常进行常数代换(或乘除常数).如x +y =1(x >0,y >0)求1x+2y 的最值时,可以将1=x +y,2=2(x +y )代入,也可以变形1x +2y =(1x +2y )·1=(1x +2y)·(xy ).两种方法本质相同,若已知条件为2x +y =3(x >0,y >0),求3x +2y 的最值时,可利用3x +2y =13(3x +2y)(2x +y )变形. 3.求二元函数最值时,可以用代入消元法转化,但要注意根据被代换的变量的范围,对保留下的变量的范围加以限制.考点3、忽视等号成立的条件而致误例3.已知正数x 、y 满足x +2y =1,求1x +1y 的最小值.【答案】3+2 2【解析】[错解]由1=x +2y ≥22xy ,得1xy ≥22, ∴1x +1y ≥21xy =2xy ≥42,即1x +1y 的最小值为42. [辨析]两个等号不能同时取到,前一个不等式等号成立的条件是x =2y =12,后一个不等式等号则是当x =y 时成立.[正解]∵x 、y 为正数,且x +2y =1.∴1x +1y =(x +2y )(1x +1y )=3+2y x +x y ≥3+22,当且仅当2y x =x y ,即当x =2-1,y =1-22时等号成立. ∴1x +1y 的最小值为3+22.考点4、利用基本不等式比较数的大小例4.已知m =a +1a -2(a >2),n =22-b 2(b ≠0),则m 、n 之间的大小关系是 . 【答案】m >n 【解析】 ∵a >2,∴a -2>0.又∵m =a +1a -2=(a -2)+1a -2+2, ∴m ≥2a -2×1a -2+2=4,即m ∈[4,+∞). 由b ≠0,得b 2≠0,∴2-b 2<2,∴22-b 2<4,即n <4,∴n ∈(0,4).综上易得m >n .考点5、不等式的证明技巧—字母轮换不等式的证法例5.已知,,a b c 是全不相等的正实数,证明:3b c a a c b a b c a b c +-+-+-++>. 【答案】详见解析【解析】(方法一) ∵a,b,c 全不相等,∴,,b a c a c b a b a c b c 与与与全不相等 ∴b a a b +>2,c a a c +>2,c b b c+>2 三式相加得,b c c a a b a a b b c c+++++>6 ∴(1)(1)(1)b c c a a b a a b b c c+-++-++->3 即b c a a c b a b c a b c+-+-+-++>3 (方法二)要证b c a a c b a b c a b c+-+-+-++>3 只需证明111b c c a a b a a b b c c+-++-++->3 即证b c c a a b a a b b c c+++++>6 而事实上,由a,b,c 是全不相等的正实数,∴b a a b +>2,c a a c +>2,c b b c+>2 ∴b c c a a b a a b b c c+++++>6 ∴b c a a c b a b c a b c+-+-+-++>3得证考点点睛:证明不等式时,要注意观察分析其结构特征选取相应的证明方法.若不等式中字母具有轮换对称关系,则常常连用几个形式相同字母不同的不等式迭加获证.考点6、求参数的取值范围问题例6.【河南省开封市五县联考2019-2020学年高二上学期期末】已知0m >,0n >,141m n+=,若不等式22m n x x a +≥-++对已知的m ,n 及任意实数x 恒成立,则实数a 的取值范围是( ) A .[)8,+∞B .[)3,+∞C .(],3-∞D .(],8-∞ 【答案】D【解析】∵()1445n m m n m n m n m n ⎛⎫+=++=++⎪⎝⎭4529n m m n ≥+⨯=, 当且仅当4n m m n=时等号成立, ∴229x x a -++≤,即()222918a x x x ≤-+=-+,∴8a ≤.故选:D考点点睛:1.恒成立问题求参数的取值范围,常用“分离参数”转化为函数最值问题求解;2.解题思路来源于细致的观察,丰富的联想和充分的知识、技能的储备,要注意总结记忆.考点7、均值不等式在实际问题中的应用例7.如图,金砂公园有一块边长为2的等边ABC V 的边角地,现修成草坪,图中DE 把草坪分成面积相等的两部分,D 在AB 上,E 在AC 上.(Ⅰ)设AD x =,DE y =,求y 关于x 的函数关系式;(Ⅱ)如果DE 是灌溉水管,我们希望它最短,则DE 的位置应在哪里?请予以证明.【答案】(Ⅰ)2242(12)y x x x=+-≤≤;(Ⅱ)//DE BC ,且2DE =. 【解析】 (Ⅰ)在ADE V 中,222222cos60y x AE x AE x AE x AE =+-⋅⋅=+-⋅o ①, 又12ADE ABC S S =V V ,即11sin 6022sin 6024x AE ⋅⋅⋅=⋅⋅⋅o o ,即2AE x=②, 将②代入①,得222222422y x x x x ⎛⎫=+-=+- ⎪⎝⎭, 又2x ≤,若1x <,则22AE x=>不符合题意,所以1x ≥, 因此2242(12)y x x x =+-≤≤; (Ⅱ)如果DE 是水管, 因为2242422y x x =+-≥-=, 当且仅当224x x=,即2x =时“=”成立, 故//DE BC ,且2DE =.。
高中数学人教A版必修五3.4基本不等式(三)ppt课件

课后作业
1. 阅读教材P.97-P.100; 2.《习案》作业三十三.
3.4基本不等式:
ab ab 2
复习引入
基本不等式:
a2b2 2a b; ab a(b a0,b0).
2
讲授新课
例1. a,b是正 ab 数 4 , 且 a求 的 b 最 . 值
讲授新课
例1. a,b是正 ab 数 4 , 且 a求 的 b 最 . 值 变式1. a,b是正 2a 数 b4 , 且 a求 的 b 最 .
讲授新课
练习. (1)已a知 、 bR,且 a2b1,y11,
ab 求 y的 最 小 值 .
(2)已a、 知 b、 cR, 且 abc1, 求:证 1119.
abc (3)已a、 知 b、 cR, 且 abc1, 求:证 (11)1 (1)1 (1)8.
abc
课堂小结
1.熟练使用 a2b不 22a等 和 ba式 b2a. b 2.注意使 ab用 2 a的 b 条件. 3. 注意取等号的条件.
讲授新课
例1. a,b是正 ab 数 4 , 且 a求 的 b 最 . 值 变式1. a,b是正 2a 数 b4 , 且 a求 的 b 最 . 变式2. a,b是 正a数 b4, 且a求 的 b 最 .
2
讲授新课
例1. a,b是正 ab 数 4 , 且 a求 的 b 最 . 值
变式1. a,b是正 2a 数 b4 , 且 a求 的 b 最 . 变式2. a,b是 正a数 b4, 且a求 的 b 最 .
2
变式3. a,b是正数且2a+3b=4,求ab的最值和 此时a、b的值.
讲授新课
例2. (1)a,b都是正数且2a+b=2,求a(1+b)
新课标人教A版高中数学必修五典题精讲(3.4基本不等式)

新课标人教A 版高中数学必修五典题精讲(3.4基本不等式)典题精讲例1(1)已知0<x <31,求函数y=x(1-3x)的最大值; (2)求函数y=x+x1的值域. 思路分析:(1)由极值定理,可知需构造某个和为定值,可考虑把括号内外x 的系数变成互为相反数;(2)中,未指出x >0,因而不能直接使用基本不等式,需分x >0与x <0讨论. (1)解法一:∵0<x <31,∴1-3x >0. ∴y=x(1-3x)= 31·3x(1-3x)≤31[2)31(3x x -+]2=121,当且仅当3x=1-3x ,即x=61时,等号成立.∴x=61时,函数取得最大值121. 解法二:∵0<x <31,∴31-x >0. ∴y=x(1-3x)=3x(31-x)≤3[231x x -+]2=121,当且仅当x=31-x,即x=61时,等号成立. ∴x=61时,函数取得最大值121. (2)解:当x >0时,由基本不等式,得y=x+x 1≥2xx 1∙=2,当且仅当x=1时,等号成立. 当x <0时,y=x+x 1=-[(-x)+)(1x -]. ∵-x >0,∴(-x)+)(1x -≥2,当且仅当-x=x -1,即x=-1时,等号成立. ∴y=x+x1≤-2. 综上,可知函数y=x+x 1的值域为(-∞,-2]∪[2,+∞). 绿色通道:利用基本不等式求积的最大值,关键是构造和为定值,为使基本不等式成立创造条件,同时要注意等号成立的条件是否具备.变式训练1当x >-1时,求f(x)=x+11+x 的最小值. 思路分析:x >-1⇒x+1>0,变x=x+1-1时x+1与11+x 的积为常数. 解:∵x >-1,∴x+1>0.∴f(x)=x+11+x =x+1+11+x -1≥2)1(1)1(+∙+x x -1=1. 当且仅当x+1=11+x ,即x=0时,取得等号.∴f(x)min =1.变式训练2求函数y=133224+++x x x 的最小值. 思路分析:从函数解析式的结构来看,它与基本不等式结构相差太大,而且利用前面求最值的方法不易求解,事实上,我们可以把分母视作一个整体,用它来表示分子,原式即可展开.解:令t=x 2+1,则t≥1且x 2=t-1.∴y=133224+++x x x =1113)1(3)1(22++=++=+-+-t t t t t t t t . ∵t≥1,∴t+t 1≥2tt 1∙=2,当且仅当t=t 1,即t=1时,等号成立. ∴当x=0时,函数取得最小值3.例2已知x >0,y >0,且x 1+y9=1,求x+y 的最小值. 思路分析:要求x+y 的最小值,根据极值定理,应构建某个积为定值,这需要对条件进行必要的变形,下面给出三种解法,请仔细体会.解法一:利用“1的代换”,∵x 1+y9=1, ∴x+y=(x+y)·(x 1+y 9)=10+yx x y 9+. ∵x >0,y >0,∴y x x y 9+≥2yx x y 9∙=6. 当且仅当yx x y 9=,即y=3x 时,取等号. 又x 1+y9=1,∴x=4,y=12. ∴当x=4,y=12时,x+y 取得最小值16.解法二:由x 1+y 9=1,得x=9-y y . ∵x >0,y >0,∴y >9. x+y=9-y y +y=y+999-+-y y =y+99-y +1=(y-9)+99-y +10. ∵y >9,∴y-9>0.∴999-+-y y ≥299)9(-∙-y y =6. 当且仅当y-9=99-y ,即y=12时,取得等号,此时x=4.∴当x=4,y=12时,x+y 取得最小值16.解法三:由x 1+y 9=1,得y+9x=xy,∴(x-1)(y-9)=9.∴x+y=10+(x-1)+(y-9)≥10+2)9)(1(--y x =16,当且仅当x-1=y-9时取得等号.又x 1+y9=1, ∴x=4,y=12.∴当x=4,y=12时,x+y 取得最小值16.绿色通道:本题给出了三种解法,都用到了基本不等式,且都对式子进行了变形,配凑出基本不等式满足的条件,这是经常需要使用的方法,要学会观察,学会变形,另外解法二,通过消元,化二元问题为一元问题,要注意根据被代换的变量的范围对另外一个变量的范围的影响.黑色陷阱:本题容易犯这样的错误:x 1+y 9≥2xy 9①,即xy6≤1,∴xy ≥6. ∴x+y≥2xy ≥2×6=12②.∴x+y 的最小值是12.产生不同结果的原因是不等式①等号成立的条件是x 1=y9,不等式②等号成立的条件是x=y.在同一个题目中连续运用了两次基本不等式,但是两个基本不等式等号成立的条件不同,会导致错误结论.变式训练已知正数a,b,x,y 满足a+b=10,y b x a +=1,x+y 的最小值为18,求a,b 的值. 思路分析:本题属于“1”的代换问题.解:x+y=(x+y)(y b x a +)=a+x ay y bx ++b=10+xay y bx +. ∵x,y >0,a,b >0,∴x+y≥10+2ab =18,即ab =4.又a+b=10,∴⎩⎨⎧==8,2b a 或⎩⎨⎧==.2,8b a 例3求f(x)=3+lgx+xlg 4的最小值(0<x <1). 思路分析:∵0<x <1,∴lgx <0,xlg 4<0不满足各项必须是正数这一条件,不能直接应用基本不等式,正确的处理方法是加上负号变正数. 解:∵0<x <1,∴lgx <0,x lg 4<0.∴-x lg 4>0. ∴(-lgx)+(-x lg 4)≥2)lg 4)(lg (xx --=4. ∴lgx+x lg 4≤-4.∴f(x)=3+lgx+xlg 4≤3-4=-1. 当且仅当lgx=x lg 4,即x=1001时取得等号. 则有f(x)=3+lgx+xlg 4 (0<x <1)的最小值为-1. 黑色陷阱:本题容易忽略0<x <1这一个条件.变式训练1已知x <45,求函数y=4x-2+541-x 的最大值. 思路分析:求和的最值,应凑积为定值.要注意条件x <45,则4x-5<0. 解:∵x <45,∴4x-5<0. y=4x-5+541-x +3=-[(5-4x)+x 451-]+3 ≤-2x x 451)45(-∙-+3=-2+3=1. 当且仅当5-4x=x 451-,即x=1时等号成立. 所以当x=1时,函数的最大值是1. 变式训练2当x <23时,求函数y=x+328-x 的最大值. 思路分析:本题是求两个式子和的最大值,但是x·328-x 并不是定值,也不能保证是正值,所以,必须使用一些技巧对原式变形.可以变为y=21(2x-3)+328-x +23=-(xx 238223-+-)+23,再求最值. 解:y=21(2x-3)+328-x +23=-(xx 238223-+-)+23, ∵当x <23时,3-2x >0, ∴x x 238223-+-≥xx 2382232-∙-=4,当且仅当x x 238223-=-,即x=-21时取等号.于是y≤-4+23=25-,故函数有最大值25-. 例4如图3-4-1,动物园要围成相同的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.图3-4-1(1)现有可围36 m 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?(2)若使每间虎笼面积为24 m 2,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋总长度最小?思路分析:设每间虎笼长为x m ,宽为y m ,则(1)是在4x+6y=36的前提下求xy 的最大值;而(2)则是在xy=24的前提下来求4x+6y 的最小值.解:(1)设每间虎笼长为x m ,宽为y m ,则由条件,知4x+6y=36,即2x+3y=18.设每间虎笼的面积为S ,则S=xy.方法一:由于2x+3y≥2y x 32⨯=2xy 6,∴2xy 6≤18,得xy≤227,即S≤227. 当且仅当2x=3y 时等号成立.由⎩⎨⎧=+=,1832,22y x y x 解得⎩⎨⎧==.3,5.4y x 故每间虎笼长为4.5 m ,宽为3 m 时,可使面积最大.方法二:由2x+3y=18,得x=9-23y. ∵x >0,∴0<y <6.S=xy=(9-23y)y=23 (6-y)y. ∵0<y <6,∴6-y >0.∴S≤23[2)6(y y +-]2=227. 当且仅当6-y=y,即y=3时,等号成立,此时x=4.5.故每间虎笼长4.5 m,宽3 m 时,可使面积最大.(2)由条件知S=xy=24.设钢筋网总长为l,则l=4x+6y.方法一:∵2x+3y≥2y x 32∙=2xy 6=24,∴l=4x+6y=2(2x+3y)≥48,当且仅当2x=3y 时,等号成立.由⎩⎨⎧==,24,32xy y x 解得⎩⎨⎧==.4,6y x 故每间虎笼长6 m ,宽4 m 时,可使钢筋网总长最小. 方法二:由xy=24,得x=y 24. ∴l=4x+6y=y 96+6y=6(y 16+y)≥6×2y y⨯16=48,当且仅当y 16=y ,即y=4时,等号成立,此时x=6.故每间虎笼长6 m,宽4 m 时,可使钢筋总长最小.绿色通道:在使用基本不等式求函数的最大值或最小值时,要注意:(1)x,y 都是正数;(2)积xy (或x+y )为定值;(3)x 与y 必须能够相等,特别情况下,还要根据条件构造满足上述三个条件的结论.变式训练某工厂拟建一座平面图为矩形且面积为200 平方米的三级污水处理池(平面图如图3-4-2所示),由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两道隔墙建造单价为每米248元,池底建造单价为每平方米80元,池壁的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求出最低造价.图3-4-2思路分析:在利用均值不等式求最值时,必须考虑等号成立的条件,若等号不能成立,通常要用函数的单调性进行求解.解:设污水处理池的长为x 米,则宽为x 200米(0<x≤16,0<x200≤16),∴12.5≤x≤16. 于是总造价Q(x)=400(2x+2×x 200)+248×2×x 200+80×200. =800(x+x 324)+16 000≥800×2xx 324∙+16 000=44 800, 当且仅当x=x 324 (x >0),即x=18时等号成立,而18∉[12.5,16],∴Q(x)>44 800. 下面研究Q(x)在[12.5,16]上的单调性.对任意12.5≤x 1<x 2≤16,则x 2-x 1>0,x 1x 2<162<324.Q(x 2)-Q(x 1)=800[(x 2-x 1)+324(1211x x -)] =800×212112)324)((x x x x x x --<0, ∴Q(x 2)>Q(x 1).∴Q(x)在[12.5,16]上是减函数.∴Q(x)≥Q(16)=45 000.答:当污水处理池的长为16米,宽为12.5米时,总造价最低,最低造价为45 000元.问题探究问题某人要买房,随着楼层的升高,上下楼耗费的精力增多,因此不满意度升高.当住第n 层楼时,上下楼造成的不满意度为n.但高处空气清新,嘈杂音较小,环境较为安静,因此随着楼层的升高,环境不满意度降低.设住第n 层楼时,环境不满意程度为n8.则此人应选第几楼,会有一个最佳满意度. 导思:本问题实际是求n 为何值时,不满意度最小的问题,先要根据问题列出一个关于楼层的函数式,再根据基本不等式求解即可.探究:设此人应选第n 层楼,此时的不满意程度为y.由题意知y=n+n8.∵n+n 8≥2248=⨯nn , 当且仅当n=n 8,即n=22时取等号. 但考虑到n ∈N *,∴n≈2×1.414=2.828≈3,即此人应选3楼,不满意度最低.选校网高考频道专业大全历年分数线上万张大学图片大学视频院校库(按ctrl 点击打开)选校网()是为高三同学和家长提供高考选校信息的一个网站。
高中数学人教A版必修5不等式基本不等式名师课件PPT
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
新西知工探究大 附 中
作差法 能
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
西
工
大
附
中
01
重要不等式
把已有的知识进行变形,是我们 数学研究中推陈出新的重要方法
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
典例分析
例1.判断对错.
为正
等号成立条件
× ×
定值 √ √
注意:一正二定三相等
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
数形结合 数学建模 逻辑推理
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
西
工
大
附
中
基本不等式其实是柯西 不等式的一种特例,它在 高中数学中扮演着重要 的角色,请同学们利用课 余时间查阅互联网和相 关文献,为后面学习基本 不等式的应用做好准备.
作业
课本P100 1、练习2 2、习题3.4
A组 第2、3题
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】 高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
高中数学【人教A版必修】5不等式基 本不等 式名师 课件PPT 【完美 课件】
高中数学人教版必修五:基本不等式(共23张PPT)
ab
a
b 2
(第一课时)
2019/10/5
一、情境创设 导入课题
第24届国际数学家大会(ICM2002)的会标
问题 :你能在这个图中找出一些相等关系或不 等关系吗?
二、自主探究 推导公式
问题 1:在正方形 ABCD 中有4个全等的直角三角形.设直角三角形的
两条直角边长为a,b,正方形ABCD的面积为 S ,4个直角三角形的面积和
2
又称为基本不等式
4、从数列角度看:
把
ab 2
看做两个正数a,b 的等差中项,
ab 看做正数a,b的等比中项,
那么上面不等式可以叙述为:
两个正数的等差中项不小于它们的等比 中项。
还有没有其它的证明方法证明均值 不等式呢?
二、自主探究 推导公式 探究:如图,AB 是圆的直径,点 C 是 AB上一点,
显然,④是成立的.当且仅当 a b 时,④中的等号成立.
2019/10/5
析 : a 0,b 0,
a b ab a b 2 ab ( a b)2 0
2
2
2
即 a b ab 2
当且仅当 a b即a b等号成立
上面所证结论通常称为均值不等式
(2)设矩形的长、宽分别为x(m),y(m),
依题意有2(x+y)=36,即x+y=18, 因为x>0,y>0,所以, xy ≤ x y
2
因此 xy ≤9
将这个正值不等式的两边平方,得xy≤81, 当且仅当x=y时,式中等号成立,此时x=y=9,
因此,当这个矩形的长与宽都是9m时,它的 面积最大,最大值是81m2。
高中数学必修五教案-3.4 基本不等式(11)-人教A版
3.42a b+≤基本不等式的应用是对有关基本不等式知识的巩固与提高。
其中重点讲解了“和定积最大”、“积定和最小”两个定理(命题)在解决数学最值问题方面的作用,通过例题和练习,让学生掌握这两个定理(命题)成立的前提条件:“一正二定三相等”,从而进一步运用它们解决一些与最值有关的数学问题与实际问题. 【教学目标】:知识与技能: 使学生掌握“和定积最大”、“积定和最小”两个定理(命题)在解决数学最值问题方面的应用过程与方法: 通过例题和练习,让学生掌握这两个定理(命题)成立的前提条件:“一正二定三相等”情态与价值:使学生准确掌握这两个定理(命题)及其成立的前提条件,并会运用它们解决一些与最值有关的数学问题与实际问题 【教学重点】:“和定积最大”、“积定和最小”两个定理(命题)在解决数学最值问题方面的应用;【教学难点】:两个定理(命题)成立的前提条件:“一正二定三相等” 【教学方法】:探究启发式分层次教学【教学突破点】:从例题出发,强调两个定理(命题)成立的前提条件:“一正二定三相等”的重要性及应用过程中的注意事项。
【教学过程设计】:1.若a 、b 是正数,则2b a +、ab 、ba ab+2、222b a +这四个数的大小顺序是A.ab ≤2b a +≤ba ab+2≤222b a +B.222b a +≤ab ≤2b a +≤b a ab +2C.b a ab +2≤ab ≤2ba +≤222b a +D.ab ≤2b a +≤222b a +≤ba ab+2解析:可设a =1,b =2, 则2b a +=23,ab =2, b a ab +2=34, 222b a +=241+=25=5.2. 答案:C2. 设42,=+∈+y x R y x 且,则y x lg lg +的最大值是( )A .2lg -B .2lgC .2lg 2D .2解析:设42,=+∈+y x R y x 且,则2222=+≤⋅yx y x ,即2≤xy 故y x lg lg +=2lg )lg(≤xy 答案 :B3. 设1(,=+-∈+)且y x xy R y x ,则x +y 的最小值为_________ 解析:∵2)2(y x xy +≤∴1)(4)(2≥+-+y x y x , x +y ≥222+ 答案: 222+4.设x >0,y >0,且xy -(x +y )=1,则A.x +y ≤22+2B.x +y ≥22+2C.x +y ≤(2+1)2D.x +y ≥(2+1)2解析:∵x >0,y >0,∴xy ≤(2y x +)2. 由xy -(x +y )=1得(2y x +)2-(x +y )≥1. ∴x +y ≥2+22.答案:B5.如果0<a <1,0<x ≤y <1,且log a x log a y =1,那么xyA.无最大值也无最小值B.有最大值无最小值C.无最大值有最小值D.有最大值也有最小值解析:∵log a x +log a y ≥2y x a a log log =2, ∴log a xy ≥2. ∴0<xy ≤a 2. 答案:B6.已知正数x 、y 满足x +2y =1,求x 1+y1的最小值. 解析:∵x 、y 为正数,且x +2y =1,∴x 1+y 1=(x +2y )(x 1+y 1) =3+x y 2+yx≥3+22, 当且仅当x y 2=yx,即当x =2-1,y =1-22时等号成立.∴x 1+y1的最小值为3+22. 答案:x 1+y 1的最小值为3+22.7.设M =a +21-a (2<a <3),N =log 21(x 2+161)(x ∈R ),那么M 、N 的大小关系是A.M >NB.M =NC.M <ND.不能确定解析:由2<a <3,M =a +21-a =(a -2)+21-a +2>2+2=4(注意a ≠1,a ≠3), N =log 21(x 2+161)≤log 21161=4<M . 答案:A。
《基本不等式》典型例题
高中数学必修五典题精讲典题精讲例1(1)已知0<x <31,求函数y=x(1-3x)的最大值; (2)求函数y=x+x1的值域. 思路分析:(1)由极值定理,可知需构造某个和为定值,可考虑把括号内外x 的系数变成互为相反数;(2)中,未指出x >0,因而不能直接使用基本不等式,需分x >0与x <0讨论.(1)解法一:∵0<x <31,∴1-3x >0. ∴y=x(1-3x)= 31·3x(1-3x)≤31[2)31(3x x -+]2=121,当且仅当3x=1-3x ,即x=61时,等号成立.∴x=61时,函数取得最大值121. 解法二:∵0<x <31,∴31-x >0. ∴y=x(1-3x)=3x(31-x)≤3[231x x -+]2=121,当且仅当x=31-x,即x=61时,等号成立. ∴x=61时,函数取得最大值121. (2)解:当x >0时,由基本不等式,得y=x+x1≥2x x 1•=2,当且仅当x=1时,等号成立. 当x <0时,y=x+x1=-[(-x)+)(1x -]. ∵-x >0,∴(-x)+)(1x -≥2,当且仅当-x=x -1,即x=-1时,等号成立. ∴y=x+x1≤-2. 综上,可知函数y=x+x 1的值域为(-∞,-2]∪[2,+∞). 绿色通道:利用基本不等式求积的最大值,关键是构造和为定值,为使基本不等式成立创造条件,同时要注意等号成立的条件是否具备.变式训练1当x >-1时,求f(x)=x+11+x 的最小值. 思路分析:x >-1⇒x+1>0,变x=x+1-1时x+1与11+x 的积为常数. 解:∵x >-1,∴x+1>0.∴f(x)=x+11+x =x+1+11+x -1≥2)1(1)1(+•+x x -1=1. 当且仅当x+1=11+x ,即x=0时,取得等号. ∴f(x)min =1.变式训练2求函数y=133224+++x x x 的最小值. 思路分析:从函数解析式的结构来看,它与基本不等式结构相差太大,而且利用前面求最值的方法不易求解,事实上,我们可以把分母视作一个整体,用它来表示分子,原式即可展开.解:令t=x 2+1,则t ≥1且x 2=t-1.∴y=133224+++x x x =1113)1(3)1(22++=++=+-+-t t t t t t t t . ∵t ≥1,∴t+t 1≥2t t 1•=2,当且仅当t=t1,即t=1时,等号成立. ∴当x=0时,函数取得最小值3.例2已知x >0,y >0,且x 1+y9=1,求x+y 的最小值. 思路分析:要求x+y 的最小值,根据极值定理,应构建某个积为定值,这需要对条件进行必要的变形,下面给出三种解法,请仔细体会.解法一:利用“1的代换”, ∵x 1+y9=1, ∴x+y=(x+y)·(x 1+y9)=10+y x x y 9+. ∵x >0,y >0,∴y x x y 9+≥2y x x y 9•=6. 当且仅当yx x y 9=,即y=3x 时,取等号. 又x 1+y9=1,∴x=4,y=12. ∴当x=4,y=12时,x+y 取得最小值16.解法二:由x 1+y9=1,得x=9-y y . ∵x >0,y >0,∴y >9. x+y=9-y y +y=y+999-+-y y =y+99-y +1=(y-9)+99-y +10. ∵y >9,∴y-9>0. ∴999-+-y y ≥299)9(-•-y y =6. 当且仅当y-9=99-y ,即y=12时,取得等号,此时x=4.∴当x=4,y=12时,x+y 取得最小值16.解法三:由x 1+y9=1,得y+9x=xy, ∴(x-1)(y-9)=9.∴x+y=10+(x-1)+(y-9)≥10+2)9)(1(--y x =16,当且仅当x-1=y-9时取得等号.又x 1+y9=1, ∴x=4,y=12.∴当x=4,y=12时,x+y 取得最小值16.绿色通道:本题给出了三种解法,都用到了基本不等式,且都对式子进行了变形,配凑出基本不等式满足的条件,这是经常需要使用的方法,要学会观察,学会变形,另外解法二,通过消元,化二元问题为一元问题,要注意根据被代换的变量的范围对另外一个变量的范围的影响.黑色陷阱:本题容易犯这样的错误:x 1+y 9≥2xy 9①,即xy6≤1,∴xy ≥6. ∴x+y ≥2xy ≥2×6=12②.∴x+y 的最小值是12.产生不同结果的原因是不等式①等号成立的条件是x 1=y9,不等式②等号成立的条件是x=y.在同一个题目中连续运用了两次基本不等式,但是两个基本不等式等号成立的条件不同,会导致错误结论.变式训练已知正数a,b,x,y 满足a+b=10,y b x a +=1,x+y 的最小值为18,求a,b 的值. 思路分析:本题属于“1”的代换问题.解:x+y=(x+y)(y b x a +)=a+x ay y bx ++b=10+xay y bx +. ∵x,y >0,a,b >0,∴x+y ≥10+2ab =18,即ab =4.又a+b=10,∴⎩⎨⎧==8,2b a 或⎩⎨⎧==.2,8b a例3求f(x)=3+lgx+x lg 4的最小值(0<x <1). 思路分析:∵0<x <1,∴lgx <0,xlg 4<0不满足各项必须是正数这一条件,不能直接应用基本不等式,正确的处理方法是加上负号变正数.解:∵0<x <1,∴lgx <0,x lg 4<0.∴-xlg 4>0. ∴(-lgx)+(-x lg 4)≥2)lg 4)(lg (xx --=4. ∴lgx+x lg 4≤-4.∴f(x)=3+lgx+xlg 4≤3-4=-1. 当且仅当lgx=x lg 4,即x=1001时取得等号. 则有f(x)=3+lgx+x lg 4 (0<x <1)的最小值为-1. 黑色陷阱:本题容易忽略0<x <1这一个条件.变式训练1已知x <45,求函数y=4x-2+541-x 的最大值.思路分析:求和的最值,应凑积为定值.要注意条件x <45,则4x-5<0. 解:∵x <45,∴4x-5<0. y=4x-5+541-x +3=-[(5-4x)+x 451-]+3 ≤-2xx 451)45(-•-+3=-2+3=1. 当且仅当5-4x=x451-,即x=1时等号成立. 所以当x=1时,函数的最大值是1.变式训练2当x <23时,求函数y=x+328-x 的最大值. 思路分析:本题是求两个式子和的最大值,但是x ·328-x 并不是定值,也不能保证是正值,所以,必须使用一些技巧对原式变形.可以变为y=21(2x-3)+328-x +23=-(x x 238223-+-)+23,再求最值.解:y=21(2x-3)+328-x +23=-(x x 238223-+-)+23, ∵当x <23时,3-2x >0, ∴x x 238223-+-≥x x 2382232-•-=4,当且仅当x x 238223-=-,即x=-21时取等号. 于是y ≤-4+23=25-,故函数有最大值25-. 例4如图3-4-1,动物园要围成相同的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.图3-4-1(1)现有可围36 m 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?(2)若使每间虎笼面积为24 m 2,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋总长度最小?思路分析:设每间虎笼长为x m ,宽为y m ,则(1)是在4x+6y=36的前提下求xy 的最大值;而(2)则是在xy=24的前提下来求4x+6y 的最小值.解:(1)设每间虎笼长为x m ,宽为y m ,则由条件,知4x+6y=36,即2x+3y=18.设每间虎笼的面积为S ,则S=xy.方法一:由于2x+3y ≥2y x 32⨯=2xy 6,∴2xy 6≤18,得xy ≤227,即S ≤227. 当且仅当2x=3y 时等号成立.由⎩⎨⎧=+=,1832,22y x y x 解得⎩⎨⎧==.3,5.4y x故每间虎笼长为4.5 m ,宽为3 m 时,可使面积最大. 方法二:由2x+3y=18,得x=9-23y. ∵x >0,∴0<y <6. S=xy=(9-23y)y=23 (6-y)y. ∵0<y <6,∴6-y >0.∴S ≤23[2)6(y y +-]2=227. 当且仅当6-y=y,即y=3时,等号成立,此时x=4.5.故每间虎笼长4.5 m,宽3 m 时,可使面积最大.(2)由条件知S=xy=24.设钢筋网总长为l,则l=4x+6y.方法一:∵2x+3y ≥2y x 32•=2xy 6=24,∴l=4x+6y=2(2x+3y)≥48,当且仅当2x=3y 时,等号成立.由⎩⎨⎧==,24,32xy y x 解得⎩⎨⎧==.4,6y x故每间虎笼长6 m ,宽4 m 时,可使钢筋网总长最小. 方法二:由xy=24,得x=y 24. ∴l=4x+6y=y 96+6y=6(y 16+y)≥6×2y y⨯16=48,当且仅当y 16=y ,即y=4时,等号成立,此时x=6. 故每间虎笼长6 m,宽4 m 时,可使钢筋总长最小.绿色通道:在使用基本不等式求函数的最大值或最小值时,要注意:(1)x,y 都是正数;(2)积xy (或x+y )为定值;(3)x 与y 必须能够相等,特别情况下,还要根据条件构造满足上述三个条件的结论.变式训练某工厂拟建一座平面图为矩形且面积为200 平方米的三级污水处理池(平面图如图3-4-2所示),由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两道隔墙建造单价为每米248元,池底建造单价为每平方米80元,池壁的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求出最低造价.图3-4-2思路分析:在利用均值不等式求最值时,必须考虑等号成立的条件,若等号不能成立,通常要用函数的单调性进行求解.解:设污水处理池的长为x 米,则宽为x 200米(0<x ≤16,0<x200≤16),∴12.5≤x ≤16. 于是总造价Q(x)=400(2x+2×x 200)+248×2×x 200+80×200. =800(x+x324)+16 000≥800×2x x 324•+16 000=44 800, 当且仅当x=x324 (x >0),即x=18时等号成立,而18∉[12.5,16],∴Q(x)>44 800. 下面研究Q(x)在[12.5,16]上的单调性.对任意12.5≤x 1<x 2≤16,则x 2-x 1>0,x 1x 2<162<324.Q(x 2)-Q(x 1)=800[(x 2-x 1)+324(1211x x -)] =800×212112)324)((x x x x x x --<0, ∴Q(x 2)>Q(x 1).∴Q(x)在[12.5,16]上是减函数.∴Q(x)≥Q(16)=45 000.答:当污水处理池的长为16米,宽为12.5米时,总造价最低,最低造价为45 000元.问题探究问题某人要买房,随着楼层的升高,上下楼耗费的精力增多,因此不满意度升高.当住第n 层楼时,上下楼造成的不满意度为n.但高处空气清新,嘈杂音较小,环境较为安静,因此随着楼层的升高,环境不满意度降低.设住第n 层楼时,环境不满意程度为n8.则此人应选第几楼,会有一个最佳满意度.导思:本问题实际是求n 为何值时,不满意度最小的问题,先要根据问题列出一个关于楼层的函数式,再根据基本不等式求解即可.探究:设此人应选第n 层楼,此时的不满意程度为y.由题意知y=n+n8.∵n+n8≥2248=⨯n n , 当且仅当n=n8,即n=22时取等号. 但考虑到n ∈N *,∴n ≈2×1.414=2.828≈3,即此人应选3楼,不满意度最低.。
人教高中数学A版必修5 基本不等式 精讲精析
3·4 基本不等式1.若a,b ∈R ,则a 2+b 2≥2ab ,当且仅当a=b 时取等号.2.设a,b ∈R+,则称2b a +为a,b 的算术平均值;称ab 为a,b 的几何平均值.3.平均值不等式的原形与变形①2b a +≥ab (当且仅当a=b 时取等号)为原形. ②变形有:a+b ≥ab 2;ab ≤22⎪⎭⎫ ⎝⎛+b a ,当且仅当a=b 时取等号. 4.利用平均值不等式求最大最小值,是对“能取等号”而言的.要注意不能取等号的情况.5.最值定理如果a,b ∈R+,a·b=P (定值),当且仅当a=b 时,a+b 有最小值P 2;如果a,b ∈R+,且a+b=S (定值),当且仅当a=b 时,ab 有最大值42S .【例1】 设x ∈[2,5),求下列函数的最值.(1)y =(3+2x )·(6-x );(2)y =(3+2x )·(4-x );(3)y =4x -9·2x +1+80;(4)y =6722++x x . 分析 (1)因3+2x =12-2x 时,x =49∈[2,5],故可直接应用平均值不等式; (2)因3+2x =8-2x 时,x =45但45∉[2,5]故不能使用平均值不等式; (3)可分解为y =(2x -8)·(2x -10);(4)因方程61622+=+x x 无根,故不能使用平均值不等式,而考虑其“单调性”.解 (1)y =(3+2x )·(6-x )=21·(3+2x )·(12-2x ) ≤21×41[(3+2x )+(12-2x )]2=8225 ,当且仅当3+2x =12-2x ,即x =49时,y m ax =8225 ,又∵x =2时,y =28;x =5时,y =13<28,故函数只有最大值8225 ,而没有最小值. (2)因y =(3+2x )·(4-x )=-2x 2+5x +12,其对称轴为x =45,故函数在[2,5)上单调减;当x =2时,y m ax =(3+4)·(4-2)=14,函数没有最小值.(3)分解因式得:y =(2x -8)·(2x -10)=-(2x -8)·(10-2x )≥-22810⎪⎭⎫ ⎝⎛-=-1,故y min =-1,又当x =2时,y =(4-8)·(4-10)=24,当x =5时,y =(32-8)·(32-10)=528.故当且仅当x =2时,函数有最小值-1,而函数没有最大值(x =5∉[2,5]].(4)易证函数在[2,5]上单调增,故当x =2时,y min =101011,又因5∉[2,5],故函数没有最大值. 说明 利用平均值不等式求最值时,应考虑诸项条件是否齐备,对两个正数而言:和定→相等时→积最大;积定→相等时→和最小.在求函数的最值时,若不能使用平均值不等式,则可以考察函数的单调性.【例2】 一开发商在某处想圈一块周长为L 的地皮,这块地皮既可以为长方形,也可以为圆形,欲使其面积最大,应确定为何种图形?何种尺寸?分析 设长方形的一边之长为x ,则邻边之长为2L -x ,则可先确定x ·(2L -x )的最大值. 解 若确定为圆形,则面积为π⎪⎭⎫ ⎝⎛π2L 2=π42L ;若确定为长方形,则不妨设其面积为S ,一边之长为x ,则邻边之长为2L -x ,故S =x ·(2L -x )≤161L 2. 当且仅当x =2L -x 即x =4L 时取等号. ∵41πL 2-161L 2=L 2⎪⎭⎫ ⎝⎛-16141π>0,∴应确定为圆形地皮.说明 在一切封闭平面图形中,若周长一定,则只有圆的面积最大.【例3】 若正数a 、b 满足ab ≥a+b +3,试求a+b 的取值范围.分析 设a+b=x ,利用平均值不等式,可推导出一个关于x 的不等式.解 设a+b=x ,则x >0,ab ≥x +3,又ab ≤22⎪⎭⎫ ⎝⎛+b a =42x ,故由不等式的传递性得42x ≥x +3,解之x ≥6,故a+b 的取值范围是[6,+∞]. 说明 求某表达式的取值范围,常可使用“换元法”,从而达到等价转化的目的.【例4】 已知:x 、y 、z ∈R+,且满足x+y+z =1,求zy x 941++的取值范围. 分析 不具备用平均值不等式的条件,但是x1+mx ,mz z my y ++9,4(m >0),则可用等价变形,构造使用平均值不等式的条件可求范围. 解 ∵x+y+z =1,引入参数m >0,∴mx+my+mz=m zy x 941++⇒ =(x1+mx )+( )9()4mz z my y +++-m ≥2m +4m +6m -m =12m -m . 当且仅当x 1=mx 且y 4=my 且z 9=mz ,即x =,1m 且y =m 2且z =m3时取等号. 代入x+y+z =1得: m 1+m 2+m 3=1.解之m =36.∴12m -m =1236-36=36.综上所述可知:zy x 941++的取值范围是[36,+∞). 说明 为了使用平均值不等式,可引入一个参数,构造一个含有参数的不等式,它能运用平均值不等式,使运算能进行下去,最后,依据相等的条件,可解出参数的值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教A版数学2016届复习资料姓名:沈金鹏院、系:数学学院专业: 数学与应用数学2015年12月10日新课标人教A 版高中数学必修五典题精讲(3.4基本不等式)典题精讲例1(1)已知0<x <31,求函数y=x(1-3x)的最大值; (2)求函数y=x+x1的值域. 思路分析:(1)由极值定理,可知需构造某个和为定值,可考虑把括号内外x 的系数变成互为相反数;(2)中,未指出x >0,因而不能直接使用基本不等式,需分x >0与x <0讨论.(1)解法一:∵0<x <31,∴1-3x >0. ∴y=x(1-3x)= 31·3x(1-3x)≤31[2)31(3x x -+]2=121,当且仅当3x=1-3x ,即x=61时,等号成立.∴x=61时,函数取得最大值121. 解法二:∵0<x <31,∴31-x >0. ∴y=x(1-3x)=3x(31-x)≤3[231x x -+]2=121,当且仅当x=31-x,即x=61时,等号成立. ∴x=61时,函数取得最大值121. (2)解:当x >0时,由基本不等式,得y=x+x 1≥2xx 1∙=2,当且仅当x=1时,等号成立. 当x <0时,y=x+x 1=-[(-x)+)(1x -]. ∵-x >0,∴(-x)+)(1x -≥2,当且仅当-x=x -1,即x=-1时,等号成立. ∴y=x+x1≤-2. 综上,可知函数y=x+x 1的值域为(-∞,-2]∪[2,+∞). 绿色通道:利用基本不等式求积的最大值,关键是构造和为定值,为使基本不等式成立创造条件,同时要注意等号成立的条件是否具备.变式训练1当x >-1时,求f(x)=x+11+x 的最小值.思路分析:x >-1⇒x+1>0,变x=x+1-1时x+1与11+x 的积为常数. 解:∵x >-1,∴x+1>0.∴f(x)=x+11+x =x+1+11+x -1≥2)1(1)1(+∙+x x -1=1. 当且仅当x+1=11+x ,即x=0时,取得等号. ∴f(x)min =1.变式训练2求函数y=133224+++x x x 的最小值. 思路分析:从函数解析式的结构来看,它与基本不等式结构相差太大,而且利用前面求最值的方法不易求解,事实上,我们可以把分母视作一个整体,用它来表示分子,原式即可展开. 解:令t=x 2+1,则t≥1且x 2=t-1.∴y=133224+++x x x =1113)1(3)1(22++=++=+-+-t t t t t t t t . ∵t≥1,∴t+t 1≥2tt 1∙=2,当且仅当t=t 1,即t=1时,等号成立. ∴当x=0时,函数取得最小值3.例2已知x >0,y >0,且x 1+y9=1,求x+y 的最小值. 思路分析:要求x+y 的最小值,根据极值定理,应构建某个积为定值,这需要对条件进行必要的变形,下面给出三种解法,请仔细体会.解法一:利用“1的代换”, ∵x 1+y9=1, ∴x+y=(x+y)·(x 1+y 9)=10+y x x y 9+. ∵x >0,y >0,∴y x x y 9+≥2yx x y 9∙=6. 当且仅当yx x y 9=,即y=3x 时,取等号.又x 1+y9=1,∴x=4,y=12. ∴当x=4,y=12时,x+y 取得最小值16. 解法二:由x 1+y 9=1,得x=9-y y . ∵x >0,y >0,∴y >9. x+y=9-y y +y=y+999-+-y y =y+99-y +1=(y-9)+99-y +10. ∵y >9,∴y-9>0. ∴999-+-y y ≥299)9(-∙-y y =6. 当且仅当y-9=99-y ,即y=12时,取得等号,此时x=4.∴当x=4,y=12时,x+y 取得最小值16.解法三:由x 1+y9=1,得y+9x=xy, ∴(x-1)(y-9)=9.∴x+y=10+(x-1)+(y-9)≥10+2)9)(1(--y x =16,当且仅当x-1=y-9时取得等号.又x 1+y9=1, ∴x=4,y=12.∴当x=4,y=12时,x+y 取得最小值16.绿色通道:本题给出了三种解法,都用到了基本不等式,且都对式子进行了变形,配凑出基本不等式满足的条件,这是经常需要使用的方法,要学会观察,学会变形,另外解法二,通过消元,化二元问题为一元问题,要注意根据被代换的变量的范围对另外一个变量的范围的影响.黑色陷阱:本题容易犯这样的错误:x 1+y 9≥2xy 9①,即xy6≤1,∴xy ≥6. ∴x+y≥2xy ≥2×6=12②.∴x+y 的最小值是12. 产生不同结果的原因是不等式①等号成立的条件是x 1=y9,不等式②等号成立的条件是x=y.在同一个题目中连续运用了两次基本不等式,但是两个基本不等式等号成立的条件不同,会导致错误结论.变式训练已知正数a,b,x,y 满足a+b=10,y b x a +=1,x+y 的最小值为18,求a,b 的值. 思路分析:本题属于“1”的代换问题.解:x+y=(x+y)(y b x a +)=a+x ay y bx ++b=10+xay y bx +. ∵x,y >0,a,b >0,∴x+y≥10+2ab =18,即ab =4.又a+b=10,∴⎩⎨⎧==8,2b a 或⎩⎨⎧==.2,8b a 例3求f(x)=3+lgx+x lg 4的最小值(0<x <1). 思路分析:∵0<x <1,∴lgx <0,xlg 4<0不满足各项必须是正数这一条件,不能直接应用基本不等式,正确的处理方法是加上负号变正数.解:∵0<x <1,∴lgx <0,x lg 4<0.∴-xlg 4>0. ∴(-lgx)+(-x lg 4)≥2)lg 4)(lg (xx --=4. ∴lgx+x lg 4≤-4.∴f(x)=3+lgx+xlg 4≤3-4=-1. 当且仅当lgx=x lg 4,即x=1001时取得等号. 则有f(x)=3+lgx+xlg 4 (0<x <1)的最小值为-1. 黑色陷阱:本题容易忽略0<x <1这一个条件.变式训练1已知x <45,求函数y=4x-2+541-x 的最大值. 思路分析:求和的最值,应凑积为定值.要注意条件x <45,则4x-5<0. 解:∵x <45,∴4x-5<0. y=4x-5+541-x +3=-[(5-4x)+x 451-]+3 ≤-2x x 451)45(-∙-+3=-2+3=1. 当且仅当5-4x=x451-,即x=1时等号成立. 所以当x=1时,函数的最大值是1.变式训练2当x <23时,求函数y=x+328-x 的最大值. 思路分析:本题是求两个式子和的最大值,但是x·328-x 并不是定值,也不能保证是正值,所以,必须使用一些技巧对原式变形.可以变为y=21(2x-3)+328-x +23=-(x x 238223-+-)+23,再求最值.解:y=21(2x-3)+328-x +23=-(x x 238223-+-)+23, ∵当x <23时,3-2x >0, ∴x x 238223-+-≥xx 2382232-∙-=4,当且仅当x x 238223-=-,即x=-21时取等号. 于是y≤-4+23=25-,故函数有最大值25-. 例4如图3-4-1,动物园要围成相同的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.图3-4-1(1)现有可围36 m 长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?(2)若使每间虎笼面积为24 m 2,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋总长度最小?思路分析:设每间虎笼长为x m ,宽为y m ,则(1)是在4x+6y=36的前提下求xy 的最大值;而(2)则是在xy=24的前提下来求4x+6y 的最小值.解:(1)设每间虎笼长为x m ,宽为y m ,则由条件,知4x+6y=36,即2x+3y=18.设每间虎笼的面积为S ,则S=xy.方法一:由于2x+3y≥2y x 32⨯=2xy 6,∴2xy 6≤18,得xy≤227,即S≤227. 当且仅当2x=3y 时等号成立.由⎩⎨⎧=+=,1832,22y x y x 解得⎩⎨⎧==.3,5.4y x 故每间虎笼长为4.5 m ,宽为3 m 时,可使面积最大. 方法二:由2x+3y=18,得x=9-23y. ∵x >0,∴0<y <6. S=xy=(9-23y)y=23 (6-y)y. ∵0<y <6,∴6-y >0.∴S≤23[2)6(y y +-]2=227. 当且仅当6-y=y,即y=3时,等号成立,此时x=4.5.故每间虎笼长4.5 m,宽3 m 时,可使面积最大.(2)由条件知S=xy=24.设钢筋网总长为l,则l=4x+6y.方法一:∵2x+3y≥2y x 32∙=2xy 6=24,∴l=4x+6y=2(2x+3y)≥48,当且仅当2x=3y 时,等号成立.由⎩⎨⎧==,24,32xy y x 解得⎩⎨⎧==.4,6y x 故每间虎笼长6 m ,宽4 m 时,可使钢筋网总长最小.方法二:由xy=24,得x=y24. ∴l=4x+6y=y 96+6y=6(y 16+y)≥6×2y y⨯16=48,当且仅当y 16=y ,即y=4时,等号成立,此时x=6. 故每间虎笼长6 m,宽4 m 时,可使钢筋总长最小.绿色通道:在使用基本不等式求函数的最大值或最小值时,要注意:(1)x,y 都是正数;(2)积xy (或x+y )为定值;(3)x 与y 必须能够相等,特别情况下,还要根据条件构造满足上述三个条件的结论.变式训练某工厂拟建一座平面图为矩形且面积为200 平方米的三级污水处理池(平面图如图3-4-2所示),由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两道隔墙建造单价为每米248元,池底建造单价为每平方米80元,池壁的厚度忽略不计,试设计污水处理池的长和宽,使总造价最低,并求出最低造价.图3-4-2思路分析:在利用均值不等式求最值时,必须考虑等号成立的条件,若等号不能成立,通常要用函数的单调性进行求解.解:设污水处理池的长为x 米,则宽为x 200米(0<x≤16,0<x200≤16),∴12.5≤x≤16. 于是总造价Q(x)=400(2x+2×x 200)+248×2×x 200+80×200. =800(x+x 324)+16 000≥800×2xx 324∙+16 000=44 800, 当且仅当x=x324 (x >0),即x=18时等号成立,而18∉[12.5,16],∴Q(x)>44 800. 下面研究Q(x)在[12.5,16]上的单调性.对任意12.5≤x 1<x 2≤16,则x 2-x 1>0,x 1x 2<162<324.Q(x 2)-Q(x 1)=800[(x 2-x 1)+324(1211x x -)] =800×212112)324)((x x x x x x --<0, ∴Q(x 2)>Q(x 1).∴Q(x)在[12.5,16]上是减函数.∴Q(x)≥Q(16)=45 000.答:当污水处理池的长为16米,宽为12.5米时,总造价最低,最低造价为45 000元.问题探究问题某人要买房,随着楼层的升高,上下楼耗费的精力增多,因此不满意度升高.当住第n 层楼时,上下楼造成的不满意度为n.但高处空气清新,嘈杂音较小,环境较为安静,因此随着楼层的升高,环境不满意度降低.设住第n 层楼时,环境不满意程度为n8.则此人应选第几楼,会有一个最佳满意度. 导思:本问题实际是求n 为何值时,不满意度最小的问题,先要根据问题列出一个关于楼层的函数式,再根据基本不等式求解即可.探究:设此人应选第n 层楼,此时的不满意程度为y.由题意知y=n+n8.∵n+n 8≥2248=⨯n n ,当且仅当n=n 8,即n=22时取等号.但考虑到n ∈N *,∴n≈2×1.414=2.828≈3,即此人应选3楼,不满意度最低.。
