高等动力学2.2
高等动力学

T T0 T1 T2
式中
(1.3.20)
1 l l T2 a jk q j qk 2 j 1 k 1
1 T0 a0 2
T1 a j q j
j 1
l
(1.3.21)
分别为广义速度 q j ( j 1, 2,..., l )的零次、一次、二次齐函数。用动能Fra bibliotek示的动力学普遍方程
韩伟
用动能表示的动力学普遍方程
仍讨论N个质点 Pi(i 1, 2,..., N ) 组成的带有r个完整约束 和s个非完整约束的系统, 选取l 3N r 个广义坐标 q j ( j 1, 2,..., l ) 表示系统的位形, 系统的自由度为 f 3N r s 。 各质点的矢径 ri (i 1, 2,..., N )由广义坐标完全确定,
(1.3.22)
质点系具有定常约束时,ri t 0 ,即 a0 a j 0, a jk 中不显含时间, 则有
T T2
(1.3.23)
因此定常约束情况下质点系的动能是广义速度的二次齐函数。
谢谢大家!
(i 1, 2,..., N ; j 1, 2,...l )
(1.3.16a)
将 ri 对某个广义坐标 q j 求偏导数,并交换对时间t求导的次序, 导出第二个恒等式
ri d ri ( ) q j dt q j
(i 1, 2,...N ; j 1, 2,...l )
(1.3.16b)
(1.3.17)
式中T为质点系的动能
1 T mi ri i r i 1 2
N
(1.3.18)
将式(1.3.4)和(1.3.17)代入式(1.3.13),得到用动能 表示的动力学普遍方程
高等动力学 第二章 2.3

例2.6 在倾角为α 的冰面上运动的冰刀,简化为长度 为l的均质杆AB,其质心0c的速度方向保持与刀刃AB一 致。试利用阿佩尔方程建立冰刀的运动微分方程。
解:将广义坐标中的xc,ϑ的
导数取作准速度,令
,从例1.3给 c,u 2 u1 x 出的约束方程解出 c x c tan (a) y
与广义坐标xc,yc,ϑ对应的广义力依次为
Q1 0,Q2 -mgsin ,Q3 0
代入式(2.3.16),令h11=1,
(b)
h12=tanϑ,h32=1,其余hjv为零, 导出
~ ~ Q1 mgsin tan,Q2 0 (c)
将约束方程(a)对t微分一次,化作
2 yc xc tan xc sec
(c)
将式(a)和(c)代入阿佩尔方程(2.3.19),得到 与例1.10相同的运动微分方程。
3.刚体的加速度能量
刚体内质量为 mi的质点的加速度 ri可分解为 i 质心加速度 rc和由转动引起的相对加 速度 p i c i (2.3.20) r r p
将式(2.3.8)对t再微分一次。得到
ri
l j 1
i r j (与q j无关项 ) (i 1 q , 2, ,N)(2.3.11 ) j q
利用上式及P20(1.3.16a)导出
i ri ri r j q j qj q (i 1 , 2, ,N;j 1, 2, ,l ) (2.3.12)
将式(2.3.9),(2.3.10)和(2.3.12)代入动力 学普遍方程(2.3.7),适当改变求和顺序,得到
l N
f
[
(
高等大气动力学讲义

高等大气动力学讲义(第三稿)第一章引论1、大气动力学的内容,方法和意义2、高等大气动力学讲述的主要内容3、大气动力学发展(简)史1、大气动力学的内容,方法和意义1.1内容大气动力学把地球(行星)大气作为连续介质(流体),用流体力学、热力学定律研究其中发生的各种尺度的宏观运动,总结运动规律,探索运动的机制,为预测大气的运动提供理论基础。
高等大气动力学:对物理内涵的阐释更加精准,使用的数学方法更加严谨,得出的结论更具普遍意义及一般性。
该课程与大学所修“动力气象学”之关系,类似普通物理学与理论物理学之关系。
大气(地球流体)大尺度运动与普通流体之运动主要异处有三:①层结性:层结性使之更具“弹性”;②旋转性:旋转性使之更具“刚性”;③斜压性:斜压性使之更具“活性”。
此为地球流体(大气与海洋)大尺度运动之主要特性,此外,大气运动还有以下独特属性:④气压场(质量场)、温度场、湿度场均与流场耦合,而非相互独立;⑤不同时空尺度的运动之间存在复杂的非线性相互作用。
就大气运动而言,水汽相变至为重要且困难;辐射过程为另一重要且复杂之过程。
这些过程令大气运动之动力过程与热力过程相耦合,能量过程与物质过程相耦合,使问题复杂化,然亦令大气运动运动丰富且独特。
此外,非线性过程令不同尺度(时间尺度、空间尺度)之运动间耦合,亦使大气运动复杂而多彩。
大气中各种时空尺度的运动规律及其物理机制,不同时空尺度运动间的相互作用,是大气动力学研究的核心内容。
本课程主要关注大气的大尺度运动。
图1.1 该图给出了辐射传输、水汽过程、大气运动等热力、动力过程的耦合。
大气辐射过程与大气中的水汽含量和分布密切相关,水汽的分布状况有强烈依赖于大气运动,而大气的运动多于热源强迫有关,热源的状况本质上又是辐射过程决定。
如此以来,热力过程与动力过程相耦合,形成一个相互作用的复杂的系统。
复杂系统往往较为稳定,形成观测到的相对稳定的气候。
1.2 方法①观测(实验)研究:获得(收集)观测资料加以分析,去粗取精,去伪存真,发现最核心的物理现象,提出科学问题。
高等动力学课程总结

高等动力学课程总结刚进入博士一年级,所参与的课题是水下机器人的控制研究,进入课题组的时候,所涉及到的相关课题中的涉及到的很多的运动系统模型基本不知所以然,看了很多关于水下机器人的书籍和文献,但是对其中的一些物理量也缺乏明确认知。
很是庆幸的是开学的时候听从了师兄的意见选修了《高等动力学》的课程,通过这一学期的学习,对分析力学、刚体力学等有了一些了解,对后续的课题研究打下了扎实的基础。
《高等动力学》课程主要包括三个部分的内容,分别是分析力学,刚体力学和稳定性理论。
分析力学通过引入广义坐标将传统矢量力学的矢量分析方法转化为直接运用数学分析的方法,研究宏观现象中的力学问题。
分析力学的是独立于牛顿力学的描述力学世界的体系;刚体力学包括刚体运动学和刚体动力学两个基本部分内容,主要讲述特殊质点系-刚体在外力作用下的运动规律;运动稳定性理论则主要介绍了稳定性的基本分析方法和判别方法及思路。
分析力学分析力学的最基本出发点是引入了广义坐标的概念,并利用约束的概念建立了广义坐标变量之间的相互关系,即约束方程。
在此基础上,引入了与矢量力学中牛顿动力学基本定律相对应的动力学普遍方程。
此后在动力学普遍方程的基础上通过不同的变化与数学推导,引出了适用于完成系统的拉格朗日第二类方程,哈密顿正则方程、罗斯方程和适用于非完整系统的拉格朗日第一运动方程、劳斯方程、阿贝尔方程和凯恩方程,在引入各方程的过程中引入了相对应的常见动力学量的广义坐标形式和广义动力学量。
相比于经典力学中矢量力学分析方法,分析力学在分析过程中,完全避免了约束力在方程中出现,极大程度上减小了方程处理的难度。
刚体动力学刚体的一般运动可以分解为随质心运动的平移和相对质心的转动。
刚体的平移可直接利用质心运动定理转化为质点动力学问题,因而刚体绕定点的转动是刚体动力学的主要内容。
其主要内容包括刚体绕定点转动的运动学和动力学两大部分。
稳定性理论稳定性理论课程中,主要介绍了运动稳定性理论、Lyapunov 直接法、保守系统的平衡位置与定常运动稳定性、力的结构一起对运动稳定性的影响。
高等结构动力学2

t
p (τ )
数值积分递推计算公式:v N = AN sin ω D t N − B N cos ω D t N 矩形公式: 曲边梯形:
AN = AN −1 exp( −ξω∆τ ) +
二次曲线: AN = AN −2 exp(−ξω∆τ )
+ ∆τ 3mω
∆τ y N −1 exp(−ξω∆τ ) mω D ∆τ [ y N −1 exp(−ξω∆τ ) + y N ] AN = AN −1 exp( −ξω∆τ ) + 2 mω D
FFT计算法则(续) ③ WNnm计算方法
(2 nm WN = WN
γ −1
nr −1 + 2γ − 2 nr − 2 +L+ n0 )( 2γ −1 mr −1 + 2γ − 2 mr − 2 +L+ m0 )
∵
a +b a b WN = WN WN
∴ W
nm N
=W
( 2γ −1 nr −1 + 2γ − 2 nr − 2 +L+ n0 )( 2γ −1 mr −1 ) N
1.1 无阻尼精确解(续)
广义卷积(General Convolution Integral):
v(t ) = p(τ )h(t − τ )dτ
0
∫
t
(t ≥ 0)
单位脉冲响应函数(Unit-Impulse Response Function):
高等结构动力学

SC — 地基土对地震谱影响
ξ — 阻尼比
T — 周期
同济大学土木工程防灾国家重点实验室、桥梁工程系
3.1确定合适的地震输入(续) ¾响应谱简化 S = S (SC ,ξ , T )
结论:地震土越硬,卓越周期越小,带宽越小
同济大学土木工程防灾国家重点实验室、桥梁工程系
&& }+ [C ]{∆δ & }+ [K ]{∆δ } = {∆p(t )}+ {p T (t )} [M ss ]{∆δ vs ss vs ss vs
&& }− ([C ]{∆δ& }+ [C ]{∆δ& }) {∆p(t )} = −[M ss ]{∆δ ps ss ps sg g
&& (t )}− [C ]{∆δ& (t )}− {F (t )} {p (t )} = {p(t )}− [M ]{∆δ
概率性线性地震反应分析 各态平稳随机过程 自相关函数、功率谱密度、概率分布 概率性非线性地震反应分析
同济大学土木工程防灾国家重点实验室、桥梁工程系
小结
桥梁地震反应分析
实际地震波输入 确定合适的地震输入 模拟地震波输入 分步计算增量方程 建立系统的数学模型 静力平衡解耦方程 非线性地震时程分析 选择有效的求解方法 逐步积分法求解
同济大学土木工程防灾国家重点实验室、桥梁工程系
1. 桥梁抗震设计现状(续)
1.3 引起震害原因
¾地震问题 砂土液化、地基下沉、岸坡滑移或开裂 ¾结构问题 形式、构造或连接措施不当引起的落梁 ¾地震力分布问题 桥梁各支承点的地面运动不一致 ¾设计问题 墩柱本身抗震能力不足造成的破坏
大学精品课件:动力学2-2
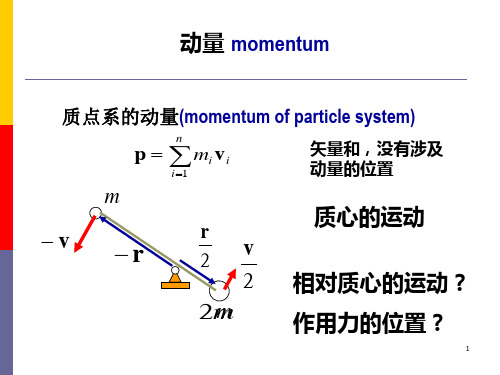
质点系的动量(momentum of particle system)
n
p mi vi i 1
矢量和,没有涉及 动量的位置
m
v r
r
2v 2
质心的运动 相对质心的运动?
2mm
作用力的位置?
1
2
动量的‘位置’ 、力的‘位置’
mv
mv
5m
5m
3
动量矩 Moment of momentum (Angular momentum)
yivix )
7
平移刚体的动量对O点之矩 有无意义?
n
mi
v
vC
Lo (ri mi vi ) i 1 n
z
ri rC
(ri mi vC ) i 1 n
( miri ) vC i 1
o
y
x
(mrC ) vC
rC (mvC )
8
定轴转动刚体的动量矩
zik rxy
ri
O
n
n
Lo (ri mi v) miri (k ri )
i 1
i 1
n
n
ri '(miaC ) ( miri) aC
i 1
i 1
17
例:半径为R,质量为m的均质圆盘,静止放在光滑地面上,其 上作用有力偶,如图所示,求在力偶作用下质心的加速度,角加 速度。
y
F C
xF
解:由质心运动定理
maC 0 vC 0 rC 0
由相对质心的动量矩定理
i 1
i 1
ri zk rxy k ri k rxy
n
Lo mi (zkk rxy) (k rxy )
高等动力学2

δW (Q
j 1
k
j
Q gj )δq j 0
广义虚位移q1、q2、…、qk独立且任意
Q j Q gj 0
j 1,2, , k
上式表明质点系的动力学普遍方程也可表示为 广义力与广义惯性力之和等于零。它是代数方程, 其数目等于系统的自由度数。
(3)拉格朗日方程
n 1 1 2 l r l T ml v l ml r l 1 2 l 1 2 k r r rl 1 k rl l l q q mi i j q q t t 1 l 1 2 i i j 1 j k 1 k k i q j bi q i c aij q 2 i 1 j 1 i 1 n n
高等动力学
应祖光
yingzg@
第二章 拉格朗日方程
1 2 3 4 第二类拉格朗日方程 拉格朗日方程的应用 耗散力与陀螺力 能量积分与循环积分
1.第二类拉格朗日方程
(1)动力学普遍方程
质点系由n个质点组成,受到s个完整约束,系统自由 度为k=3n-s。 取广义坐标q1、q2、…、qk,任一质点的矢量坐标通过 广义坐标表示为ri=ri(q1,q2,…,qk;t)。 质点的质量为mi,受到主动力Fi与约束力Fci作用,再 加上惯性力 F gi mi a i 。 根据达朗贝尔原理,质点系的所有主动力、约束力和惯 性力在形式上组成平衡力系,满足平衡条件。
d T dt q j
T Qj q j
j 1,2, , k
它是常微分形式的方程,其数目等于系统的自由 度数。 该方程由系统动能与广义力确定,它们都是代数 量、计算方便。 对于受理想约束的系统,该动力学方程不包含未 知的约束力,故没有“多余”的动力学关系。 如果需求约束力,可解除相应的约束,将约束力 转化为主动力,从而通过广义力进入拉格朗日方 程,同时系统的自由度或方程数也随之增加。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L/O/G/O
THANK YOU!
f 1 x12 x 2 2 x3 2 l 2 0 f2( bx1 bx2 bx3 b) 2 ( h) 2 ( ) 2 h 2 0 l l l
写出此约束方程的变分形式:
x1x1 x 2x 2 x3x3 0 b 2 ( x1 l )x1 b(bx2 hl)x 2 b 2 x3x3 0
ki i i 1
3N
(k 1,2,..., r s)
xi dxi dxi
*
**
(2.2.2)
具有理想双侧约束的质点系在 运动的任意瞬时,其主动力和 惯性力在系统的任意虚位移中 系统内各质点的运动必须满足动力学普遍方程 所做的元功之和等于零。
(F m r ) r 0
(上一章中导出的拉格朗日方程(1.3.30)也 称为第二类拉格朗日方程)
2.拉格朗日乘子的物理意义
设一质点在固定面f(x1,x2,x3)=0上运动,取λ 为拉格朗日乘子,则第一类拉格朗日方程为
f Fi mi x i ( ) 0 xi
(i 1,2,3)
或写作
mi x i Fi (
Fi mi x i kAki 0
k 1
r s
(i 1,2,..., 3N )
(2.2.5)
此包含r+s个未定乘子的方程组(2.2.5)称为第一 类拉格朗日方程,未定乘子λk(k=1,2,…,r+s)称为 拉格朗日乘子。 由于方程中除待定的各质点坐标xi (i=1,2,…,3N)以 外,又增加了待定的拉格朗日乘λk(k=1,2,…,r+s),共 有3N +r+s个未知变量,因此还必须同时列出r个完 整约束方程(1.1.2)和s个线性非完整约束(1.1.6) 才能使方程组封闭。
例2.3长度为l的无质量直杆一端用球铰O与支座固 定,如图示, 另一端固定一质量为m的小球A,长度为h的软绳一端固定于点C, 另一端固定于杆上的点B,BO的距离为b,平衡时OA水平,而BC 垂直。试用拉格朗日乘子法建立小球的运动微分方程。
解:小球具有一个自由度,设小球的坐标 为 x1, x2, x3 , 则点B的坐标为bx1 / l , bx2 / l , bx3 / l 由于OA和BC的长度不变,可列出两个约束方 程
f ) (i 1,2,3) xi
将上式与牛顿第二定律
mi x i Fi Ni (i 1,2,3)
相比较得到
f ( ) Ni (i 1,2,3) xi
从而看出拉格朗日乘子正比于约束力。这表明在 动力学普遍方程中已被消去的理想约束力通过拉 格朗日乘子又被引回来了。因此,利用第一类拉 格朗日方程可同时解出系统的约束力。 (虽然这种方法的未知变量和方程都增多, 但由于计算过程极为程式化,在计算技术高 度发展的今天,第一类拉格朗日方程又重新 受到重视,在工程技术得到实际应用。)
2.2拉格朗日乘子法
2.2拉格朗日乘子法
1 2
第一类拉格朗日方程 拉格朗日乘子法的物理意义
3
劳斯方程
不含多余坐标的 完整系统
拉格朗日方程
哈密顿正则方程
拉格朗日乘子法是处理非完整系统的一种方法,本 章介绍的第一类拉格朗日方程和劳斯方程都是拉格 朗日乘子法的具体应用,区别在于前者使用笛卡尔 坐标,后者使用广义坐标。
fk Aki xi
m x 2 F 2 1 A12 2 A22 f 1 f 2 F 2 1 2 x 2 x 2 mg 1 x 2 2b(bx2 hl)
m x3 F 3 1 A13 2 A23 f 1 f 2 F 3 1 2 x3 x3 2 1 x 3 2b x 3
f 2 b(bx2 hl) x 2
f 2 b 2 ( x1 l ) x1
f 2 b 2 x3 x3
m x1 F 1 1 A11 2 A21 f 1 f 2 F 1 1 2 x1 x1 2 1 x1 2b ( x1 l )
小球A受到的主动力为重力,沿轴 x 2的负方向,即有
F 1 0, F 2 mg , F 3 0
将式(b)分别乘以 导出
1, 2 ,代入第一个拉格朗日方程,
m x1 1 x1 2b 2 ( x1 l ) m x 2 mg 1 x1 2b(bx2 hl) m x 3 1 x 3 2b 2 x 3
推导过程
x1x1 x 2x 2 x3x3 0 b 2 ( x1 l )x1 b(bx2 hl)x 2 b 2 x3x3 0
f 1 f 1 f 1 x1 x2 x3 x1 x 2 x3 f 1 f 1 f 1 x1 x2 x3 x1 x 2 x3
1.第一类拉格朗日方程
设质点系由N个质点Pi(i=1,2,…N)组成,以3N个 笛卡尔坐标确定其位形。设系统存在r个完整约 束和s个线性非完整约束,约束方程统一写成
A dx A
ki i i 1
3N
k0
dt 0 (k 1,2,..., r s)
也可以写作关于虚位移的约束条件
A x 0
引入r+s个未定乘子λk,分别与式(2.2.2)中 标号相同的各式相乘,然后将它们的和式与式 (2.2.3)相加,得到
(F m x A
i i i k i 1 k 1
3N
rs
ki
) xi 0
(2定乘子λk ,使式 (2.2.4)中r+s个实现指定为不独立变分 i x (i=1,2,…,r+s)前的系数等于零,可得到 r+s个方程。 于是在方程(2.2.4)中只包含f个与独立变分 xi (i=r+s+1,r+s+2,…,3N)有关的和式。 这f个变分既然是独立变量,则方程(2.2.4) 成立的充分必要条件就是各坐标变分前的系数 等于零,共得到f个方程,连同已得到的r+s个 方程,总共可列出f+r+s=3N个方程:
i i i i i 1
N
将主动力Fi(i=1,2,…N)相对某个参考坐标系的3N 个分量依次排列为Fi(i=1,2,…3N),则动力学普遍 方程的标量形式为
( F m x ) x 0
i i i i i 1
3N
(2.2.3)
xi 由于r+s个约束条件的存在,在3N个坐标变分 中只有f=3N-r-s个独立变量,至于3N个坐标变分中哪些 是独立的,则可以任意指定。
