第二章财务管理基础
第二章 财务管理基础

【例题·多选题】(2018 年试卷 2)关于资本资产定价模型,下列说法正确的( )。 A.该模型反映资产的必要收益率而不是实际收益率 B.该模型中的资本资产主要指的是债券资产 C.该模型解释了风险收益率的决定因素和度量方法 D.该模型反映了系统性风险对资产必要收益率的影响
【例题·多选题】下列关于资本资产定价模型β系数的表述中,正确的有( A.β系数可以为负数 B.β系数是影响证券收益的唯一因素 C.投资组合的β系数一定会比组合中任一单只证券的β系数低 D.β系数反映的是证券的系统风险
A.两项资产的收益率之间不存在相关性 B.无法判断两项资产的收益率是否存在相关性 C.两项资产的组合可以分散一部分非系统性风险 D.两项资产的组合可以分散一部分系统性风险
【例题·多选题】下列关于证券投资组合的表述中,正确的有( A.两种证券的收益率完全正相关时可以消除风险 B.投资组合收益率为组合中各单项资产收益率的加权平均数 C.投资组合风险是各单项资产风险的加权平均数 D.投资组合能够分散掉的是非系统风险
A.0.29% B.22.22% C.14.29% D.0.44%
【例题·单选题】(2018 年试卷 1)某公司购买一批贵金属材料,为避免资产被盗而造 成的损失,向财产保险公司进行了投保,则该公司采取的风险对策( )。
A.规避风险 B.接受风险 C.转移风险 D.减少风险
【例题·单选题】下列各种风险应对措施中,能够转移风险的是( A.业务外包 B.多元化投资 C.放弃亏损项目
【例题·多选题】下列各项中,属于固定成本项目的有( A.采用工作量法计提的折旧 B.不动产财产保险费 C.直接材料费 D.写字楼租金
)。
【例题·多选题】下列各项中,属于约束性固定成本的有( )。 A.管理人员薪酬 B.折旧费 C.职工培训费 D.研究开发支出
2020中级会计 财管 第二章 财务管理基础
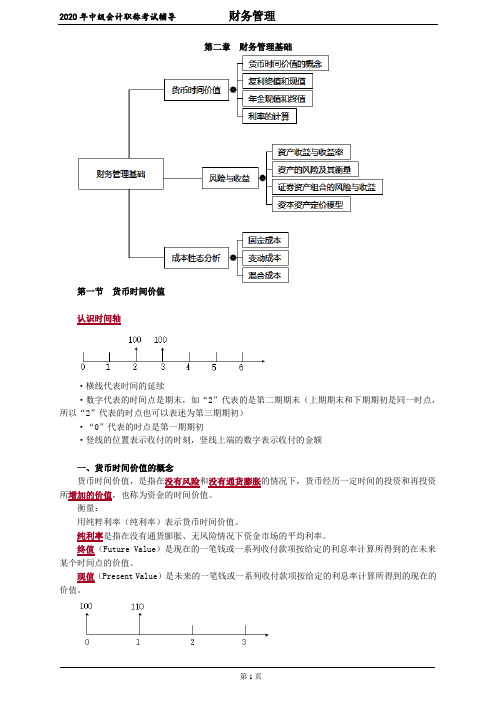
第二章财务管理基础第一节货币时间价值认识时间轴·横线代表时间的延续·数字代表的时间点是期末,如“2”代表的是第二期期末(上期期末和下期期初是同一时点,所以“2”代表的时点也可以表述为第三期期初)·“0”代表的时点是第一期期初·竖线的位置表示收付的时刻,竖线上端的数字表示收付的金额一、货币时间价值的概念货币时间价值,是指在没有风险和没有通货膨胀的情况下,货币经历一定时间的投资和再投资所增加的价值,也称为资金的时间价值。
衡量:用纯粹利率(纯利率)表示货币时间价值。
纯利率是指在没有通货膨胀、无风险情况下资金市场的平均利率。
终值(Future Value)是现在的一笔钱或一系列收付款项按给定的利息率计算所得到的在未来某个时间点的价值。
现值(Present Value)是未来的一笔钱或一系列收付款项按给定的利息率计算所得到的现在的价值。
单利是指按照固定的本金计算利息的一种计息方式。
按照单利计算的方法,只有本金在贷款期限中获得利息,不管时间多长,所生利息均不加入本金重复计算利息。
复利是指不仅对本金计算利息,还对利息计算利息的一种计息方式。
二、复利终值和现值计算(一)复利终值计算【例题·计算分析题】若将1 000元以3%的利率存入银行,则3年后的本利和是多少?F=P×(1+i)n其中:(1+i)n为复利终值系数,用(F/P,i,n)表示。
F=P×(F/P,i,n)『正确答案』F=P×(F/P,i,n)=1 000×(F/P,3%,3)=1 000×1.0927=1 092.7(元)(二)复利现值计算由F=P×(1+i)n得:=F×(1+i)-n=F×(P/F,i,n)其中:(P/F,i,n)为复利现值系数,与复利终值系数互为倒数。
【例题·计算分析题】假设甲存入银行一笔钱,以3%的利率计息,想在3年后得到1 000元,则现在需存入银行多少钱? 已知:(P/F,3%,3)=0.9151『正确答案』P=F×(P/F,i,n)=1 000×(P/F,3%,3)=1 000×0.9151=915.1(元)三、年金终值和现值年金,是指间隔相等的系列等额收付款项。
第二章财务管理基础.docx

第二章财务管理基础.docx第二章财务管理基础本章考情分析本章属于财务管理的计算基础,主要为后续章节的学习打基础,本章的内容非常重要,另外本章属于财务管理的第一个难点。
从考试的情况来看,本章近三年的平均分值为6分,涉及的题型有客观题和主观题。
主要考点包括货币时间价值及其系数之间换算、风险衡量指标及其计算、投资组合收益率和投资组合标准差的计算、资本资产定价模型的应用等。
第一节货币时间价值一、货币时间价值的概念货币时间价值是指没有风险和没有通货膨胀情况下,货币经历一定时间的投资和再投资所增加的价值,也称为资金的时间价值。
实务中,习惯用相对数字表示货币时间价值,即增加的价值占投入货币的百分数表示;用相对数表示的货币时间价值也称为纯粹利率(纯利率),纯利率是指没有通货膨胀、无风险情况下的资金市场的平均利率,没有通货膨胀时,短期国库券的利率可以视为纯利率。
货币时间价值=社会平均报酬率-风险报酬率-通货膨胀率例:①1980年的10万元与2018年的10万哪个价值更高?②1980年的10万元与2018年的100万哪个价值更高?二、复利现值与终值复利计算方法是指每经过一个计息期,要将该期的利息加入本金再计算利息。
(一)相关概念1.终值又称将来值,是现在一定量的货币折算到未来某一时点所对应的金额,通常用字母F表示。
2.现值,是指未来某一时点上一定量的货币折算到现在所对应的金额,通常用字母P表示。
现值和终值是一定量货币在前后两个不同时点上对应的价值,其差额即为货币的时间价值。
3.计算利息的期数现值和终值对应的时点之间划分为的计算利息的期数,划分时相邻两次计息的间隔,如年、月、日,除非特别说明,一般为1年,通常用字母n表示。
4.利率利率为货币时间价值的一种具体表现,也称为折现率。
通常用字母i表示,利息用字母I表示。
如无特殊说明,利率/折算率/报酬率一般指年利率,不足一年的按360天折算。
6.计息方式①单利按照固定的本金计算利息的一种计息方式,所生利息均不加入本金重复计算利息。
第二章 财务管理基础

第二章财务管理基础本章知识框架货币的时间价值的含义一次性收付款项的终值和现值年金概述货币时间价值普通年金终值与普通年金现值预付年金终值与预付年金现值递延年金与永续年金的现值利率和期间的推算名义利率和实际利率财务管理基础资产的收益和收益率风险与收益资产的风险及其衡量证券资产组合的风险与收益资本资产定价模型固定成本成本性态变动成本混合成本混合成本的分解方法本章内容讲解第一节货币时间价值一、货币的时间价值的含义货币的时间价值,指一定数量的货币在不同时点上价值量的差额。
二、一次性收付款项的终值和现值(一)终值和现值的概念四、普通年金终值与普通年金现值A(1+i)4A(1+i)3 A(1+i)2 A(1+i)1 A(1+i)00 1 2 3 4 5 普通年金终值定义公式:F =A(1+i)0 +A(1+i)1 +A(1+i)2 +......+ A(1+i)n-1 ①将上式左右两边同时乘以(1+i),等式不变,得:F + Fi=A(1+i)1 +A(1+i)2 +A(1+i)3+......+ A(1+i)n② 将二式减去一式,左边减左边,右边减右边,等式不变,得:Fi=A(1+i)n -A(1+i)0整理上式,得:F =A ×[(1+i)n -1]/i=A ×(F /A ,i ,n)关于普通年金现值公式的推导: A1)1(1i + A 2)1(1i + A 3)1(1i + A 4)1(1i + A 5)1(1i +0 1 2 3 4 5普通年金现值定义公式:P=A(1+i)-1 +A(1+i)-2 +A(1+i)-3 +......+ A(1+i)-n ①将上式左右两边同时乘以(1+i),等式不变,得:P+Pi=A(1+i)0 +A(1+i)-1 +A(1+i)-2 +......+ A(1+i)-(n-1)②将二式减去一式,左边减左边,右边减右边,等式不变,得:Pi=A(1+i)0- A(1+i)-n整理上式,得:P=A×[1-(1+i)-n]/i=A×(P/A,i,n)互为倒数关系的四组系数:(1)单利终值系数与单利现值系数(2)复利终值系数与复利现值系数。
会计中级考试财务管理科目第二章 财务管理基础(带答案)

第二章财务管理基础一、单项选择题1、某企业于年初存入银行10 000元,假定年利息率为12%,每年复利两次。
已知(F/P,6%,5)=1.3382,(F/P,6%,10)=1.7908,(F/P,12%,5)=1.7623,(F/P,12%,10)=3.1058,则第5年末的本利和为()元。
A、13 382B、17 623C、17 908D、31 0582、一项600万元的借款,借款期3年,年利率为10%,若每半年复利一次,则年实际利率为()。
A、10%B、5%C、10.25%D、10.75%3、下列关于β系数的表述中,不正确的是()。
A、β系数可以为负数B、市场组合的β系数等于1C、投资组合的β系数一定会比组合中任一单项证券的β系数低D、β系数反映的是证券的系统风险4、某人从2015年年初开始,每年年初存入银行2万元,存款年利率为4%,按年复利计息,共计存款5次,在2019年年末可以取出()万元。
已知:(F/A,4%,5)=5.4163,(F/A,4%,6)=6.6330A、10.83B、11.27C、13.27D、13.805、某上市公司2013年的β系数为1.24,短期国债利率为3.5%。
市场组合的收益率为8%,则投资者投资该公司股票的必要收益率是()。
A、5.58%B、9.08%C、13.52%D、17.76%6、甲持有一项投资组合A和B,已知A、B的投资比重分别为30%和70%,相应的预期收益率分别为15%和20%,则该项投资组合的预期收益率为()。
A、21%B、18.5%C、30%D、10%7、已知(P/A,8%,5)=3.9927,(P/A,8%,6)=4.6229,(P/A,8%,7)=5.2064,则6年期、折现率为8%的预付年金现值系数是()。
A、2.9927B、4.2064C、4.9927D、6.20648、职工的基本工资,在正常工作时间情况下是不变的;但当工作时间超出正常标准,则需按加班时间的长短成比例地支付加班薪金,从成本性态的角度看,这部分人工成本属于()。
第二章+财务管理基础习题与答案

0.20 0.50 0.30
该公司所处行业风险价值系数为10%,无风险收益率为8%; 要求:⑴计算该方案的应得风险收益率和应得风险收益额; ⑵计算该方案的预测投资收益率、预测风险收益率和预测风险收益额; ⑶评价该投资方案是否可行。
3
PDF pdfFactory Pro
第二章 财务管理基础
1.某投资项目的投资额 10000 元,当年投资当年获益。各年年末的现金净流量如下: 年 份 1 2 3 1000 4 1000 5 2000 6 2000 7 2000 8 2000 9 2000 10 3000
现金流量 1000 1000
计算:在最低投资收益率为 8%的条件下,确定投资是否可行? 2.某公司现在向银行存入 10000 元,准备在若干年后获得 30000 元,假设银行存款利率为 8%,每年 复利一次,需要多少年后才能每年的还本付息额为 4600 元,则借款利率为多少? 4.某人拟于明年年初借款 42000 元,从明年年末开始,每年年末还本付息额均为 6000 元,连续 10 年还清。假设预期最低借款利率为 8%,问此人是否能按其预想的利率借到款项? 5.A股票和B股票在五种不同经济状况下预期报酬率的概率分布如下: 经济状况 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ 概率分布 0.2 0.2 0.2 0.2 0.2 A股票预期报酬率 30% 20% 10% 0 -10% B股票预期报酬率 -45% -15% 15% 45% 75%
③计算A股票报酬率的标准差
= (0.3 − 0.1) 2 × 0.2 + (0.2 − 0.1) 2 × 0.2 + (0.1 − 0.1) 2 × 0.2 + (0 − 0.1) 2 × 0.2 + (−0.1 − 0.1) 2 × 0.2 = 14.14%
2022会计师《财务管理》0201

2022会计师《财务管理》0201第二章财务管理基础考情分析本章主要介绍了货币时间价值、风险及成本性态等三部分内容,虽然属于基础性知识,但颇有难度,学习上应做好打硬仗的思想准备。
尤其是货币时间价值和成本性态,务必要予以理解并掌握。
本章题型以客观题和计算题为主。
估计本章2022年考分在6分左右。
最近三年本章考试题型、分值分布题型单选题多选题判断题合计2022年2题2分1题2分1题1分4题5分2022年2题2分2题4分1题1分5题7分2022年3题3分-1题1分4题4分知识框架第一节货币时间价值知识点一:货币时间价值的概念知识点二:一次支付的终值和现值知识点三:年金的终值和现值知识点四:利率的计算★知识点一:货币时间价值的概念一、货币时间价值的含义一定量货币在不同时点上的价值量差额。
“元”或“%”第1页2022年中级会计职称考试辅导财务管理(第二章)二、现值与终值的概念银行存款,多出来的利息就是该部分资金在某一段时间的货币时间价值。
三、利息计算的两种思路单利计息利不生利复利计息利生利、利滚利【例题】假如以单利方式借入1000元,年利率8%,四年末偿还,则各年利息和本利和,如表所示。
(单位:元)使用期1234年初款额1000108011601240年末利息1000某8%=80808080年末本利和1080116012401320年末偿还0001320★在以单利计息的情况下,总利息与本金,利率以及计息周期数成正比关系。
It=P某i单【例题】假如以复利方式借入1000元,年利率8%,四年末偿还,则各年利息和本利和,如表所示。
(单位:元)使用期1234年初款额100010801166.41259.712年末利息1000某8%=801080某8%=86.41166.4某8%=93.3121259.712某8%=100.777年末本利和10801166.41259.7121360.489年末偿还0001360.489★本金越大,利率越高,计息周期越多时,两者差距就越大。
第二章 财务管理基础(中级财务管理知识点与实例)

第二章财务管理基础考情分析:重点章节,以客观题和计算分析题形式考查。
分值6-8分。
第一节货币时间价值一、货币时间价值的概念货币时间价值是指:在没有风险和通货膨胀的情况下,货币经历一定时间的投资和再投资所增加的价值。
二、复利终值和现值复利是指:一次收付款项、多次收付款项但每次金额不相等。
(一)复利终值F=P×(F/P,i,n)【例】某人将100万元存入银行,年利率4%,半年计息一次,按照复利计算,求5年后的本利和。
答案:F=P×(F/P,2%,10)=100×(F/P,2%,10)=100×1.2190=121.90【例】某项目的建设工期为3年。
其中,第一年贷款400万元,第二年贷款500万元,第三年贷款300万元,贷款均为年初发放,年利率为12%。
若采用复利法计算建设期间的贷款利息,则第三年末贷款的本利和为()万元。
A.1525.17B.1361.76C.1489.17D.1625.17答案:A。
400×(F/P,12%,3)+500×(F/P,12%,2)+300×(F/P,12%,1)=1 525.17。
(二)复利现值P=F×(P/F,i,n)【例】某人拟在5年后获得本利和100万元。
假设存款年利率为4%,按照复利计息,他现在应存入多少元?答案:P=F×(P/F,4%,5)=100×(P/F,4%,5)=100×0.8219=82.19【例】随着折现率的提高,未来某一款项的现值将逐渐增加。
()答案:×。
在折现期间不变的情况下,折现率越高,折现系数越小,现值越小。
结论:(1)复利终值与复利现值互为逆运算;(2)复利终值系数(1+i)n与复利现值系数1/(1+i)n互为倒数(即复利终值系数×复利现值系数=1)。
【例】某人拟购置房产,开发商提出两个方案:方案一是现在一次性支付80万元;方案二是5年后支付100万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
假设单利计息,求5年后的终值。
『解答』F=P×(1+n×i)=100×(1+5×2%)= 110(元)
【例题2】某人为了5年后能从银行取出500元,在年 利率2%的情况下,目前应存入银行的金额是多少?
假设银行按单利计息。
『解答』P=F/(1+n×i)=500/(1+5×2%)=454.55
『正确答案』 12000×(P/A,i,3) = 30000 (P/A,i,3)=2.5 查年金现值系数表可得: 当i=10%时,(P/A,10%,3)=2.4869 当i=9%时,(P/A,9%,3)=2.5313 解之得:i=9.71% 如果分3次付清,3年支付款项的利率相当于9.71%,因此 更合算的方式是张先生按5%的利率贷款,现在一次付清。
【例题7】A矿业公司决定将其一处矿产10年开采权公开拍卖, 因此它向世界各国煤炭企业招标开矿。已知甲公司和乙公司的投 标书最具有竞争力,甲公司的投标书显示,如果该公司取得开采 权,从获得开采权的第1年开始,每年年末向A公司交纳10亿美 元的开采费,直到10年后开采结束。乙公司的投标书表示,该 公司在取得开采权时,直接付给A公司40亿美元,在第8年末再 付给60亿美元。如A公司要求的年投资回报率达到15%,问应接 受哪个公司的投标?
『解答』P=A×[(P/A,i,n-1)+1] =200×[(P/A,5%,2)+1] =200×(1.8594+1) =571.88(万元) P=A×(P/A,i,n)×(1+i) =200×(P/A,5%,3)×(1+5%) =200×2.7232×1.05 =571.87(万元) 公司应采用第一种支付方式。
『解答』(1)第一种付款方案属于预付年金,n=10 P=200×[(P/A,10%,9)+1]=200×6.7590= 1351.80(万元) 或:P=200×(P/A,10%,10)×(1+10%)= 1351.81(万元) (2)P=250×(P/A,10%,10)×(P/F,10%,3)= 1154.11(万元) 或:P=250×[(P/A,10%,13)-(P/A,10%,3)]= 1154.13(万元) 或:P=250×(F/A,10%,10)×(P/F,10%,13)= 1154.24(万元) 应该选择第二种方案。
【例题12】某企业向银行借入一笔款项,银行贷款的年利率 为10%,每年复利一次。银行规定前5年不用还本付息,但 从第6年至第20年每年年末偿还本息5000元。要求:用三种 方法计算这笔款项的现值。
P=5000×(P/A,10%,15)×(P/F,10%,5) =5000×7.6061×0.6209=23613.14(元) P=5000×[(P/A,10%,20)-(P/A,10%,5)] =5000×(8.5136-3.7908)=23614(元) P=5000×(F/A,10%,15)×(P/F,10%,20) =5000×31.772×0.1486=23606.60(元)
【例题14】归国华侨吴先生想支持家乡建设,特地在祖籍所在县 设立奖学金。奖学金每年发放一次,奖励每年高考的文理科状元 各10000元。奖学金的基金保存在中国银行该县支行。银行一年
的定期存款利率为2%。问吴先生要投资多少钱作为奖励基金?
『解答』由于每年都要拿出20000元,因此奖学金的性质是一 项永续年金。 其现值应为:20000/2%=1000000(元) 也就是说,吴先生要存入1000000元作为基金,才能保证 这一奖学金的成功运行。
以年利率12%等额偿还,则每年应付的金额为多少?
『解答』A=1000×(A/P,12%,10) =1000/(P/A,12%,10) =1000/5.6502
=176.98(万元)
【例题17· 单选题】甲希望在10年后获得100000元,已知银 行存款利率为2%,那么为了达到这个目标,甲从现在开始, 共计存10次,每年末应该等额存入( )元。(F/A,2%, 10)=10.95 A.8706.24 B.6697.11 C.8036.53 D.9132.42
『解答』
如果上例中通货膨胀率为4%,
【例题23· 单选题】一项600万元的借款,借款期3年,年利 率为10%,若每半年复利一次,则年实际利率为( ) A.10% B.5% C.10.25% D.10.75%
『正确答案』C 『答案解析』i=(1+r/m)m-1=(1+10%/2)2-1= 10.25%。
30000×(F/P,i,3)=50000 (F/P,i,3)=1.6667 当i=18%,则(F/P,18%,3)=1.643032 当i=19%,则(F/P,19%,3)=1.685159 解之得:i=18.55% 从以上计算可看出,徐先生目前的使用费3万元延期到3年后支付则需要5万元, 相当于年利率18.55%,远比银行贷款利率5%高,因此张先生3年后支付这 笔款项并不合算。
求出结果: i=8.36%
【例20】张先生要在一个街道十字路口开办一个餐馆,于是找 到十字路口的一家小卖部,提出要求承租该小卖部3年。小卖部 的业主徐先生因小卖部受到附近超市的影响,生意清淡,也愿意 清盘让张先生开餐馆,但提出应一次支付3年的使用费30000元。 张先生觉得现在一次拿30000元比较困难,因此请求能否缓期支 付。徐先生同意3年后支付,但金额为50000元。若银行的贷款 利率为5%,问张先生3年后付款是否合算?徐先生要求张先生不 是3年后一次支付,而是3年内每年年末支付12000元,那么张先 生是现在一次付清还是分3次付清更为合算?
【例题10】某投资项目于2012年年初动工,假设当年投产, 从投产之日起每年年末可得收益40000元。按年折现率6%计 算(复利计息),计算预期10年收益的现值。
『解答』 P=40000× =40000×(P/A,6%,10) =40000×7.3601 =294404(元)
【例题11】某公司打算购买一台设备,有两种付款方式:一是一 次性支付500万元,二是每年年初支付200万元,3年付讫。由于 资金不充裕,公司计划向银行借款用于支付设备款。假设银行借 款年利率为5%,复利计息。请问公司应采用哪种付款方式?
【例题13】某公司拟购置一处房产,房主提出两种付款方案: (1)从现在起,每年年初支付200万元,连续付10次,共2000 万元。 (2)从第5年开始,每年年初支付250万元,连续支付10次, 共2500万元。 假设该公司的资本成本率(即最低报酬率)为10%。 要求:通过计算现值回答,你认为该公司应选择哪个方案?
【例题15】某人拟在5年后还清10000元债务,从现在起每 年年末等额存入银行一笔款项。假设银行存款年利率为10%,
则每年需存入多少元?
『解答』根据公式A=F×(A/F,10%,5) =F/(F/A,10%,5) =10000/6.1051
=1637.97(元)
【例题16】某企业借得1000万元的贷款,在10年内
『解答』P=F/(1+i)n=100/(1+2%)5 =100×(P/F,2%,5) =100×0.9057
=90.57(元)
【例题5· 单选题】2011年1月1日,A公司租用一层写字楼作 为办公场所,租赁期限为3年,每年1月1日支付租通年金 B.预付年金 C.递延年金 D.永续年金
【例题20】吴先生存入1000000元,奖励每年高考的文理科 状元各10000元,奖学金每年发放一次。问银行存款年利率
(复利计息)为多少时才可以设定成永久性奖励基金?
『解答』由于每年都要拿出20000元,因此奖学金的性质是一 项永续年金,其现值应为1000000元,因此: i=20000/1000000=2% 也就是说,银行存款年利率不低于2%才能保证奖学金 的正常运行。
『正确答案』B
【例题6】小王是位热心于公众事业的人,自2005年12月 底开始,他每年都要向一位失学儿童捐款。小王向这位失学 儿童每年捐款1000元,帮助这位失学儿童从小学一年级读完 九年义务教育。假设每年定期存款利率都是2%(复利计息), 则小王9年的捐款在2013年年底相当于多少钱?
『解答』F=1000×(F/A,2%,9) =1000×9.7546 =9754.6(元)
『正确答案』D 『答案解析』本题是已知终值求年金,即计算偿债基金。 A=100000/(F/A,2%,10)=100000/10.95=9132.42
(元)。
【例题18· 单选题】在下列各项资金时间价值系数中,与资 本回收系数互为倒数关系的是( )。 A.(P/F,i,n)B.(P/A,i,n) C.(F/P,i,n)D.(F/A,i,n)
(元)
【例题3】某人将100元存入银行,复利年利率2%,求5年后 的终值。
『解答』F=P×(1+i)n=100×(1+2%)5 =100×(F/P,2%,5) =100×1.1041 =110.41(元)
【例题4】某人为了5年后能从银行取出100元,在复利年利 率2%的情况下,求当前应存入的金额。
『解答』甲公司的投标书显示,如果该公司取得开采权,从获得开采权的 第1年开始,每年年末向A公司交纳10亿美元的开采费,直到10年后开 采结束。 F=A×(F/A,i,n)=10×(F/A,15%,10) =10×20.304 =203.04(亿美元) F=40×(F/P,15%,10) +60×(F/P,15%,2) = 40×4.0456 +60×1.3225 =241.174(亿美元) 甲公司付出的款项终值小于乙公司付出的款项的终值,因此,A公司应接 受乙公司的投标
【例题8】为给儿子上大学准备资金,王先生连续6年于 每年年初存入银行3000元。若银行存款利率为5%,则王先生
在第6年末能一次取出本利和多少钱?
『解答』F=A[(F/A,i,n+1)-1] =3000×[(F/A,5%,7)-1] =3000×(8.1420-1) =21426(元) F=A×(F/A,i,n)×(1+i) =3000×(F/A,5%,6)×(1+5%) =3000×6.8019×1.05 =21426(元)
