二分类与多分类Logistic回归模型
Logistic 回归模型

• 反对数变换得到 OR e1
11
实例1
研究急性心肌梗塞(AMI)患病与饮酒 的关系, 采用横断面调查。
饮酒 不饮酒 合计
(X=1) (X=0)
患病(y=1) 55 74 129
未患病(y=0) 104663 212555 317218
合计
104718 21262Odds分别为
O R e1e1 .7 9 1 7 5 96
95% CI=(4.3, 8.5)
34
实例3:Logistic模型的交互作用
• 由于本例模型为
L o g i t( P ) 0 1 x 1 2 x 2 3 x 1 x 2
• 3,P=,差别有统计学意义,可以认为吸烟 和家属史对患肺癌有交互作用。
33
实例3:Logistic模型的交互作用
• 由于本例模型为 L o g i t( P ) 0 1 x 1 2 x 2 3 x 1 x 2
• 对于无家属史,x2=0代入模型,得到
Logit(P)01x1
• 由回归系数与OR的关系,得到吸烟的:
2
数据分析的背景
• 单因素的分类资料统计分析,一般采用 Pearson 2进行统计检验,用Odds Ratio 及其95%可信区间评价关联程度。
• 考虑多因素的影响,对于反应变量为分 类变量时,用线性回归模型P=a+bx就不 合适了,应选用Logistic回归模型进行统 计分析。
3
Logistic回归模型
• 在本例中,对于同为吸烟或不吸烟的对象 而言(x2相对固定不变),
• 饮酒(x1=1)的对数Odds为
L o g (O d d s x 1 1 )0 1 2 x 2
• 不饮酒(x1=0)的对数Odds为
Logistic回归

不同体质指数高血压患病率
BMI(X) 调查人数
患病 (y=1) 1331
1656 2987
未患病 (y=0) 5461
2492 7953
患病率 (%) 19.60
39.92 27.30
正常(x=0)
超重(x=1) 合计
6792
4148 10940
Logistic回归模型为:
模型中回归系数的解释: X=1时(超重): X=0时(正常):
1.
2.当自变量为连续型变量时,不需编码
表示自变量X每增加一个单位得到的比值比的自然对数 例如:前列腺癌患者淋巴组织有无转移与年龄(X)回归模 型
实际工作中,常把连续型变量→等级资料来解释。
3. 当自变量为有序分类变量时,一般按等级对疾病 影响的顺序由大到小编码。(各等级对应变量的 影响是线性变化的)
无序多分类Logistic模型
例: 研究不同细胞分化程度(X1)和细胞染色 (X2)与恶性肿瘤组织类型(Y)的关系, 得到资料如表,分析细胞分化程度和细胞 染色与组织类型的关系。
得到两个回归方程:
以大细胞癌水平3为基准,分别用两个回归进行 水平1与水平3、水平2与水平3的比较。
X1的系数均为正值,说明分化程度高,鳞 癌和腺癌的危险高于大细胞癌的危险 X2的系数均为负值,说明细胞染色阳性, 鳞癌和腺癌的危险高于大细胞癌的危险
0
1 1 … 0
建立模型:
P(一对中只有一人得病)=P(A得病)P(B不得病)+ P(A不得病)P(B得病) 在病例和对照中只有1人得病的条件下恰好是A得病的条件概 率为 P(A得病|一对中只有一人得病)= P(A得病)P(B不得病) P(A得病)P(B不得病)+ P(A不得病)P(B得病)
Logistic回归分析

• Wald检验( wald test)
即广义的t检验,统计量为u
u= bi s bi
u服从正态分布,即为标准正态离差。
Logistic回归系数的区间估计
bi u Sbi
第十八页,共52页。
上述三种方法中,似然比检验最可靠, 比分检验一般与它相一致,但两者均要求较 大的计算量;而Wald检验未考虑各因素间 的综合作用,在因素间有共线性时结果不如 其它两者可靠。
Odds=P/(1-P)
比数比
OR=[P1/(1-P1)]/[P2/(1-P2)]
在患病率较小情况下,OR≈RR
第二十二页,共52页。
设P表示暴露因素X时个体发病的概率, 则发病的概率P与未发病的概率1-P 之比 为优势(odds), logit P就是odds的对数
值。
• 优势比 • 常把出现某种结果的概率与不出现的概率之
P=1 Logit(P)=Ln(1/0)=+无穷大
Logit(P )取值范围扩展为(-,+ -)
第十页,共52页。
• Logit变换
也称对数单位转换
logit P=
ln
P 1 P
第十一页,
P 1e e( 1x12x2 nxn ) 1
1 P 1 e( 1x12x2 nxn )
• 分析因素xi为连续性变量时, e(bi)表示xi增加 一个计量单位时的优势比。
第二十七页,共52页。
多因素Logistic回归分析时,对回归系
数的解释都是指在其它所有自变量固定的情 况下的优势比。存在因素间交互作用时,
Logistic回归系数的解释变得更为复杂,应
特别小心。
第二十八页,共52页。
其中,为常数项,为偏回归系数。
多层次logistic回归模型

多层次logistic回归模型英文回答:Logistic regression is a popular statistical model used for binary classification tasks. It is a type of generalized linear model that uses a logistic function to model the probability of a certain event occurring. The model is trained using a dataset with labeled examples, where each example consists of a set of input features and a corresponding binary label.The logistic regression model consists of multiple layers, each containing a set of weights and biases. These weights and biases are learned during the training process, where the model adjusts them to minimize the difference between the predicted probabilities and the true labels. The layers can be thought of as a hierarchy of features, where each layer learns to represent more complex and abstract features based on the input features from the previous layer.In the context of deep learning, logistic regression can be extended to have multiple hidden layers, resulting in a multi-layer logistic regression model. Each hidden layer introduces additional non-linear transformations to the input features, allowing the model to learn more complex representations. This makes the model more powerful and capable of capturing intricate patterns in the data.To train a multi-layer logistic regression model, we typically use a technique called backpropagation. This involves computing the gradient of the loss function with respect to the model parameters and updating the parameters using gradient descent. The backpropagation algorithm efficiently calculates these gradients by propagating the errors from the output layer back to the input layer.Multi-layer logistic regression models have been successfully applied to various domains, such as image classification, natural language processing, and speech recognition. For example, in image classification, a multi-layer logistic regression model can learn to recognizedifferent objects in images by extracting hierarchical features from the pixel values.中文回答:多层次logistic回归模型是一种常用的用于二分类任务的统计模型。
logistic回归模型——方法与应用

logistic回归模型——方法与应用
logistic回归模型是一种广泛应用于分类问题的统计学习方法。
它主要用于预测二分类问题,但也可以通过多类logistic回归
处理多分类问题。
方法:
1. 模型定义:logistic回归模型是一种线性分类模型,它
使用一个Logistic函数(也称为sigmoid函数)将线性模型生成
的线性组合转换为概率分数。
Logistic函数将线性组合映射到
0到1之间的值,表示输入属于正面类别的概率。
2. 模型训练:logistic回归模型的训练目标是找到一个权
重向量,使得模型能够最大化正面类别的概率。
训练算法通常采用最大似然估计方法,通过迭代优化权重向量来最小化负对数似然损失函数。
3. 预测:给定一个测试样本,logistic回归模型通过计算
样本的得分(也称为Logit),将其映射到0到1之间的概率分数。
如果概率分数超过一个预先定义的阈值,则将测试样本分类为正面类别,否则将其分类为负面类别。
应用:
1. 二分类问题:logistic回归模型最常用于解决二分类问题,例如垃圾邮件过滤、欺诈检测等。
2. 多类问题:通过多类logistic回归模型,可以将多个类别映射到0到1之间的概率分数,然后根据概率分数将测试样本分配到不同的类别中。
3. 特征选择:logistic回归模型可以用于特征选择,通过计算每个特征的卡方得分,选择与类别最相关的特征。
4. 文本分类:logistic回归模型在文本分类问题中得到广泛应用,例如情感分析、主题分类等。
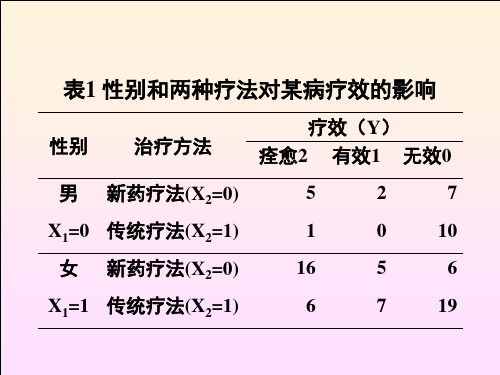
B2有序多分类Logistic回归模型
似然比检验:模型中自变量偏回归系 数是否全为0。结果P=0.000,说明至 少有一个自变量的偏回归系数不为0。
Model Fitting Inform ation
Model Intercept Only
-2 Log Likelihood
43.484
Final
23.598
Link function: Logit.
95% Conf idence Interval
Low er Bound Upper Bound
-.175
1.163
.621
2.076
.871
2.724
.
.
-2.356
-.282
.
.
• OR=exp()
• 不同疗法的OR值为exp(1.797)=6.03。新疗
法优于传统疗法。疗效至少优于1个等级 的可能性,新疗法是传统疗法的6.03倍。
a. Link f unction: Logit.
参数估计
• 无效,有效,治愈无效与有效治愈,无
效有效与治愈,可建立两个方程。
ln
1
无无效效的的概概率率
0.494
(1.797treat
1.319sex )
ln
1
无无效效和和有有效效的的概概率率
1.348
(1.797treat
1.319sex )
Tes t of Parallel Linesa
Model
-2 Log
Likelihood Chi-Square
df
Sig.
Null Hy pothesis
23.598
General
22.128
1.469
logistic回归

l o g i s t i c回归-CAL-FENGHAI.-(YICAI)-Company One1定性资料的回归分析------Logistic 回归Logistic 模型的主要用途:1. 用作影响因素分析2.作为判别分析方法 第一节 二分类变量的logistic 回归逻辑回归区别于线性回归,最主要的特点就一个:它的因变量是0-1型数据。
啥是0-1型数据?就是这个数据有且仅有两个可能的取值。
数学上为了方便,把其中一个记作0,另外一个记作1.例1:购买决定:我是买呢还是买呢还是买呢如果您的决策永远是:买、买、买,这不是0-1数据。
我们说的购买决策是:买还是不买定义:1=购买,0=不购买。
这个关于购买决定的0-1变量老牛了。
为啥?因为它支撑了太多的重要应用。
例如,我生产了一瓶矿泉水,叫做“农妇山泉有点咸”,到底卖给谁呢为此,我们需要做市场定位。
什么是市场定位市场定位从回归分析的角度看,就是想知道:谁会买这个产品谁不会买或者说:谁购买这个产品的可能性大,谁购买的可能性小。
这样我们就可以瞄准可能性最高的一批人,他们就构成了我的目标市场。
这就是我们通常所说的市场定位。
令Y 表示购买决定,那么影响它的因素有很多。
比如,消费者自己的人口特征1X 、消费者过去的购买记录是2X 、来自社交网络朋友的行为信息3X 、产品自己的特征4X 、产品正在承受的市场手段策略(例如:促销)5X 、竞争对手的市场动作6X 等等。
一.模型建立 理论回归模型:01122ln...,1p p px x x pββββ=+++-其中1(1,...,)p p p y x x ==。
注:1pp- 称为优势(odds), 表示某个事件的相对危险度. 获得容量为n 的样本()12,,,,1,...,i i ip i x x x y i n =后可得样本回归模型:01122ln,1ii i p ip ip x x x p ββββ=+++-其中1(1,...,)i i p p p y x x ==,1,...,i n =。
十三、logistic回归模型

非条件logistic回归
模型简介
❖
简单分析实例
内
容
哑变量设置
提
自变量的筛选方法与逐步回归
要
模型拟合效果与拟合优度检验
模型的诊断与修正
条件logistic回归
模型简介
对分类变量的分析,当考察的影响因素较少,且也为分类 变量时,常用列联表(Contingency Table)进行整理,并 用2检验或分层2检验进行分析,但存在以下局限性:
.184
Wal d 6.391
30.370 6.683 4.270
33.224
df 1 1 1 1
1
Sctep lwt
3
ptl
-.015
.007
5.584
1
.728
.327
4.961
1
ht
1.789
.694
6.639
1
Constant
.893
.829
1.158
1
a. Variable(s) entered on step 1: ptl.
模型拟合效果检验
结果分析
Area Under the Curv e
Test Result Variable(s): Predicted probability
Area Std. Errora
.708
.043
Asymptotic Sigb. .000
Asymptotic 95% Confidence Interval
❖ 给出了模型拟合过程中每一步的-2log(L)及 两个伪决定系数。
逐步回归
结果分析
Variables in the Equation
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二分类Logistic 回归模型在对资料进行统计分析时常遇到反应变量为分类变量的资料,那么,能否用类似于线性回归的模型来对这种资料进行分析呢?答案是肯定的。
本章将向大家介绍对二分类因变量进行回归建模的Logistic 回归模型。
第一节 模型简介一、模型入门在很多场合下都能碰到反应变量为二分类的资料,如考察公司中总裁级的领导层中是否有女性职员、某一天是否下雨、某病患者结局是否痊愈、调查对象是否为某商品的潜在消费者等。
对于分类资料的分析,相信大家并不陌生,当要考察的影响因素较少,且也为分类变量时,分析者常用列联表(contingency T able)的形式对这种资料进行整理,并使用2χ检验来进行分析,汉存在分类的混杂因素时,还可应用Mantel-Haenszel 2χ检验进行统计学检验,这种方法可以很好地控制混杂因素的影响。
但是这种经典分析方法也存在局限性,首先,它虽然可以控制若干个因素的作用,但无法描述其作用大小及方向,更不能考察各因素间是否存在交互任用;其次,该方法对样本含量的要求较大,当控制的分层因素较多时,单元格被划分的越来越细,列联表的格子中频数可能很小甚至为0,将导致检验结果的不可靠。
最后,2χ检验无法对连续性自变量的影响进行分析,而这将大大限制其应用范围,无疑是其致使的缺陷。
那么,能否建立类似于线性回归的模型,对这种数据加以分析?以最简单的二分类因变量为例来加以探讨,为了讨论方便,常定义出现阳性结果时反应变量取值为1,反之则取值为0 。
例如当领导层有女性职员、下雨、痊愈时反应变量1y =,而没有女性职员、未下雨、未痊愈时反应变量0y =。
记出现阳性结果的频率为反应变量(1)P y =。
首先,回顾一下标准的线性回归模型:µ11m mY x x αββ=+++L 如果对分类变量直接拟合,则实质上拟合的是发生概率,参照前面线性回归方程 ,很自然地会想到是否可以建立下面形式的回归模型:µ11m mP x x αββ=+++L 显然,该模型可以描述当各自变量变化时,因变量的发生概率会怎样变化,可以满足分析的基本要求。
实际上,统计学家们最早也在朝这一方向努力,并考虑到最小二乘法拟合时遇到的各种问题,对计算方法进行了改进,最终提出了加权最小二乘法来对该模型进行拟合,至今这种分析思路还偶有应用。
既然可以使用加权最小二乘法对模型加以估计,为什么现在又放弃了这种做法呢?原因在于有以下两个问题是这种分析思路所无法解决的:(1)取值区间:上述模型右侧的取值范围,或者说应用上述模型进行预报的范围为整 个实数集(,)-∞+∞,而模型的左边的取值范围为01P ≤≤,二者并不相符。
模型本身不能保证在自变量的各种组合下,因变量的估计值仍限制在0~1内,因此可能分析者会得到这种荒唐的结论:男性、30岁、病情较轻的患者被治愈的概率是300%!研究者当然可以将此结果等价于100%可以治愈,但是从数理统计的角度讲,这种模型显然是极不严谨的。
(2)曲线关联:根据大量的观察,反应变量P 与自变量的关系通常不是直线关系,而是S 型曲线关系。
这里以收入水平和购车概率的关系来加以说明,当收入非常低时,收入的增加对购买概率影响很小;但是在收入达到某一阈值时,购买概率会随着收入的增加而迅速增加;在购买概率达到一定水平,绝大部分在该收入水平的人都会购车时,收入增加的影响又会逐渐减弱。
如果用图形来表示,则如图1所示。
显然,线性关联是线性回归中至关重要的一个前提假设,而在上述模型中这一假设是明显无法满足的。
图1 S 型曲线图以上问题促使统计学家们不得不寻求新的解决思路,如同在曲线回归中,往往采用变量变换,使得曲线直线化,然后再进行直线回归方程的拟合。
那么,能否考虑对所预测的因变量加以变换,以使得以上矛盾得以解决?基于这一思想,又有一大批统计学家在寻找合适的变换函数。
终于,在1970年,Cox 引入了以前用于人口学领域的Logit 变换(Logit Transformation),成功地解决了上述问题。
那么,什么是Logit 变换呢?通常的把出现某种结果的概率与不出现的概率之比称为比值(odds ,国内也译为优势、比数),即1Odds ππ=-,取其对数ln()ln 1Odds πλπ==-。
这就是logit 变换。
下面来看一下该变换是如何解决上述两个问题的,首先是因变量取值区间的变化,概率是以0.5为对称点,分布在0~1的范围内的,而相应的logit(P)的大小为:0π= logit()ln(0/1)π==-∞0.5π= logit()ln(0.5/0.5)0π==1π= logit()ln(1/0)π==+∞显然,通过变换,Logit(π)的取值范围就被扩展为以0为对称点的整个实数域,这使得在任何自变量取值下,对π值的预测均有实际意义。
其次,大量实践证明,Logit(π)往往和自变量呈线性关系,换言之,概率和自变量间关系的S 形曲线往往就符合logit 函数关系,从而可以通过该变换将曲线直线化。
因此,只需要以Logit(π)为因变量,建立包含p 个自变量的logistic 回归模型如下:011log it()p p P x x βββ=+++L以上即为logistic 回归模型。
由上式可推得:011011exp()1exp()p p p p x x P x x ββββββ+++=++++L L 011111exp()p p P x x βββ-=++++L 上面三个方程式相互等价。
通过大量的分析实践,发现logistic 回归模型可以很好地满足对分类数据的建模需求,因此目前它已经成为了分类因变量的标准建模方法。
通过上面的讨论,可以很容易地理解二分类logistic 回归模型对资料的要求是:(1)反应变量为二分类的分类变量或是某事件的发生率。
(2)自变量与Logit(π)之间为线性关系。
(3)残差合计为0,且服从二项分布。
(4)各观测值间相互独立。
由于因变量为二分类,所以logistic 回归模型的误差应当服从二项分布,而不是正态分布。
因此,该模型实际上不应当使用以前的最小二乘法进行参数估计,上次均使用最大似然法来解决方程的估计和检验问题。
二、一些基本概念由于使用了logit 变换,Logistic 模型中的参数含义略显复杂,但有很好的实用价值,为此现对一些基本概念加以解释。
1. 优势比如前所述,人们常把出现某种结果的概率与不出现的概率之比称为比值(odds ),即1P odds P=-。
两个比值之比称为优势比(odds Ratio ,简称OR )。
首先考察OR 的特性:若12P P >,则12121211P P odds odds P P =>=-- 若12P P <,则12121211P P odds odds P P =<=-- 若12P P =,则12121211P P odds odds P P ===-- 显然,OR 是否大于1可以用作两种情形下发生概率大小的比较。
2. Logistic 回归系数的意义从数学上讲,β和多元回归中系数的解释并无不同,代表x 改变一个单位时logit(P )的平均改变量,但由于odds 的自然对数即为logit 变换,因此Logistic 回归模型中的系数和OR 有着直接的变换关系,使得Logistic 回归系数有更加贴近实际的解释,从而也使得该模型得到了广泛的应用。
下面用一个实例加以说明:以4格表资料为例具体说明各回归系数的意义:表1 4格表资料治疗方法(treat)治疗结果(outcome ) 合计 治愈率治愈(=1) 未治愈(=0) 新疗法(=1)60 (a) 21 (c) 81 74.07% 传统疗法(=0)42 (b) 27 (d) 69 60.87% 合计102 48 130 68.00%该资料如果拟合Logistic 回归模型,则结果如下(操作步骤详见后述):01(|1)0.4420.608Logit P outcome treat treat ββ==+⨯=-+⨯(1)常数项:表示自变量取全为0(称基线状态)时,比数(Y=1与Y=0的概率之比)的自然对数值,本例中为00.442ln[(42/69)/(27/69)]ln(42/27)ln(/)b d β=-===,即传统疗法组的治愈率与未治愈率之比的自然对数值。
在不同的研究设计中,常数项的具体含义可能不同,如基线状态下个体患病率、基线个体发病率、基线状态中病例所占比例等,但这些数值的大小研究者一般并不关心。
(2)各自变最的回归系数:i β(1,)i p =L 表示自变量i x 每改变一个单位,优势比的自然对数值改变量,而exp()i β即OR 值,表示自变量i x 每变化一个单位,阳性结果出现概率与不出现概率的比值是变化前的相应比值的倍数,即优势比(注意:不是出现阳性结果的概率为变化前的倍数,即优势比并不等同于相对危险度)。
本例中自变量治疗方法的回归系数10.608β=,为两组病人的治愈率与未治愈率之比的对数值之差,即ln[(60/81)/(21/81)]ln[(42/69)/(27/69)]ln(/)ad bc ==。
因此,对于四格表资料而言,所建立的Logistic 回归模型也可以写成:logit(|1)ln(/)ln(/)ln(/)ln()P outcome b d ad bc treat b d OR treat ==+⨯=+⨯ 由以上关系可知,0exp()β表示传统疗法组的治愈率与未治愈之比值。
1exp()β则表示治疗方法增加一个单位,即将疗法从传统疗法改为新疗法时,新疗法组病人治愈率与未治愈率之比值相对于传统疗法组病人的治愈率与未治愈率比值的倍数。
而两组病人的治愈率之比(60/81)/(42/69) 1.217==,并不完全相同。
但是,当研究结果出现阳性的概率较小时(一般认为小于0.1 ,反之当概率大于0.9时亦可),OR 值大小和发生概率之比非常接近,此时可以近似地说一组研究对象的阳性结果发生率是另一组研究对象发生率的OR 值倍,即用OR 值的大小来挖地表示相对危险度的大小。
三、简单分析实例SPSS中通过regression模块中的Binary Logistic过程实现结果变量为二分类的Logistic回归,下面通过一个实例分析,具体讲解相应的操作和结果解释。
例1某医师希望研究病人的年龄(岁)、性别(0为女性,1为男性)、心电图检验是否异常(ST段压低,0为正常、1为轻度异常、2为重度异常)与患冠心病是否有关。
调用SPSS中的Binary Logistic过程:图2 Logistic回归主对话框本例中涉及的对话框界面如图9.2所示,注意对话框中部有一个以前未出现过的a*b 按钮、用于纳入交互作用,只要先将相应变量选中,然后单击此按钮,相应的交互项就会被纳入模型。
