自动控制理论之频率域稳定判据及稳定裕度探讨.详解
《自动控制原理》 胡寿松 5-3 频域稳定判据 频域稳定判据

面可以找到相应的象。
在s平面上任选一条闭合曲线Г,且不通过F(s)的
任一零点和极点,s从闭合曲线Г上任一点A起,顺时
针沿Г运动一周回到A点,则通过F(s) 映射,在F(s)
平面上也从点F(A)起,到点F(A)止亦形成一条闭合
曲线ГF ,如下图所示。
下面,研究s在[s]平面上沿封闭曲线Γ顺时针 运动一周,ΓF包围坐标原点的次数和运动方向, 即F(s)的相角变化情况。
lim
1
0
A(0 ) | G ( j 0 ) H ( j 0 ) |
e
j [ ( 90 )]
G1 ( j 0) e
jG1 ( j 0 )
e
j [ ( 90 ) G1 ( j 0 )]
(0 ) G ( j 0 ) H ( j 0 ) (90 ) G1 ( j 0)
F ( s) 1 G( s) H ( s)
K ( s zi )
i 1
n
(s p )
i i 1
n
F ( s) ( s z1 ) (s z2 ) ( s zn ) (s p1 ) (s p2 ) ( s pn )
F ( s) ( s z1 ) ( s z2 ) ( s zn ) ( s p1 ) ( s p2 ) ( s pn )
由于z1, p1被闭合曲线Γ包围,当复变量s沿闭合
曲线Γ顺时针运动一周时,显然复向量s-z1, s-p1的相
当开环系统有积分环节时
1 设 G(s) H (s) G1 (s) ( 0, | G1 ( j 0) |) s
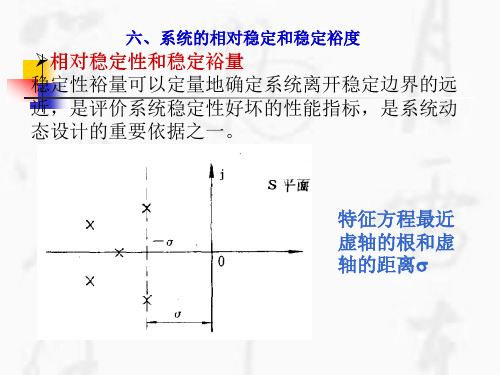
自动控制原理-5-4频域稳定裕度

最小相位系统中,即开环不稳定极点数P =0,奈氏曲线离(-1,j0)点越远,其相对稳 定性越好;反之,相对稳定性越差。
若奈氏曲线 穿过(-1,j0)点,则系统处于临界稳定状态。
在频率特性中用相位裕量和幅值裕量两个性能指标来衡量最小相位系统的相对稳定性。
5-4 频域稳定裕度1、相位裕度 g定义:曲线上,模值为1的矢量和负实轴间的夹角。
) ( 180 c w j g + = o 截止频率 0 < g ,曲线包围(1,j0)点,闭环系统不稳定。
, 0 > g 闭环系统稳定。
g 越大,系统相对稳定性越好,一般取30°~60°。
1 - c w x w ) ( c w j )(x A w g c w x w ) (w j )(w L p - ww) ( x w j gh2、幅值裕量 h1 < h ,闭环系统不稳定。
, 1 > h 闭环系统稳定。
h>1时,h 越大,系统相对稳定性越好。
定义: 的倒数。
时, ) ( ) ( 180 ) ( x x x j H j G w w w j ° - = ) ( 1) ( ) ( 1 x x x A j H j G h w w w = = )( ) ( ) ( lg 20 ) ( dB j H j G dB h x x w w - = h(dB):对数幅值稳定裕度 1 - c w x w ) ( c w j )(x A w g c w x w ) (w j )(w L p - ww) ( x w j gh当 时,即 和 时,闭环系统是稳 定的;否则是不稳定的。
对于最小相位系统, 和 是同时发生或同时不发生的,所以经常只 用一种稳定裕度来表示系统的稳定裕度。
常用相角 裕度。
0 ) ( > dB h 1 ) ( < x A w 0 > g 0) ( > dB h 0 > g 1 - c w xw ) ( c w j ) ( x A w g c w x w ) (w j )(w L p - w w ) ( x w j gh比如,若增加开环放大系数K ,则对数幅频特性曲线将上升,而 相角特性曲线不变。
《自动控制原理》第5章 控制系统的频域分析 :稳定裕度

0.4
0.2
0
0
5
10
15
20
25
30
35
40
Time (sec)
一、根据开环对数频率特性分析系统性能 (三频段)
1、低频段分析系统的?
低频斜率 系统型别
0dB/dec
0
-20dB/dec
Ⅰ
-40dB/dec
Ⅱ
阶跃输入稳态误差
1 K 1
0 0
19
低频段分析系统的稳态性能
斜率决定系统的型,ess 低频段高度决定开环增益K
1 h
A( x )
-1
幅值裕度h 1
A(x )
9
L(ω) 最 小 相 位 系 统
Φ(ω)
90
-20dB/dec
h
h 20lg( A(x )) L(x )dB
不稳定
ω
h>0:系统是稳定的。
ω
180
270
10
例1: 已知系统开环传递函数为:
G(s)
s2 (s
200 2)(s
1)
求幅值裕度和相角裕度。
时域:动态过程的开始部分。
28
二、根据闭环对数频率特性分析系统性能 自学部分
29
本章学习重点
理解频率特性的定义 熟练掌握串联开环系统的频率特性极坐标图和 Bode图的绘制 熟练掌握Nyquist 稳定判据 掌握根据开环对数频率特性分析闭环系统的动 态性能和稳态性能。
30
时域:动态过程的中间部分。
高阶系统:经验公式
0.16 0.4( 1 1) 35 90 sin
ts
(4
~
9)
1
c
阅读:218页例5-16
自动控制理论之频率域稳定判据及稳定裕度探讨

Z P R P 2N
例5-7 系统开环传递函数为
K G( s) H ( s) (T1s 1)(T2 s 1)
其幅频特性图如图5-44左所示。试利用Nyquist判据判断闭 环系统的稳定性。
解 当三个参数取任何正值时,系统的两个开环极点都是 负实数,即S平面右半部分无开环极点,P=0。频率特性及 其镜像组成的封闭曲线如图5-44右所示。可见,当ω 从 -∞→+∞ 时,闭合曲线并未包围(-1,j0)点,故N= 0。因此闭环系统总是稳定的。我们也可以利用劳斯判据 进行判定。
RP
奈氏判据:若系统的开环不稳定,即开环传递函数
G(S)H(S)在右半平面上有极点,其个数为P,则闭环系统 稳定的充分必要条件是:在GH平面上的开环频率特性 曲线G(jω)H(jω)及其镜像当ω从-∞变化到+∞时,将以逆 时针的方向围绕(-1,j0)点P圈;若系统开环稳定,即 P=0,则闭环系统稳定的充要条件是:在GH平面上的开环 频率特性曲线及其镜像不包围(-1,j0)点。 利用奈氏判据判断闭环系统不稳定,还可求出该系统在 右半s平面上的极点的个数
图5-47 K>1 和 K<1的频率特性曲线
3、Nyquist判据在Ⅰ型和Ⅱ型系统中的应用
设系统开环传递函数为
G (s) H (s)
K ( i s 1) s (T j s 1)
v j 1 i 1 n v
m
为利用Nyquist判据分析Ⅰ型和Ⅱ型系统的稳定性,就需要 修改s平面上原点附近的Nyquist路径,使它不通过s=0的开 环极点又仍然能包围整个右半s平面。方法是增补一个以 原点为圆心、半径R′为无穷小的右半圆。如图5-48所示
R 2N 2( N N )
自动控制原理讲义A1频率特性稳定裕度与系统频率指标
一、系统的频域性能指标
谐振频率:r 相对谐振峰值: Mr
截止频率b:M(b )
M(0) 2
带宽: 0≤ω≤ω b对应的频率范围
零频幅值M0 M0 =M(ω)| ω=0=M(0)
K
( jn 1)
((
j)
2
2 k
2 k k ( j)
1)
G( j) n1
k 1
( j) ( jTi 1) ((j)2 Tj2 2 jTj ( j) 1)
开环 (g ) 180
Kg
| G(
1
jg )H (
jg ) |
K g (dB) 20 lg K g 20 lg | G( jg )H( jg ) |
K g 6dB
系统响 应速度
增益裕量 相位裕量
闭环系统 稳定性
增益裕量 相位裕量 伺服机构: 10-20分贝 40度以上 过程控制: 3-10分贝 20度以上
M ( jw) G( jw) 1 G( jw)
A(w)
1
1 A2 (w) 2A(w) cos (w)2
1
2
1 A(w)
cos
(w)
sin2 (w)
cos (wr ) cos (wc ) cos
Mr
M (wr )
1
sin (wr )
1
sin
开环频域指标与时域指标的关系
G( jw)
例2 系统开环传递函数为
G(s)H (s)
K
s(T1s 1)(T2s 1)
KT1T2 1 T1 T2
P()
K (T1 T2 )
1 2 (T12 T22 ) 4T12T22
Q()
K (1 2T1T2 )
自动控制理论之频率域稳定判据及稳定裕度探讨讲诉

图5-47绘出了K>1 和 K<1的两条闭合曲线,可见:
当K>1 时,曲线逆时针包围了(-1,j0)点1圈即R=1 闭环系统稳定;当K<1时,曲线未包围(-1,j0)点,即 R=0,闭环系统不稳定。
在本例中,K值大才能使系统稳定,K值小反而使闭环系 统不稳定,这是与常见的最小相位系统截然不同之处。
因此,我们可以看出,辅助函数具有如下特征:
1)辅助函数F(S)是闭环特征多项式与开环特征多项式 之比,故其零点和极点分别为闭环极点和开环极点。
2)因为开环传递函数分母多项式的阶次一般大于或等 于分子多项式的阶次,故F(S)零点、极点的个数相同,均 为n个。
3)F(S)与开环传递函数G(S)H(S)之间只差常量1。 F(S)=1+G(S)H(S)的几何意义为:F平面上的坐标原点就是 GH平面上的(-1,j0)点,如图5-42所示。
负实数,即S平面右半部分无开环极点,P=0。频率特性及
其镜像组成的封闭曲线如图5-44右所示。可见,当ω 从 -∞→+∞ 时,闭合曲线并未包围(-1,j0)点,故N= 0。因此闭环系统总是稳定的。我们也可以利用劳斯判据 进行判定。
例5-8 设系统开环传递函数为
5.2 G(s)H (s) (s 2)(s2 2s 5)
图5-45 例5-8系统的极坐标图及其镜像
例5-9 系统结构图如图5-46所示,试判断系统的稳定性并 讨论K值对闭环系统稳定性的影响。
图5-46 解:图示系统是一个开环不稳定系统,其开环传递函数在 S平面右半部分有一个极点P=1,频率特性曲线如图5- 47所示。当ω =0时,曲线从负实轴(-K,j0)出发;当 ω→∞时,曲线以-90°渐近角趋于坐标原点;当ω从-∞ 变化到+∞,频率特性(图中实线部分)及其镜像(虚线 部分)包围(-1,j0)点的圈数R与K值有关。
控制系统的频域分析_稳定性与裕量

如果kg 1 ,则: 20logkg 0,系统稳定。 如果kg 1 ,则: 20logkg 0,系统不稳定。
内蒙古工业大学 机械学院
第5章 控制系统频域分析
(3)Bode图上的幅值裕量和相位裕量
g
1 kg
Im
Im
c
( )
Re Re
0
0
( )
c
L( )
1 kg
( )
( )
( ) 0 kg 0
c
L( )
( ) 0
kg 0
c
0
( )
g
kg
0
( )
kg
g
00
( )
00
( )
内蒙古工业大学 机械学院
第5章 控制系统频域分析
例:已知系统的开环传递函数如下:
1000 (0.5s 1) G( s) H ( s) s(2s 1)(s 2 10s 100)
内蒙古工业大学 机械学院
第5章 控制系统频域分析
反馈控制系统
G1(s)
H(s)
A( s )C ( s ) G1 ( s ) H ( s ) 闭环传 B( s ) D( s ) 递函数 G1 ( s ) A( s ) D( s ) G( s) 1 G1 ( s ) H ( s ) A( s)C ( s ) B( s ) D( s ) A( s )C ( s ) B( s ) D( s ) F ( s ) 1 G1 ( s ) H ( s ) B( s) D( s )
内蒙古工业大学 机械学院
奈氏判据
Z=P-N; Z=0时稳定。
《自动控制原理》第5章 控制系统的频域分析:频域稳定判据
N+ = 0,
3
N−
=
, 2
R = −3
例1: 设闭环系统的开环传递函数为:
K H (s)G(s) =
(T1s + 1)(T2s + 1)
Nyquist Diagram 0.6
0.4
0.2
Imaginary Axis
0
-0.2
系统稳定 -0.4
-0.6
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
R 0顺时针 R = 0不包围 R 0逆时针
在[s]任取一条闭合曲线T,包围F(s)的Z个零点和P个 极点,且不通过F(s)的零点和极点,当复变量s沿曲 线T顺时针绕一周时,在[F],TF包围原点的圈数 R=P-Z
3
二、闭环极点与开环极点的关系
设系统的开环传函:G(s)H (s) = B(s) A(s)
s(s + 1)( s + 2)
G(s) =
0.5 K
s(s + 1)(0.5s + 1)
G( j ) =
0.5 K
(K 0)
j ( j + 1)( j0.5 + 1)
G(
j )
=
− 0.5K[1.5 2 + j(1 − 2 ( 2 + 1)(0.25 2
0.5 2 )]
(K + 1)
0)
= 2
R = 2( N + − N − )
R 0, 顺时针 R 0, 逆时针
9
N+ = 0, N− = 1, R = 2(N+ − N− ) = −2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图5-40 映射关系
式中,P和Z分别是被闭合曲线Γ 包围的特征方程函数F (s) 的极点数和零点数。它表明,当 s 平面上的试验点 s1 沿 闭合曲线Γ 顺时针方向绕行一圈时,F(s)平面上对应的闭 合曲线将按逆时针方向包围坐标原点(P-Z)圈。
幅角原理:设S平面上不通过F(S)任何零极点的某条封 闭曲线Γ ,它包围了F(S)在S平面的Z个零点和P个极点。 当S以顺时针方向沿封闭曲线Γ 移动一周时,则在F平面 上对应于封闭曲线Γ 的像Γ F 将以顺时针的方向围绕原点 旋转R圈。R与Z、P的关系为:
Z P R P 2N
例5-7 系统开环传递函数为
K G( s) H ( s) (T1s 1)(T2 s 1)
其幅频特性图如图5-44左所示。试利用Nyquist判据判断闭 环系统的稳定性。
解 当三个参数取任何正值时,系统的两个开环极点都是 负实数,即S平面右半部分无开环极点,P=0。频率特性及 其镜像组成的封闭曲线如图5-44右所示。可见,当ω 从 -∞→+∞ 时,闭合曲线并未包围(-1,j0)点,故N= 0。因此闭环系统总是稳定的。我们也可以利用劳斯判据 进行判定。
图5-44 开环频率特性曲线与它在F平面上的对应曲线
对于包含了整个右半s平面的Nyquist路径来说,Z和P 分别为闭环传递函数和开环传递函数在右半s平面上的极 点数,而R则存在两种提法:(1)F平面上Γ F曲线围绕原 点的圈数;(2)GH平面上极坐标频率特性曲线及其镜像 围绕(-1,j0)点的圈数。 利用幅角定理判断闭环系统的稳定性,则闭环系统稳 定的充要条件为F(S)函数在s平面右半部的零点数Z=0即
R 2N 2( N N )
见书P-196
2、Nyquist稳定判据
为了确定辅助函数F(S)位于右半s平面内的所有零点、极 点数,现将封闭曲线Γ 扩展为整个右平面。曲线Γ 由三段 所组成: (1)正虚轴s=jω :频率ω由0变到+∞; (2)半径为无限大的右半圆 S=Rejθ:R→∞,θ : (3)负虚轴s=jω :频率ω由-∞变到0。 这种包含了整个右半s平面的闭合曲线Γ 称为Nyquist轨 迹,如图5-43所示。
图5-42 F平面与GH平面的关系图
Nyquist轨迹及其映射
为将映射定理与控制系 统稳定性的分析联系起来, 适当选择s平面的封闭曲线Γ。 如图5-43所示,它是由整个 虚轴和半径为∞的右半圆组 成,试验点按顺时针方向移 动一圈,该闭合曲线称为 Nyquist轨迹。 Nyquist轨迹在F(s)平面上 的映射也是一条封闭曲线, 称为Nyquist曲线。
图5-47绘出了K>1 和 K<1的两条闭合曲线,可见:
当K>1 时,曲线逆时针包围了(-1,j0)点1圈即R=1 闭环系统稳定;当K<1时,曲线未包围(-1,j0)点,即 R=0,闭环系统不稳定。
在本例中,K值大才能使系统稳定,K值小反而使闭环系 统不稳定,这是与常见的最小相位系统截然不同之处。
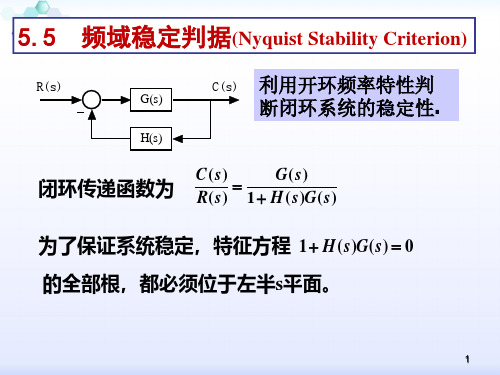
5-4 频率域稳定判据
控制系统的闭环稳定性是系统分析和设计所需解 决的首要问题,奈奎斯特稳定判据和对数频率稳定 判据是常用的两种频域稳定判据。频域稳定判据的 特点是根据开环系统频率特性曲线判定闭环系统的 稳定性,使用方便,易于推广。 Nyquist稳定判据既可以判断系统是否稳定(绝 对稳定性),也可以确定系统的稳定程度(相对稳 定性),还可以用于分析系统的瞬态性能以及指出 改善系统性能指标的途径。
例5-8 设系统开环传递函数为
5.2 G( s) H ( s) ( s 2)(s 2 2s 5)
试利用Nyquist判据判断闭环系统的稳定性。 解 绘出该系统的极坐标频率特性曲线如图5-45所示。 已知 P 0 由图知 R 2 ,则
Z P R 0 (2) 2
图5-45 例5-8系统的极坐标图及其镜像
例5-9 系统结构图如图5-46所示,试判断系统的稳定性并 讨论K值对闭环系统稳定性的影响。
图5-46
解:图示系统是一个开环不稳定系统,其开环传递函数在 S平面右半部分有一个极点P=1,频率特性曲线如图5- 47所示。当ω =0时,曲线从负实轴(-K,j0)出发;当 ω→∞时,曲线以-90°渐近角趋于坐标原点;当ω从-∞ 变化到+∞,频率特性(图中实线部分)及其镜像(虚线 部分)包围(-1,j0)点的圈数R与K值有关。
则
B(S)+A(S)和A(S)分别为闭环和开环的特征多项式。引入 辅助函数
B( s) A( s) B( s) F ( s) 1 G( s) H ( s) 1 A( s) A( s)
( s z1 )(s z2 ) ( s zn ) F ( s) ( s p1 )(s p2 ) ( s pn )
R PZ
R<0和R>0分别表示ΓF顺时针包围和逆时针包围F(s)平面 的原点,R=0表示不包围F(S)平面的原点。
(2)、复变函数F(S)的选择
图5-41 控制系统结构图 如图5-41所示结构图,其开环传递函数为
B( s) G( s) H ( s) A( s) G( s) G( s) B( s) ( s) 1 G ( s) H ( s ) 1 B( s) A( s) B( s)H ( s) A( s)
图5-43 s平面上的 Nyquist轨迹
Nyquist轨迹Γ由两部分组 成,一部分沿虚轴由下而上 移动,试验点s=jω在整个虚 轴上的移动,在F 平面上的 映射就是曲线F(jω) (ω由- ∞→+∞),如图5-44所示。 F(jω)=1+G(jω)H(jω)
Nyquist轨迹Γ的另一部分 为s平面上半径为∞的右半圆, 映射到F 平面上为 图5-44 F 平面上的 F (∞)=1+G (∞)H (∞) Nyquist曲线
例:分析下图映射关系
(3)、S平面闭合曲线Γ的选择 系统的闭环稳定性取决于系统闭环传递函数F(S)零 点的位置,因此当选择S平面闭合曲线Γ 包围S平面的右半 部分时,Z=0系统稳定。考虑到闭合曲线不通过F(S)任一 零极点的条件, Γ可取两种形式。见P194 (4)、G(S)H(S)曲线的绘制 已知S平面闭合曲线Γ关于实轴对称,故闭合曲线ΓGH也 关于实轴对称,因此只需画出正虚轴部分的曲线,得GH 的半闭合曲线,仍计为ΓGH。
图5-47 K>1 和 K<1的频率特性曲线
3、Nyquist判据在Ⅰ型和Ⅱ型系统中的应用
设系统开环传递函数为
G (s) H (s)
K ( i s 1) s (T j s 1)
v j 1 i 1 n v
m
为利用Nyquist判据分析Ⅰ型和Ⅱ型系统的稳定性,就需要 修改s平面上原点附近的Nyquist路径,使它不通过s=0的开 环极点又仍然能包围整个右半s平面。方法是增补一个以 原点为圆心、半径R′为无穷小的右半圆。如图5-48所示
所以按Nyquist判据判断该系统是不稳定的,其闭环系 统在右半s平面上的极点数为2。
利用Nyquist判据我们还可以讨论开环传递系数K对闭 环系统稳定性的影响。当K值改变时,在任一频率下将引 起幅频特性成比例地变化,而相频特性不受影响。对图545,当频率ω=3时,曲线与负实轴正好相交在(-2,j0) 点,若传递系数K缩小一半,即由5.2降为2.6时,曲线恰 好通过(-1,j0)点,这是临界稳定状态;若K值进一步 缩小,当K<2.6时,频率特性将从(-1,j0)点的右边穿 过负实轴,整个频率特性曲线将不再包围(-1,j0)点, 这时闭环系统则是稳定的了。
1、奈氏判据的数学基础
复变函数理论中的幅角原理是奈氏判据的数学基础, 幅角原理用于控制系统稳定性的判定还需选择辅助函数和 闭合曲线。 (1)、幅角原理 设S为复数变量,F(S)为S的有理分式函数。对于S平面 上任意一点S,通过复变函数F(S)的映射关系,在F(S)平 面上可以确定关于S的象。在S平面上任选一条闭合曲线Γ 且不通过F(S)的任何零点与极点,S从闭合曲线Γ 上任一 一点A起,顺时针沿Γ 运动一周,再回到A点,那么相应 F(S)平面上也从点F(A)起,到F(A)点止形成一条闭合曲线 Γ F。若F(S)在S平面上指定区域内是非奇异的,则有如图 5-39所示的映射关系。
根据映射定理可得,s平面上的Nyquist轨迹在F平面上 的映射F(jω)(ω从-∞→+∞) 包围坐标原点的次数R为 R=P-Z 式中,Z——位于F (s)平面右半部分的零点数,即闭 环右极点个数; P——位于F(s)平面右半部分的极点数,即开环右极 点个数; R——Nyquist曲线包围坐标原点的次数。 闭环系统稳定的条件为系统的闭环极点均在 s 平面的 左半平面,即 Z=0 或 R=P。
RP
奈氏判据:若系统的开环不稳定,即开环传递函数
G(S)H(S)在右半平面上有极点,其个数为P,则闭环系统 稳定的充分必要条件是:在GH平面上的开环频率特性 曲线G(jω)H(jω)及其镜像当ω从-∞变化到+∞时,将以逆 时针的方向围绕(-1,j0)点P圈;若系统开环稳定,即 P=0,则闭环系统稳定的充要条件是:在GH平面上的开环 频率特性曲线及其镜像不包围(-1,j0)点。 利用奈氏判据判断闭环系统不稳定,还可求出该系统在 右半s平面上的极点的个数
辅助函数也可以表示成零极点的形式
因此,我们可以看出,辅助函数具有如下特征: 1)辅助函数F(S)是闭环特征多项式与开环特征多项式 之比,故其零点和极点分别为闭环极点和开环极点。
2)因为开环传递函数分母多项式的阶次一般大于或等 于分子多项式的阶次,故F(S)零点、极点的个数相同,均 为n个。
3)F(S)与开环传递函数G(S)H(S)之间只差常量1。 F(S)=1+G(S)H(S)的几何意义为:F平面上的坐标原点就是 GH平面上的(-1,j0)点,如图5-42所示。
2
2
设0型系统的传递函数为
