关于个人所得税起征点的数学模型
【精品】数学建模有关纳税的分析与计算

数学建模有关纳税的分析与计算西南交通大学第二届“新秀杯”数学建模竞赛2011年10月27日-11月3日题目: C (填写A、B或C题)西南交通大学教务处西南交通大学实验室及设备管理处西南交通大学数学建模创新实践基地工资薪金所得个人所得税计算方法的优化模型摘要本文研究的是关于工资薪金所得个人所得税计算方法的优化问题,主要运用了数学lingo软件,建立了数学优化模型,最后对模型作出分析、评价和改进。
对于问题一:本文根据速算扣除数的相关定义,再结合月工资的纳税计算方法,最后得出计算扣除数。
对于问题二:本文首先从实际情况出发,结合题目要求,在从分考虑修订前后的个人所得税的前提下,确定了该员工年总收入分为工资薪金与年终奖金的基本思路,随后,本文建立了数学优化模型,并利用lingo软件,对该模型进行了求解,得出最优解,即该员工的个人年终纳税的最合理纳税方案。
对于问题三:本文首先以第三问为基础,结合实际情况,综合考虑税率大小,建立了数学优化模型,本文将节假日费用和偶然所得费用归于月工资报税,年终奖金一万元单独报税,建立了数学优化模型,并利用lingo软件,对该模型进行了求解,得出最优解,最合理的报税方案即为总税额最小的方案。
关键词:个人所得税合理纳税数学优化模型 lingo数学软件§ 1问题的重述一背景介绍十一届全国人大常委会第二十一次会议30日表决通过关于修改个人所得税法的决定。
法律规定,工资、薪金所得,以每月收入额减除费用3500元后的余额为应纳税所得额;工资、薪金所得,适用超额累进税率,税率为3%至45%。
修改后的个税法将于2011年9月1日起施行。
因此我国公民在今年纳税时,要对纳税方案进行合理规划。
二要解决的问题1、问题一如何计算税率计算公式的速算扣除数?2、问题二某公司员工连续两年全年总收入5—7万元/年, 若采用修改前、后的个税法,他应如何报税,从而达到合理报税。
3、问题三若该公司将在节假日(五一、国庆)发放节日费500-2000元,以及单独发放年终奖励1万元,而该员工在某月有工资外偶尔所得7000元,则该员工又应如何报税?1§2问题的分析一相关知识的介绍个人所得税是调整征税机关与自然人(居民、非居民人)之间在个人所得税的征纳与管理过程中所发生的社会关系的法律规范的总称。
个人所得税优化分配模型数学建模

个人所得税优化分配模型数学建模2011年第四届新疆大学生数学建模竞赛我们参赛选择的题号是(从A/B/C/D中选择一项填写): C参赛队员:1. 徐辉(信息工程学院通信工程13-1班级联系电话)2. 冯榆斌(信息工程学院通信工程13-2班级联系电话)3. 陈浩(信息工程学院计算机科学与技术12-3班级联系电)日期:2011 年5月9日个人所得税收入分配优化模型摘要为了解决个人所得税收入分配方案,特建立月工资收入和年终一次性奖金关于最小纳税额的函数关系模型,以解决如下问题:问题一:要实现员工的月工资和年终奖金的优化分配,在月工资等额的前提下,通过对国家提供的每月工资纳税和年终奖金纳税方案的分析,得出只有当员工每月纳税额()f x 和年终奖金纳税额()f y 之和为最小时,才能最优分配,从而建立目标函数模型[1]:12i 1A 12()()Min f x f y ==+∑税要实现员工年薪在3~15万的优化分配,通过对模型用C 语言编程进行循环嵌套[2],得出最优分配方案,当年收入为10万元时,每月工资为月工资6333x =元,年终奖24004.0y =元,此时年纳税额最小为9419.4元。
当年收入为3万到15万时,工资分配方案利用C 语言编程搜索,得出结果,部分数据:()()年收入,月收入,年终奖金单位:元 ( 30000, 2000, 6000 ), (31000, 2083 , 6004), (32000, 2166, 6004) , (33000 , 2250, 6000 ) (97000,6083, 24004), (98000,6166, 24008), (99000,6250, 24000), (100000,6333,24004)(147000,7250,60000), (148000,7333,60004), (149000,7416,60008),(150000,7500,60000) 问题二:要实现该夫妇年收入为9万元时的最优还贷计划,经分析存在两种情况: 1)在纳税最少的前提下,交付住房抵押贷款,其每月上交的贷款额X (专指从工资中扣除的钱还贷),应满足5500X ≤(9万元年薪对应的最优月工资),此模型为:1224000(10.1)55000(1)n i nx n p +?-?≥+2)每月上交贷款5500X ≥时,此时已不是纳税最优分配,这样每月多还款,必定会缩短贷款年限,贷款的利息会降低,这时只有保证在其纳税额和上交贷款最少前提下,年份也越少越符合要求,建立还贷模型:j ()[20%12(6600)12375Pr (9000012)12]Min Z n Y Y X =??-+?+-+结合两种情况,分别给出约束条件,运用Matlab7.0和10Lingo 软件编程求解,通过对两种情况下的结果进行比较分析,可以得出该夫妇10年还清银行贷款,每月还款7145.0X =元,年终奖金y=240000元。
个税函数公式解析

个税函数公式解析
个税函数是用来计算个人应缴纳的所得税的数学模型。
根据国家不同
的税率政策和税务制度的规定,个税函数会有所不同。
以下是对个税函数
的解析。
个税函数的一般形式如下:
T=f(I)
其中,T表示应缴纳的个人所得税额,I表示个人的税前收入。
f是
一个函数,根据税率规定而定。
个税函数的具体形式与税率表和税收起征点有关。
在中国,个税函数
一般采用7级累进税率表。
根据国家税务总局规定,2024年中国的个税
税率如下:
根据这个税率表,我们可以计算出个税函数的具体形式。
首先,我们需要确定应纳税所得额(即I减去个人所得税起征点):TI=I-5000
然后,根据TI的取值,我们可以得到对应的个税函数形式:
T=TI*3%
根据以上个税函数的表达式,我们可以计算出应缴纳的个人所得税额。
个税函数的解析对于个人和企业计算所需缴纳的个税很有帮助,也可
以帮助个人做好财务规划和税务筹划。
理解个税函数的计算方式,可以帮
助个人合理安排收入和支出,同时也可以帮助企业合理制定薪酬政策和税
务策略。
关于个人所得税的数学建模论文

CPI 125
120
115
110
105
100
95 1994 1996 1998 2000 2002 2004 2006 2008 2010
利用以上数据,运用逐步回归法计算以上四个指标的权重大小,得到只考虑人均 GDP,人均收入和消费指数 CPI 通过 MATLAB 编程(程序见附录 2)。 然后通过只考虑这三个方面的因素得到以下关系式: y=-272.8755-1.1924*x1+1.5605*x2+6.8087*x4 通过 MATLAB 编程(程序见附录 3)。
个人所得税的改革包括对起征点和税率级次级距的调整。级次级距的设置不 仅直接影响纳税人税后可支配收入的多少,而且对调节个人收入差距具有重要作 用。级次级距的设置与边际税率有关,经分析起征点的增长率与人均在岗职工的 工资密切相关,建立起征点指数增长模型,将其应用为税级设置模型,通过边际 税率计算其对应的全月应纳税所得额。
响,直接反应是其对个人所得税收入的影响,因此我们主要考虑其对个税收入的 影响。个税收入主要由起征点,级次级距以及就业人数决定。通过利用灰色理论 预测个人所得税起征点,级次级距调整对财政收入的影响。
针对以上问题分别建立数学模型,并通过 MATLAB 进行求解,利用网络数据 对所得方案进行定量分析,验证其合理性。
们发现起征点与人均收入,人均 GDP,通货膨胀率以及居民消费价格指数 CPI 有 关,通过逐步回归法和曲线拟合得到人均收入,人均 GDP, CPI 对其影响较大; 得出人均收入,人均 GDP,CPI 的函数关系表达式。
问题二的分析: 个人所得税的改革包括对税率级次级距的调整。级次级距的设置不仅直接影
日期:2011 年 08 月 11 日
最新个税计算、倒推Excel公式(起征点5000)
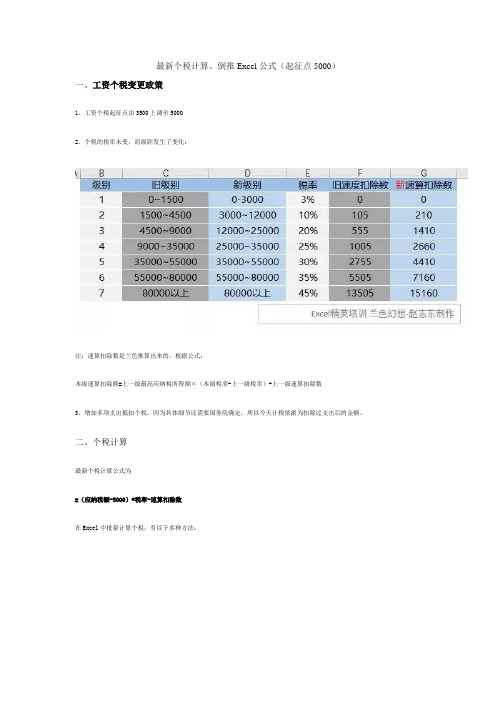
最新个税计算、倒推Excel公式(起征点5000)一、工资个税变更政策1、工资个税起征点由3500上调至50002、个税的税率未变,而级距发生了变化:注:速算扣除数是兰色推算出来的,根据公式:本级速算扣除额=上一级最高应纳税所得额×(本级税率-上一级税率)+上一级速算扣除数3、增加多项支出抵扣个税。
因为具体细节还需要国务院确定,所以今天计税依据为扣除过支出后的金额。
二、个税计算最新个税计算公式为=(应纳税额-5000)*税率-速算扣除数在Excel中批量计算个税,有以下多种方法:1、IF判断法公式太长,实在是没耐心写2、Vlookup函数法(C13单元格)=IFERROR((B13-5000)*VLOOKUP((B13-5000),C$3:E$9,2)-VLOOKUP((B13-5000),C$3:E$9,3),0) 3、Lookup函数法(D13单元格)=IFERROR((B13-5000)*LOOKUP(B13-5000,C$3:D$9)-LOOKUP(B13-5000,C$3:C$9,E$3:E$9),0) 4、Max函数法(E13单元格)推荐=5*MAX(0,B13*{0.6;2;4;5;6;7;9}%-{30;142;482;782;1182;1782;3482})5、Max数组公式法(F13单元格)=MAX(0,(B13-5000)*D$3:D$9-E$3:E$9)注:公式输入后按Ctrl+shift+enter三键输入,两边自动添加大括号后算成功{=MAX(0,(B13-5000)*D$3:D$9-E$3:E$9)}新个税可以省多少税?对比表来了,好象最开心的是霸道总....三、个税反推个税反推应纳税额,公式:F22单元格公式:=MIN((D22+{0;210;1410;2660;4410;7160;15160})/{0.03;0.1;0.2;0.25;0.3;0.35;0.45})+5000。
数学建模 所得税交纳点选址

B题:所得税交纳点选址所得税管理部门计划对某个地区中的所得税交纳点网络进行重新设计。
图B.1是对此地区内的城市和主要道路的示意图。
城市旁边的黑体数字表示城市的居民数目,单位为千人。
在连接城市之间的弧上标出了它们之间的距离,单位为千米(斜体字)。
为覆盖各个城市,所得税管理部门决定在三个城市中设置纳税点。
应在哪三个城市中设置纳税点才能够使居民与最近的纳税点之间平均距离最小?图B.1:此区域内的城市和道路图所得税交纳点选址摘要随着我国各地居民区的增加,及经济发展带来的高收入,纳税成为了国家财政收入的一大部分,税收作为国家经济杠杆之一,具有调节收入分配、促进资源配置、促进经济增长的作用。
纳税是国家财政收入的主要来源,国家用收来的税款发展经济、科技、教育、文化和国防等事业。
纳税点选址问题属于最佳选址问题,选址应用非常广泛,所得税缴纳点选址只是一个应用领域。
选址问题是一种长期决策,它的好坏直接影响到服务方式,质量,效率,成本。
能影响到利益与市场竞争力。
所以选址问题有着重大的经济社会意义。
选址问题研究的典型例如Weber问题,中值问题,覆盖问题,中心问题,多目标选址,竞争选址,不受欢迎的选址,选址-分配,选址-路线等。
随着选址理论的发展,很多种中心选址的方法被开发出来,归结起来主要可分为五种方法:解析方法,最优化线性方法,启发方法,仿真方法以及综合因素评价法,遗传算法,随即分析,模糊数学分析等等。
关键词:所得税缴纳点选址最短路径C++ 模型模型的符号说明符号符号说明G 赋权图G=(V,E)V 顶点集E 链接G各顶点的边集Hi 顶点Vi的权重D xy 链接顶点x和y的最短路径模型分析建立及求解1.模型预处理将各城市看成是图的结点,他们人口数量作为顶点的权重,链接它们的道路看成是图中的弧,则整个地区就可以抽象成一个无向的带权图G。
对给定一个无向带权图G=(V,E),其中V={V1,V2,….Vn}是非空顶点集,E={E1,E2,….En}是连接G各顶点的边集,Hi为顶点Vi的权重,G中的任何顶点a,b,D ab为代表连接a点和b点最短路径。
个人所得税5000起 征点正算及倒推反算公式模板(新版)
3、根据税后金额反推税前应发数
(填入C列,D列,F列公式自动计算) 公式下载此表后即可复制
税后实发金 额
三险一金合计
起征点
反算税前应发数(内设公 式)
核对(F列G列-C列=0 应缴税金 说明倒推公 式正确) 322.22 ######## -
10000 20000
-
5000 5000
10,322.22 21,987.50
30000 40000
-
5000 5000
34,786.67 48,700.00
######## ########
-
2、正算公式模板
(填入C列,D列,F列公式自动计算) 公式下载此表后即可复制 税前应发数 10000 20000 30000 40000 50000 三险一金合计 起征点 5000 5000 5000 5000 5000 应扣个税(内设公式) 290.00 1,590.00 3,590.00 6,090.00 9,090.00
38 个人所得税分配方案 数学建模(选修课)课程论文
安徽工程大学数学建模(选修课)课程论文题目:个人所得税分配方案摘要:十届全国人大常委会第十八次会议于2005年10月27日下午高票表决通过关于修改个人所得税法的决定,修改后的个人所得税法自2006年1月1日起施行。
此次个人所得税法,在两处进行了修改。
其中第六条第一款第一项修改为:“工资、薪金所得,以每个月收入额减除费用一千六百元后的余额,为应纳税所得额。
”同时,对“个人所得税税率表一”的附注作相应修改。
这即意味着个人所得税的起征点正式由现行的八百元,提高至一千六百元。
个人所得税法还特别加强了对高收入者的税收征管。
新法第八条修改为:“个人所得税,以所得人为纳税人,以支付所得的单位或者个人为扣缴义务人。
个人所得超过国务院规定数额的,在两处以上取得工资、薪金所得或者没有扣缴义务人的,以及具有国务院规定的其他情形的,纳税义务人应当按照国家规定办理纳税申报。
扣缴义务人应当按照国家规定办理全员全额扣缴申报。
”关键词:个人所得税;纳税优化;贷款方案;规划求解队员1:薛山(电气工程及其自动化、电气111、3110205141)队员2:沙童飞(电气工程及其自动化、电气111、3110205122)指导老师:周金明成绩:完成日期:2012.11.7一、问题重述广受社会关注的个人所得税起征点标准,2005年10月27日下午尘埃落定。
全国人大常委会高票表决通过关于修改个人所得税法的决定,修改后的个人所得税法自2006年1月1日起施行。
此次个人所得税法,在两处进行了修改,调整工薪所得费用扣除标准和扩大纳税人自行申报范围两项政策调整:一是提高了工薪所得费用扣除标准,个税起征点:1600元 ,个税法第六条第一款第一项修改为:“工资、薪金所得,以每个月收入额减除费用1600元后的余额,为应纳税所得额。
”二是进一步扩大纳税人自行申报范围和推行扣缴义务人全员全额扣缴申报,加大对高收入者的征管力度,堵塞税收漏洞。
其具体征税方案如下:一、每月工资应纳税计算方案:月应纳税所得额=月工薪收入-费用扣除标准(1600)超额累进税率级数月应纳税所得额税率(%)1 不超过500元部分 52 超过500元至2000元的部分103 超过2000元至5000元的部分154 超过5000元至20000元的部分205 超过20000元至40000元的部分256 超过40000元至60000元的部307 超过60000元至80000元的部分358 超过80000元至100000元的部分409 超过100000元的部分45例如:如某人月工薪收入为3500元,则月应纳税所得额=3500-1600=1900元,当月应交个人所得税=500×5%+(1900-500)×10%=165元。
个人所得税起征点
个人所得税起征点个人所得税是对个人(自然人)取得的各项所得征收的一种所得税,个人所得税起征点是指国家为了完善税收体制,更好的进行税制改革,而制定的税收制度。
2011年4月20日十一届全国人大常委会第二十次会议召开,个人所得税免征额拟调至3000元。
计算方式征缴个人所得税的计算方法,个税起征点原来是2000,使用超额累进税率的计算方法如下:缴税=全月应纳税所得额*税率-速算扣除数全月应纳税所得额=(应发工资-四金)-2000实发工资=应发工资-四金-缴税扣除标准:2008年3月份起,个税按2000元/月的起征标准算个人所得税征收范围:包括工资薪金所得;个体工商户生产、经营所得;对企事业单位的承包经营、承租经营所得;劳务报酬所得;稿酬所得;特许权使用费所得;利息、股息、红利所得;财产租赁所得;财产转让所得;偶然所得;经国务院财政部门确定征税其他所得。
公众对“起征点”存在误解。
正确的说法应该是“个人所得税免征额”。
“起征点”与“免征额”有着严格的区别。
在财政学中,起征点与免征额是不同的两个概念,不能混用,否则无法区分税法中的一些规定。
所谓起征点,是征税对象达到征税数额开始征税的界限。
征税对象的数额未达到起征点时不征税。
一旦征税对象的数额达到或超过起征点时,则要就其全部的数额征税,而不是仅对其超过起征点的部分征税。
所谓免征额是在征税对象总额中免予征税的数额。
它是按照一定标准从征税对象总额中预先减除的数额。
免征额部分不征税,只对超过免征额部分征税。
二者的区别是:假设数字为2000,你当月工资是2001,如果是免征额,2000就免了,只就超出的1块钱缴税,如果是起征点,则是不够2000的不用交税,超出2000的全额缴税,即以2001元为基数缴税。
历程1981年,个人所得税正式开征,当年个税收入只有500万元。
月均收入能够达到800元起征标准的中国公民少而又少,其余都是外籍在华高级职员交纳的。
1986年9月,国务院发布了《中华人民共和国个人收入调节税暂行条例》,规定对本国公民的个人收入统一征收个人收入调节税,纳税的扣除额标准(即起征点)降低至400元。
新个人所得税5000起征点正算以及倒推反算公式模板
新个人所得税5000起征点正算以及倒推反算公式模板-不超过3000元的部分,税率为3%;
下面我们来介绍如何计算个人所得税以及倒推反算公式模板。
计算个人所得税:
1.首先,需要先计算出应纳税所得额。
个人所得税的起征点为5000元,所以我们需要减去5000元。
2.接下来,根据应纳税所得额,按照相应的税率进行计算。
将应纳税所得额按照不同的税率段进行累计计算,并相加得出个人所得税的金额。
3.最后,将个人所得税金额扣除相应的减免税额,并得出最终需要缴纳的个人所得税。
倒推反算公式模板:
1.首先,我们需要知道税前收入。
2.然后,根据对应的税率档次,倒推出纳税金额。
3.最后,将纳税金额加上5000元得到税后收入。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于个人所得税起征点的数学模型
程敬松吉林交通职业技术学院
【摘要】本文对公众普遍关注的2011年《中华人民共和国个人所得税法修正案》中“个税起征点”这一热点问题进行了统计分析。
采用统计分析法对个人所得税与人均GD。
的关系进行定量和定性的分析,建立了个税起征点预测模型。
【关键词】个税起征点几何平均值滑动增长模型
中华人民共和国个人所得税法修订案[2011]中华人民共和国主席令(第69号)拟将工薪所得减除标准调高至3500元/月,财政部给出如下解释:据国家统计局资料,2010年度中国城镇居民人均消费性支出(包括基本生活支出和非基本生活必需品支出)为1123元/月,按平均每一就业者负担1.93人计算,城镇就业者人均负担的消费性支出为2167元/月。
2011年按城镇就业者人均负担的消费性支出增长10%测算,约为2384元/月。
综合考虑各方面因素,草案拟将减除费用标准由现行的2000元/月提高到3500元/月。
由于该修订案主要依据中国城镇居民人均消费性支出的变化来确定个税起征点,较少关注人均GD。
增长率、通货膨胀率等对个人所得税增长的影响。
因此,我们通过分析个人所得税增长率与人均GD。
增长率和通货膨胀率的变化趋势,以及人均GD。
和居民人均消费支出的变化趋势,建立合理的个税起征点预测模型。
一、个人所得税增长率、通货膨胀率和人均GD。
增长率的趋势分析为了能从总体上对人均GD。
增长率、通货膨胀率和个人所得税增长率三者之间的关系有一个直观的认识,下面利用我国近年来的相关经济数据(国家统计局网站),分析了人均GD。
增长率、通货膨胀率和个人所得税增长率随时间变化趋势(图1),人均GD。
增长率、通货膨胀率和个人所得税增长率在总体上的变化趋势基本上是一致的,具有同方向变化的趋势。
二、人均GD。
和居民人均消费支出的趋势分析为了保证时间序列的平稳性,利用人均GD。
(Y)和人均消费支出(X)的年度数据进行对数处理分析。
经分析发现Y和X存在协整关系。
首先,进行lnY和lnX进行相关性检验,得出两个变量之间的相关系数达到0.993,证明两者之间存在很强的相关性。
另外,由变量lnY和lnX的走势图(图2)分析,两者具有共同的增长趋势。
也就是说Y逐年增长,X也随之上升,因此个人所得税的起征点也应相应提高。
图1通胀率、人均GD。
增长率和个人所得税收入增长率随时间的变化趋势图图2变量和的走势图三、合理个税起征点的求解模型1.个人所得税起征点的
增长率。
通过上面人均GD。
和居民人均消费支出的趋势分析知道,GD。
是消费原因,从协整方程来看消费将随着GD。
的变化而变化,也就是说Y逐年增长,X也跟着上升,而且知道lnY变化是lnX变化的相伴概率是0.2365,而个人所得税的起征点随GD。
的变化而变化的同时,也是受到通胀率C。
I变化的影响。
设函数Xi为个人所得税第i年的增长率(2000年为第一年),αi表示GD。
第i年的增长率,βi表示C。
I第i年的增长率,建立模型如下:Xi=[1/(1+0.2365]×αi+[0.2365/(1+0.2365]×βi(1)为了方便计算我们取平均值,利用几何平均值的公式,得个税起征点平均增长率值XX=10Π101槡Xi(2)公式(1)(2)的运算结果如表1,得个人所得税增长率X为12.45%。
表1个人所得税增长率X计算年份GD。
增长率%C。
I增长率%X%X%20009.768.069.4320019.726.449.0920029.0011.169.41200312.1710.3311.82200417.0110.3115.73200515.0010.5914.1520061
6.329.4915.01200722.2414.9620.85200817.5412.46_________16.5720097.889.098.1112.452.建立起征点滑动增长模型。
设函数yi为第i年的个人所得税起征点(2000年为第一年),变量ρ为个税起征点的增长率,D为初始起征点,即1600元,理论上起征点应在第t年实施的,但实际上由于年度数据统计的滞后性问题,起征点将会在t+1年实施。
于是得到模型如下:yi=D(1+ρ)j-2(3)取个税起征点的增长率ρ为12.45%,其合理性3.1中已证明。
为了方便相关部门展开工作,现在对所得税的数据进行磨光处理:Yi=[y1100]×100(4)经计算得,2010年的起征点y8为4090元,2011年的起征点y9为4600元,磨光处理得:2010年的起征点y8为4100元,2011年的起征点y9为4600元,为现行的起征点3500元的1.3倍,这有利于减轻绝大多数中低收入的经济负担,也使中高收入阶层成为个税征收的主要对象。
充分体现了个人所得税缩短贫富差距的作用。
该模型通过与GD。
联动,也就是个税随GD。
的增幅同比例的向上浮动,或随C。
I的浮动而浮动。
当经济发展良好,GD。
就上升,个税起征点也上升;当经济衰退时,GD。
就下降,这与现行方案的个税起征点定制有一个质的飞跃,使得税收调节功能滞后相对较短,灵活,易于控制。
参考文献:
吴云飞,我国个人收入分配税放调控研究[M],上海;复旦大学出版社,2001;1-80
刘承平,数学建模方法[M],北京;高等教育出版社,2002;13-1300.
刘振航,数学建模[M],北京;中国人民大学出版社,2004;50-100.54财税金融 __。
