雷达成像基本算法
机载聚束模式合成孔径雷达的成像算法

基于图像聚焦与运动补偿的改进算法
总结词
详细描述
该算法通过引入图像聚焦和运动补偿技术, 实现了对运动目标和复杂背景的高分辨率成 像。
基于图像聚焦与运动补偿的改进算法,通过 对运动目标和复杂背景进行聚焦和补偿处理 ,提高了成像的分辨率和对比度。该算法具 有较高的计算复杂度,但能够提供高质量的 SAR图像,适用于对运动目标和复杂背景的
实验结果展示与分析
结果展示
将机载聚束模式合成孔径雷达的原始回波数据转化为 地物图像,并进行对比分析。
结果分析
通过与实地采集的地物图像进行对比,验证了机载聚 束模式合成孔径雷达的成像效果。
成像算法性能评估与对比分析
性能评估:评估机载聚束模式合成孔径雷达的成像算法在分辨率、对比度、清晰度等方面的性能指 标。
机载聚束模式合成孔径雷达 的成像算法
2023-11-06
目 录
• 成像算法概述 • 聚束模式SAR基本成像算法 • 改进型聚束模式SAR成像算法 • 成像算法的优化与实现 • 成像算法验证与分析 • 结论与展望
01
成像算法概述
合成孔径雷达(SAR)基本原理
合成孔径雷达是一种雷达成像技术,通过在飞行器上安装雷达天线,利用目标的 反射信号,生成高分辨率的图像。
数据输出与显示
将成像结果和目标信息进行输出和 显示,为后续任务提供决策支持。
05
成像算法验证与分析
实验场景与数据采集
实验场景
机载聚束模式合成孔径雷达(CS-SAR)在城市、农田、 山丘等典型地物场景中进行实验。
数据采集
采集不同飞行高度、速度、姿态等条件下的雷达回波数 据,以及对应的地物图像数据。
除了军事应用外,该成像算法也可应用于民用航空领域,例如机场跑道检测、地形测绘、 气象观测等方面,具有广泛的应用前景。
雷达成像rd算法积分旁瓣比

雷达成像rd算法积分旁瓣比
雷达成像是一种利用雷达技术进行目标成像的方法,而积分旁
瓣比是评价雷达成像质量的重要指标之一。
积分旁瓣比是指成像过
程中目标信号与旁瓣(或者说杂波)信号之间的比值。
在雷达成像中,旁瓣通常是指由于雷达天线方向图、波束形状等因素引起的非
期望信号。
从技术角度来看,雷达成像中的积分旁瓣比是由雷达系统的性
能参数、成像算法以及目标场景等多个因素共同决定的。
首先,雷
达系统的天线方向图和波束形状会直接影响到旁瓣的产生,因此天
线设计和波束控制是影响积分旁瓣比的重要因素。
其次,成像算法
的设计也会对积分旁瓣比产生影响,比如在成像算法中采用的滤波、聚焦等处理方式会影响到目标信号和旁瓣信号的分离程度。
此外,
目标场景的复杂程度也会对积分旁瓣比产生影响,比如目标的反射
特性、背景干扰等因素都会影响到成像质量。
另外,从应用角度来看,积分旁瓣比的大小直接关系到雷达成
像的清晰度和目标分辨率。
较高的积分旁瓣比意味着目标信号相对
于旁瓣信号更突出,成像质量更高,目标的细节信息能够更加清晰
地呈现出来。
因此,在实际的雷达成像应用中,工程师们通常会根
据具体的成像要求和场景特点来调整雷达系统参数和优化成像算法,以获得更好的积分旁瓣比,从而获得更高质量的雷达成像结果。
总之,雷达成像中的积分旁瓣比是一个综合了技术、算法和应
用等多方面因素的重要指标,对于评价雷达成像质量和优化成像效
果具有重要意义。
雷达成像技术(保铮word版)第五章 合成孔径雷达成像算法

第五章 合成孔径雷达成像算法SAR 成像处理最初用光学处理,后来采用数字处理。
与光学处理相比,数字处理更精确、更灵活,在距离徙动校正、运动补偿、几何校正和坐标转换等方面有明显的优势。
SAR 成像处理主要有两个问题,一是距离徙动校正,二是运动补偿。
距离徙动可分解一次的线性分量和二次以上(包括二次)的弯曲分量,线性分量称为距离走动,弯曲分量称为距离弯曲。
这一章主要讨论针对不同距离徙动程度情况下,需要采用的不同成像算法,运动补偿将在下一章讨论。
5.1 距离徙动距离徙动对合成孔径雷达成像是一个重要的问题,虽然在前面已多次提及,这里还要对它作比较系统的介绍。
θ∆波束Qθ∆BR B ALxBR ROmvt x图5.1正侧视时距离徙动的示意图距离徙动的情况对不同的波束指向会有所不同,首先讨论正侧视的情况,这时距离徙动可用图5.1来说明。
所谓距离徙动是雷达直线飞行对某一点目标(如图中的Q 点)观测时的距离变化。
如图5.1所示,天线的波束宽度为θ∆,当载机飞到A 点时波束前沿触及Q 点,而当载机飞到B 点时,波束后沿离开Q 点,A 到B 的长度即有效合成孔径L ,Q 点对A 、B 的转角即相干积累角,它等于波束宽度θ∆。
Q 点到航线的垂直距离为最近距离B R 。
这种情况下的距离徙动通常以合成孔径边缘的斜距R 与最近距离B R 之差表示,即BB B q R R R R R -∆=-=2secθ (5.1)在合成孔径雷达里,波束宽度θ∆一般较小,2)(2112secθθ∆+≈∆,而相干积累角θ∆与横向距离分辨率a ρ有以下关系:θλρ∆=2a 。
利用这些关系,(5.1)式可近似写成:22232)(81aBB q R R R ρλθ=∆≈(5.2)假设条带场景的幅宽为W ,即场景近、远边缘与航线的最近距离分别为2W R B -和2W R B +,得场景两端的距离徙动差为2232a q WR ρλ=∆ (5.3)距离徙动和距离徙动差的影响表现在它们与距离分辨率r ρ的相对值,如果它们比r ρ小得多,就无需作包络移动补偿。
sar 常用成像算法

sar 常用成像算法SAR(Synthetic Aperture Radar)是合成孔径雷达的缩写,是一种利用雷达技术进行成像的方法。
常用成像算法是指在SAR成像过程中常用的数据处理方法,用于从原始雷达数据中提取目标信息并生成可视化图像。
本文将介绍几种常用的SAR成像算法。
一、Range-Doppler算法Range-Doppler算法是最基础、最常用的SAR成像算法之一。
它通过两个主要步骤来实现成像:距离向(Range)压缩和多普勒向(Doppler)压缩。
首先,进行距离向压缩,将接收到的信号与发射的信号进行相关运算,得到目标在距离上的分布信息。
然后,进行多普勒向压缩,根据目标的运动情况对信号进行频率调整,得到目标在速度上的分布信息。
最后,将两个方向上的信息进行合成,得到最终的成像结果。
二、Chirp Scaling算法Chirp Scaling算法是一种用于高分辨率SAR成像的算法。
它通过对原始SAR数据进行频率调整,实现对目标的高精度成像。
具体而言,该算法通过对接收到的信号进行线性调频,使得距离上的分布信息与目标的距离成线性关系。
然后,对调频后的信号进行快速傅里叶变换,得到目标在频谱上的分布信息。
最后,对频谱信息进行逆变换,得到目标在距离上的高分辨率成像结果。
三、Omega-K算法Omega-K算法是一种用于高分辨率SAR成像的频域算法。
它通过对SAR数据进行快速傅里叶变换,将时域数据转换为频域数据,然后根据目标的运动情况对频域数据进行调整,实现高分辨率成像。
具体而言,该算法通过对频域数据进行插值,使得目标的速度信息与频率成线性关系。
然后,对插值后的数据进行逆傅里叶变换,得到目标在距离上的高分辨率成像结果。
四、Polar Format算法Polar Format算法是一种用于SAR成像的快速算法。
它通过将SAR数据从直角坐标系转换为极坐标系,实现对目标的快速成像。
具体而言,该算法首先将原始SAR数据进行极坐标变换,得到距离和方位两个维度上的数据。
毫米波雷达成像算法

毫米波雷达成像算法
毫米波雷达成像算法主要包括以下步骤:
1.信号采集:通过雷达系统发射毫米波信号并接收目标反射的回波信号,获取包含目标信息的回波数据。
2.信号处理:对回波数据进行预处理,包括滤波、去噪、补偿等操作,以提高信号质量。
3.距离像估计:对处理后的回波数据进行距离像估计,得到每个目标点的距离像数据。
4.成像处理:对距离像数据进行成像处理,包括运动补偿、多普勒补偿、聚焦等操作,以提高成像质量。
5.目标检测与跟踪:在成像结果中检测并跟踪目标,提取目标的位置、速度、姿态等信息。
6.特征提取与分类:对目标进行特征提取和分类,以实现目标识别和分类。
在毫米波雷达成像算法中,信号处理和成像处理是关键步骤。
常用的信号处理算法包括匹配滤波器、自适应滤波器等;常用的成像处理算法包括频域成像、时域成像等。
为了提高算法性能,需要不断优化算法和参数选择,以适应不同的场景和应用需求。
雷达点目标成像
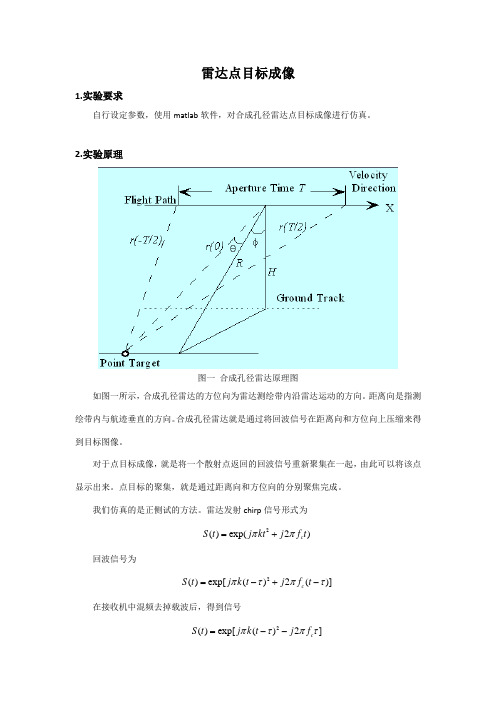
雷达点目标成像1.实验要求自行设定参数,使用matlab 软件,对合成孔径雷达点目标成像进行仿真。
2.实验原理图一 合成孔径雷达原理图如图一所示,合成孔径雷达的方位向为雷达测绘带内沿雷达运动的方向。
距离向是指测绘带内与航迹垂直的方向。
合成孔径雷达就是通过将回波信号在距离向和方位向上压缩来得到目标图像。
对于点目标成像,就是将一个散射点返回的回波信号重新聚集在一起,由此可以将该点显示出来。
点目标的聚集,就是通过距离向和方位向的分别聚焦完成。
我们仿真的是正侧试的方法。
雷达发射chirp 信号形式为2()exp(2)c S t j kt j f t ππ=+回波信号为2()exp[()2()]c S t j k t j f t πτπτ=-+-在接收机中混频去掉载波后,得到信号2()exp[()2]c S t j k t j f πτπτ=--可得信号的距离向信号形式为2exp[(2/)]j k t r c π-方位向信号形式为exp[4/]c j f r c π-其中()r t =当v t R 时有2()()2vt r t R R ≈+,知回波信号在方位向上也是线性调频信号,其调频率为22v Rλ,λ为载波波长。
对于成像算法,我们采用经典的距离多普勒算法,即SD 算法。
他的基本思想是基本思想是将二位处理分解为两个一维处理的级联方式,即分别压缩距离向和方位向。
由于雷达的飞行线路接近直线,所以方位向和距离向相互有影响,要对数据进行徙动校正。
但是由于机载SAR 飞行范围小,距离弯曲量很小,故可以不用考虑徙动校正。
SD 算法的具体流程图如图二所示。
图二 SD 算法的具体流程图4.实验过程参数设置:飞机飞行高度:10000m下视角:45度飞机的飞行速度:100m/s合成孔径时间:1sPRF :500HzK :113010⨯Hz/s脉冲宽度:10us载波频率: 10510Hz ⨯回波点阵大小:501X501对数据进行距离向压缩,得到图一。
雷达成像积分旁瓣比公式

雷达成像积分旁瓣比公式
雷达成像积分旁瓣比是衡量雷达成像系统图像质量的重要指标之一,它描述了成像系统在成像过程中对于干扰源的抑制能力。
积分旁
瓣比越大,表示成像系统对于干扰源的抑制能力越强,图像质量越好。
雷达成像积分旁瓣比的计算公式为:
SIR = 10 * log10(I_main / I_side)
其中,SIR表示积分旁瓣比,I_main表示主瓣内的能量,I_side
表示旁瓣内的能量。
积分旁瓣比的单位通常是分贝(dB)。
拓展:
雷达成像积分旁瓣比的大小受到多种因素的影响。
其中,主要因
素包括雷达天线的辐射特性、系统噪声、散射目标的分布以及采用的
成像算法等。
为了提高雷达成像积分旁瓣比,可以采取以下措施:
1.优化雷达天线辐射特性:通过调整天线方向图、天线孔径大小、天线波束宽度等参数,减小旁瓣的能量。
2.降低系统噪声:采用低噪声放大器、有效的信噪比增益技术等,以提高系统的信噪比,从而减小旁瓣的能量。
3.优化成像算法:选择适合的成像算法,如谱分析法、波束形成
方法等,以提高图像的分辨率和对干扰源的抑制能力。
4.控制散射目标分布:通过对目标的选取、分类、滤波等处理,
减小干扰目标对成像结果的影响,进而提高积分旁瓣比。
综上所述,雷达成像积分旁瓣比是一个衡量雷达成像系统图像质
量的指标,通过优化天线辐射特性、降低系统噪声、优化成像算法以
及控制散射目标分布等手段,可以提高积分旁瓣比,从而改善雷达成
像系统的成像效果。
SAR成像及成像算法

SAR成像及成像算法
SAR(Synthetic Aperture Radar),即合成孔径雷达,是一种具有视距的雷达成像技术,它利用通过雷达发射的电磁波的返回信号来构建成像,是今天最受欢迎的遥感成像技术之一、它是由空间技术应用罗列公司(STARS)于1970年首次研制完成的。
由于它的无损探测、低成本、通用性强、快速更新和相当高的精度等优点,使SAR成像广泛应用于地表特性探测、航空和海洋地理资源监测、地表热分辨观测、大气和气候研究等多种领域,并取得了突出的成果。
SAR成像的本质是利用雷达发射的电磁波探测地表物质的反射状态,从而构建三维图像。
SAR成像算法主要分成基线分析、多普勒解析和像元投影三个过程。
首先,基线分析是处理多普勒解析的基本步骤,它识别SAR图像的物理位置,将地表物质的反射信号与它们在同一物理位置的多普勒频率作对比,从而计算出相应的基线;其次,多普勒解析处理SAR图像所涉及的空间结构,它可以利用反射信号的多普勒频率,将不同波段中的多普勒信号重建成三维定量数据;最后,像元投影过程会将三维数据转换成二维图像,以实现SAR成像。
当前。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2Vr2 f 0 f 。 cR0
1.2.2 一般情况下的信号频谱
为了获得双曲距离等式的信号频谱,可进行如下操作:(1) 距离向 FFT;(2) 方位 向 FFT;(3) 距离向逆 FFT。其中前两步得到二维频域表达式,最后一步得到距离多普 勒域表达式。 将信号进行距离向 FFT,利用驻定相位原理,得到 距离频域的表达式
D2 df f , f , Vr 1
c 2 f2 4Vr2 f 0 f c 2 f2 4Vr2 f 0 f
2 2
,则
Vr2 2 R 2
1
(1.2.13)
由于 D2df(fτ, fη, Vr)就是直线几何中方位时刻 η 时的斜视角 θr 的余弦值,且距离徙动可以 表示为 R0 / cosθr 的形式,因此,D2df(fτ, fη, Vr)称为二维频域中的徙动因子。为了给出不 同相位项的显示表达式,令 D f , Vr 1
c 2 f2 4Vr2 f 02
,则二维频域的表达式为
s2 df f , f A0 A1 A2Wr f Wa f fc f2 4 R0 f 0 exp j exp j Kr c
2 f f2 2 f0 f0 (1.2.14)
c 2 f2
可以忽略。第一项代表方位向调制,第二项代表距离徙动,第三项代表距离和方位的交 叉耦合。下面,可以直接写出傅立叶积分中的相位
c 2 f2 f2 f f2 4 R0 f 0 2 3 2 f (1.2.16) D f , Vr c 4Vr2 f 02 K r f D f V f D f V , 2 , 0 0 r r
其中,常数 A1 含有一个 / 4 的相位,但它对下面的分析并不重要。 将信号进行方位向 FFT,利用驻定相位原理处理时,公式比较繁琐,下面给出推导 过程。傅立叶积分中的相位为
4 f 0 f R f2 2 f c Kr
(1.2.9)
(1.2.2)
将信号进行方位向 FFT,利用驻定相位原理,得到 普勒域的频谱
,从而可以得到距离多
2 Rrd f Wa f fc srd , f A0r c 2 2 Rrd f f2 4 exp j R exp j exp j K r c 0 Ka
下面给出典型的机载和星载条带 SAR 的参数。 表 1-1 机载和星载 SAR 的典型参数 参数 距离向参数 景中心距离 高度 发射脉冲时宽 距离脉冲调频率 信号带宽 距离采样率 斜距条带宽度 方位向参数 雷达有效速度 雷达工作频率 雷达工作波长 方位调频率 合成孔径长度
6
符号
机载
星载
单位
R(ηc) Tr Kr Fr
信号的二维频域表达式可以表示为
(1.2.10)
cR0 f 2 f 0 f Vr2 1 c 2 f2 4Vr2 f 0 f
2
。于是,
f2 s2 df f , f A0 A1 A2Wr f Wa f fc exp j Kr c 2 f2 4 R0 f 0 f exp j 1 2 2 c 4Vr f 0 f
(1.2.4)
其中,Rrd 为该域中的距离徙动量,其表达式为 Rrd f R0 这是一条关于 fη 的抛物线。 对 距 离 多 普 勒 域 的 信 号 进 行 距 离 向 FFT , 利 用 驻 定 相 位 原 理 , 得 到
2 R0
8V
2 r
f2
(1.2.5)
f 2 Rrd f ,从而可以得到二维频域的频谱 Kr c
4 f 0 f R f2 s0 f , A0 AW exp j (1.2.8) 1 r f a c exp j Kr c
f 2 R ,从而可以得到 Kr c
(1.2.11)
其中,包络 Wa 的表达式为
4
cR0 f Wa f a c 2 f2 2 2 2 f 0 f Vr 1 2 4Vr f 0 f
(1.2.12)
用符号 D2df(fτ, fη, Vr)表示根号项 1
1 Kr
2Vr2 f 03 D 3 f , Vr
Kr cR0 f2
2 R0 ,代入积分表达式,得到 cD f V , r
距离多普勒域的表达式为
2 R0 srd , f A0 A1 A2 A3r K m Wa f fc cD f ,Vr 2 2 R0 4 R0 D f ,Vr f 0 exp j exp j K m c cD f , V r
c 2 f2 f f2 2 f f2 2 D f , Vr D f , Vr f0 f0 f 0 D f , Vr 2 f 02 D 3 f , Vr 4Vr2 f 02
2
2
(1.2.15)
2 f f2 该近似是对根式的 Taylor 展开,当 D f , Vr 1 2 2 2 时,展开的高次项 4Vr f 0 f0 f0
(1.2.6)
假设 f0 >> |fτ|,Ka 中的距离向频率 f0 由 f0 + fτ 所代替,则二维频域的频谱可以简化为
3
s2 df f , f A0Wr f Wa f fc
(1.2.7)
f2 4 f 0 f f2 R0 exp j exp j exp j Kr c Ka '
f
因此,θ(fτ)对 fτ 的导数为
cR0 f2 d f 4 R0 2 f f 2 2 2 3 3 df Kr cD f ,Vr 2Vr f 0 D f ,Vr
(1.2.17)
5
令
d f 0 ,则 f df
第1章 条带模式合成孔径雷达
1.1 基本定义和几何模型
图 1-1 单站条带 SAR 几何模型
1.2 回波信号频谱
基于处理效率考虑,大多数 SAR 处理算法都工作在频域,其中匹配滤波和距离徙 动校正(RCMC)是首要考虑的效率因素。在方位频域,最短斜距相同的目标具有一致的 距离徙动轨迹,这样使得在该域中应用 RCMC 较为方便。因此,对距离多普勒域和二 维频域中的 SAR 信号频谱的推导是十分有用的。 1.2.1 信号频谱的抛物线近似 对于诸如 ERS 或 RADARSAT 这样具有小斜视角和中等孔径长度的传感器, 双曲距
D 2 f ,Vr
其中,常数 A2 含有一个无关紧要的 / 4 的相位。在数字处理器实现中,先进行距离向
FFT 还是方位向 FFT 并不重要。在任何情况下,二维信号频谱都可以用以上等式精确表
达。 对二维频域的信号进行距离向逆 FFT,直接应用驻定相位原理,会导致出现 fτ 的四 次方程,使得代数求解过程冗长。为避免繁琐的代数处理,作如下近似
目标照射时间 天线长度 多普勒带宽 方位采样率(PRF) 斜视角
Ta La Δfdop Fa θr,c
3.4 1 443 600 <8
0.64 10 1338 1700 <4
s m Hz Hz °
根据典型的机载和星载参数,我们画出回波信号在不同域中的图形,如下:
(a)
(b)
7
(c)
(d)
图 1-2 典型机载参数的 SAR 回波:(a) 正调频时域回波信号(相位);(b) 负调频时域回 波信号(相位);(c) 回波信号的二维频域(幅度);(d) 回波信号的距离-多普勒域(幅度)
将瞬时斜距表达式代入,得到 θ(η)对 η 的导数为
d 4 f 0 f Vr2 2 f d c R02 Vr2 2 2Vr2 f 0 f d 令 0 ,则 f 或 d c R02 Vr2 2
第一步,将回波信号通过二维 FFT,将数据变换到二维频域,结果如下
s2 df f , f AWr f Wa f fc
(1.3.1)
f2 4 f R0 4 R0 exp j exp j D f ,Vr exp j Km cD f , Vr
(1.2.18)
其中, K m
1 Kr
2Vr2 f 03 D 3 f , Vr
Kr cR0 f2
为新的距离调频率,常数 A3 含有一个无关紧要的
/ 4 的相位。距离向包络 ωr 表示距离徙动,第一个指数项为有距离徙动引起的方位向
调制,第二个指数项为距离向调制。
1.2.3 条带 SAR 的典型参数
(a)
8
(b)
(c)
(d)
图 1-3 典型机载参数的 SAR 回波:(a) 正调频时域回波信号(相位);(b) 负调频时域回 波信号(相位);(c) 回波信号的二维频域(幅度);(d) 回波信号的距离-多普勒域(幅度)
9
1.3 Range-Doppler 成像算法
1.3.1 Range-Dopper 算法流程
2
离等式可以进行抛物线近似 R R02 Vr2 2 R0 于是,基带接收信号可以近似为 2 R s0 , A0r a c c 2 2 R 4 2 exp j R0 exp j K a exp j K r c 其中方位向调频率 Ka 为 Ka 2Vr2 2Vr2 f 0 R0 cR0 f Ka (1.2.3) Vr2 2 2 R0 (1.2.1)
