物理化学_计算题
物理化学试题集计算题

1.在298.15K 及p θ下,过冷水蒸气变为同温同压下的水,求此过程的⊿G 。
已知298.15K 时水的饱和蒸气压为3167Pa 。
解:⊿G=⊿G 1+⊿G 2+⊿G 3=J85901013253167ln 15.298314.81ln 021122112-=⨯⨯⨯==≈++⎰⎰⎰p p g p p l p p g p p nRT dp V dpV dp V或J 23.8588)3167101325(110018.010********ln15.298314.81)(ln032112211221-=-⨯++⨯⨯⨯=-+=∆+=++-⎰⎰⎰p p l l g p p l p p g p p V p p nRT P V dp V dp V dp V2.在298.15K 及p θ下,过冷水蒸气变为同温同压下的水,求此过程的⊿G 。
已知298.15K 时水的饱和蒸气压为3167Pa 。
3.已知反应C(石墨)+CO 2(g)=2CO(g)r m G θ∆(1000K)=-3.4 k J ·mol -1,计算(1) 1000K 时该反应的平衡常数。
(2)当p (CO)=200kPa, p (CO 2)=800kPa 时,判断该反应方向。
解:(1)410775.11000314.8303.24.3)1000(lg -⨯=⨯⨯--=K K θK θ=1.00(2)方法一2.303lg r m G RT K θθ∆=-∵⊿r G m(1000K)<0,∴反应正向自发进行方法二Q=(200/100)2/(800/100)=4/8=0.5Kθ=1.00∵Q<Kθ∴反应正向自发进行4.某抗菌素在人体内的代谢反应为一级反应,若服药后每24小时药物代谢一半,而药物代谢20%则必须补充该药,问第二次服药时间?解:t1/2=0.693/kk=0.693/24=0.028875(小时)-1ln(C0/C A)=ktt=7.73(小时)5.Zn-Hg(含Zn10%)∣ZnSO4·7H2O(s)饱和溶液‖Hg2SO4(s)(饱和溶液)∣Hg(l)。
物理化学习题-含答案
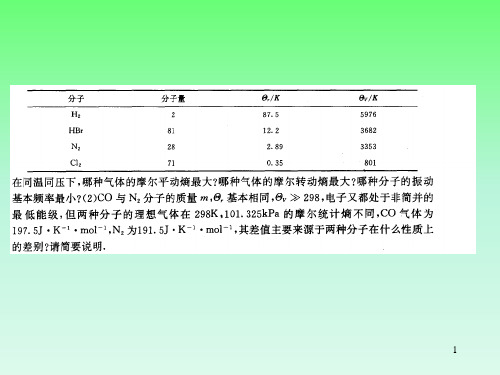
基态是单态。计算在298K、1atm下一氧化碳气体的 摩尔熵值。
7
解:由于CO气体为非定位体系,其熵公式为:
ln Q Q NkT S k ln N! T
N
ln Q Nk ln Q k ln N! NkT T
可将其看成是体系的平动熵、转动熵、振动熵及电子熵等之 和。可先分别求出各运动形式的熵、再求和而得体系的总熵 。上式的-k lnN! 项归入平动熵计算。
32
将题中给出的数据直接代入上式得:
Q转
2 8 1.1461045 1.381023 298 (3.1416 )
2 (6.62610
34 2
)
424
5
(3)如果将分子看成是谐振子,则有
Q振 1 1 e h kT 1 1 e h c kT
由题意知,
565cm1 565102 m1
~
1 代入上式得: Q振 6.6261034 565102 2.998108 1 exp[ ] 23 1.3810 298
1
1 e
2.73
1.07
6
计算题
2.已知一氧化碳分子的转动惯量是
I 1.451046 kg m2 ~ 1 基本振动波数 2170cm ,分子量为 28.0,其电子
2170cm1 217000 m1
ln Q h c e h c kT T kT2 1 e h c kT
12
将数据代入得
ln Q振 T
计算题
10.5 e10.5 0 10.5 298 (1 e )
S振 R ln Q振 RT T 8.314 ln 1 8.314 298 0 0
物理化学试卷及答案3套

物理化学试卷及答案3套三、计算题( 共5题60分)21. 10 分(0824)计算1mol He(理想⽓体) 在下列状态变化过程中的ΔH和ΔG。
He (101.325 kPa,473 K)??→He (101.325 kPa,673 K)已知:C p, m [He(g)] = (5/2)R,473K 时S m$[He(g)] = 135.1 J·K-1·mol-1。
22. 15 分(1104)某⽓体状态⽅程为pV = n(RT + Bp),始态为p1T1,该⽓体经绝热真空膨胀后终态压⼒为p2,试求该过程的Q,W及⽓体的ΔU,ΔH,ΔF,ΔG,ΔS。
23. 10 分(1809)两液体A, B形成理想液体混合物。
在320 K,溶液I含3 mol A和1 mol B,总蒸⽓压为:5.33×104 Pa。
再加⼊2 mol B 形成理想液体混合物II,总蒸⽓压为6.13×104 Pa。
(1) 计算纯液体的蒸⽓压p A*,p B*;(2) 理想液体混合物I的平衡⽓相组成y B;(3) 理想液体混合物I的混合过程⾃由能变化Δmix G m;(4) 若在理想液体混合物II中加⼊3 mol B形成理想液体混合物Ⅲ,总蒸⽓压为多少?24. 15 分(2419)固体CO2的蒸⽓压与温度间的经验式为:ln(p/Pa)=-3116 K/T + 27.537已知熔化焓?fus H m= 8326 J·mol-1,三相点的温度为217 K。
试求出液体CO2的蒸⽓压与温度的经验关系式。
25. 10 分(2965)3H2+ N2= 2NH3在350℃的K p= 6.818×10-8(kPa)-2,并设与压⼒⽆关,从3:1的H2,N2混合物出发,在350℃下要获得物质的量分数为0.08 的NH3,压⼒⾄少要多⼤?26. 13 分(0957)4 g Ar(可视为理想⽓体,其摩尔质量M(Ar)=39.95 g·mol-1)在300 K时,压⼒为506.6 kPa,今在等温下反抗202.6 kPa的恒定外压进⾏膨胀。
物理化学习题

物理化学习题题目一某物质的熔点为100°C,沸点为200°C。
若将36g的该物质从液态加热到气态,需要吸收多少热量?已知该物质的熔化热为40 cal/g,汽化热为80 cal/g。
解答:首先计算熔化过程需要的热量。
根据熔化热的定义,熔化过程需要的热量可以通过以下公式计算:Q = m * ΔHf其中,Q为热量,m为物质的质量,ΔHf为熔化热。
将已知数据代入公式计算:Q1 = 36g * 40 cal/g = 1440 cal接下来计算汽化过程需要的热量。
根据汽化热的定义,汽化过程需要的热量可以通过以下公式计算:Q = m * ΔHv其中,Q为热量,m为物质的质量,ΔHv为汽化热。
将已知数据代入公式计算:Q2 = 36g * 80 cal/g = 2880 cal所以,将36g的该物质从液态加热到气态需要吸收的总热量为:Q总 = Q1 + Q2 = 1440 cal + 2880 cal = 4320 cal题目二某有机物A的摩尔热容为25 J/(mol·K),某有机物B的摩尔热容为40J/(mol·K)。
已知在一定温度下,物质A和物质B的摩尔比为1:2,试求混合物的摩尔热容。
解答:首先计算物质A和物质B在混合物中所占的摩尔数。
根据题目中给出的摩尔比,我们可以设物质A的摩尔数为x,物质B的摩尔数为2x。
根据摩尔热容的定义,摩尔热容可以通过以下公式计算:C = Q / (n * ΔT)其中,C为摩尔热容,Q为热量,n为物质的摩尔数,ΔT为温度变化。
将物质A和物质B的摩尔热容代入公式计算:C_A = 25 J/(mol·K) C_B = 40 J/(mol·K)混合物的总摩尔数为x + 2x = 3x。
根据题目中给出的温度变化,假设为ΔT,混合物的热量可以通过以下公式计算:Q = C_A * n_A * ΔT + C_B * n_B * ΔT将已知的摩尔热容和摩尔数代入公式计算:Q = 25 J/(mol·K) * x * ΔT + 40 J/(mol·K) * 2x * ΔT = 25x ΔT + 80x ΔT = 105x ΔT所以混合物的摩尔热容为:C_混合物 = Q / (n_混合物* ΔT) = (105x ΔT) / (3x * ΔT) = 35 J/(mol·K)题目三某物质的密度为2.5 g/mL,摩尔质量为40 g/mol。
物理化学计算题(2003版本)

第一、二章:热力学1. 2mol 单原子理想气体在298.2K 时,分别按下列三种方式从15.00dm 3膨胀到40.00dm 3:1)等温可逆膨胀;2)等温对抗100kPa 外压;3)在气体压力与外压力相等并保持恒定下加热。
求三种过程的Q\W\ΔU 和ΔH 。
解:1) 因为理想气体的热力学能和焓都只是温度的函数,所以等温过程ΔU=ΔH=0W=-nRTln =-2*8.314*298.2ln =-4863 JQ=-W=4863 J2) 同理,ΔU=ΔH=0W=-p e (V 2-V 1)=-100*103*(40.00-15.00)*10-3=-2500 JQ=-W=2500 J3) 气体压力为:P= = =330.56kPaW=-330560*(40.00-15.00) *10-3=-8264JT 2= = =795.2KΔH=Qp=nC p,m (T2-T1)=n* R(T2-T1)= 2* *8.314*(795.2-298.2)=20660 JΔU=nC v,m (T2-T1)= 2* *8.314*(795.2-298.2)=12396 J或 ΔU=Q+W=20660-8264=12396 J2. 3mol 单原子理想气体从300K ,400kPa 膨胀到最终压力为200kPa.若分别经1)绝热可逆膨胀;2)绝人等外压200kPa 膨胀至终态。
试计算两种过程的W/E/ΔU/ΔH.解:1) 此过程的始、终态如下:绝热可逆膨胀对于单原子理想气体,则:r=C p,m /C v,m =(5/2R)/(3/2R)=5/3=1.67据理想气体的绝热可逆过程方程求T2T 1r p 11- r = T 2r p 21- r 代入T 1\p 1\p 2求得:3001.67*4001-1.67=T 21.67*2001-1.67T 2=227K因为绝热过程,Q=0,则:W= ΔU=nC v,m (T 2-T 1)=3*3/2*8.314*(227-300)=-2731JΔH=nC p,m (T 2-T 1)=3*5/2*8.314*(227-300)=-4.552J2) 此过程为绝热不可逆过程,始、终态如下:绝热等膨胀因为绝热过程,Q=0,则:W= ΔU=nC v,m (T 2-T 1)W=-p e (V2-V1)=-p2(V2-V1)V2= V1=所以W= ΔU=nC v,m (T 2-T 1)=-p 2( )3*3/2*8.314*(T 2-300)=-3*8.314*T 2+200/400*3*8.314*300T2=240KW= ΔU=nC v,m (T 2-T 1)=3*3/2*8.314*(240-300)=-2245JΔH=nC p,m (T 2-T 1)=3*5/2*8.314*(240-300)=-3741J3. 试求100kPa 、1mol 的286K 过冷液体苯变为固体苯的ΔS ,并判断此凝固过程是否可能发生。
物理化学期末考题(四,计算题参考答案)

仅供参考,请勿外传计算题参考答案1.1mol 单原子理想气体的始态为300K ,500kPa 。
(1)在等温条件下向真空膨胀至100kPa ,求此过程的Q 、W 、U ∆、H ∆、S ∆、A ∆、G ∆。
(2)在恒压条件下,体积增至原来的两倍(V 2=2V 1), 求此过程的Q 、W 、U ∆、H ∆、S ∆。
解:(1) 因为向真空膨胀,等温过程,故:01=Q ,01=W ,01=∆U ,01=∆HJ 4014kPa500kPa100ln K 300K mol J 8.314mol 1ln111211-=⨯⨯⋅⋅⨯==∆=∆--p p nRT G A 111211K J 38.13kPa100kPa 500ln K mol J 8.314mol 1ln---⋅=⨯⋅⋅⨯==∆p p nR S (2) 因为12212,V V p p ==,所以,由111222T V p T V p =,得K 600212==T T J 6236K 300)(600K m o l J 8.31425m o l 1)(1112m ,22=-⨯⋅⋅⨯⨯=-==∆--T T nC Q H p J 3741K 300)(600K m o l J 8.31423m o l 1)(1112m ,2=-⨯⋅⋅⨯⨯=-=∆--T T nC U V J 2495J 6236J 3741222-=-=-∆=Q U W1K600K300m,m ,2K J 4.14K300K600ln 8.314251d 1d 21-⋅=⨯⨯=⨯==∆⎰⎰T TC T TnC S p T T p2.1mol 理想气体,始态压力202650Pa ,体积为22.4dm 3,连续经历下列三个过程达到终态。
(1) 从始态可逆膨胀至B ,其压力为101325Pa ;(2)从B 再等容加热至C ,其温度为1091.9K ; (3)从C 再在等压条件下冷却至终态D ,其温度为545.9K 。
大学物理化学试题及答案

物理化学试卷一一、选择题 ( 共15题 30分 )1. 以下诸进程可应用公式 dU = (Cp- nR)dT进展计算的是: ( C )(A) 实际气体等压可逆冷却(B) 恒容搅拌某液体以升高温度(C) 理想气体绝热可逆膨胀(D) 量热弹中的燃烧进程2. 理想气体经可逆与不可逆两种绝热进程: ( B )(A) 能够从同一始态动身抵达同一终态因为绝热可逆ΔS = 0(B) 从同一始态动身,不可能抵达同一终态绝热不可逆S > 0(C) 不能判定 (A)、(B) 中哪一种正确因此状态函数 S 不同(D) 能够抵达同一终态,视绝热膨胀仍是绝热紧缩而定故终态不能一样3. 理想气体等温进程的ΔF。
( C )(A)>ΔG (B) <ΔG (C) =ΔG (D) 不能确信4. 以下函数中为强度性质的是: ( C )(A) S (B) (G/p)T(C) (U/V)T 容量性质除以容量性质为强度性质 (D) CV5. 273 K,10p下,液态水和固态水〔即冰〕的化学势别离为μ(l) 和μ(s),二者的关系为:( C )(A) μ(l) >μ(s) (B) μ(l) = μ(s)(C) μ(l) < μ(s) (D) 不能确信6. 在恒温抽暇的玻璃罩中封入两杯液面一样的糖水 (A) 和纯水 (B)。
经历假设干时刻后,两杯液面的高度将是(μ(纯水)>μ(糖水中水) ,水从(B) 杯向(A) 杯转移 ) ( A )(A) A 杯高于 B 杯 (B) A 杯等于 B 杯(C) A 杯低于 B 杯 (D) 视温度而定7. 在通常情形下,关于二组分物系能平稳共存的最多相为: ( D )(A) 1 (B) 2 (C) 3 (D) 4 * Φ=C+2-f=2+2-0=48. 硫酸与水可形成H2SO4·H2O(s)、H2SO4·2H2O(s)、H2SO4·4H2O(s)三种水合物,问在 101325 Pa 的压力下,能与硫酸水溶液及冰平稳共存的硫酸水合物最多可有多少种? ( C )(A) 3 种 (B) 2 种(C) 1 种 (D) 不可能有硫酸水合物与之平稳共存。
物理化学 计算题

物理化学 计算题1.1mol 单原子理想气体,由298K 、5p 的始态膨胀到压力为p 的终态,经过下列途径:⑴等温可逆膨胀;⑵外压恒为p 的等温膨胀;⑶绝热可逆膨胀;⑷外压恒为p 的绝热膨胀。
计算各途经的Q 、W 、∆U 、∆H 、∆S 、∆A 与∆G 。
巳知m S (298K) = 126 J·K -1·mol -1 。
解:(1)等温过程:ΔU = ΔH = 0,J5.3987K J 38.132985.3987J 5.3987J 5.39875ln 298314.81ln 1-R 21-=∆=∆⋅===∆-==⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛=-=G A T Q S W p p nRT W Q ,;(2) ΔU = ΔH = 0,()()221118.31429810.21982J p Q W p V V RT p ⎛⎫=-=-=-=⨯⨯-= ⎪⎝⎭J 5.3987KJ 38.13ln 1-21-=∆=∆⋅=⎪⎪⎭⎫ ⎝⎛=∆A G p p nR S , (3) K 8.1565298355212112=⨯=⎪⎪⎭⎫ ⎝⎛==--γγγp p T T , ()()()()()()()J129652988.1566.1122934J143182988.1566.1121761K J 6.1125ln 126ln 2980J1761J 29342988.15625J 17612988.1562312121-2121m ,m ,=-⨯--=--∆=∆=-⨯--=--∆=∆⋅=-=⎪⎪⎭⎫ ⎝⎛-===∆-=∆=-=-⨯=∆=∆=-=-⨯=∆=∆T T S H G T T S U A R p p R K S S S S U W R T nC H Q R T nC U p V ,,,(4) ()()12212230V V p T T R W U Q --=-=∆=,,()()()()()()()()()J76612986.1126.2021181983J84542986.1126.2021181190K J 11836.56.112K J 6.112K J 36.5ln ln J19832986.20225J 19902986.20223K 6.2025129829823112211221-121-11-2112m ,12m ,12m ,222=⨯-⨯--=--∆=∆=⨯-⨯--=--∆=∆⋅=+=∆+=⋅=⋅=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=∆-=-⨯=-=∆=-=-⨯=-=∆=⎪⎭⎫ ⎝⎛⨯--=-T S T S H G T S T S U A S S S S p p nR T T nC S R T T nC H WR T T nC U T T R T R p p V ,,2.10mol H 2(理想气体),C V ,m = 5/2R J·K -1·mol -1,在298K 、p ө时绝热可逆地压缩到10p ө,计算该过程的Q 、W 、∆U 、∆H 、∆S 、∆F 和∆G 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1mol 单原子理想气体,由298K 、5p 的始态膨胀到压力为p 的终态,经过下列途径:⑴等温可逆膨胀;⑵外压恒为p 的等温膨胀;⑶绝热可逆膨胀;⑷外压恒为p 的绝热膨胀。
计算各途经的Q 、W 、∆U 、∆H 、∆S 、∆A 与∆G 。
巳知m S (298K) = 126 J·K -1·mol -1 。
解:(1)等温过程:ΔU = ΔH = 0,J5.3987K J 38.132985.3987J 5.3987J 5.39875ln 298314.81ln 1-R 21-=∆=∆⋅===∆-==⨯⨯⨯=⎪⎪⎭⎫⎝⎛=-=G A T Q S W p p nRT W Q ,;(2) ΔU = ΔH = 0,()()221118.31429810.21982Jp Q W p V V RT p ⎛⎫=-=-=-=⨯⨯-= ⎪⎝⎭J5.3987KJ 38.13ln 1-21-=∆=∆⋅=⎪⎪⎭⎫ ⎝⎛=∆A G p p nR S ,(3)K8.1565298355212112=⨯=⎪⎪⎭⎫ ⎝⎛==--γγγpp T T ,()()()()()()()J129652988.1566.1122934J143182988.1566.1121761KJ 6.1125ln 126ln 2980J1761J 29342988.156250J 17612988.1562312121-2121m ,m ,=-⨯--=--∆=∆=-⨯--=--∆=∆⋅=-=⎪⎪⎭⎫ ⎝⎛-===∆-=∆=-=-⨯=∆=∆=-=-⨯=∆=∆T T S H G T T S U A R p p R K S S S S U W R T nC H Q R T nC U p V ,,, (4)()()12212230V V p T T R W U Q --=-=∆=,,()()()()()()()()()J76612986.1126.2021181983J84542986.1126.2021181190K J 11836.56.112K J 6.112KJ 36.5ln ln J19832986.20225J 19902986.20223K 6.2025129829823112211221-121-11-2112m ,12m ,12m ,222=⨯-⨯--=--∆=∆=⨯-⨯--=--∆=∆⋅=+=∆+=⋅=⋅=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=∆-=-⨯=-=∆=-=-⨯=-=∆=⎪⎭⎫ ⎝⎛⨯--=-T S T S H G T S T S U A S S S S p p nR T T nC S R T T nC H WR T T nC U T T R T R p p V ,,2.10mol H 2(理想气体),C V ,m = 5/2R J·K -1·mol -1,在298K 、p ө时绝热可逆地压缩到10p ө,计算该过程的Q 、W 、∆U 、∆H 、∆S 、∆F 和∆G 。
巳知 m S (298K) = 130.59 J·K -1·mol -1 。
解:3.银可能受到的腐蚀而发生下列反应:H 2S(g)+2Ag(s) = Ag 2S(s)+H 2(g)今在298K 和标准压力Pθ下,将银放在等体积的氢和H 2S 组成的混合气中。
已知:298K 时,Ag 2S(s)和H 2S(g)的标准生成吉布斯自由能分别为-40.26和-33.02kJ.mol -1。
试问是否可能发生腐蚀而生成硫化银。
在混合气中,硫化氢的百分数低于多少,才不致发生腐蚀?⑴ 判断Ag 能否被腐蚀而生成Ag2S,就是判断在给定的条件下,所给的反应能否自发进行。
可以计算ΔG 值,由ΔG 的正、负来判断,也可以计算反应的平衡常数K ,再比较K与Qa 的大小来判断。
用ΔG 判断:ΔG=ΔG+RTlnQa该复相反应Qa=Qp ,Qp 为指定条件下的压力商,其值为其中摩尔分数之比等于体积百分数之比。
此时ΔG=ΔG =ΔG f, Ag2S(S)-ΔG f,H2S(g) =-40.25+32.93 =-7.32KJ/molΔG<0,故在该条件下,Ag 能被腐蚀而生成Ag2S ⑵ 若使Ag 不致被腐蚀,应使ΔG≥0,即Qa≥K 设此时H2S 的体积百分数为X,则H2的百分数为1-X 。
则Qa =(1-X )/X Qa≥K,即(1-X )/X>=19.15 解得 X≤4.96%即在混合气体中,H2S 的百分数低于4.96%时,才不致发生腐蚀。
4.在Hittorf 迁移管中,用Cu 电极电解已知浓度的CuSO 4溶液。
通电一定时间后,串联在电路中的银库仑计阴极上有0.0405 g Ag(s) 析出。
阴极区溶液质量为36.434 g ,据分析知,在通电前其中含CuSO 4 1.1276 g ,通电后含CuSO 4 1.109 g 。
试求2+Cu 和 24SO -的离子迁移数。
解法1:先求2+Cu 的迁移数,以2+Cu 为基本粒子,已知:14(CuSO )159.62 g mol M -=⋅14()0.0405 g/(2107.88 g mol ) 1.877110 mol n --=⨯⋅=⨯电13() 1.1276 g/159.62 g mol 7.064310 mol n --=⋅=⨯始 13() 1.109 g/159.62 g mol 6.947610 mol n --=⋅=⨯终阴极上2+Cu 还原,使2+Cu 浓度下降 2+Cu 2e Cu(s)-+→()()()()n n n n =+-终始迁电 5()7.1010 mol n -=⨯迁 2+()(Cu )0.38()n t n ==迁电24(SO )10.62t t -+=-= 解法2:先求2-4SO 的迁移数,以2-41SO 2为基本粒子。
阴极上2-4SO 不发生反应,电解不会使阴极区2-4SO 离子的浓度改变。
电解时2-4SO 迁向阳极,迁移使阴极区 2-4SO 减少。
((n n n =-终)(始)迁)(mol n ⨯-4求得迁)=2.33102-4((SO )0.62()n t n ==迁)电10.38t t +-=-= 解法3:如果分析的是阳极区的溶液,基本计算都相同,只是离子浓度变化的计算式不同。
(1)阳极区先计算2+Cu 的迁移数,阳极区Cu 氧化成2+Cu ,另外2+Cu 是迁出的,()()()()n n n n =+-终始电迁(2)阳极区先计算24SO -迁移数,阳极区24SO -不发生反应,24SO -迁入。
()()()n n n =+终始迁5.用银电极电解 KCl 水溶液。
电解前每 100g 溶液中含 KCl 0.7422g 。
阳极溶解下来的银与溶液中的 Cl - 反应生成 AgCl(S),其反应可表示为 Ag→Ag ++e -,Ag ++Cl -→AgCl(S),总反应为 Ag +Cl -→AgCl(S)+e -。
通电一定时间后,测得银电量计中沉积了 0.6136g Ag ,并测知阳极区溶液重 117.51g ,其中含 KCl 0.6659g 。
试计算 t (K +) 和 t (Cl -)。
解: 对于只含一种正离子和一种负离子的电解质溶液,只需求出其中任一种离子的迁移数即可。
由 Ag 电量计上析出的 Ag 计算通过电解池电荷的物质的量n =0.6136g/107.87g·mol -1=5.688x10-3mol设阳极区水的量在电解前后不变。
W水(阳极区)=(117.51-0.6659)g=116.844g电解前后Cl-的物质的量为6.电池Pt,H2( pө)|HBr(a = 1)|AgBr(s),Ag 的Eө与温度T的关系式为:Eө = 0.07150 - 4.186 × 10-7T(T- 298) 。
(1) 写出电极反应与电池反应;(2) 求T = 298K时正极φө与AgBr的K sp,巳知φө(Ag+/Ag) = 0.7991 V ;(3) 求T = 298K电池反应的平衡常数(可逆放电2F);(4) 此电池在298K下可逆放电2F时,放热还是吸热?热是多少?解:(1) 负极:H2(g)-2e →2H+;正极:2AgBr(s) + 2e →2Ag(s) + 2Br-电池反应:H2(g) + 2AgBr(s) = 2Ag(s) + 2HBr(a = 1)(2) T = 298K ,Eθ= 0.07150 Vφθ(正) =φθ(AgBr/Ag) = Eθ-φθ(H+/H2) = Eθ= 0.07150 V∵φθ(AgBr/Ag) =φθ(Ag+/Ag) + 0.05915lg K sp即0.07150 = 0.7991 + 0.05915lg K sp∴K sp = 5.0 × 10-13(3) Δr Gθm=-RT ln Kθ=-nFEθln Kө= nFEө/RT = 2 × 96500 × 0.07150/(8.314 × 298) = 5.5640,所以Kө= 2.62 × 102(4) (∂E/∂T)p=-4.186×10-7×2T + 4.186×10-7×298=-9.372×10-7T + 124.76×10-6T= 298K (∂E/∂T)p =-124.76×10-6 < 0,放热Q r = nFT(∂E/∂T)p = 2×96500×298×(-124.76×10-6) =-7175 J7.298K,pH = 5时,蔗糖转化反应有一个常数的半衰期为500分钟(即半衰期与糖的起始浓度无关),在同一温度下,当pH = 4时,常数半衰期为50分钟,试问蔗糖转化反应:A(蔗糖) + H+-→P的速率方程中,a、b值为多少?8.对峙反应D-R1R2R3CBr L-R1R2R3CBr若正逆向反应为一级反应且半衰期均为10min。
今从1.000molD-溴化物开始,试问10min后可得到L-溴化物若干?解:k1= ㏑2/t1/2=0.693/10=0.0693,因题意k1=k-1 故有㏑[a(a-(k1+k-1)/k1)x]=(k1+k-1)t代入a=1 k1=k-1=0.0693 x=0.375mol。
