物理化学计算题及答案
物理化学计算题及答案

物理化学计算题及答案第一章例4在100℃,p下,1mol水(1)可逆蒸发,(2)向真空蒸发为蒸气。
已知vapHm=40.7kJmol-1,假设蒸气为理想气体,液体水的体积可忽略不计,求Q,W,U,H。
解:(1)H=Qp=40.7kJW=-pV=-pVg=-RT=-3.1kJU=Q-W=(40.7-3.1)kJ=37.6kJ(2)始终态同(1)故H=40.7kJU=37.6kJ向真空蒸发W=0Q=U=37.6kJ例5将100g,40℃水和100g,0℃的冰在杜瓦瓶中(恒压,绝热)混合,求平衡后的状态,及此过程的H。
已知冰的熔化热=335Jg-1,Cp(水)=4.18JK-1g-1解:设水和冰为系统。
因恒压,绝热所以H=Qp=0又H=H(水)+H(冰)=0设终态温度为TH=H(水)+H(冰)=1004.18(T–313)+100335=0T=253K该结果是不可能的!100g水全部降温至0℃,放热:H(水)=–1004.1840=–16.7kJ100g 冰全部融化吸热:H(冰)=33.5kJ说明冰不能全部融化,终态应是0℃的冰水混合物。
设m克冰融化,H=H(冰)+H(水)=m0.335-16.7=0m=50g平衡后的状态为50g冰和150g水的0℃的冰水混合物。
例6已知某气体的状态方程为:UHpVpVm=RT+bp(b>0常数)TpVTpVTTpTVT请依据推导结果判断(1)在绝热自由膨胀过程中,该气体的温度如何变化(2)在绝热节流膨胀过程中,该气体的温度如何变化V2TT解:(1)绝热自由膨胀过程是等内能过程,U=0,则VVUdV所以本题要解的1是μJ的正负令U=f(T,V),根据循环关系式:UTVV1CVJTVVUUTUT1U1TpJpTVCVCTVVUTV现在只要判断[]是>0,=0,还是<0?其中的偏微商与气体的状态方程有关。
VpTJ1TppTVUCVTV焦耳系数气体的状态方程可改写为p(Vm–b)=RTRTRp其中p对T求导得:VmbTVVmbRT1代入上式:pT0VCVbUVm故温度不变分析:若把气体的状态方程p(Vm–b)=RT与理想气体的状态方程pVm=RT比较,有什么结论可看出该方程只修正了气体分子的体积(Vm–b),而分子间作用力这一项没有修正,说明p=p理气,故在绝热自由膨胀过程中温度没有变化。
物理化学习题-含答案
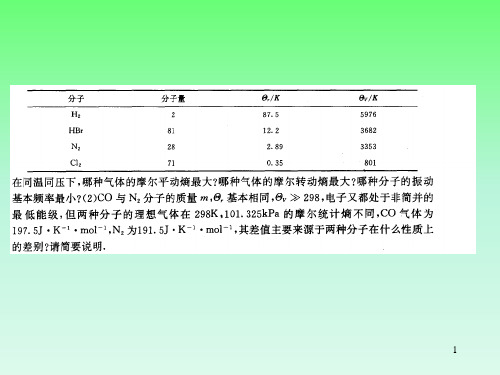
基态是单态。计算在298K、1atm下一氧化碳气体的 摩尔熵值。
7
解:由于CO气体为非定位体系,其熵公式为:
ln Q Q NkT S k ln N! T
N
ln Q Nk ln Q k ln N! NkT T
可将其看成是体系的平动熵、转动熵、振动熵及电子熵等之 和。可先分别求出各运动形式的熵、再求和而得体系的总熵 。上式的-k lnN! 项归入平动熵计算。
32
将题中给出的数据直接代入上式得:
Q转
2 8 1.1461045 1.381023 298 (3.1416 )
2 (6.62610
34 2
)
424
5
(3)如果将分子看成是谐振子,则有
Q振 1 1 e h kT 1 1 e h c kT
由题意知,
565cm1 565102 m1
~
1 代入上式得: Q振 6.6261034 565102 2.998108 1 exp[ ] 23 1.3810 298
1
1 e
2.73
1.07
6
计算题
2.已知一氧化碳分子的转动惯量是
I 1.451046 kg m2 ~ 1 基本振动波数 2170cm ,分子量为 28.0,其电子
2170cm1 217000 m1
ln Q h c e h c kT T kT2 1 e h c kT
12
将数据代入得
ln Q振 T
计算题
10.5 e10.5 0 10.5 298 (1 e )
S振 R ln Q振 RT T 8.314 ln 1 8.314 298 0 0
物理化学试题及答案

物理化学试题及答案一、选择题(每题2分,共20分)1. 物质的量浓度为0.5 mol/L的溶液中,含有多少摩尔的溶质?A. 0.5 molB. 1 molC. 2 molD. 无法确定2. 根据热力学第一定律,下列哪项描述是错误的?A. 能量守恒B. 能量可以无限制地从低温物体传向高温物体C. 能量可以转化为其他形式D. 能量在转化过程中总量保持不变3. 以下哪个不是热力学基本定律?A. 能量守恒定律B. 熵增原理C. 热力学第三定律D. 牛顿第二定律4. 理想气体状态方程是:A. PV = nRTB. PV = P0V0C. P1V1/T1 = P2V2/T2D. P1V1 = P2V25. 根据范特霍夫方程,当温度升高时,化学平衡会向哪个方向移动?A. 正反应方向B. 逆反应方向C. 不变D. 无法确定6. 反应速率常数k与温度T的关系遵循:A. 阿累尼乌斯方程B. 范特霍夫方程C. 理想气体状态方程D. 热力学第一定律7. 以下哪个是化学动力学的基本概念?A. 反应热B. 活化能C. 熵变D. 吉布斯自由能8. 电化学中,阳极发生的反应是:A. 氧化反应B. 还原反应C. 酸碱中和反应D. 沉淀反应9. 根据吉布斯自由能变化,一个反应在恒温恒压下自发进行的条件是:A. ΔG > 0B. ΔG < 0C. ΔG = 0D. ΔG ≠ 010. 表面张力是液体表面分子间作用力的体现,它会导致液体表面:A. 收缩B. 膨胀C. 保持不变D. 无法确定二、填空题(每空2分,共20分)11. 物质的量浓度C= _______ 。
12. 热力学第一定律的数学表达式为 _______ 。
13. 理想气体状态方程的变量不包括 _______ 。
14. 阿累尼乌斯方程的数学表达式为 _______ 。
15. 电化学中,阴极发生的反应是 _______ 。
16. 吉布斯自由能变化的数学表达式为 _______ 。
物理化学期末考题(四,计算题参考答案)

仅供参考,请勿外传计算题参考答案1.1mol 单原子理想气体的始态为300K ,500kPa 。
(1)在等温条件下向真空膨胀至100kPa ,求此过程的Q 、W 、U ∆、H ∆、S ∆、A ∆、G ∆。
(2)在恒压条件下,体积增至原来的两倍(V 2=2V 1), 求此过程的Q 、W 、U ∆、H ∆、S ∆。
解:(1) 因为向真空膨胀,等温过程,故:01=Q ,01=W ,01=∆U ,01=∆HJ 4014kPa500kPa100ln K 300K mol J 8.314mol 1ln111211-=⨯⨯⋅⋅⨯==∆=∆--p p nRT G A 111211K J 38.13kPa100kPa 500ln K mol J 8.314mol 1ln---⋅=⨯⋅⋅⨯==∆p p nR S (2) 因为12212,V V p p ==,所以,由111222T V p T V p =,得K 600212==T T J 6236K 300)(600K m o l J 8.31425m o l 1)(1112m ,22=-⨯⋅⋅⨯⨯=-==∆--T T nC Q H p J 3741K 300)(600K m o l J 8.31423m o l 1)(1112m ,2=-⨯⋅⋅⨯⨯=-=∆--T T nC U V J 2495J 6236J 3741222-=-=-∆=Q U W1K600K300m,m ,2K J 4.14K300K600ln 8.314251d 1d 21-⋅=⨯⨯=⨯==∆⎰⎰T TC T TnC S p T T p2.1mol 理想气体,始态压力202650Pa ,体积为22.4dm 3,连续经历下列三个过程达到终态。
(1) 从始态可逆膨胀至B ,其压力为101325Pa ;(2)从B 再等容加热至C ,其温度为1091.9K ; (3)从C 再在等压条件下冷却至终态D ,其温度为545.9K 。
物理化学考试题及答案

物理化学考试题及答案一、选择题1. 在标准状况下,1摩尔理想气体的体积为:A. 22.4 LB. 22.0 LC. 24.4 LD. 23.9 L答案:A2. 根据热力学第一定律,一个系统吸收的热量等于:A. 系统的内能增加量B. 系统对外做功的负值C. 系统对外做功的正值加上内能增加量D. 系统的熵变答案:C3. 电解质溶液的电导率主要取决于:A. 溶液的温度B. 溶液的浓度C. 溶质的化学性质D. 所有以上因素答案:D4. 表面张力的作用是:A. 增加液体的表面积B. 减少液体的表面积C. 使液体表面形成平面D. 使液体表面形成球面答案:B5. 阿伏伽德罗定律表明,在相同的温度和压力下,等体积的气体含有相同数量的:A. 分子B. 原子C. 电子D. 质子答案:A二、填空题1. 在化学反应中,当一个系统达到平衡状态时,正反应速率与逆反应速率相等,此时系统的________和________不变。
答案:温度;压力2. 物质的量浓度(C)定义为溶液中溶质的________与溶液的________之比。
答案:物质的量;体积3. 根据热力学第二定律,自然系统中的熵总是倾向于增加,这意味着能量会从________向________转移。
答案:高能级;低能级4. 布朗运动是指悬浮在液体中的微小颗粒由于液体分子的________作用而表现出的无规则运动。
答案:碰撞5. 电化学电池的工作基于________原理,通过氧化还原反应将化学能转换为电能。
答案:氧化还原三、简答题1. 请简述热力学第一定律的含义及其在物理化学中的应用。
答案:热力学第一定律,也称为能量守恒定律,表明能量既不能被创造也不能被消灭,只能从一种形式转换为另一种形式。
在物理化学中,这一定律用于描述化学反应或物理过程中能量的转换和守恒,例如在燃烧反应中化学能转换为热能和光能,或在电池中化学能转换为电能。
2. 解释表面张力的形成原因及其对液体表面的影响。
物理化学试卷及答案3套

三、计算题( 共5题60分)21. 10 分(0824)计算1mol He(理想气体) 在下列状态变化过程中的ΔH和ΔG。
He (101.325 kPa,473 K)−−→He (101.325 kPa,673 K)已知:C p, m [He(g)] = (5/2)R,473K 时S m[He(g)] = 135.1 J·K-1·mol-1。
22. 15 分(1104)某气体状态方程为pV = n(RT + Bp),始态为p1T1,该气体经绝热真空膨胀后终态压力为p2,试求该过程的Q,W及气体的ΔU,ΔH,ΔF,ΔG,ΔS。
23. 10 分(1809)两液体A, B形成理想液体混合物。
在320 K,溶液I含3 mol A和1 mol B,总蒸气压为:5.33×104 Pa。
再加入2 mol B 形成理想液体混合物II,总蒸气压为6.13×104 Pa。
(1) 计算纯液体的蒸气压p A*,p B*;(2) 理想液体混合物I的平衡气相组成y B;(3) 理想液体混合物I的混合过程自由能变化Δmix G m;(4) 若在理想液体混合物II中加入3 mol B形成理想液体混合物Ⅲ,总蒸气压为多少?24. 15 分(2419)固体CO2的蒸气压与温度间的经验式为:ln(p/Pa)=-3116 K/T + 27.537已知熔化焓∆fus H m= 8326 J·mol-1,三相点的温度为217 K。
试求出液体CO2的蒸气压与温度的经验关系式。
25. 10 分(2965)3H2+ N2= 2NH3在350℃的K p= 6.818×10-8(kPa)-2,并设与压力无关,从3:1的H2,N2混合物出发,在350℃下要获得物质的量分数为0.08 的NH3,压力至少要多大?26. 13 分(0957)4 g Ar(可视为理想气体,其摩尔质量M(Ar)=39.95 g·mol-1)在300 K时,压力为506.6 kPa,今在等温下反抗202.6 kPa的恒定外压进行膨胀。
物理化学考研题库计算题及答案
物理化学考研题库计算题及答案物理化学考研题库计算题及答案在物理化学的考研中,计算题占据了很大的比重。
掌握好计算题的解题方法和技巧,对于提高分数至关重要。
本文将介绍一些常见的物理化学考研计算题及其解答方法,希望对考生有所帮助。
一、热力学计算题1. 根据给定的反应热和反应物的摩尔数,计算反应物的标准摩尔焓变。
解答方法:根据反应热的定义,可以得到反应物的标准摩尔焓变公式为ΔH = ΔH反应/反应物的摩尔数。
根据题目给出的数据,代入公式中即可计算出反应物的标准摩尔焓变。
2. 根据给定的物质的热容和温度变化,计算物质的热量变化。
解答方法:根据热容的定义,可以得到物质的热量变化公式为Q = mCΔT,其中Q为热量变化,m为物质的质量,C为物质的热容,ΔT为温度变化。
根据题目给出的数据,代入公式中即可计算出物质的热量变化。
二、量子化学计算题1. 根据给定的波长和速度,计算光的频率。
解答方法:根据光的速度公式v = λf,其中v为光的速度,λ为光的波长,f为光的频率。
根据题目给出的数据,代入公式中即可计算出光的频率。
2. 根据给定的电子的能级差和普朗克常数,计算电子的能量。
解答方法:根据能量和频率的关系E = hf,其中E为能量,h为普朗克常数,f 为频率。
根据题目给出的数据,代入公式中即可计算出电子的能量。
三、动力学计算题1. 根据给定的反应速率常数和反应物的浓度,计算反应速率。
解答方法:根据反应速率的定义v = k[A],其中v为反应速率,k为反应速率常数,[A]为反应物的浓度。
根据题目给出的数据,代入公式中即可计算出反应速率。
2. 根据给定的反应速率和反应物的浓度,计算反应速率常数。
解答方法:根据反应速率的定义v = k[A],可以得到反应速率常数公式为k = v/[A]。
根据题目给出的数据,代入公式中即可计算出反应速率常数。
以上是物理化学考研中常见的计算题及其解答方法。
在解题过程中,注意理清思路,将题目所给的数据代入相应的公式中,正确计算出结果。
物理化学考研考试题及答案
物理化学考研考试题及答案### 物理化学考研考试题及答案#### 一、选择题(每题2分,共20分)1. 热力学第一定律的数学表达式是:A. ΔU = Q - WB. ΔH = Q + WC. ΔS = Q/TD. ΔG = ΔH - TΔS2. 根据范特霍夫方程,反应的平衡常数K随温度变化的表达式是:A. dlnK/dT = ΔH/RB. dlnK/dT = ΔS/RC. dlnK/dT = -ΔH/RT^2D. dlnK/dT = -ΔS/RT^23. 以下哪个是理想气体状态方程?A. PV = nRTB. PV = nRT + aC. PV = nRT - aD. PV = nR(T + a)4. 阿伏伽德罗定律适用于:A. 所有气体B. 理想气体C. 固体和液体D. 所有物质5. 根据吉布斯自由能的定义,下列哪个表达式是正确的?A. ΔG = ΔH - TΔSB. ΔG = ΔU + PΔVC. ΔG= ΔU - TΔSD. ΔG = ΔH - PΔV6. 反应速率常数k与温度T的关系遵循:A. 阿累尼乌斯方程B. 范特霍夫方程C. 阿伏伽德罗定律D. 理想气体状态方程7. 以下哪个是热力学第二定律的表述?A. 能量守恒B. 热量不能自发地从低温物体传向高温物体C. 没有永动机D. 所有自发过程都伴随着熵的增加8. 根据化学平衡常数的定义,下列哪个表达式是正确的?A. K = [A][B]/[C][D]B. K = [C][D]/[A][B]C. K = [A]/[B]D. K = [B]/[A]9. 以下哪个是溶液的拉乌尔定律?A. P = XA * PAB. P = (XA * PA) + (XB * PB)C. P = (PA + PB) / 2D. P = (PA * PB)^0.510. 根据亨利定律,下列哪个表达式是正确的?A. P = kH * CB. P = kH * C^2C. P = kH / CD. P = kH * C^-1#### 二、简答题(每题10分,共30分)1. 简述热力学第二定律的两种表述方式,并说明它们之间的联系。
大学物理化学试题及答案
物理化学试卷一一、选择题共15题 30分1. 下列诸过程可应用公式 dU = Cp- nRdT进行计算的是: CA 实际气体等压可逆冷却B 恒容搅拌某液体以升高温度C 理想气体绝热可逆膨胀D 量热弹中的燃烧过程2. 理想气体经可逆与不可逆两种绝热过程: BA 可以从同一始态出发达到同一终态因为绝热可逆ΔS = 0B 从同一始态出发,不可能达到同一终态绝热不可逆 S > 0C 不能断定 A、B 中哪一种正确所以状态函数 S 不同D 可以达到同一终态,视绝热膨胀还是绝热压缩而定故终态不能相同3. 理想气体等温过程的ΔF; CA>ΔG B <ΔG C =ΔG D 不能确定4. 下列函数中为强度性质的是: CA SB G/ pTC U/ VT 容量性质除以容量性质为强度性质D CV5. 273 K,10p 下,液态水和固态水即冰的化学势分别为μl 和μs,两者的关系为: CA μl >μsB μl = μsC μl < μsD 不能确定6. 在恒温抽空的玻璃罩中封入两杯液面相同的糖水 A 和纯水 B;经历若干时间后,两杯液面的高度将是μ纯水>μ糖水中水 ,水从B 杯向A 杯转移 AA A 杯高于B 杯 B A 杯等于 B 杯C A 杯低于 B 杯D 视温度而定7. 在通常情况下,对于二组分物系能平衡共存的最多相为: DA 1B 2C 3D 4 Φ=C+2-f=2+2-0=48. 硫酸与水可形成H2SO4·H2Os、H2SO4·2H2Os、H2SO4·4H2Os三种水合物,问在 101325 Pa 的压力下,能与硫酸水溶液及冰平衡共存的硫酸水合物最多可有多少种 CA 3 种B 2 种C 1 种D 不可能有硫酸水合物与之平衡共存;S = 5 , R = 3 , R' = 0,C= 5 - 3 = 2f= 2 -Φ+ 1 = 0, 最大的Φ= 3 , 除去硫酸水溶液与冰还可有一种硫酸水含物与之共存;9. 已知 A 和 B 可构成固溶体,在 A 中,若加入 B 可使 A 的熔点提高,则B在此固溶体中的含量必 _______ B 在液相中的含量; AA 大于B 小于C 等于 D不能确定10. 已知反应 2NH3= N2+ 3H2在等温条件下,标准平衡常数为 0.25,那么,在此条件下,氨的合成反应 1/2 N2+3/2 H2= NH3 的标准平衡常数为: CA 4B 0.5C 2 KD 1$p2 = K $p1 = 0.25 = 211. 若 298 K 时,反应 N2O4g = 2NO2g 的 K $p= 0.1132,则:1 当 p N2O4 = p NO2 = 1 kPa 时,反应将 _____ B _____;2 当 p N2O4 = 10 kPa,p NO2 = 1 kPa 时,反应将 ____ A ____ ;A 向生成 NO2的方向进行B 向生成 N2O4的方向进行C 正好达化学平衡状态D 难于判断其进行方向12. 在一定温度和压力下,对于一个化学反应,能用以判断其反应方向的是 CA ΔrG $mB KpC ΔrGmD ΔrHm13. 1 处于标准态的 CO2g 和 O2 g,其标准燃烧焓值为零2 因为ΔrG $m= -RT lnK $p,而K $p是由平衡时的组成表示的,所以ΔrG $m表示平衡时产物的吉布斯自由能与反应物的吉布斯自由能之差3 水在25℃, p 下蒸发,求算熵变的公式为ΔS $m=ΔH $m -ΔG $m/ T4 在恒温,恒压下可逆电池反应,求算熵变的公式为ΔrSm= ΔrHm/ T上述说法正确的是: CA 1 , 2B 2 , 3C 1 , 3D 3 , 414. 在 T,p 时,理想气体反应 C2H6g = H2g + C2H4g的 Kc/Kx为: DA RTB 1/RTC RT/pD p/RT15. 标准态的选择对下列物理量有影响的是: CA f, ,ΔrG $mB m, ,ΔF$mC a, ,ΔrGD a, , G/ T,p,wf 0二、填空题共 5题 10分16. 某理想气体,等温25℃可逆地从1.5 dm3膨胀到10 dm3时,吸热9414.5 J,则此气体的物质的量为 Q=W=nRTlnV2/V1,n=2 mol 摩尔;17. 化学位μB就是 B 物质的偏摩尔吉布斯自由能 ;18. N2g,O2g 体系中加入一种固体催化剂,可生成几种气态氮的氧化物,则体系的自由度为 f = 3 ;19. 完全互溶的二组分溶液,在x B= 0.6 处平衡蒸气压有最高值,那么组成x B=0.4的溶液在气-液平衡时,xBg,xBl,xB总的大小顺序为__ xBg > xB总 > xBl _ ;将xB=0.4 的溶液进行精镏,塔顶将得到 _ xB= 0.6 恒沸混合物 ;20. 低压气相反应的平衡常数与温度,压力的关系分别是:Kp只是温度的函数, Kc是 _T___的函数,Kx是 _ T, p __ 的函数;三、计算题共 5题 60分21. 计算 1mol He理想气体在下列状态变化过程中的ΔH和ΔG;He 101 325 kPa,673 K He 101 325 kPa,473 K 已知:Cp, m Heg = 5/2R ,473K 时 S $mHeg = 135.1 J·K-1·mol-1 ;答ΔH = T2T1nCp,m dT = 4.157 kJ 2分ΔS = T2Cp,m /TdT = nCp,m lnT2/T1= 7.3 J·K-1 4分S2= ΔS + S1= 142.4 J·K-1 2分ΔG =ΔH -ΔTS = ΔH - T2S2+ T1S1= 27.780 kJ22.某气体状态方程为 pV = nRT + Bp,始态为p1T1,该气体经绝热真空膨胀后终态压力为p2,试求该过程的Q,W及气体的ΔU,ΔH,ΔF,ΔG,ΔS;答Q = 0 , W = 0 , ΔU = 0 3分U/ VT = T p/ TV -p = 0 dU = CVdT + U/ VTdV = CVdT = 0 温度不变ΔH =ΔU +ΔpV = nBp2- p1 5分p2T1n ΔSySS = V/ Tpdp = nRlnp1/p2ΔsurrS = -Q/T = 0 ΔisoS = nRlnp1/p2 3分ΔF =ΔU-TΔS = -nRT1lnp1/p2 2分ΔG =ΔH-TΔS = nBp2-p1-nRT1lnp1/p223. 10 分 1809两液体A, B形成理想液体混合物;在320 K,溶液I含3 mol A和1 mol B,总蒸气压为:5.33×104 Pa;再加入2 mol B 形成理想液体混合物II,总蒸气压为6.13×104 Pa;1 计算纯液体的蒸气压 p A,pB;2 理想液体混合物I的平衡气相组成 yB;3 理想液体混合物I的混合过程自由能变化ΔmixGm;4 若在理想液体混合物II中加入3 mol B形成理想液体混合物Ⅲ,总蒸气压为多少答 a p = pAxA+ pBxB5.33×104 Pa = 0.75 pA+ 0.25 pB ------------- 16.13×104 Pa = 0.5 pA+ 0.5 pB ------------- 2联立 1 式与 2 式得:pA= 4.53×104 Pa pB= 7.73×104 Pa 2.5分 b yBI=pBxBI/pI = 0.36 2.5分 p1 c mixGmI RT nBBlnxB = -5984 J·mol 2.5分d pⅢ=pAxAⅢ +pBxBⅢ= 6.66×104 Pa 2.5分24.固体 CO2的蒸气压与温度间的经验式为:lnp/Pa=-3116 K/T + 27.537已知熔化焓fusHm= 8326 J·mol-1,三相点的温度为 217 K;试求出液体 CO2的蒸气压与温度的经验关系式;答:已知 lnp/Pa = -3116 K/T + 27.537对固气平衡:dlnp/Pa/dT =ΔsubHm/RT2dlnp/Pa/dT = 3116 K/T2=ΔsubHm/RT2ΔsubHm= 25 906 J·mol-1 4分ΔvapHm=ΔsubHm-ΔfusHm= 17 580 J·mol-1 4分-ΔvapHm/RT + B = -3116 K/T + 27.537 B = 22.922 4分所以液体 CO2的蒸气压与温度的经验关系为: lnp/Pa = -ΔvapHm/RT + 22.922 = -2115 K/T + 22.922 3分25. 3H2+ N2= 2NH3在350℃的Kp= 6.818×10-8kPa-2,并设与压力无关,从3:1的 H2,N2混合物出发,在350℃下要获得物质的量分数为 0.08 的 NH3,压力至少要多大答 3H2g + N2g = 2NH3g 2分平衡时:3 mol-3n 1 mol-n 2nB= 4 mol- 2n 1分 2n/4 mol-2n = 0.08 n = 0.148 mol 2分故 xH2 = 0.69 xN2 = 0.23 2分Kp =xNH3p2/xH2p3xN2p= 6.818×10-8 kPa2解得 p = 1115 kPa 3分 nB试卷二一、选择题每题2分,共50分,将唯一的答案填进括号内1. 下列公式中只适用于理想气体的是. BA. ΔU=QVB. W=nRTlnp2/p1C. ΔU=2. ΔH是体系的什么. CA. 反应热B. 吸收的热量C. 焓的变化D. 生成热3. 2000K时反应COg+1/2O2g=CO2g的Kp为6.443,则在同温度下反应为2CO2g=2COg+O2g的Kp应为. CA. 1/6.443B. 6.443C. 1/6.443D. 1/6.4434. 固态的NH4HS放入一抽空的容器中,并达到化学平衡,其组分数、独立组分数、相数及自由度分别是 . CA. 1,1,1,2B. 1,1,3,0C. 3,1,2,1D. 3,2,2,25.下列各量称做化学势的是 .D 1/221/22 TT1CV,mdT D. ΔH=ΔU+pΔVp US,V,nj iT,V,nj iT,p,nj iS,V,nj i A. ni B. ni C. ni D. ni6. A和B能形成理想溶液;已知在100℃时纯液体A的饱和蒸汽压为133.3kPa, 纯液体B的饱和蒸汽压为66.7 kPa, 当A和B的二元溶液中A的摩尔分数为0.5时,与溶液平衡的蒸气中A的摩尔分数是.CA. 1B. 0.75C. 0.667D. 0.57. 理想气体的真空自由膨胀,哪个函数不变 DA. ΔS=0B. V=0C. ΔG=0D. ΔH=08. A、B两组分的气液平衡T-x图上,有一最低恒沸点,恒沸物组成为xA=0.7;现有一组成为xA=0.5的AB液体混合物,将其精馏可得到 ;BA. 纯A和恒沸混合物B. 纯B和恒沸混合物C. 只得恒沸混合物D. 得纯A和纯B9. 实验测得浓度为0.200mol·dm-3的HAc溶液的电导率为0.07138S·m-1,该溶液的摩尔电导率ΛmHAc为 .BA. 0.3569S·m·molB. 0.0003569S·m·molC. 356.9S·m·molD. 0.01428S·m·mol10. 表面活性物质溶于水时,关于溶液的表面张力和溶液表面的描述正确的是 .DA. 表面张力升高,正吸附B. 表面张力降低,正吸附C. 表面张力升高,负吸附D. 表面张力显着降低,正吸附11. 一体积的氢气在0℃,101.3kPa下等温膨胀至原来体积的3倍,其内能变化是多少设氢气是理想气体.BA. 0.4JB. 0C. 6J12. 已知反应COg+1/2O2g=CO2g的ΔH,下列说法中何者不正确;AA. ΔH是CO2g的生成热B. ΔH是COg的燃烧热C. ΔH是负值D. ΔH与反应ΔU的数值不等13. 对于0.002mol/kg的Na2SO4溶液,其平均质量摩尔浓度m±=0.219是 AA. 3.175×10B. 2.828×10C. 1.789×10D. 4×1014. 对弯曲液面所产生的附加压力.BA. 一定等于零B. 一定不等于零C. 一定大于零D. 一定小于零15. 已知下列反应的平衡常数: .AH2g + Ss = H2Sg K1Ss + O2g = SO2g K2则反应H2Sg + O2g= H2g + SO2g 的平衡常数为A. K2/K1B. K1—K2C. K1×K2D. K1/K216. 对于N2和H2混合气体的绝热可逆压缩没有生产NH3,则 .CA. ΔU=0B. ΔH=0C. ΔS=0D. ΔG=017. 温度升高溶胶的稳定性.BA. 增加B. 下降C. 不变D. 先增加后下降18. 101℃时,水在多大外压下沸腾 . CA. 101.3kPaB. 1013kPaC. 略高于101.3kPaD. 略低于101.3kPa19. 在HAc电离常数测定实验中,直接测定的物理量是不同浓度的HAc溶液的BA. 电导率B. 电阻C. 摩尔电导D. 电离度20. 定温下气相反应Kp有什么特点 . AA. 恒为常数B. 恒等于KcC. 随压力而变D. 与体积有关21. 某化学反应其反应物消耗8/7所需的时间是它消耗掉4/3所需的时间的1.5倍,则反应的级数为 .BA. 零级反应B. 一级反应C. 二级反应D. 三级反应22. 在一定量AgI溶胶中加入下列不同电解质溶液,则使溶胶在一定时间内完全聚沉所需电解质的量最少的是 . BA. LaNO33B. MgNO32C. NaNO3D. KNO323. 接触角可确定固体某种性质,若亲液固体表面能被液体润湿,其相应的接触角是. CA.0B.90C.90D.为任意角24. 混合等体积0.08mol·dmKI和0.1mol·dmAgNO3溶液得到一溶胶体系,在该体系中分别加入下述三个电解质:1 MgSO4, 2 CaCl2, 3 Na2SO4, 则其聚沉能力的大小为CA.1>2>3B.2>1>3C.3>1>2D.3>2>125. 298K时反应Zn+Fe2+=Zn2++Fe的E0为0.323V,则其平衡常数为BA. 2.89×105B. 8.34×1010C. 5.53×104D. 2.35×102二、计算题:共50分1. 10分 A熔点651℃和B熔点419℃的相图具有一个低共熔点,为368℃42% A,质量百分数,下同;1 绘出该二组分系统的示意相图,标出各相区相态,及自由度;2分别指出80% A和30% A的系统从700℃冷却到300℃的过程的相变;3 画出49% A的溶液的步冷曲线;3 3单相区为Bs+l2、20分某抗菌素施于人体后在血液中的反应呈现一级反应;如在人体中注射0.5克某抗菌素,然后在不同时间测其在血液中的浓度,得到下列数据:t h CA 血液中药含量mg/100ml4 0.488 0.3112 0.2416 0.15lncA-t的直线斜率为-0.0979, lncA,0=-0.14;1 求反应速率常数;2 计算半衰期3若使血液中某抗菌素浓度不低于0.37mg/100ml,问需几小时后注射第二针;解:设cA,0为抗菌素开始浓度ln1反应速率方程积分形式 -k=-0.0979 .k=0.0979h-12cA,0cA ktlncA=-kt+lncA,0 斜率为t1 ln2k=7.08h3t=0时,ln cA= ln cA,0=-0.14lnt=1/kcA,0cA=1/0.0979ln0.72/0.37=6.8h约需6.8小时后注射第二针;3、20分 5mol过冷水在-5℃, 101.3kPa下凝结为冰,计算过程的ΔG, 并判断过程在此条件下能否发生;已知水在0℃, 101.3kPa下凝固热ΔHm,凝=-6.009J·K-1·mol-1,水的平均热容为75.3 J·K-1·mol-1, 冰的平均热容为37.6 J·K-1·mol-1;解: H2Ol H2Os n=5.00mol, n=5.00mol, t1= -5℃ t1= -5℃ p=101.3kPap=101.325kPaΔG1ΔG3H2Ol H2Os n=5.00mol, Δ G 3 n=5.00mol, t1= 0℃ t1=0℃ P=101.3kPap=101.3kPa ΔH=ΔH1+ΔH2+ΔH3=1883-30045-940=-29102J, ΔS1=nCp,m,水lnT1/T2=5×·K, ΔS2=ΔHm,凝/T=5×-6009×10/273.2=-110.0 J·KΔS3=nCp,m,冰lnT2/T1=5×·K,ΔS=ΔS1+ΔS2+ΔS3=6.95-110.0-3.47=-106.5 J·KΔG=ΔH-TΔS=-29102-268.2×-106.5=-539 J<0 w=0,等温,等压,ΔG〈 0,水可以自动结冰;试卷三一、判断题;判断下列说法的正误,在正确的说法后面打“√”,错误的说法后面打“×”;1、温度一定的时候,气体的体积与压力的乘积等于常数; x2、热力学过程中W的值应由具体过程决定√3、系统的混乱度增加,则其熵值减小; x4、处于标准状态的CO g,其标准燃烧热为零;x5、1mol理想气体从同一始态经过不同的循环途径后回到初始状态,其热力学能不变; √6、吉布斯判据适用于理想气体的任意过程; x7、四个热力学基本方程适用于所有封闭体系的可逆过程; √8、在纯溶剂中加入少量不挥发的溶质后形成的稀溶液沸点将升高; √9、惰性组分的加入将使反应的平衡转化率降低; x10、只受温度影响的平衡系统自由度F=C-P+1; √二、选择题1. 一定压力下,当2 L理想气体从0℃升温到273℃时,其体积变为 b ;A. 5 LB. 4 LC. 6 LD. 1 L2、A、B两种理想气体的混合物总压力为100kPa,其中气体A的摩尔分数0.6,则气体B的分压为 c ;A. 100kPaB. 60kPaC. 40kPaD. 不确定3、当实际气体的压缩因子Z大于1的时候表明该气体 b ;A. 易于压缩B. 不易压缩C. 易于液化D. 不易液化4、如图,将CuSO4水溶液置于绝热箱中,插入两个铜电极,以蓄电池为电源进行电解,可以看作封闭体系的是 a ;A. 绝热箱中所有物质B. 两个铜电极C. 蓄电池和铜电极D. CuSO4水溶液5、在体系温度恒定的变化中,体系与环境之间 c ;A. 一定产生热交换B. 一定不产生热交换C. 不一定产生热交换D. 温度恒定与热交换无关6、下列定义式中,表达正确的是 b ;A. G=H+TSB. G=A+PVC. A=U+TSD. H=U—PV7、在一个绝热钢瓶中,发生一个放热的分子数增加的化学反应,那么 c ;A. Q > 0,W > 0,ΔU > 0B. ΔQ = 0,W = 0,ΔU < 0C. Q = 0,W = 0,ΔU = 0D. Q < 0,W > 0,ΔU < 08、ΔH =Qp , 此式适用于下列哪个过程: b ;A. 理想气体从106 Pa反抗恒外压105 Pa膨胀到105 PaB. 0℃ , 105 Pa 下冰融化成水C. 电解 CuSO4水溶液D. 气体从 298 K, 105 Pa 可逆变化到 373 K, 104 Pa9、下述说法中,哪一种不正确: a ;A. 焓是体系能与环境进行交换的能量B. 焓是人为定义的一种具有能量量纲的热力学量C. 焓是体系状态函数D. 焓只有在某些特定条件下,才与体系吸热相等10、凝固热在数值上与下列哪一种热相等: d ;A. 升华热B. 溶解热C. 汽化热D. 熔化热11、在100℃ 和25℃ 之间工作的热机,其最大效率为 d ;A. 100 %B. 75 %C. 25 %D. 20 %12、在等压下,进行一个反应 A + B=C,若ΔrHm > 0,则该反应一定是:d ;A. 吸热反应B. 放热反应C. 温度升高D. 无法确定13、将1mol H2Ol100℃、101.325kPa置于密闭真空容器中,蒸发为同温同压的水蒸气并达平衡,该过程的△G b ;A.大于0B.小于0C.等于0D.不能确定14、1mol双原子理想气体的Cp是: c ;A. 1.5RB. 2.5RC. 3.5RD. 2R15、 2mol理想气体B在300K时等温膨胀,W =0时体积增加一倍,则其SJ·K为d ;A. -5.76B. 331C. 5.76D. 11.52三、填空题:以下各题,请将正确的答案填在空白处;1、已知稀溶液中溶质的摩尔分数为0.03,纯溶剂的饱和蒸汽压为91.3kPa,则该溶液中溶剂的蒸汽压为 88.561 kPa;2、化学式的定义式为μB=3、已知下列反应的平衡常数:H2g + Ss = H2Ss为K1 ;Ss + O2g = SO2g为K2 ;则反应 H2g + SO2g = O2g + H2Sg的平衡常数为__ K1/K2 ;4、NH4HSs放入真空容器中,并与其分解产物NH3g和H2Sg达到平衡,则该系统中组分数K= 2 ;相数Ф= 2 ;自由度F= 2 ;5、A及B二组分组成的凝聚体系能生成三种稳定的化合物,则于常压下在液相开始冷却的过程中,最多有 2 种固相同时析出四、计算题;1小题6分,2、3小题各12分,共30分1、在一定压力p和温度298.2 K的条件下,1molC2H5OHl完全燃烧时所做的功是多少设体系中气体服从理想气体行为;解:反应方程C2H5OHl + 3O2g 2CO2g+H2Ol这是等温、等压下的化学反应:W=-pV2-V1=n1RT3RTnRT2RT V2 2 pppp2RT3RTW p 2 3 RTppRT 8.314 298.2 2479JV12、101325Pa下将一盛有100℃、1mol的密闭玻璃球放在100dm3的容器中,整个容器放在100℃的恒温槽内;将玻璃小球击破,水即发生气化设蒸气为理想气体,计算该过程的Q,W, U, H, S, A,和 G;已知100℃水的气化热为40.59 kJ·mol–1;解:首先判断水是否全部气化,在101325Pa下,1mol水全部气化应占体积:V 8.315 373.153 m 30.62 dm3101325或在恒容下,1mol水全部气化后的压力:p 8.315 373.15 Pa 31025.7 Pa100 10 32分体积和压力均小于始态,表明能全部气化,末态压力应为31025.7Pa选择整个容器为系统,设计下过程理想气体恒温过程 H2=0, U2=0H= H1+ H2= H1=40.59 kJ 2分 U= U1+ U2= U1= H1– pV=H1–RT=37.47 kJ 2分因对整个容器系统 V=0,故W=0,Q= U = 37.47 kJ 2分S= S1+ S2= H1/T –nRlnp2/p1 =118.60 J·K–1 2分 A= U –T S=37.49kJ –118.60 373.15 J = –6.771 kJ 1分G= H –T S=40.59kJ –118.60 373.15 J = –3.672 kJ 1分3、已知甲苯的摩尔质量为 92 10-3 kg·mol-1,沸点为383.15K,平均摩尔气化焓为33.84kJ·mol-1;苯的摩尔质量为 78 10-3 kg·mol-1,沸点为353.15K,平均摩尔气化焓为30.03kJ·mol-1;有一含苯 100g 和甲苯 200g 的理想液态混合物,在373.15K,101.325 kPa下达气液平衡;求1373.15K 时苯和甲苯的饱和蒸气压;2平衡时液相和气相的组成;3由两组分物质形成该理想液态混合物时的混合焓和混合熵;2分 2分2分 2分。
物理化学期末试题及答案
物理化学期末试题及答案一、选择题(每题2分,共20分)1. 下列哪种物质的摩尔质量不是以克/摩尔为单位?A. 氧气B. 二氧化碳C. 氢气D. 氮气答案:C2. 在理想气体状态方程中,PV=nRT中,P代表的是:A. 压力B. 体积C. 温度D. 摩尔数答案:A3. 根据热力学第一定律,下列哪项描述是正确的?A. 能量守恒B. 能量可以被创造或消失C. 能量可以被转化为质量D. 能量可以在不同形式间转换答案:D4. 以下哪个选项是正确的?A. 温度是热力学系统的宏观量B. 温度是热力学系统的微观量C. 温度是热力学系统的微观量和宏观量D. 温度不是热力学系统的量答案:A5. 根据热力学第二定律,下列哪项描述是错误的?A. 热量不能自发地从低温物体传递到高温物体B. 所有自然过程都会导致熵增加C. 熵是状态函数D. 熵是过程函数答案:D6. 在电化学中,哪个术语用于描述电子的流动?A. 电流B. 电压C. 电阻D. 电势答案:A7. 什么是电解质?A. 一种不导电的物质B. 一种在溶液中不产生离子的物质C. 一种在溶液中产生离子的物质D. 一种在熔融状态下产生离子的物质答案:C8. 根据阿伏伽德罗定律,1摩尔任何气体在标准状态下的体积是多少?A. 22.4 LB. 22.4 mLC. 224 LD. 224 mL答案:A9. 什么是布朗运动?A. 原子的无规则运动B. 分子的无规则运动C. 电子的无规则运动D. 离子的无规则运动答案:B10. 在理想气体的范德瓦尔斯方程中,b代表什么?A. 气体分子的体积B. 气体分子间的相互作用力C. 气体分子的动能D. 气体分子的势能答案:A二、填空题(每题2分,共20分)1. 摩尔质量的单位是______。
答案:克/摩尔2. 理想气体状态方程的公式是______。
答案:PV=nRT3. 热力学第一定律表明能量______。
答案:守恒4. 温度的单位是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章例4 在100℃,p下,1mol 水(1)可逆蒸发, (2)向真空蒸发为蒸气。
已知 vap H m=kJ mol-1, 假设蒸气为理想气体,液体水的体积可忽略不计,求Q, W, U, H 。
解:(1) H = Qp = W = -pV = -p V g =- RT =U = Q-W = =(2) 始终态同(1) 故H = U = 向真空蒸发W = 0 Q =U =例5 将100g,40℃水和100g, 0℃的冰在杜瓦瓶中(恒压,绝热)混合,求平衡后的状态,及此过程的H 。
已知冰的熔化热 =335J g-1 ,Cp (水)= JK-1g-1解:设水和冰为系统。
因恒压,绝热 所以H = Qp = 0又H =H (水) + H (冰) = 0设终态温度为T H =H (水) + H (冰)=100(T – 313)+ 100335=0T = 253K 该结果是不可能的!100g 水全部降温至0℃,放热:H (水)= – 10040 = –100g 冰全部融化吸热:H (冰)=说明冰不能全部融化,终态应是0℃的冰水混合物。
设 m 克冰融化,H =H (冰)+H (水)= m m = 50g平衡后的状态为50g 冰和150g 水的0℃的冰水混合物。
例6 已知某气体的状态方程为: p T p T V U VT -⎪⎭⎫⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂p TT V T V p H ⎪⎭⎫⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂pV m = RT + bp (b >0常数) 请依据推导结果判断(1)在绝热自由膨胀过程中,该气体的温度如何变化 (2)在绝热节流膨胀过程中,该气体的温度如何变化 解:(1) 绝热自由膨胀过程是等内能过程,U =0,则 所以本题要解的是μJ 的正负令U =f (T, V ),根据循环关系式:现在只要判断[ ]是>0, =0, 还是<0其中的偏微商 与气体的状态方程有关。
焦耳系数 气体的状态方程可改写为 p (V m –b )= RT 其中 对T 求导得:代入上式:故温度不变 分析:若把气体的状态方程p (V m –b )= RT 与理想气体的状态方程pV m = RT 比较, 有什么结论可看出该方程只修正了气体分子的体积(V m –b ),而分子间作用力这一项没有修正,说明p=p 理气, 故在绝热自由膨胀过程中温度没有变化。
若是范德华气体,在绝热自由膨胀过程中温度将如何变化范德华气体气态方程 ()dV T V VU V T ⎰∂∂=∆211-=⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂T U V U V V T T U TJ V U V C ⎪⎭⎫⎝⎛∂∂=μT V UJ V U C V T ⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫⎝⎛∂∂=1μ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂-=V V T p T p C 1VT p ⎪⎭⎫⎝⎛∂∂⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂=V V U J T p T p C V T 1μb V RT p m -=bV R T p m V -=⎪⎭⎫ ⎝⎛∂∂01=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--=⎪⎭⎫⎝⎛∂∂b V R T p C V T m V U ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫⎝⎛∂∂=V V U J T p T p C V T 1μ()RT b V V a p m m =-⎪⎪⎭⎫ ⎝⎛+2即 对T 求导所以在绝热自由膨胀过程中,范德华气体的温度下降。
(2) 绝热节流膨胀过程 H =0,则 所以本题要解的是J-T 是>0,=0, 还是<0。
令H =f (T,p )现在只要判断[ ]是>0, =0, 还是<0其中的偏微商 与气体的状态方程有关。
根据气态方程得 对T 求导得代入上式:在绝热节流膨胀过程中,该气体的温度上升。
例7 装置如图,始态时绝热理想活塞两侧容器各为20dm3,均充满25℃, p的N2。
对左侧气室缓慢加热,直至室内压力为2p 。
请分别以右室气体,左室气体和全部气体为系统,求算Q, W,U , H (N2可视为理想气体)加热解: (1)以右室气体为系统因绝热,Q =0;U =W 。
左室缓慢加热,所以活塞右移可视为绝热可逆压缩,终态压力也为2p2m m V a b V RT p --=bV R T p m V -=⎪⎭⎫ ⎝⎛∂∂012<-=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--=⎪⎭⎫⎝⎛∂∂m V m V U V C a b V R T p C V T ?)(21==∆⎰∂∂dp T p p H p T 1-=⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂T H p H p p T T H T p H p H C p T ⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂1⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛∂∂=V T V T C p p 1pT V ⎪⎭⎫⎝⎛∂∂⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂=-V T V T C p T p p H T J 1μb p RT V m +=p R T V p=⎪⎭⎫ ⎝⎛∂∂⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛∂∂=-V p R T C p T p H T J 1μ0<-=pC b双原子分子理想气体 = 7/5=p1V1 =p2V2V2 = dm3或p11-T1 =p21-T2T2 =U = W = (p2V2 p1V1)/( 1 ) =或n = p1V1/RT1 =U= nCV,m(T2 T1)=H = U =(2) 以左室气体为系统W(左)= –W(右)=V2’ = 40 – = dm3T2’ = 828Kn = p1V1/RT1 =U = nCV,m(T2’ –T1)=H = U =Q = U - W =(3) 以全部气体为系统W(总)= 0Q =U(总)= Q =H(总) = U(总)=第二章例5. 苯的沸点为C,设蒸气为理想气体,求1mol苯在C时下列过程的A, G(1) C6H6(l, p y) C6H6(g, p y)(2) C6H6(l, p y) C6H6(g,(3) C6H6(l, p y) C6H6(g,根据所得结果能否判断过程的可能性解:(1)此为可逆相变, (G )T,p = 0(A )T= Wr= –RT = kJ(2) 该过程可看作: C6H6(l, p y)C6H6(g, p y)C6H6(g,可逆相变 + 理想气体的定温变压过程 故G=G1+ G2 = 0+RT ln(p2 /p1)= 348 J A=A1+ A2 =103 348=kJW =(g)=-RT = kJ (A)T< W , 不可逆过程(3) 同理 G=G1+ G2= 0+RT ln(p2 /p1)= 241 J A=A1+ A2 =103 +241=2 .70 kJ(A)T > W , 不可能例6 在5℃时,过冷液态苯的蒸气压为2632 Pa ,而固态苯的蒸气压为2280Pa 。
已知1mol 过冷液态苯在 5℃凝固时S m = J K-1 mol-1, 设气体为理想气体,求该凝固过程的G 及H 。
解:设计等温变压可逆过程G1 + G5 =Vl ( pl – p y )+ Vs ( p y – ps ) 0( 5℃, p )G = G1 + G2 + G3 + G4 + G5J p p RT Vdp G slp p lsgid 320ln.3-==∆⎰== G3= 320 JH= G +T S = 320 + 268( )=J例7 在一个带活塞的容器中(设理想活塞)有氮气,容器底部有一密闭小瓶,瓶中有水。
整个系统恒温恒压 (373K, p y)。
今使小瓶破碎, 在维持压力为 p y 下水蒸发为水蒸气。
已知vap H my (373K)= kJmol-1 。
氮气和水蒸气可视为理想气体。
求此过程的Q, W,U, H, S, A, G先求可逆相变的Q, W, U,H, S, A, G,其中vap G =0, 再求混合过程的S, A, G , 其中mix U =0, mix H =0当H2O(l )H2O(g)时,体积增大,做体积功:Qp = vapH = n vapHm y= = kJW =- p yV =-nRT = kJvapU =Q + W = kJ vapS =H /T = J K-1(vapA)T = Wr = – nRT = – kJ vapG = 0然后定温定压下水蒸气与氮气混合,但理想气体混合时无热效应,即 mixU=mixH =0。
mixA = mixG = – T mixS = – kJ⎪⎪⎭⎫⎝⎛+++=∆B B A B A B A Amix V V V n V V V n R S ln ln ii mix V V R n O H S N S S ln)()(22∑=∆+∆=∆()13435.9ln 5.14ln 5.0314.8-⋅=+=K J )()()()(2222O H N O H N mix Vdp Vdp G G G ⎰+⎰=∆+∆=∆)()(22O H N mix pdV pdV A ⎰-⎰-=∆=故U = vapU = kJH = vapH =S = vapS + mixS = J K-1 A =vapA+ mixA = – kJG = 0+ mixG = – kJ 或在已算出U , H , S (总)的基础上A = U – T S = – kJ G =H – T S = – kJ或:在已算出U,H (总)的基础上G (总) = mix G = G (N2)+ G (H2O)= ∫Vdp (N2)+ ∫Vdp (H2O)再计算S (总)= (H –G ) / T = J K-1A (总) = U – T S = – kJ例8. 1mol 某气体从Vm,1 经绝热自由膨胀过程到Vm,2 , 求S 。
已知:气态方程为:p (Vm-b )=RT解:绝热自由膨胀: U =0绝热不可逆过程: S >0。
例9. 某实际气体状态方程为pVm (1 – bp ) = RT , 经节流膨胀后, 压力从p1 p2, S =解:dH = TdS + Vdp = 0 (节流膨胀)⎪⎪⎭⎫ ⎝⎛+=∆**ln ln B A p p n p p n RT G B B A A mix ()B B A A x n x n RT ln ln +=()kJ48.3ln5.1ln 5.0373314.84341-=+⨯⨯=0=-=pdV TdS dU mV V mm V V dV b V RdV T p S m m m m ⎰⎰-==∆2,1,2,1,bV bV R S m m --=∆1,2,ln ⎰⎰--=-=∆2121)1(p p p p dp bp p Rdp T V S例10. 若定容摩尔热容CV,m 与温度无关,试证 (1)1mol 范德华气体从T1,Vm,1 T2, Vm,2(2)范德华气体绝热可逆过程方程式为常数 (3)1mol 范德华气体经绝热自由膨胀过程,从 V1V2,求终态的温度T 2 提示:先求出焦耳系数的表达式 证:(1)任何单相纯物质的熵变公式为:根据该气体的状态方程求出范德华气态方程:(2)范德华气体绝热可逆过程: S =0,即即常数(3) 绝热自由膨胀过程: U =0⎰⎪⎪⎭⎫⎝⎛-+-=2111p p dp bp b p R bV b V R T T C S m m m V --+=∆1,2,12,ln ln=-mV C R m b V T ,/)(dV T p T dT C dS V V ⎪⎭⎫⎝⎛∂∂+=dV T p T dT C S VV V T T m V m m m ⎪⎭⎫ ⎝⎛∂∂+=∆⎰⎰2,1,21,VT p ⎪⎭⎫ ⎝⎛∂∂RT b V V a p m m =-⎪⎪⎭⎫ ⎝⎛+)(22mm V ab V RT p --=bV R T p m V -=⎪⎭⎫⎝⎛∂∂⎰⎰-+=∆2,1,21,m m V V mT T m V m b V dV R T dTC S bV b V R T TC m m m V --+=1,2,12,ln ln 0ln ln1,2,12,=--+=∆bV b V R T T C S m m m V m Rm m C b V b V T T mV ⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛2,1,12ln ln ,=-mV C R m b V T ,/)(dV V T T UV V ⎪⎭⎫⎝⎛∂∂=∆⎰211-=⎪⎭⎫⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂TU V U V V T T U令 U =f (T , V )从范德华气态方程 可知:积分:例3 60℃时,p A*= , p B*= ,在该温度时A 和B 可形成稳定化合物AB , p AB*= 。
