力矩和力偶
力矩与力偶

1.2.2 力矩的性质 1.力F对O点这矩不仅取决于F的大小,同时还与矩心的位置即力臂d有关。 2.力在刚体上沿作用线移动时,力对点之矩不变。 3.力的大小等于零或力的作用线过矩心时,力矩等于零。 4.互成平衡的两个力对同一点之矩的代数和为零。
§1.2 力对点之矩
1.2.3 合力矩定理 平面力系有一合力时,合力对平面内任一点之矩,等于各分力对同一点之 矩的代数和。
Ft
D 2
0
Fn
cos
D 2
1000 160 103 cos 20 75.2N m 2
计算力对点之矩的方法:1.利用力对点之矩的定义式计算。 2.利用合力矩定理计算。
§1.3 力偶
生活实例:
1.3.1 力偶的概念 1.力偶的定义:一对大小相等、指向相反的平行力组成的特殊力系称为力
偶。记作F , F 。
§1.3 力偶
性质1 力偶在任一轴上的投影的代数和为零。 力偶无合力,力偶对刚体的移动不产生任何影 响,即力偶不能与一个力等效,也不能简化为 一个力。
性质2 力偶对于其作用面内任意一点之矩与该 点(矩心)的位置无关,它恒等于力偶矩。
1.3.2 力偶的基本性质
§1.3 力偶
推论1 力偶可在其作用面内 任意移而不会改变它对刚体 的转动效应。
思考题:如图所示的圆盘,在力偶M=Fr和力F的作用
下保持静止,能否说力偶和力保持平衡?为什么?
§1-4 力的平移定理
力的平移定理 力可以等效的平移到刚体上的任一点,
但必须附加一个力偶,其力偶矩的大小等 于原力对该点之矩。
§1.4 力的平移定理
力的平移定理换句话说,就是平移前的一个力与平移后的一个力和一个附 加力偶等效。即一个力可以分解成为同平面内另一点的一个力和一个力偶。反 之共面的一个力和一个力偶也可以合成为同平面内的一个力,这便是力的平移 定理的逆定理。
力矩-力偶系
a b
M o (F ) Fd F (ob ab) F (l sin h cos )
2.合力矩定理 • 力系与其合力等效,对于使物体转动的效果,这种 性质依然存在,即合力对于一点O之矩,等于各分 力对点O之矩的代数和,这一普遍规律称为合力矩 定理。可用下式表示。
式中:
§1-3 力对点之矩、力偶
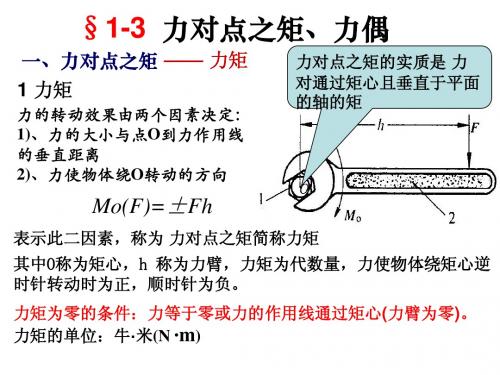
一、力对点之矩 —— 力矩 1 力矩
力的转动效果由两个因素决定: 1)、力的大小与点O到力作用线 的垂直距离 2)、力使物体绕O转动的方向
式中, Mo(F)=±Fh 表示此二因素,称为 力对点之矩简称力矩 力对点之矩的实质是 力 对通过矩心且垂直于平面 的轴的矩
其中O称为矩心,h 称为力臂,力矩为代数量,力使物体绕矩心逆 时针转动时为正,顺时针为负。
例题:梁AB 受一主动力偶作用,其力偶矩M=100 Nm ,梁长l=5m ,梁的自重不计,求两支座的约束 反力。 • 解 (1)以梁为研 究对象,进行受力 分析并画出受力图 • 因系统为力偶系, 故FA必须与FB大 小相等、方向相反、 作用线平行。 • (2)列平衡方程
∑M=0
FBl - M = 0
(1)力偶无合力。 力偶不能用一个力来等效,也不能用一个力来平衡。 可以将力和力偶看成组成力系的两个基本物理量。 (2)力偶对其作用平面内任一点的力矩,恒等于其力偶矩。
2.力偶的性质
(3)力偶的等效性——作用在同一平面的两个力偶,若它 们的力偶矩大小相等、转向相同,则这两个力偶是等效的。 则可得: • 1)力偶可以在其作用面内任意移转而不改变它对物体的作 用。即力偶对物体的作用与它在作用面内的位置无关。 • 2)只要保持力偶矩不变,可以同时改变力偶中力的大小和 力偶臂的长短,而不会改变力偶对物体的作用。
力矩与力偶的异同点

《力矩与力偶的异同点》
小朋友们,今天咱们来聊聊力矩和力偶,看看它们有啥相同的地方,又有啥不一样的地方。
先来说说啥是力矩。
比如说,咱们想打开一扇很重的门,得在门把手上用力推或者拉,这个让门转动的效果,就是力矩在起作用。
那力偶呢?想象一下,有两个人,一个在这边推,一个在那边拉,而且他们的力大小一样,方向相反,这样让物体转动的情况,就是力偶。
那它们有啥相同点呢?它们都能让物体转动起来。
就像咱们玩的小陀螺,有力矩或者力偶作用,它就能转起来。
再说说不同点。
力矩是一个力产生的让物体转动的效果,而力偶是两个大小相等、方向相反的力一起产生的转动效果。
给大家讲个小故事。
有一次,小明想把一个大箱子转个方向。
他自己在一边用力推,这就是力矩。
可是箱子太重了,推不动。
后来他找来了小伙伴,小伙伴在另一边和他用一样大的力,方向相反地拉,这就变成了力偶,然后箱子就转动啦。
还有哦,咱们骑自行车的时候,脚蹬子带动链条,这就产生了力矩。
但是如果两个轮子受到的地面摩擦力不一样,这两个摩擦力就形成了力偶,会影响车子的平衡。
小朋友们,虽然力矩和力偶有点复杂,但是多想想这些例子,就能慢慢明白啦。
以后在生活中,大家也可以多观察,看看哪些地方有力矩,哪些地方有力偶,这样就能更好地理解它们啦。
小朋友们,现在是不是对力矩和力偶的异同点有点清楚啦?。
《力矩和力偶》 讲义

《力矩和力偶》讲义一、引言在力学的世界里,力矩和力偶是两个非常重要的概念。
它们在物理学、工程学以及日常生活中的许多现象和问题中都有着广泛的应用。
理解力矩和力偶的概念、性质以及它们的作用,对于我们分析和解决各种力学问题具有至关重要的意义。
二、力矩的概念力矩,简单来说,就是力使物体绕着某个固定点转动的效果。
我们可以想象一下,当我们用扳手拧螺丝时,施加在扳手上的力会使螺丝产生转动,这个力产生的转动效果就是力矩。
力矩的大小等于力与力臂的乘积。
力臂是指从转动轴到力的作用线的垂直距离。
如果用 M 表示力矩,F 表示力,L 表示力臂,那么力矩的计算公式就是 M = F × L 。
为了更好地理解力矩的方向,我们引入了右手螺旋定则。
右手握住转动轴,四指的弯曲方向沿着力的方向,那么大拇指所指的方向就是力矩的方向。
三、力矩的平衡在一个物体处于平衡状态时,作用在它上面的所有力矩之和必须为零。
这就是力矩平衡的条件。
例如,一个跷跷板,如果两端的重量和距离转动轴的长度满足一定的关系,跷跷板就能保持平衡。
力矩平衡在工程和日常生活中有很多应用。
比如建筑结构中的梁柱,必须保证受到的力矩平衡,才能保证结构的稳定和安全。
四、力偶的概念力偶是由大小相等、方向相反、作用线不在同一直线上的两个平行力组成的。
这两个力的合力为零,但它们能使物体产生转动效果。
例如,用两只手同时在门的两边施加大小相等、方向相反的力,门就会绕着门轴转动,这就是力偶的作用。
力偶矩是用来衡量力偶使物体转动效果的物理量,它等于其中一个力的大小与两个力之间的垂直距离的乘积。
五、力偶的性质力偶具有以下几个重要的性质:1、力偶对其作用平面内任一点的力矩之和恒等于力偶矩,与矩心的位置无关。
2、力偶不能合成为一个合力,也不能用一个力来平衡。
3、力偶可以在其作用平面内任意移动和转动,而不改变它对物体的作用效果。
六、力矩和力偶的区别与联系力矩和力偶既有区别又有联系。
区别在于:力矩是一个力对某一点的转动效果,而力偶是两个力组成的系统产生的转动效果。
力矩和力偶

想一想,说一说
1、车间、仓库的大铁门,在靠近门轴的地方推门,尽管用力方 向垂直于铁门,仍不能将门推开。这是为什么? 2、北方农村的石碾子,往往安装较长的把手,这样推起碾 来 就省力。这又是为什么? 3、试分析下述情况中,物体转动是力矩的作用还是力偶矩的作 用: (1)用扳手拧紧螺母。( 力矩 ) (2)手拧紧液化气钢瓶。 (力偶矩 ) (3)蹬自行车踏板使车前进。 ( 力矩 ) (4)旋转钥匙开锁。 (力偶矩 )
二、力偶
1.什么是力偶 什么是力偶
工程上,把大小相等、方向相反、作用线 相互平行的一对力叫做力偶 力偶。 力偶
2.力偶矩 力偶矩
(1)力偶臂 力偶中的两个力的 作用线之间的距离d 叫做力偶臂 力偶臂。 力偶臂
(2)力偶矩 力偶矩 F的大小与力偶臂d乘积叫做力偶矩 力偶矩。 力偶矩 M=Fd 力偶矩的单位是牛米 牛米,符号是N·m。 牛米
今天作业 习题册:P5,1.4
2.力矩 力矩
(1)力臂 )力臂:从转动轴到力的作用线之间的距离叫做力臂。
力矩。 (2)力矩 )力矩:力F和力臂L的乘积叫做力对转动轴的力矩 力矩 M=FL 力矩的单位是牛米 牛米,符号是N·m。 牛米 (3)力矩可以使物体向不同的方向转动。 )力矩可以使物体向不同的方向转动。
建筑力学-第三章力矩和力偶

平面力偶系平衡的充要条件 M=0
即
Mi 0
人有了知识,就会具备各种分析能力, 明辨是非的能力。 所以我们要勤恳读书,广泛阅读, 古人说“书中自有黄金屋。 ”通过阅读科技书籍,我们能丰富知识, 培养逻辑思维能力; 通过阅读文学作品,我们能提高文学鉴赏水平, 培养文学情趣; 通过阅读报刊,我们能增长见识,扩大自己的知识面。 有许多书籍还能培养我们的道德情操, 给我们巨大的精神力量, 鼓舞我们前进。
2
M Fd
2
2
Mn d
Fn
M F d
n
n
=
=
F F F F
R
1
2
n
F F F F
R
1
2
n
=
=
=
M FRd
F1d F2d Fnd
M M M
1
2
n
n
M M i M i i 1
2.3.2 平面力偶系的平衡方程
第三章 力矩和力偶
第一节 力对点之矩 第二节力偶和力偶矩 第三节平面力偶系的合成与平衡
4.1 力对点之矩
力对物体可以产生 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、方向
一、力对点的矩
MO(F) F d
+—
二、合力矩定理
力系(F1、 F2、 F3、 … Fn)的合力为FR,则 MO(FR)= MO(F1) + MO(F2) +…+ MO(Fn)
4.2.2 力偶矩 力偶中两力所在平面称为力偶作用面。 力偶两力之间的垂直距离称为力偶臂。 三个要素 a.大小:力与力偶臂乘积 b.方向:转动方向 c.作用面:力偶的影响面
力矩和力偶

力矩和力偶
力矩和力偶是力学中的两个基本概念,它们在力的作用方式和使用效果上存在一些区别。
力矩是一个向量,它描述了力对物体产生转动作用的效果,是力对某一轴线或点的作用力矩。
力矩的大小等于力的大小和其到旋转轴或点的距离的乘积,方向垂直于轴或点。
在计算上,力矩等于力与力臂的乘积,其中力臂是从旋转轴或点到力的作用线的垂直距离。
力偶是一对大小相等、方向相反且不共线的平行力,它们的作用效果是使物体产生转动。
这对力在相互垂直的平面上,其中一个力垂直于这个平面,另一个力平行于这个平面。
在实际应用中,力偶可以用来转动锁紧物体,例如螺栓、螺母等。
综上所述,力矩和力偶虽然都涉及到力的作用,但它们的作用方式和使用效果有所不同。
力矩描述的是力对物体产生转动作用的效果,而力偶则是一种产生转动作用的特殊方式。
《力矩和力偶》 讲义

《力矩和力偶》讲义在物理学和工程学中,力矩和力偶是两个非常重要的概念。
它们在理解物体的转动和平衡等方面起着关键作用。
接下来,让我们深入了解一下力矩和力偶。
一、力矩力矩,简单来说,就是使物体转动的能力。
想象一下,你试图用扳手拧松一个螺丝。
当你在扳手的一端施加一个力时,这个力能够使螺丝转动,而衡量这个转动效果的物理量就是力矩。
力矩的大小等于力的大小乘以力臂的长度。
力臂是从转动轴到力的作用线的垂直距离。
如果用 M 表示力矩,F 表示力,L 表示力臂,那么力矩的计算公式就是 M = F × L 。
例如,一个力为 10N,作用点距离转动轴 2m,力臂就是 2m,那么力矩就是 10×2 = 20N·m 。
力矩的方向遵循右手定则。
伸出右手,让四指沿着力绕轴转动的方向弯曲,那么大拇指所指的方向就是力矩的方向。
在实际生活中,力矩有很多应用。
比如开门时,我们在门把手上施加一个力,通过长长的力臂产生较大的力矩,从而轻松地把门打开。
二、力偶力偶是由两个大小相等、方向相反、但不在同一直线上的平行力所组成的系统。
这两个力的合力为零,但它们能够使物体产生转动。
力偶的作用效果仅仅取决于力偶矩的大小和方向,而与力偶中两个力的作用点的位置无关。
力偶矩等于其中一个力的大小乘以两个力之间的垂直距离,即力偶臂。
假设力偶中的两个力大小都为 F ,力偶臂为 d ,那么力偶矩 M 就等于 F × d 。
力偶在工程和日常生活中也很常见。
比如,用两个手指拧动螺丝帽,或者汽车的方向盘在转动时,都是力偶在起作用。
三、力矩与力偶的关系力矩和力偶既有联系又有区别。
联系在于,力偶可以看成是由一对特殊的力矩组成,这对力矩的大小相等、方向相反,且都作用在同一物体上。
区别在于,力矩是单个力对物体转动效果的度量,而力偶是两个力的组合对物体转动效果的度量。
此外,单个力矩可以使物体产生转动和平动,而力偶只能使物体产生纯转动。
四、力矩和力偶的平衡当一个物体处于平衡状态时,作用在它上面的所有力矩和力偶的总和必须为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力偶是力学 的重要概念, 要透彻理解。
平面力偶的力偶矩是代数量。 平面力偶的三要素:力偶矩的大小,力偶的转向,力偶作用面的方位。 3、力偶的性质 (1)力偶不能看成合力,因此力偶不能与一个力平衡,力偶只能与力偶平衡。 (2)力偶对其作用面内任意一点之矩恒等于力偶矩,而与矩心的位置无关。 (3)平面内两力矩,若力偶矩相等,则两力矩等效。 根据以上性质,可得出两个推论: (1)刚体的作用与作用平面的方位有关,而与平面的位置无关。 四、力的平移定理 将一个力分解为一个力和力偶的过程叫做“力向一点平移” 。 平移时需要附加一力偶,附加力偶的力偶矩等于已知力 F 对平移点之矩。 作用在物体上的力平行移动时,将产生一个附加力偶,该力偶的矩等于原力系 对新作用点的矩。这句话有两层意思: (1)这个附加力偶的力偶臂等于原力与 新作用点之间的垂直距离; (2)附加力偶的转向就是原力系的作用点的转向。
§1-3 力矩和力偶 一、力对点之矩 1、概念:力对物体的转动效应用力矩来度量。 2、定义--力对点之矩(力矩) 力对点之矩即为力使刚体绕固定点转动效果的度量。
本节内容力 对点之矩概 念及力矩的 计算、 合力矩 定理; 力偶的 概念及力偶 矩的计算; 力 矩和力偶的 性质; 力的平 移定理
mo ( F ) = ± F d
3、力矩性质 二、合力矩定理 平面力系的合力对平面上任一点之矩等于诸分力对同一点之矩的代数和。
m0 ( F ) = m0 ( F1 ) + m0 ( F2 ) + L + m0 ( Fn ) = ∑ m0 ( Fi )
三、力偶及基本性质 1、力偶的概念:大小相等,方向相反,作用线平行而不重合的两个力所组成 的特殊力系称为力偶。记作(F,F'。力偶对刚体只产生转动效果而不产生移 F F ) 动效果。 2、力偶矩:力偶对刚体的转动效果,用“力偶矩”来度量,它等于力偶中的 一个力与力偶臂(两力间的距离)的乘积,其正负号与平面力矩相同。 M(F、F )= + F d = m F F 3、力偶的性质 根据以上性质,可得出两个推论: 四、力的平移定理 将一个力分解为一个力和力偶的过程叫做“力向一点平移” 。 记为
年 月 日 节 年 月 日 节 年 月 日 节
内 与 要
容 求
力矩和力偶 熟练地计算力对点的矩,理解合力矩定理的意义,并能在计算中应用; 力矩的 基本性质,弄清力矩和力偶矩的区别。 力矩、力偶矩的计算 2—6 (a)(b)(c)(d) 2-10 教 学 内 容 与 方 法 步 骤 附 记
教 学 目 的 重 点 与难点 布 置 作 业
1
和 F 2。
0 0
它们大小分别为:F1 = F cos30 F F2=F sin30 F
0
由合力矩定理,得:
0
mB (F)= mB (F1)+ mB (F2)=F2×b-F1×a F F F F F
=F(b sin30 -a cos30 F
0
)
0
=500(0.2×sin30 -0.1× cos30 )=6.67N.m 三、力偶及其性质 1、力偶的概念 定义:大小相等,方向相反,作用线平行而不重合的两个力所组成的特殊 力系称为力偶。记作(F,F'。 F F ) 力偶对刚体只产生转动效果而不产生移动效果。 2、力偶矩 力偶对刚体的转动效果,用“力偶矩”来度量,它等于力偶中的一个力与 力偶臂(两力间的距离)的乘积,其正负号与平面力矩相同。 记为 M(F、F )= + F d = m F F
/
教 学 内 容 §2-3 力矩和力偶 一、力对点之矩 1、概念 力对刚体易产生移动效应,也可以产生转动效应。 作用在自由体上的将对物体产生绕质心的转动效应, 作用在有固定点的物体 (例如:套在螺母上的扳手或杆钳)上的力将对物体产生绕支点的转动效应。 力对物体绕某点转动的效果,主要由两个因素决定: (1)力的大小与力臂的乘积。 (2)力使物体绕 O 点的转动方向。 2、定义--力对点之矩(力矩) 力对点之矩即为力使刚体绕固定点转动效果的度量。 点 O 即为力矩中心、简称矩心
m0 ( F ) = m0 ( F1 ) + m0 ( F2 ) + L + m0 ( Fn ) = ∑ m0 ( Fi )
在计算力矩时,若力臂不易求出,常将力分解为两个易定力臂的分力(通常 是正交分解)然后应用合力矩定理计算力矩。
例:试求 F 对 B 点之矩。 解:直接计算矩心 B 到力 F 作用线 的垂直距离 d 比较麻烦。可将 F 分解为 两个力 F
力偶的性质 要搞清楚, 力
(2)只要保持力偶矩不便,可以同时改变力偶中力的大小和力偶臂的长短。 偶 的 等 效 定
理可以从简 单例题予以 说明, 不作证 明。
教学方法 与手段
力对点之矩 和力偶的计 算是力学计 算的基本功, 要达到正确 熟练的程度
mo ( F ) = ± F d
d---- 力臂 乘积 Fd---- 力矩的大小 正负号规定:力矩转向逆为正
注意:①平面力对点之矩是一个代数量。单位:N·m , kN·m。 ②力矩中心不一定取在固定点上,而可以取外体上的任一点。 如果是自由刚体,则力对其上任意一点均可取矩(形成抽象化概念) 。 3、力矩性质 (1)力 F 对于 O 点之矩不仅取决于 F 的大小,同时还与矩心的位置有关(力 矩与矩心的位置关系) 。 (2)力 F 对于任一点之矩,不因该力的作用点沿其作用线移动而改变(因 力及力臂大小均未改变) 。即:力沿作用线移动,力矩不变。 (3)力的大小等于零或力的作用及线通过矩心时,力矩等于零。 (4)互成平衡的两个力对于同一点之矩的代数和等于零。即:两个平衡力 对任一点的力矩和为零。 二、合力矩定理 平面力系的合力对平面上任一点之矩等于诸分力对同一点之矩的代数和。
黄 河 水 利 职业技术学院
授 课 日 期 授 课 班 级 课题与主要
.. .. .. .. .. .. .. .. .. .. .. . 装 . .. .. .. .. .. .. 订 . .. .. .. .. . 线 .. .. .. .. .. .. .. .. .. .. ..
课时授课计划
