大学物理——对称性原理
对称性原理在静电场分析中的应用

对称性原理在静电场分析中的应用作者:余杰冉婷来源:《读与写·教育教学版》2018年第05期摘要:在静电场的学习中,求解电场强度和电势的分布是一个难点,也是高中物理竞赛的考查热点。
本文基于对称分析的思想,分析了某些特殊电荷分布的带电体在空间激发的电场、电势的分布问题,并总结了应用对称性原理处理物理问题的一般思路和方法。
关键词:静电场电势对称性中图分类号:G632 文献标识码:A 文章编号:1672-1578(2018)05-0040-021 引言中学生对求解静电场中电场强度、电势分布时,会非常困惑。
因为求解静电场、电势分布大都需要基于电场或电势的叠加原理,通过分析出带电体上的电荷元在周围空间产生的静电场、电势,并通过叠加法或积分求解空间静电场、电势分布。
然而中学生数学基础较弱,对积分知识更是知之甚少。
所以,在大学物理中看似简单、自然的求解方法,不适用于高中物理教学[1]。
对称性是事物具有的一种客观不变性。
对称性也是物理现象和过程在一定变换条件下所保持的某种不变性。
因此对称法解题的特点非常明显,就是采用对物理问题中出现的各种对称性,如物理过程的对称性、运动轨迹的对称性、镜像的对称性、几何形状的对称性等等。
在电场中,当电荷的分布具有对称性时,应用对称性解题非常方便[2]。
本文列举了两种不对称分布的电荷,通过构造某种对称性,求解特殊电荷分布的带电体在空间激发的电场、电势的分布,总结基于对称性原理处理物理问题的一般思路和方法。
2 构造对称分布的静电场运用初等数学方法求解某类特殊电荷分布的静电场分布时,首先应想办法构造某种对称性。
如图1(a)所示,电容器的两块极板呈正三角形,板间距离远小于板的尺寸,电容器内远离边缘处电场强度为E。
由于电荷分布的边缘效应,使得电容器极板角边缘A、B点附近的电场强度显然不再为E。
那么如何分析AB连线中点的场强?[3]显然,图1(a)所示的电容器上电荷分布不具备对称性,而且由于电荷分布的边缘效应,很难直接计算出边缘处的电场分布。
大学物理 第三章 守恒定律与对称性剖析

转动对称P4:
转动90º的整数 倍形状不变。
缔合转换引起 的对称:滑移 反射对称,平 移加镜像反射 后形状不变。
图选自李政道《物理 的挑战》中国经济出 版社, 2002年
缔合转换引起 的对称:将镜 像的黑白两种 颜色互换图形 不变。
图选自杨振宁《基本粒 子发现简史》上海科学 技术出版社, 1963年。原 图为荷兰画家M.C.Escher 所画。
体所做的功。
dA F dr cos Ft dr F dr Biblioteka drFtB F
L
质点沿曲线 L 从A到B力所做的功:
Fn
B
B A
A dA F dr
A
A
L
L
质点沿曲线 L 从A到B力所做的功为力F 沿路径 L 从A到B
的线积分。显然,功是标量其大小与路径有关。
3.合力做的功
若 F F1 F2 Fn
图选自李政道《物理 的挑战》中国经济出 版社, 2002年
对称性在微观世界非常重要:铂针尖上原子对称排 列在场离子显微镜下显示的花样
图选自李政道《物理的挑战》中国经济出版社, 2002年
自然界中非生命的宏观的结构大多是非对称性?
对称性——是时空性质的反映。时间和空间具有各向 同性和均匀性,所以有能量、动量和角动量的守恒。
§2 功和功率
问题提出:考察作用力在空间累积作用的结果使运动 产生怎样的变化? 力在空间上作用的结果:物体在力的作用下产生位移。 功:描述力在空间上积分的物理量。
1.恒力对直线运动物体所作的功
F
S
定义:力对物体所做的功为:
A FS cos F S
2.变力对曲线运动物体所作的功——元功
浅谈分子对称性

浅谈分子对称性摘要:在分子中,原子固定在其平衡位置上,其空间排列是个对称的图像,利用对称性原理探讨分子的结构和性质,是人们认识分子的重要途径,是了解分子结构和性质的重要方法。
分子对称性是联系分子结构和分子性质的重要桥梁之一。
它能简明地表达分子的构型,指导化学合成工作,帮助正确地了解分子的性质,可简化分子构型的测定二作。
关键词:分子对称性对称元素对称操作对称点群群论对称性描述分子的对称性表现并根据分子的对称性对分子作分类。
分子对称性在化学中是一项基础概念,因为它可以预测或解释许多分子的化学性质,例如分子振动、分子的偶极矩和它的光谱学数据(以拉波特规则之类的选择定则为基础)。
在大学程度的物理化学、量子化学与无机化学教科书中,都有关于对称性的章节。
分子对称性的研究是取自于数学上的群论。
一、对称元素分子对称性可分成5种对称元素。
旋转轴:分子绕轴旋转度角后与原分子重合,此轴也称为n重旋转轴,简写为Cn。
例如水分子是C2而氨是C3。
一个分子可以拥有多个旋转轴;有最大n 值的称为主轴,为直角坐标系的z轴,较小的则称为副轴。
n≥3的轴称高次轴。
对称面:一个平面反映分子后和原分子一样时,此平面称为对称面。
对称面也称为镜面,记为σ。
水分子有两个对称面:一个是分子本身的平面,另一个是垂直于分子中心的平面。
包含主轴,与分子平面垂直的对称面称为垂直镜面,记为σv;而垂直于主轴的对称面则称为水平镜面,记为σh。
等分两个相邻副轴夹角的镜面称等分镜面,记作σd。
一个对称面可以笛卡尔坐标系识别,例如(xz)或(yz)。
对称中心:从分子中任一原子到分子中心连直线,若延长至中心另一侧相等距离处有一个相同原子,且对所有原子都成立,则该中心称为对称中心,用i表示。
对称中心可以有原子,也可以是假想的空间位置。
二、对称操作这5种对称元素都有其对称操作。
对称操作为了与对称元素作区别,通常但不绝对的,会加上脱字符号(caret)。
所以?n是一个分子绕轴旋转,而Ê;为其恒等元素操作。
《大学物理》(8-13章)练习题

《大学物理》(8-13章)练习题(2022年12月)第八章气体运动论1.气体温度的微观或统计意义是什么?2.理想气体状态方程的三种形式?PV=N KT, p=nkT, (n=N/V)3.气体的最概然速率、方均根速率、平均速率的关系是什么?4.气体分子的平均平动动能的表达式及其意义?5.理想气体的内能?6.气体分子的平均自由程是指?7.单原子分子、刚性双原子分子气体的自由度数目各是多少?8、理想气体的微观模型是什么?综合练习1. 在某容积固定的密闭容器中,盛有A、B、C三种理想气体,处于平衡状态。
A种气体的分子数密度为n1,它产生的压强为p1,B种气体的分子数密度为2n1,C种气体的分子数密度为3n1,则混合气体的压强p为( )A. 4p1. ;B. 5p1;C. 6p1;D. 8p1.2. 若理想气体的体积为V,压强为p,温度为T,一个分子的质量为m,k为玻尔兹曼常量,R为普适气体常量,则该理想气体的分子数为( )A. pVm⁄; B.pV mT⁄; C. pV kT⁄; D. pV RT⁄.3. 压强为p、体积为V的氢气(视为刚性分子理想气体)的内能为( )A. 52pV; B. 32pV; C. pV; D. 12pV。
4 刚性双原子分子气体的自由度数目为()。
A. 2B. 3C. 4D. 55.气体温度的微观物理意义是:温度是分子平均平动动能的量度;温度是表征大量分子热运动激烈程度的宏观物理量,是大量分子热运动的集体表现;在同一温度下各种气体分子平均平动动能均相等。
6. 设v̅代表气体分子运动的平均速率,v p代表气体分子运动的最概然速率,(v2̅̅̅)12代表气体分子运动的方均根速率。
处于平衡状态下理想气体,三种速率关系为( )A. (v2̅̅̅)12=v̅=v p;B. v̅=v p<(v2̅̅̅)12;C. v p<v̅<(v2̅̅̅)12;D. v p>v̅>(v2̅̅̅)12。
时空对称性

d2r d2r F = m 2 →F = m 2 dt d(t)
牛顿定律具有时间反演对称性 牛顿定律具有时间反演对称性
对 但生活中的许多现象不具有时间反演不变性 称 热力学箭头 君不见黄河之水天上来, 君不见黄河之水天上来, 性 的 时间箭头 心理学箭头 奔流到海不复回. 奔流到海不复回. 基 君不见高堂明镜悲白发, 君不见高堂明镜悲白发, 宇宙学箭头 朝如青丝暮成雪. 本 朝如青丝暮成雪. 概 将无阻尼的单摆(保守系统)拍成影片, 念 将影片倒着放,其运动不会有任何改变—— 保守系统具有时间反演对称性. 保守系统具有时间反演对称性. 武打片动作的真实性: 武打片动作的真实性:
曼德耳布罗特的支气管树模型
2. 置换对称性(联合变换) 置换对称性(联合变换)
对 的骑士图案是镜象反射, ▲ ESCHER的骑士图案是镜象反射,黑白置 称 平移操作构成对称操作. 性 换,平移操作构成对称操作. 的 基 本 概 念
因 三, 因果关系与对称性原理 果 自然 关 对称性与自然规律之间是什么关系? ——自然 规律反映了事物之间的因果关系,其对称性即: 系 规律反映了事物之间的因果关系,其对称性即: 等价的原因 → 等价的结果 与 对 对称的原因 → 对称的结果 称 对称性原理(皮埃尔 居里): 皮埃尔居里 居里) 原 原因中的对称性必反映在结果中, 原因中的对称性必反映在结果中,即结果中的对 理 称性至少有原因中的对称性那样多; 称性至少有原因中的对称性那样多;
对 称 性 与 对 称 破 缺
对称性与对称破缺
对称性概念源于生活 对称性的基本概念 因果性与对称性原理 对称性与守恒定律 对称性的自发破缺 对称性思想方法的重要意义
关于对称性原理的注记
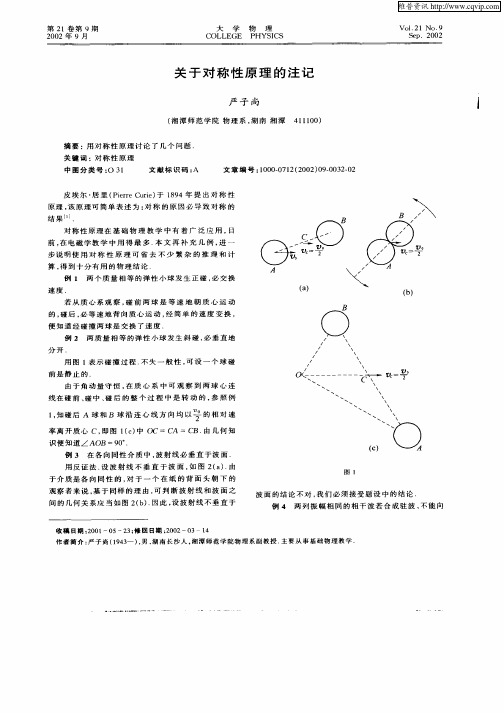
平 均 能 流 密 度 相 同 . 用 反 证 法 , 形 成 驻 波 后 , 于 仍 设 对
任 一 垂 直 于 波 线 的 截 面 , 在 向 左 的 平 均 能 流 , 对 称 存 据 性 原 理 , 存 在 向 右 的 平 均 能 流 , 此 通 过 此 截 面 的 平 必 因 1 20 0 2年 9月 大 学 物 理
V o . NO. 1 21 9 Se p. 2 002
C0 LLE GE PH Y SI CS
关 于 对 称 性 原 理 的 注 记
严 子 尚
( 潭 师范 学 院 物 理系 , 南 湘潭 湘 湖 4 10 ) 1 1 0
观 察 者 来 说 , 于 同 样 的 理 由 , 判 断 波 射 线 和 波 面 之 基 可
图 l
波 面的 结论 不对 , 们 必 须接 受题 设 中 的结论 . 我 例 4 两 列 振 幅 相 同 的 相 干 波 若 合 成 驻 波 , 能 向 不
间 的几何 关 系应 当如 图 2 b . ( ) 因此 , 波 射 线 不 垂 直 于 设
摘 要 : 对称 性 原理讨 论 了几 个 问题 . 用
关 键 词 :对 称 性 原 理 中图分 类 号 : 1 0 3 文献 标 识码 : A 文 章 编 号 :0 00 1 ( 0 2 0 —0 2 0 1 0 — 7 2 2 0 ) 90 3 —2
皮 埃 尔 ・ 里 ( i r C r ) l9 居 Pe e ui 于 8 4年 提 出 对 称 性 r e
Abs r c S m e p o e s a e d s u s d b sn y m e r i i e. t a t: o r blm r ic s e y u i g s m t y prncpl
电场及磁场的对称性分析
电场及磁场的对称性分析第21卷第3期天津职业技术师范大学2011年9月JOURNALOFTIANJINUNIVERSITY0FTECHN0L0GYANDEDUCATIONV oI.21No.3Sep.2011电场及磁场的对称性分析李凤敏(天津职业技术师范大学理学院,天津300222)摘要:利用对称性的概念和矢量场的对称性分析计算方法,讨论了某些具有对称性的带电体场及载流体场的计算,特别是对其中的重点和难点问题进行了详细的分析和论证.对称性方法可以使具有对称性的场的计算问题的物理图像清晰,简化计算,易于理解.关键词:对称性;极矢量;轴矢量;长直螺线管;感生电场;轴对称载流体中图分类号:0441.4文献标识码:A文章编号:2095—0926(2011)03—0047—03 SymmetryanalysisonelectricfieldandmagneticfieldLIFeng——rain(SchoolofScience,TianjinUniversityofTechnologyandEducation,Tianjin300222,China) Abstract:Thefieldsofsomeofthechargedobjectsandcurrentcarryingobjectswithcertainsy mmetriesarecal—culatedusingthesymmetryconceptandsymmetryanalysismethod,andespecially,thekeypo intsindealingwithsuchproblemsareinvestigatedindetail.Indealingwiththeseproblems,symmetryanalysism ethodcanmakethephysicalpicturesmoreclear,thecalculationsmoresimple,andtheunderstandingmucheasier .Keywords:symmetry;polarvector;axialvector;longandstraightsolenoid;inducedelectricf ield;currentcarrierwithaxialsymmetry对称性又称不变性,在自然界普遍存在.对称性是指体系在某种操作下变成与原状态相同或等价的状态.对称性分析在经典物理及理论物理中都有着广泛的应用.在大学物理电磁学教学中常见的对称操作有平移,转动及镜像反射l11等.根据大学物理教学大纲的基本要求,用高斯定理及安培环路定理进行场的计算是学生必须掌握的内容,而这往往又是教学的难点.比如各类教材中都会有这样的例子:长直螺线管磁场变化时产生的感生电场的计算,电动势的计算,轴对称载流体的磁场分布,轴对称带电体的场强分布等.在以往的教材及教学过程中,对此类问题的处理往往都是根据对称性的特点,定性地解释电场及磁场的大小与方向的分布情况.这种处理问题的方法显然缺乏说服力,因此如果能用比较简单的数学方法来证明,这样不仅使教学内容逻辑性更强,同时也会使学生对所学内容理解更深,概念更清楚.1关于场矢量在电磁学部分,我们遇到的场矢量无非是电场及磁场.但由于电场强度E与磁感应强度在镜像反射下具有不同的变换性质,这导致了电场与磁场许多不同的性质.如图1所示,电场强度E是极矢量,即在镜像反射变换下,与镜面垂直的分量反向,平行分量不变;而磁感应强度为轴矢量,即在镜像反射变换下,『E图1电场强度及磁感应强度镜像反射变化收稿日期:2011-05—17作者简介:李凤敏(1965一),女,副教授,硕士,研究方向为物理教学法?48?天津职业技术师范大学第21卷与镜面垂直的分量不变,平行分量反向嘲.正是由于电场强度E和磁感应强度的这一特性,使得在分析具有某种对称性的带电体场或载流体场时会带来很大的方便.2利用对称性分析具体实例2.1长直螺线管磁场变化引起的感生电场在电磁学教学内容中,通常涉及长直螺线管磁场变化时产生的感生电场的计算,比如大部分教材中都有这样一个例题:通有时变电流的无限长直螺线管内的磁场曰随时间变化,如图2所示.已知的数值,cl求它在管内,外激发的感生电场的分布.,/一,一~,\,/,\,//××x,\『,0\××××××'××:,,×××/,/,\,/,/\~一一一,,一般大学物理教材中给出的解通常如下吲:由磁场分布的轴对称性可知,感生电场的分布也具有轴对称性.即以长直螺线管轴线上任意点为中心的同一闭合回路上各处感生电场的大小相等,方向沿回路的切线方向.因此沿该回路的感生电场的环量由下式求得:.d,:一8.ds(1)Jd当r<R时,由(1)式可得:E2叮『r:一1Tr2Q/7故E:一/-二Ub当>R时,由(1)式可得:E2:一:Q故E:一二,Lib对这样的分析过程并不存在异议,但问题是学生并不清楚为什么在这种情况下产生的感生电场呈上述分布,而其他方向上却不存在.对这一问题的处理, 可以从磁场的对称性分布人手得到解答.设长直螺线管内的磁场变化时产生的感生电场为E,以螺线管轴线上任意点为坐标原点,建立柱坐标系,则空间任意点的感生电场为:E=最+E+E(Z轴与I司向)如图3所示,由于长直螺线管内的磁场具有轴对称性且沿z轴的平移不变性,以该轴为轴线做一闭合圆柱面,由磁场分布的对称性可知,在闭合圆柱面s, 5两个圆面上,对应位置的感生电场的大小,方向均相同,对该闭合面,感生电场的通量为零:即:《Eds=0fEl"(Is=JEi"d$+』El"ds+JEi'ds=0Sls2S▲Z图3以螺线管轴线为轴取闭合面(2)由于只有E及,分量对该闭合面的通量有贡献,因此上式积分结果为:Ezs—EzS+E~2'rrrL:0其中,AS为5,5圆面面积.故E=0即感生电场的径向分量为零.如图4所示,做一闭合回路,则感生电场沿该回路的环量由式(3)给出:fEds:一『『粤.ds(3)L?L丑.,,_—.\,i\一一/图4取一闭合回路由于感生电场在螺线管内,外垂直于轴的方向上的数值并不相等,因此由(3)计算可得:(E岛)z=0,由于E≠,且l#0所以岛=0(其中,分男4为螺线管内外的感生电场)第3期李凤敏:电场及磁场的对称性分析?49?即感生电场沿轴向的分量亦为零,由此证明由长直螺线管磁场变化引起的感生电场的分布只存在E分量,亦即空间各处的感生电场只有切向分量.2.2轴对称载流体的磁场对无限长载流圆柱面(或体),其磁场的分布可由安培环路定理给出[41.一般的求解过程中,只是认为此类载流体由于电流分布的对称性可判断出磁场分布的特点,并未给出严格的证明,此处利用对称性原理给出磁场方向的分析.设电流分布关于平面∑镜像对称,则该电流在∑上激发的的磁场必垂直于∑平面[51(当≠0时),如图5所示图5关于平面对称的电流元在载流圆柱面上任意对称的位置,A:取两个关于平面对称的电流元,ldZ,hall:,分别记为a与b,两电流元到∑平面上任意P点的位矢分别为,和r2,D点为两电流元连线与∑平面的交点,建立图4所示坐标系,由对称性可知:ax=bx,=by,=一bz;/'2x=rh,r=n=0,r五=一rk(4)根据毕奥一萨伐尔定律,任意电流元的磁场为::掣,为此分别计算口Xrl及bXr2onr根据矢量叉乘公式:A×B=(Aysz—A)f+(一A』+(一A)可得:axg1=(k一~zt'ly)f+(rl一kj,+(y—l);b×,=(6,一b.rzy)i+(6,—bxr~)j+(6一byrz~)k;所以(a×,.1+b×r2)=(actk一r1+6,一6.r2v)f+(r1一rk+6一b~r2,)j+(Ctxrl一ayr1+b~rzy—byrz~)k. 利用式(4)的对应关系,可以得到下述结果:(a×,1+b×g2)=(~xl'ly—r上,1+bxr升一byrz~)k= (一ayrk—bT~)k≠0.由此可知,任何关于平面∑呈对称分布的电流元产生的磁场均垂直于对称面.根据上述分析可以断定载流圆柱面(或体)的磁场分布的规律.通过比较直观的数学证明,可以帮助学生深入理解呈轴对称载流体的磁场分布特点.2.3无限长均匀带电圆柱面的电场对无限长均匀带电圆柱面来说,教材中的解均为根据电荷分布的轴对称性认为电场的分布同样也是轴对称的,然后取一同轴的闭合圆柱面直接利用高斯定理解出[31.当然此类问题也可直接积分得出结果,但积分求解过程较麻烦且对大多数学生来说此积分运算困难.在此可以直接利用对称性证明无限长均匀带电圆柱面的场强的方向分布特点.由于此带电体电荷分布为轴对称的,在此不妨设空间的电场分布为:E=Ez+Er+E其中,最,E,为柱坐标系中的3个分量(取对称轴为z轴).过对称轴做一平面,显然带电体关于这一平面是镜像对称的.电场关于此平面同样镜像对称.由于E是极矢量,在镜像反射下应有:=一,另一方面镜像对称要求=,因此只有=0满足条件.同样做一垂直于对称轴的任一平面,显然该平面亦为此带电体的镜像对称面,因此由电场强度是极矢量,可以用同样的方法证明E=0.至此证明了场强的分布只有径向分量E存在.3结束语通过以上几个具体实例,可以看到利用对称性可以很直观地证明电荷及电流分布具有对称性场方向的分布特点.电磁学中关于具有对称分布的带电体及载流体类型较多,因此在解题之前不妨先考虑用对称性分析的方法对场的分布情况进行简要的证明,这样既有利于简化计算,同时又可以帮助学生加深对场概念的理解.参考文献:[1]孙海滨.物理学中的对称性与守恒律[J1.物理与工程, 2006,16(4):49—52.[2]陈熙谋,赵凯华.电磁学教学中对称性分析的积极意义[J].大学物理,2005,24(4):3—5.[3]程守洙,江之永.普通物理学[M].5版.北京:高等教育出版社,1999.[4]张三慧.大学物理学——电磁学[M].2版.北京:清华大学出版社,1999.[5]梁灿斌,秦光戎,梁竹健.电磁学[M].2版,北京:高等教育出版社,2008.。
大学物理学(下册)(第二版)(李承祖主编)PPT模板
3
费衍射光栅光谱和光
栅分辨本领
第四部分振动波动电磁波和波动光学
第21章波动光学(ⅲ)
21.1光的偏振 态偏振光的获 得
21.4偏振光的 干涉
21.2双折射现 象
*21.5人工双 折射
21.3偏振棱镜 波片圆和椭圆 偏振光的产生 和检验
问题和习题
04
o
n
e
第五部分相对论物理学中的对称性
第五部分相 对论物理学 中的对称性
01
o
n
e
前言
前言
02
o
n
e
第一版前言
第一版前言
03
o
n
e
第四部分振动波动电磁波和波动光学
第四部分振动波动 电磁波和波动光学
06
第21章波动 光学(ⅲ)
01
第16章振动
05
第20章波动 光学(ⅱ)
02
第17章机械 波
04
第19章波动 光学(ⅰ)
03
第18章电磁 波
第四部分振动波动电磁波和波动光学
01 1 7 .1 机 械波的产生 02 1 7 .2 平 面简谐波
和传播
03 1 7 .3 机 械波的能量 04 1 7 .4 惠 更斯原理波
密度和能流
的衍射、反射和折射
05 1 7 .5 波 的相干叠加 06 1 7 .6 多 普勒效应
驻波
第四部分振动波动电磁波和波动光学
第17章机械波
问题和习题
25.1对称性的概念 和描写方法
01
05
02
25.2时空 对称性和物 理量、物理 规律、物理 相互作用
04
03
*25.4动力学对称性
大学物理电子教案(西南交大)1-1
1次轴 次轴
⋅O
2次轴 次轴
.O .o
3次轴 次轴 . O
4次轴 次轴
O
第8页 共39页 页 页
物理定律的旋转对称性——空间各向同性 空间各向同性 物理定律的旋转对称性
大学物理
空间各方向对物理定律等价,没有哪一个方向具有 空间各方向对物理定律等价, 特别优越的地位。 特别优越的地位。 实验仪器方位旋转,实验结果不变。 实验仪器方位旋转,实验结果不变。 例如:实验仪器取向不同, 例如:实验仪器取向不同, 得出的单摆周期公式相同。 得出的单摆周期公式相同。
第13页 共39页 页 页
大学物理
物理定律的空间反射对称性 如果在镜象世界里的物理现象不违反已知的物理规律, 如果在镜象世界里的物理现象不违反已知的物理规律, 则支配该过程的物理规律具有空间反射对称性。 则支配该过程的物理规律具有空间反射对称性。 (2) 时间对称性 1) 时间平移对称性 一个静止不变或匀速直线运动的体系对任何时间间 的时间平移表现出不变性。 隔 ∆t 的时间平移表现出不变性。而周期性变化体系 单摆、弹簧振子) (单摆、弹簧振子)只对周期 T 及其整数倍的时间平 移变换对称。 移变换对称。
同学们好!
第一章 对称性与对称破缺
大学物理
H. 邦迪 美是探求物理学中重要结果的一个指导 邦迪:“美是探求物理学中重要结果的一个指导 原则” 原则”。 [美]阿.热 在《可怕的对称》一书中说 “审美事实 可怕的对称》一书中说: 审美事实 美 阿热 上已经成了当代物理学的驱动力 驱动力” 上已经成了当代物理学的驱动力”。 从这种“指导原则” 从这种“指导原则”或“驱动力”中可以引出一 驱动力” 个重要概念——对称性。 对称性。 个重要概念 对称性 “物理学在 世纪取得了令人惊讶的成功,它改变 物理学在20世纪取得了令人惊讶的成功 物理学在 世纪取得了令人惊讶的成功, 了我们对空间和时间、存在和认识的看法, 了我们对空间和时间、存在和认识的看法,也改变了 我们描述自然的基本语言。在本世纪行将结束之际, 我们描述自然的基本语言。在本世纪行将结束之际, 我们已拥有一个对宇宙的崭新看法, 我们已拥有一个对宇宙的崭新看法,在这个新的宇宙 观中物质已失去了它原来的中心地位, 观中物质已失去了它原来的中心地位,取而代之的是 —— 斯蒂芬.温伯格 斯蒂芬. 自然界的对称性。 自然界的对称性。”
大学物理对称性与守恒定律
“猛然打开了科学中一个黑暗领域的大门。”
——法拉第
马赫的困惑:
马赫 (奥地利) 1838-1916
N N S S
条件-
导线、磁针均垂直于镜面, 结果- 磁针偏转,与镜面平行。 镜面内右手螺旋法则不成立。
N S
N
S
N
S
解释:磁针磁性是安培分子 电流形成的,条件中存在平 行于镜面的因素。
N S N
S
实验仪器方位旋转,实验结果不变。
例如:实验仪器取向不同, 得出的单摆周期公式相同。
T 2
L g
2.空间平移对称 无限长直线:对沿直线移动任意步长的平移操作对称。 无限大平面:对沿面内任何方向、移动任意步长的平 移操作对称。 平面网格:对沿面内某些特定方向、移动特定步长 的平移操作(不变元)对称。
例如:在地球、月球、 火星、河外星系…进行 实验,得出的引力定律 (万有引力定律、广义 相对论)相同。
3.空间反射对称(镜象对称、左右对称、宇称) 相应的操作是空间反射(镜面反射) 。
动物在镜子面前的表现可以反映其智力高低。 令人意想不到的是,一面 镜子竟然能够在拯救一个 物种中发挥作用: 红鹳因为其镜像而以为自 己处在大群中,获得安全 感而繁殖。
学时:2
对称性的概念最初来源于生活:动物、植物、 建筑、文学艺术……
何其相似!
C60分子结构(巴基球) 截角正20面体,每个 顶点上一个C原子, 构成笼状32面体(20 个六边形,12个五边 形)。1985年发现 ( 1996 诺贝尔化学 奖),开创有机化学 新篇章。
药物设计应用举例:一种新开发的用于磁共振成像 的水溶性造影剂,避免其中金属原子对人体的潜在 危害。
对称性与自然规律之间是什么关系?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A I
I1
R
C
R
I I1
R
I I1
I R D R I1 B
解 :电路对 B 、A节点置换对称,设电流如图示
节点 A的电流:I = I1 +(I I1)
节点 C → D 的电流:
I1 (I I1)= 2 I1 I
ቤተ መጻሕፍቲ ባይዱ17
A I
I1
I I1
(2)
RC
(1)
R
RD
R
I I1
I R I1 B
从AD沿(1)和(2)两条路的电压相等:
RI1 + R(2I1I)=2R(I I1 )
3 I1 5 I
RAB
U AB I
I1R I I1 2R
I
7 R
5
18
四. 对称性与守恒定律 (诺特定律) 每个守恒定律对应于一种对称性。
▲ 空间平移对称性与动量守恒定律 有空间平移对称性的系统,其动量必守恒。
▲ 空间的各向同性与角动量守恒定律 若系统中的物理现象和系统所处方位无关, 则系统具有转动对称性(各向同性)。 有转动对称性的系统,其角动量必守恒。 空间各向同性将导致角动量守恒定律成立。
根据镜象反射的性质可将物理学中的矢量
分成两类: 极矢量 和 轴矢量
6
极矢量:镜象反射中垂直反射面的分量反向,
平行反射面的分量不变向。
如:r,v,a,E ,…
v′ v v′
v
v′ v
v′ v
v′
v
反射面
7
轴矢量(赝矢量):镜象反射中垂直反射面的
分量不变向 ,平行反射面的分量反向。
如:,L,pm,B, …
dr t t
▲v
v
v
-v
dt dt dt
d2
r
t t
▲a dt2
dt2 dt2
a
g
上 抛
g
下 落
10
▲ 力对时间反演变换有两种情况: 保守力只与物体相对位置有关, 故对时间反演不变。 耗散力与速度方向有关, 故对时间反演变化。
▲ 牛顿第二定律对保守系统时间反演不变, 对非保守系统则不具有时间反演不变性。
y′
x
空
镜面反射
z′
·o
z y
间
反=
+
绕镜面法线
x′
点对称性
演
旋转 180°
9
2. 时间操作与时间对称性 ①时间平移:t t t0 的变换。 ▲ 静止物体对时间平移具有对称性;
▲ 匀速运动物体的速度对时间平移具有对称性;
▲ 周期系统对时间平移整数周期具有对称性。
②时间反演:t t 的变换(时间倒流)。
14
三. 对称性原理 自然规律反映事物之间的 “ 因果关系 ” 。 稳定的因果关系要求有可重复性和预见性, 即相同的原因必定产生相同的结果。 对称性原理:(Pierre Curie 1894年) (1)原因中的对称性必然存在于结果中; (2)结果中的不对称性必然存在于原因中。 对称性原理是凌驾于物理规律之上的自然界 的一条基本原理。
3
二. 基本操作与对称性的分类
1. 空间操作与空间对称性
①平移:r r r0 的操作。
y
d
x
·
· · ··
· ·
(a)
d (b)
(c)
平移对称 平移 d 对称 无平移对称
(d) 宏观上平 移对称
对平移操作状态不变的系统具有平移对称性。
4
②转动:绕某个定轴旋转一个角度的操作。
轴·
·
轴
轴·
(a)
—完—
21
▲ 统计规律(如扩散)没有时间反演不变性。 研究系统时间反演的性质要区分宏观和微观。
11
3. 联合操作与对称性 有的系统对某种操作可能不具有对称性, 但对几种操作的联合却可能具有对称性。
例如:
对称操作:
绕中心转180°+黑白置换
12
对称操作:镜象+黑白置换+平移操作
13
伽里略变换、洛仑兹变换是时空联合操作, 牛顿定律对伽里略变换是不变的,但对洛仑 兹变换是改变的。 物理学中除上述的时间、空间操作外, 还 涉及到一些其它的操作,例如:电荷共轭 变换(粒子与反粒子的变换),规范变换, 全同粒子置换等等。 它们也和系统的某些 对称性相联系。
15
对称性应用举例:
▲ 根据对称性原理论证
质点在有心力场的作 力心
· 用下,必在同一平面
内运动。
v0
· f m
▲ 论证质心系中两个质 量相等的球对心碰撞 后,速度必在球心联
C
·· · o1 o2
mm
v10
v20
线上,且大小相等、
v1
v2
方向相反。(动量守恒)
16
▲ 复联电阻的计算
如图,求 RAB =?
对称性简介
1
对称性的规律具有极大的普遍性和可靠性, 它是统治物理规律的规律。 对称性分析在物理学中占有重要地位。
本讲目录
一. 操作与对称性的概念 二. 基本操作与对称性的分类 三. 对称性原理 四. 对称性与守恒定律 参考书目
2
一. 操作与对称性的概念 1. 操作(operation) 把系统从一个状态变到另一个状态叫操作, 操作也称为变换。 2. 对称性(symmetry) 若一个系统对某种操作状态不变(等价), 则该系统对此操作具有对称性(H.Weyl.1951), 这样的操作称对称操作(symmetry operation)。
19
▲ 时间均匀与能量守恒定律 若系统中的物理现象和时间平移无关,则 说明时间是均匀的。 时间的均匀性将导致能量守恒定律的成立。 具有时间平移对称性的系统,其能量必守恒。
Emmy Noether 艾米 诺特
20
参考书目
▲ 新概念物理教程《力学》赵凯华、罗蔚茵 ▲《对称》 H. Weyl 商务印书馆 1986 ▲《大学物理学》(第一册) 张三慧 主编 ▲ “Lecture on Physics” R.Feynman. Vol.1
··
L′ L
L′
L
··
L′
L
反射面
L′ L
r p L
(极) (极) (轴)
可以证明:极矢量×极矢量 轴矢量
8
④空间反演:
r
r
的操作称为对原点O
的空间反演。
x x
直角坐标系中的空间反演 y y
z z
空间反演不变的系统具有对O的点对称性。
例如,立方体对其中心具有点对称性。
反映空间反演对称性的物理量叫宇称(parity)。
轴对称
(b)
(c)
一次轴(对称) 四次轴(对称)
对转动操作状态不变的系统具有转动对称性。
对绕空间一固定点作任意旋转都不变的系统
具有球对称性。
5
③镜象反射:相当于“照镜子”的变换。
左右 反 射 面
上
下· ·
反射面
·左 右
x′ x
左手
右手
坐标
坐标
z′
·
y′
·y
z
反射面
反射面
(a)
(b)
(c)
上下、左右均对称 只左右对称 坐标系反射
