4-1多姿多彩的图形练习题及答案
2020年人教版七年级数学上册 课时作业本22 图形认识初步-多姿多彩的图形(含答案)

四、解答题 23.右图是一个正方体盒子的侧面展开图,该正方体六个面上分别标有不同的数字,且相对两
个面上的数字是一对相反数. (1)请把-10,8,10,-3,-8,3 分别填入六个小正方形中.
(2)若某相对两个面上的数字分别满足关系式
,求
24.八一体育馆设计一个由相同的正方体搭成的标志物(如图 5 所示),每个正方体的棱长为 1 米,其暴露在外面的面(不包括最底层的面)用五夹板钉制而成,然后刷漆.每张五夹板 可做两个面,每平方米用漆 500 克. (1)建材商店将一张五夹板按成本价提高 40%后标价,又以 8 折优惠卖出,结果每张仍 获 利 4.8 元(五夹板必须整张购买): (2)油漆店开展“满 100 送 20,多买多送的酬宾活动”,所购漆的售价为每千克 34 元.试问购买五夹板和油漆共需多少钱?
设五夹板 的进价为 元/张,根据题意得:(1+40%)× - =4.8,解得 =40(元), 购五夹板需付费:40×38=1520(元),购油漆应付费:34×37 .5=1275(元),
购油漆实际付费:1275-1200×
+1035 =25 55(元). 答:略.
=1035(元),因此购五夹板和油漆共需费用:1520
16.有一正方体木块,它的六个面分 别标上数字 1—6,下图是这个正方体木块从不同面所观察 到的数字情况。数字 2 对面的数字是
17.一个几何体的主视图和俯视图如图所示,若这个几何体最多有 m 个小正方体组成,最少有 n 个小正方体组成,m+n= .
18.一几何体的三视图如图所示,其中正视图与左视图是两个全等的等腰三角形,俯视图是 圆,则该几何体的侧面积为 .
12.若干桶方便面摆放在桌面上,如图所给出的是从不同方向看到的图形,从图形上可以看出 这堆方便面共有 桶.
4.1多姿多彩的图形练习题及答案

4.1多姿多彩的图形测试题 班级 姓名一、选择题1. 在下列立体图形中,不属于多面体的是( )A .正方体B .三棱柱C .长方体D .圆锥体2.若一个立体图形的正视图、左视图都是长方形,俯视图圆,则这个图形可能A .圆柱B 球C 圆锥D 三棱锥3.用平面去截下列几何体,不能截出三角形的是( )A .长方体B .三棱锥C . 圆柱D .圆锥4.你看这位可爱吧!表面展开平面图形是的是 ( ) A . 圆柱 B . 棱锥 C 圆锥 D. 球5.如图是一个正方形盒的展开图,若在其中的三个正方形A 、B 、C 、内分别填入适当的数,使得它们折成正方形后相对的面上的两个数互为相反数,则填入正方形A 、B 、C 内的三个数依次为 ( )A. 1,2-,0B. 0,2-,1C. 2-,0,1 D 2-,1,06.从不同的方向观察如图所示的实物几何体,不可能看到的视图( )7.将一个直角三角形绕它的最长边(斜边)旋转一周,得到的几何体是( )8.下列图形经过折叠不能围成三棱柱的是( )8.分别从正面、左面、上面看下列立体图形,得到的平面图形都一样的是( )10. 小丽制作了一个对面图案均相同的正方体礼品盒(如下左图所示),则这个正方体礼品盒的平面展开图可能是( ).二.填空题1.棱柱的面与面相交成_________;点动成 ;线动成________;面动成______;2.根据下列多面体的平面展开图,填写多面体的名称.(1)_________,(2)_________,(3)_______.3. 指出右面的三个图形分别是左面这个物体从哪个方向看到的图形.4.图中的几何体由 个面围成,面和面相交形成 条线,线与线相交形成 个点. 5.如图,六个大小一样的小正方形的标号分别是A ,B ,…,F ,它们拼成如图的形状,则三对对面的标号分别是 、 、 。
6.观察图中的几何体,指出右面的三幅,分别是从哪个方向看得到。
(1)是 ,(2)是 ,(3)是 。
第四章-多姿多彩的图形解答题

⊙ 班 级: 姓 名: 考 场: 学 号: ⊙⊙……………⊙……………装…⊙……………订……⊙………线………⊙……………装…⊙……………订……⊙………线…………⊙……………⊙第四章《多姿多彩的图形》解答题1、如图,∠AOB =900,∠COD =900,OC 平分∠AOB ,∠DOE =∠BOD 求: ∠COE 的度数。
2、 如图,于点是的平分线,求的度数.3、已知:AB=10,AC=6 ,点D是线段BC的中点,求CD的长.4、在地面上,有若干个完全相同的正方体堆成的一个几何体,请画出这个几何体的三视图。
(1)(2)5、已知:∠BOC=70°,∠AOC=50°,OD平分∠BOC,OE平分∠AOC.求:∠DOE的度数;6、已知:∠AOB=900, ∠COD=900, OC平分∠AOB,∠DOE=31∠BOD求:∠DOE的度数E ABCDO7、如图,延长线段AB 到C,使BC=3AB,点D 是线段BC 的中点,如果CD=3㎝,那么线段AC 的长度是多少?8、如图,已知AOB 为直线,OC 平分∠AOD ,∠BOD=50°, 求:∠AOC 的度数.A B CDO⊙ 班 级: 姓 名: 考 场: 学 号: ⊙⊙……………⊙……………装…⊙……………订……⊙………线………⊙……………装…⊙……………订……⊙………线…………⊙……………⊙9、如图,∠FOD=900,∠EOF=19°,OE 是∠AOD 的平分线求:∠AOD 的度数10、已知:AB=18,C 是AB 的中点,D 是AC 的中点,E 是BC 的中点。
求:DE 的长OABCEF 11、如图所示,︒=∠90AOB ,OE 平分AOB ∠、OF 平分BOC ∠,如果︒=∠60EOF ,求BOC ∠的度数.12、一个角的余角比它的补角的13还少20°, 求这个角的度数.13、已知∠α与∠β互余,且∠α比∠β小25°,求∠β的度数。
人教2012版数学第四章几何图形初步第09讲多姿多彩的图形

第09讲多姿多彩的图形考点·方法·破译1.会识常见的几何图形,并了解它们的名称.2.会画基本几何体(直棱柱、圆柱、圆锥、球)的三视图,会判断简单物体的三视图,以根据三视图描述基本几何体或实物原型.3.了解基本几何体与其三视图、展开图之间的关系.经典·考题·赏析【例1】根据下图回答问题(1)请说出①~⑥中几何体的名称,并简要叙述它们的一些特征.(2)将①~⑥中的几何体分类.【解法指导】认识几何体,以直观观察为主,一般特征也以观察者获得的形象加以表述即可.但对几何体尽可能地进行深入观察,全方位发现每个几何体的特征,从而逐步揭示其本质.解:(1) ①圆柱:特征如,两个底面是圆的几何体.②圆锥:特征如,像锥体,且底面是圆.③正方形:特征如,所有面都是正方形.④长方体:特征如,其侧面均为长方形.⑤棱柱:特征如,底面为多边形,侧面为长方形.⑥球:特征如,圆的实体.(2) ①③④⑤为一类,它们都是柱体.②是一类,它是锥体.⑥是一类,它是球体.【变式题组】01.下图四个几何体分别为长方体、圆柱体、球、三棱柱,这四个几何体中有三个从某个角度看到的图形都是一种几何图形,则另一个几何体是( )02.下列物体的形状类似于球体的是( )A.茶杯B.羽毛球C.乒乓球D.白炽灯泡03.用平面去截下列几何体,截面的形状不可能是圆的几何体是( )A.球B.圆锥C.圆锥D.正方体04.如图,立方体各面上的数字是连续的整数,如果相对的两个面上的两个数的和都相等,那么这三对数的总和是( )A.76 B.78 C.80 D.81 151411【例2】如图所示,仔细观察图中的两个物体,则它的俯视图是( )正面A.B.C.D.【解法指导】注意结合立体图形的形状并注意从某一方向看到图形的对应关系,抓住其主要特征,同时要分清不同视图的异同.故选择A.【变式题组】01.由四个大小相同的正方体组成的几何体如图所示,那么它的俯视图是( )A.B.C.D.02.如图,这个几何体从上面看到的平面图形是( )03.如图所示,圆柱从上面看到的图形是图中的( )04.如图是由一些完全相同的小立方块搭成的几何体从正面、左面、上面看到的图形,那么搭成这个几何体所用的小立方块的个数是( )A.3个B.6个C.7个D.8个从正面看从左面看从上面看【例3】将如右图所示的Rt△ABC绕直角边BC旋转一周,所得几何体从左面看到的是( )【解法指导】以直角三角形的直角边AC、BC为旋转轴得到的都是圆锥,故选择A.【变式题组】01.将右图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )02.若一个棱柱有12个顶点,则在下列说法正确的为( )A.这个棱柱有5个侧面B.这个棱柱有5条侧棱C.这个棱柱的底面是六边形D.这个棱柱的是一个12棱柱03.四棱柱的顶点数、棱数、面数分别为( )A.8,12,6 B.8,10,6 C.6,8,12 D.8,6,12 【例4】观察下列图形,其中不是正方体的展开图的为( )A.B.C.D.【解法指导】学习立体图形的展开图,要养成动手实验的好习惯,动手折一下往往会一目了然,故本题选择D.【变式题组】01.一个无盖的正方体盒子的平面展开图可以是下图中的( )A.只有图①B.图①、图②C.图②、图③D.图①、图③①②③02.如图所示的是一个由白纸拼成的立体图形,但有两面刷上黑色,将该立体图形展开后应该是( )A.B.C.D.03.下面四个图形中,经过折叠能围成如图只有三个面上印有图案的正方体盒的是( )A.B.C.D.04.如图所示是三棱柱纸盒,在下面四个图中,只有一个是这个纸盒的展开图,那么这个展开图是( )A.B.C.D.【例5】一个画家有14个边长为1米的正方体,他在地面上把它们摆成如右图的形状,然后他把露出的表面涂上颜色,那么被涂上颜色的总面积为( )A.19平方米B.21平方米C.33平方米D.34平方米【解法指导】本题把涂上颜色的面积一块一块加起来计算很麻烦,应从整体角度出发,把立体转化为平面,观察题图所给的几何体,从前、后、左、右四个方向都只能看到6个1×1的正方形,从上面看可以看到一个3×3的大正方形轮廓,所以被涂上颜色的总面积应为4×6×1×1+3×3×1×1=33(平方米),故选C.【变式题组】01.如图是由若干个大小相同的小正方体堆砌而成的几何体.那么其三种视图中面积最小的是( )A.正视图B.左视图C.俯视图D.三种一样02.将一个底面直径为2 cm,高为2 cm的圆柱形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )A.2πcm2B.3πcm2C.4πcm2D.5πcm203.一个大长方体是由四个完全一样的小长方体拼成的,如果每个小长方体的长、宽、高分别是3, 1,1那么这个大长方体的表面积可能有______种不同的值,其中最小值为______.【例6】李明为好友制作一个(右图)正方形礼品盒,六个面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )【解法指导】 本例主要考查立方体的展开图中对面、邻面的分布规律,可动手折叠发现答案,故应选择C .【变式题组】 01.已知一个正方体的每一面都填有唯一一个数字,且各相对面上所填的数互为倒数,若这个正方 体的平面展开图如右图所示,则A 、B 的值分别是( )A .13,12B . 13,1C .12,13D .1,1302.在下图中添加一个小正方形,使该图经过折叠后能围成一个四棱柱,不同的添法共有( )A .7种B .4种C .3种D .2种03.将一张长与宽的比为2:1的长方形纸片按如图①、②所示的方式对折后,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是()【例7】 设5 cm ×4 cm ×3 cm 长方体的一个表面展开图的周长为n cm ,则n 的最 小值是______.【解法指导】 把展开图的周长用相应的代数式表示.长方体的展开图的周长为8c +4b +2a .故周长最小值为8×3+4×4+2×5=50,故填50 cm .【变式题组】01.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,如图现有一个边长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?BA 312102.如图是几个小立方块所搭成的几何体.从上面看图形,小正方形中的数字表示该位置的小立方块的个数,那么是这个几何体从正面看的图形的是( )2211A.B.C.D.03.如图①是由若干个小正方体所搭成的几何体,②是①从上面看到的图形,则①从左面看到的图形是( )①②A.B.C.D.演练巩固反馈提高01.水平位置的下列几何体,从正面看的图形不是长方形的是( )02.有一个外观为圆柱形的物体,它的内部构造从外部看不到,当分别用一组平面沿水平方向(自上而下)和竖直方向(自左而右)截这个物体时(如图),得到了如图所示的(1)、(2)两组形状不同的截面,则这个物体的内部构造是( )A.空心圆柱B.空心圆锥C.空心球D.空心半球03.将如图所示图形折叠成立方体后,下面四个选项正确的是( )04.由一些大小相同的小正方体组成的几何体的俯视图如图所示,其中正方形的数字表示在该位置上的小正方体的个数,那么,这个几何体的左视图是( )21231A .B .C .D .05.一个几何体的三视图如图所示,那么这个几何体是()A .B .C .D .06.如图,下列四个几何体中,其主视图、左视图、俯视图中只有两个相同的是( )07.如下图所示的某一几何体的三视图,则这个几何体是( )A .圆柱B .圆锥C .正方体D .球 正视图 左视图 俯视图08.如图是一个几何体的三视图,根据图中提供的数据(单位: cm )可求得这个几何体的体积为 ( ) A .2 cm 2 B .4 cm 2 C .6 cm 2 D .8 cm 2 主视图 左视图 俯视图12 121109.如图所示是无盖长方体盒子的表面展开图(重叠部分不计)则盒子的容积为( )A .4B .6C .12D .1510.宜黄素有“华南虎之乡”的美誉,将“华南虎之乡美”六个字填写在一个正方体的六个面上,其平面展开图如图所示,那么在该正方体中,和“虎”字相对的字是______.11.如图是由棱长为1的正方体搭成的积木三视图,则图中棱长为1的正方体的个数是______.主视图左视图俯视图12.设有一个边长为1的正三角形,记作A1,将A1的每条边三等分,在中间的线段上向外作正三角形,去掉中间的线段后所得到的图形记作A2;将A2的每条边三等分,重复上述过程,所得到的图形记作A3,现将A3的每条边三等分,重复上述过程,所得到的图形记作A4,则A4的周长是多少?14.由3个相同的小立方块搭成的几何体如图所示,请画出它的主视图和俯视图.主视方向15.一个五棱柱如图,它的底面边长都是4厘米,侧棱长6厘米,回答下列问题.(1)这个五棱柱一共有多少个面?它们分别是什么形状?哪些面的形状、面积完全相同?(2)这个五棱柱一共有多少条棱?它们的长度分别是多少?美乡之虎南华培优升级 奥赛检测01.如图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,那么该几何体的从正面看到的图形为( )211423A .B .C .D .02.将圆柱形纸筒沿母线AB 剪开铺平,得到一个矩形(图1);如果将这个纸筒沿线路BMA (图2)剪开铺平,得到的图形是( ) A .平行四边形 B .矩形 C .三角形 D .半圆03.一根单线从纽扣的4个孔中穿过(每个孔只穿过一次),其正面情形如图所示,下面4个图形可能 是其背面情形的是( )04.用M 、N 、P 、Q 各代表四种简单几何图形(线段、正三角形、正方形、圆)中的一种,下图①至④是由M 、N 、P 、Q 中的两种图形组合而成的(组合用“&”表示).那么下列组合图形表示P &Q 的是 ( )05. 如图是一个立体图形的主视图,左视图(图中单位为厘米),则立体图形的体积为( )立方厘米. A .π B .2π C .3π D .4π06.如下左图是一个正方体的平面展开图,这个正方体是()A.B.C.D.07.把10个相同的小正方形按如图的位置堆放,它的外表会有若干个小正方形,如果将图中标有字母P的一个小正方体搬去,这时外表含有的小正方形的个数与搬运前相比( )A.不增不减B.减少1个C.减少2个D.减少3个08.如图,可以沿线折叠成一个带数字的立方体,每三个带数字的面交于立方体的一个顶点,则相交于一个顶点的三个面上的数字之和最小值是______.09.设5 cm×4 cm×3 cm长方体的一个表面展开图的周长为n cm,则n的最小值是______.10.已知直四棱柱的底面是边长为a的正方形,高为h,体积为V,表面积等于S.(1)当a=2,h=3时,分别求V和S;(2)当V=12,S=32时,求2a+1h的值.P654321。
4.1多姿多彩的图形

4.2.1 直线 射线 线段——定义及表示 序号:50七 年级备课人: 审核: 审批: 班级:____________ 姓名:____________ 时间: 年 月一、导学目标知识点:理解定义及表示方法,正确画图,领悟三者之间的区别与联系.二、课时:1课时三、导学方法:先学后教,当堂训练四、导学过程:1、课前导学:(1)通读教材: (2)回答问题:①做标记; ①点与直线有几种位置关系?画图说明②找要点; ②直线的性质是________________________,举例说明应用.2、课堂导学:(1)直线的性质(公理): “确定”的意义:(2)相交线的定义:性质:(3)直线、射线、线段表示画图注意事项.3、题例导练:例1,已知A 、B 、C 、D 四点按语句画图①画线段AB ,射线AD ,直线AC ;②连接BD 与直线AC 交于E ;③连接BC 并延长线段BC 与射线AD 交于F ;④连接CD ,并延长CD 与线段AB 的反向延长线交于点C.例2,已知数轴上A 、B 对应的数分别为3、23-①数轴是什么图形?②数轴在原点O 两边的(含O 点)分别是什么图形,如何表示? ③射线OA 上的点(含O )表示什么数?端点呢?④数轴上表示不小于23-且不大于3的部分表示什么图表?如何表示?五、课堂练习:1、平面上有A 、B 、C 三点,过其中的每两点画直线,最多可以画_________条直线,最少可以画_________条直线.2、如图,在直线l 上取任意4点,数一数图中共有线段_________条,共有射线________条.3、下列叙述中正确的是( )①线段AB可表示为线段BA;②射线AB可表示为射线BA;③直线AB可表示为直线BA;④线段、射线、直线都可以用字母a表示A、①②③B、②③④C、①③④D、①②④4、手电筒发射出来的光线,给我们的印象似()A、线段B、直线C、射线D、都有可能5、如图所示的直线、射线、线段能相交的是()6、农民兴修水利,开挖水渠,先在两端立桩拉线,然后沿线开挖,其中的数学道理是____________________.7、如图中共有不同的线段__________条,不同的射线_________条.8、平面内三条直线两两相交,最多可将平面分成________部分,最少分为__________部分.9、下列语句中能正确表达图的特点的个数是()①直线l经过A、B两点;②A、B两点都在直线上③l是A、B两点确定的直线;④l是一条直线,A、B是任意一点A、4B、3C、2D、110、如图所示,从A地到C地,有走水路、走陆路、走空中三种方式.从A地到B地有2条水路和3条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直接到达C地,则从A地到C地可供选择的方案有()A、20种B、8种C、5种D、16种11、生活数学往返于A、B两地的客车,中途要停靠三个站.问:(1)有多少种不同票价?(2)要准备多少种车票?课后反思:小组评价:教师评价:4.2.2 直线 射线 线段—线段的比较与和差 序号:51七 年级备课人: 审核: 审批: 班级:____________ 姓名:____________ 时间: 年 月一、导学目标知识点:掌握两种比较方法,领悟比较的意义,正确进行和差计算.二、课时:1课时三、导学方法:先学后教,当堂训练四、导学过程:1、课前导学:(1)通读教材(2)回答问题 ①找要点;①线段大小比较的两种方法:1、___________;2、__________. ②做标记;②线段大小比较结果会出现几种情况,画图说明. ③想联系.③当两线段不等时,试结合图形,找出线段及其和差的相等关系. ④如何作一线段等于已知线段. 2、课堂导学作一线段等于已知线段截取法(圆规的使用)度量法3、题例导练例1,已知线段a 、b (a>b ),求作线段AB ,AB=2a-b例2,画线段AB=6cm ,在直线AB 上截取线段BC=2cm ,求AC=?五、课堂练习:1、已知线段MN=8cm ,MP=3cm ,再添加一个条件:_________,就一定可以得出,P 在直线MN 上.2、如图,CB=31AB ,AB=31AD ,如果CB=2cm ,则线段AD 的长为________cm.3、下面给出的四条线段中,最长的是( )4、如图,延长线段AB 到C ,使BC=4,若AB=8,则线段AC 的长是BC 的_______倍.5、如图,AN=MD ,则AM 与ND 的大小关系是( )A 、AM >NDB 、AM <NDC 、AM=ND D 、无法确定6、下列说法中,正确的是( )A 、延长射线OAB 、作直线AB 的延长线C 、延长线段AB 到C ,使AC=21AB D 、延长线段AB 到C ,使AC=2AB7、开发题已知线段AC=2,BC=3,则线段AB 的长度是( )A 、5B 、1C 、5或1D 、非以上答案甲同学答: AB=AC+BC=5 选A.乙同学答: AB=BC-AC=1,选C.你认为谁做的对,你的答案是什么?并说明理由.8、如图,A 、B 、C 、D 是直线l 上的顺次4点且线段AC=5cm ,BD=4cm ,则线段AB-CD 的 差等于_________cm.课后反思:小组评价: 教师评价:。
初一上册_图形测试题附答案
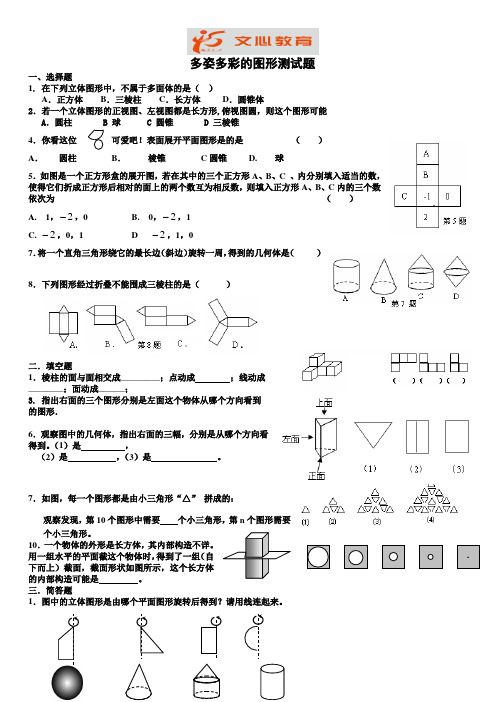
多姿多彩的图形测试题一、选择题1. 在下列立体图形中,不属于多面体的是( )A .正方体B .三棱柱C .长方体D .圆锥体2.若一个立体图形的正视图、左视图都是长方形,俯视图圆,则这个图形可能 A .圆柱 B 球 C 圆锥 D 三棱锥4.你看这位可爱吧!表面展开平面图形是的是 ( )A . 圆柱B . 棱锥C 圆锥 D. 球5.如图是一个正方形盒的展开图,若在其中的三个正方形A 、B 、C 、内分别填入适当的数,使得它们折成正方形后相对的面上的两个数互为相反数,则填入正方形A 、B 、C 内的三个数依次为 ( ) A. 1,2-,0 B. 0,2-,1 C. 2-,0,1 D 2-,1,07.将一个直角三角形绕它的最长边(斜边)旋转一周,得到的几何体是( )8.下列图形经过折叠不能围成三棱柱的是( )二.填空题1.棱柱的面与面相交成_________;点动成 ;线动成________;面动成______;3. 指出右面的三个图形分别是左面这个物体从哪个方向看到的图形.6.观察图中的几何体,指出右面的三幅,分别是从哪个方向看得到。
(1)是 , (2)是 ,(3)是 。
7.如图,每一个图形都是由小三角形“△” 拼成的:观察发现,第10个图形中需要 个小三角形,第n 个图形需要 个小三角形。
10.一个物体的外形是长方体,其内部构造不详。
用一组水平的平面截这个物体时,得到了一组(自下而上)截面,截面形状如图所示,这个长方体的内部构造可能是 。
三.简答题1.图中的立体图形是由哪个平面图形旋转后得到?请用线连起来。
3.如图,左面的几何体叫三棱柱,它有五个面,9条棱,6个顶点,中间和右边的几何体分别是四棱柱和五棱柱。
(1)四棱柱有 个顶点, 条棱, 个面;(2)五棱柱有 个顶点, 条棱, 个面;(3)你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗? (4)那么n 棱柱呢?2.下列关于角的说法正确的是( ).A .两条射线组成的图形叫做角;B .延长一个角的两边;C .角的两边是射线,所以角不可以度量;D .角的大小与这个角的两边长短无关 4.如图所示,能用∠AOB ,∠O ,∠1三种方法表示同一个角的图形是( ).7.下列各角中,是钝角的是( ). A .14周角 B .23周角 C .23平角 D .14平角 10.已知∠α=18°18′,∠β=18.18°,∠γ=18.3°,下列结论正确的是( ).A .∠α=∠βB .∠α<∠βC .∠α=∠γD .∠β>∠γ11.(1)把周角平均分成360份,每份就是_____的角,1°=_____,1′=_______. (2)25.72°=______°______′_______″. (3)15°48′36″=_______°. (4)3600″=______′=______°.12.如图所示,将一个矩形沿图中的虚线折叠,请用量角器测量一下其中的α,β,得α________β. 13.计算下列各题:(1)153°19′42″+26°40′28″ (2)90°3″-57°21′44″(3)33°15′16″×5 14.(1)1点20分时,时钟的时针与分针的夹角是几度?2点15分时,•时钟的时针与分针的夹角又是几度? (2)从1点15分到1点35分,时钟的分针与时针各转过了多大角度?(3)时钟的分针从4点整的位置起,按顺时针方向旋转多少度时才能与时针重合?16.如图所示,指出OA 是表示什么方向的一条射线,•并画出表示下列方向的射线: (1)南偏东60°;(2)北偏西70°;(3)西南方向(即南偏西45°)A C D B1、在同一平面内,两条直线的可能位置关系是( )A 、平行B 、相交C 、平行和垂直D 、平行或相交 3、下列说法正确的是( )A 、两条射线组成的图形叫做角B 、射线就是直线C 、小于平角的角可分为锐角和钝角两类D 、两点之间,线段最短 4、下列关于作图的语句中正确的是( )A 、画直线AB =10厘米;B 、画射线OB =10厘米;C 、已知A 、B 、C 三点,过这三点画一条直线;D 、过直线AB 外一点画一条直线和直线AB 平行。
多姿多彩的图形世界专题训练

|
毒
1 在生 活 中只要 你 注 意观 察 。就会 发 现 类 似 。 几何 体 的物 体 无 处 不 在 . 过 观 察 , 你 把 通 请 下 面实 物 以及 与 其对 应 的 几何 体 用 线 段 连 接起 来.
主 视 图
7 下 图是 一个食 品包装 盒 的侧 面展 开 图. .
3霉给外的 , 。 她 礼图 ” 婆 盒 阳送 节
中所示礼 盒的主视图是 ( ) . 第3
第 7题 图
匿圈
A. B. C. D.
( ) 写 出 这 个 包 装 盒 的 多 面 体 形 状 的 1请
名称 :
‘ . ‘
,足 C 中点 . C.
CD : 8,‘4 : 8,’ =2, . x . . .
4I
.
C Dl 1
。 .
.
AD =9 x= l . 8
/ /
l 詹 C D
D
・ .
・
是 A 的 中点 , D
.
.
.
^ : D— £:LA C , M c) c D— D:. 8 8 . 1 _×1 — :1
Sef o ue ti h r a e to l vc oi s l -c nq s st eg e t s fal it re .
一 一 一 ~ 一 一 一 一 一 一
, , ,,
,
,
『 ,
2 3
征 服 自己是 一 切 胜 利 中之 最 伟 大者 。— — 柏 托 图
例 3设 AB=2 , 由 A B C =2: 4 x B: C: D 3: ,得 B C: 3 , D=4 . xC x AD:( +3+4 x=9 . 2 ) x
多姿多彩的靠垫

多姿多彩的靠垫(1)
1 我们的靠垫既美观又舒适
2
看了这么多,也说了这么多,你们想不想动手为自己设计 一 接个 下只 来属 同于 学你 们一 来个和人老的师靠一垫起呢看一? 看接下来的课件,哪些靠
垫是对称的?那他们是哪种对称式呢?很好,图一这种叫
3
自由纹样,图二左右花纹一样,叫轴对称图形,接下来我 们观看一段用剪纸演示轴对称图形的视频~那么这个图三
了他们是如何设计的,欣赏完其他同学的作品
多姿多彩的靠垫(1)
同学们应该都跃跃欲试 了吧,现在我们来设计
属于你们的最美靠垫 吧!
首先我们要先和老师完 成一个任务清单1、 你 想为什么样的房间或为 谁设计靠垫?
2、 你想设计什么形 状的靠垫?
PART 1
3、 你想利用什么对称型来设计 靠垫花纹?A轴对称B中心对称
同学们刚才都太好了,真是火眼金睛,看到 了这么多不同图案和形状的靠垫,那我们能 不能用一个词来概括一下它们?
我听到同学们异口同声地说是靠垫
现在我要考一考大家,我随机拿起一个靠垫, 谁能马上说出它的外形、图案、色彩适合放 在什么地方? 说得可真细致,很棒,那我换一个,你说这 是圆形的,小狗图案,红色的,放在卧室刚 好
呢以花朵为中心,蝴蝶围绕花朵做重复运动,我们把这种
叫 同做 学中 们心 ,对 我称 们可以和老师一起准备一张正方形的纸,我们
4
来看一看课件,你知道上面的图案是什么骨式吗?那我们 把单个图案放进相应的骨式里,根据骨式里的线条放进图
案
你还有其他的摆放方法吗?接下来我们来和老师一起看看
5 我是如何制作的吧,我们刚才欣赏了老师的作品,也感受
这节课我们就一起学习多姿多彩的靠垫
多姿多彩的靠垫(1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.1多姿多彩的图形测试题
一、选择题
1. 在下列立体图形中,不属于多面体的是( )
A .正方体
B .三棱柱
C .长方体
D .圆锥体
2.若一个立体图形的正视图、左视图都是长方形,俯视图圆,则这个图形可能 A .圆柱 B 球 C 圆锥 D 三棱锥
3.用平面去截下列几何体,不能截出三角形的是( )
A .长方体
B .三棱锥
C . 圆柱
D .圆锥 4.你看这位可爱吧!表面展开平面图形是的是 ( ) A . 圆柱
B . 棱锥
C 圆锥
D. 球
5.如图是一个正方形盒的展开图,若在其中的三个正方形A 、B 、C 、内分别填入适当的
数,使得它们折成正方形后相对的面上的两个数互为相反数,则填入正方形A 、B 、C 内的三个数依次为 ( )
A. 1,2-,0
B. 0,2-,1
C. 2-,0,1 D 2-,1,0
6.从各个不同的方向观察如图所示的实物几何体,不可能看到的视图是( )
7.将一个直角三角形绕它的最长边(斜边)旋转一周,得到的几何体是( )
8.下列图形经过折叠不能围成三棱柱的是( )
9.分别从正面、左面、上面看下列立体图形,得到的平面图形都一样的是( )
10.小丽制作了一个对面图案均相同的正方体礼品盒(如下左图所示),则这个正方体礼品盒的平面展开图可能是().
二.填空题
1.棱柱的面与面相交成_________;点动成;线动成________;面动成______;
2.根据下列多面体的平面展开图,填写多面体的名称.
(1)__________, (2)__________, (3)_________.
3. 指出右面的三个图形分别是左面这个物体从哪个方向看到的图形.
4.图中的几何体由个面围成,面和面相交形成条线,线与线相交形成个点.5.如图,六个大小一样的小正方形的标号分别是A,B,…,F,它们拼成如图的形状,则三对对面的标号分别是、、。
6.观察图中的几何体,指出右面的三幅,分别是从哪个方向看得到。
(1)是,(2)是,(3)是。
7.如图,每一个图形都是由小三角形“△” 拼成的:
观察发现,第10
个图形中需要 个小三角形,第n 个图形需要 个小三角形。
8
.下面三个图形中,图形 可以用平面截长方体得到,图形 可以用平面截圆锥得到,图形 可以用平面截圆柱得到。
9.将标号为A 、B 、C 、D 的正方形沿图中的虚线剪开后得到的标号为P 、Q 、M 、N 的四组图形,试按照“哪个正方形剪开后得一哪组图形”的对应关系填空.(4分)
A 与______对应;
B 与______对应;
C 与_______对应;
D 与________对应.
10.一个物体的外形是长方体,其内部构造不详。
用一组水平的平面截这个物体时,得到了一组(自下而上)截面,截面形状如图所示,这个长方体的内部构造可能是 。
三.简答题
1.图中的立体图形是由哪个平面图形旋转后得到?请用线连起来。
(1) (2) (3)
2.如图六个平面图形中,有圆柱、圆锥、三棱柱(它的底面是三边相等的三角形)的表面展开图,请你把立体图形与它的表面展开图用线连起来.
3.如图,左面的几何体叫三棱柱,它有五个面,9条棱,6个顶点,中间和右边的几何体分别是四棱柱和五棱柱。
(1)四棱柱有个顶点,
条棱,个面;
(2)五棱柱有个顶点,条棱,个面;
(3)你能由此猜出,六棱柱、七棱柱各有几个顶点,几条棱,几个面吗?
(4)那么n棱柱呢?
4.如图是一个长方体的表面展开图,每个面上都标注了字母,请根据要求回答问题:(1)如果A面在长方体的底部,那么哪一个面会在上面?
(2)如果F面地前面,B面在左面,那么哪一个面会在上面?(字母朝外)
(3)如果C面在右面,D面在后面,那么哪一个面会在上面?(字母朝外)
5. 课桌上按照右图的位置放着一个暖水瓶、一只水杯和一个乒乓球.小明从课桌前走过(图中虚线箭头的方向),图.-13描绘的是他在不同时刻看到的情况,请对这些图片按照看到的先后顺序进行排序:正确的顺序是:
、 、 、 .
6. (本题6分)如图是一座简易的工房分别从正面、上面和左面看所看到的图形,你能想象出这座简易工房的样子吗?请把它画出来.
甲 丙
丁 乙 水
杯 乒乓
球
暖水瓶
参考答案
一.选择题
二.填空题
1. 线、线、面、体;
2. 长方体、三棱柱、三棱锥(四面体);
3. 上、正、左;
4. 9、16 、8 ;
5. A与F 、B与D、E与C ;
6. (1)上(2)正(3)左;
7. 100、2n;
8.(1)(2)、(1)(3)、(3); 9. M、P、Q、N; 10. 圆锥
三.简答题
1.
2.
3.(1).8、12、6;(2).10、15、7;(3).六棱柱有12个顶点,18条棱,9个面;七棱柱有14个顶点,21条棱,9个面;(4).n棱柱有2n个顶点,3n条棱,(n+2)个面.
4.(1)F;(2)C;(3)A
5. 乙→甲→丙→丁
6.图略(画的只要符合条件既可,特别美观者可以另外加分)。
