2010陈省身杯数学邀请赛六年级答案
第一届至第九届(2010-2018年)陈省身杯全国高中数学奥林匹克试题及答案【PDF版】

第九届陈省身杯全国高中数学奥林匹克1.已知锐角△ABC 的外接圆为⊙O ,边BC 、CA 、AB 上的高的垂足分别为D 、E 、F ,直线EF 与⊙O 的 AB 、AC 分别交于点G 、H ,直线DF 与BG 、BH 分别交于点K 、L ,直线DE 与CG 、CH 分别交于点M 、N .证明:K 、L 、M 、N 四点共圆,且该圆的直径为2222()b c a +-,其中,BC =a ,CA =b ,AB =c .证明 如图1,因为B 、C 、E 、F 四点共圆,所以,AFE ACB ∠=∠.图1°°2GB HA AFE 注意到,+∠=, °°°22AB AG GB ACB +∠==. 从而, HA AG =,即AG AH =.因为C 、A 、F 、D 四点共圆,所以,=BFD ACB AFE BFG ∠=∠∠=∠.从而,直线GH 与直线DK 关于直线AB 对称.由 °°AG AH =, 知GBA ABH ∠=∠.从而,直线BK 与直线BH 关于直线AB 对称.因此,点K 、H 关于直线AB 对称,即AK =AH .类似地:点L 、G 关于直线AB 对称,即AL =AG ;G 、N 关于直线AC 对称,即AG =AN ;M 、H 关于直线AC 对称,即AM =AH .综上,AL =AN =AG =AH =AK =AM .因此,K 、L 、M 、N 四点共圆,且圆心为A ,半径为AG ,记该圆为⊙A . 设⊙O 的半径为R ,⊙O 的直径AQ 与GH 交于点P .如图2.图2则∠AGQ=90°,且AP ⊥GH .由射影定理得2AG AQ AP =⋅.注意到,sin =cos sin AP AF AFE AC CAB ACB .=⋅∠⋅∠⋅∠2222222cos sin =22AQ AP R AC CAB ACBb c a b c a AB AC bc 故.⋅=⋅∠⋅∠+-+-=⋅⋅ 因此,2222b c a AG +-=,⊙A 的直径为2222()b c a +-.。
历届陈省身杯重要知识点-数论(答案)

六年级历届陈省身杯重要知识点数论专题高频考点一、05~10陈省身杯数论模块重要知识点约、倍、质、合、整除位值原则余数(中国剩余,同余)个位率常用方法1.翻译?!2.分解3.位值4.题型特点—方法(同余、奇偶性…)【例1】(2010年陈省身杯第4题)三个相邻的自然数的乘积是3360,这三个自然数分别是________、________和________。
5=⨯⨯⨯=⨯⨯,所以三个自然数为14、15、16。
33602357141516【例2】(2008年13题)用5、6、7、8四个数字(每个数字恰好用一次)可组成24个不同的四位数,其中有________个数能被11整除。
5+8=6+7,当奇数位是5、8时:2×2=4(种)。
当奇数位是6、7时:2×2=4(种)。
共有8(种)。
【例3】(2009年12题)A、B、C、D都是小于100的合数,并且A、B、C、D两两互质,则A+B+C+D的最大值为_______。
由于此题求和的最大值,所以我们要使每个数尽量大,且保证其两两互质,故分别取99,95,94,91,和为379。
【例4】(2011年4题)一个数是质数,+10 +14 都是质数,求这个数是几?这个数为3。
【例5】(2011年6题)A是大于0的最小自然数,B是质数中唯一的偶数,C是最小的奇质数,C和D的和是70,问:A+B×C×D×(B+C)=_______。
A=1,B=2,C=3,D=67;A+B×C×D×(B+C)=2011【例6】(2011年14题)有一个三位数,各个数位都不为0,且不相同,把这三个数交换位置,形成5个不同的三位数,其平均数为这三位数,求这三个数最大数多少?设此三位数为abc ,则形成的5个三位数在加上原数就是原数的6倍 则有:222()6a b c abc ++=,37()abc a b c =++;三位数各不相同,最大629符合要求。
小学数学《速算与巧算》练习题(含答案)

小学数学《速算与巧算》练习题(含答案)【复习1】(我爱数学夏令营)计算:6.11+9.22+8.33+7.44+5.55+4.56+3.67+2.78+1.89分析:原式=(6.11+1.89)+(9.22+2.78)+(8.33+3.67)+(7.44+4.56)+5.55=8+12+12+12+5.55=49.55【复习2】(06香港圣公会小学奥林匹克)计算:3.72-2.73+4.6+5.28-0.27+6.4分析:原式=(3.72+5.28)+(4.6+6.4)-(2.73+0.27)=9+11-3=17 .【复习3】(华罗庚学校五年级入学考试试题)8×(3.1-2.85)×12.5×(1.62+2.38)-3.27分析:初看这道题好像不能用简便方法进行计算.但是里面有特殊数8、12.5,所以可以先算一步,再用简便方法进行计算.原式=8×0.25×12.5×4-3.27=(8×12.5)×(0.25×4)-3.27=100-3.27=96.73【复习4】(04陈省身杯数学邀请赛)(56789+67895+78956+89567+95678)÷7分析:原式=(5+6+7+8+9)×11111÷7=5×11111=55555 . 观察可知5、6、7、8、9在万、千、百、十、个位各出现过一次 .【复习5】计算:l-2+3-4+5-6+…+2005-2006+2007分析:原式= l+3-2+5-4+7-6+…+2005+2007-2006=1+1×1003=1004 ,分组求和的思路.在速算的过程中,如果加入运算律的应用,会有意想不到的效果!我们一起先来看看常用的一些运算律和结论吧!在计算过程中,最常用的技巧之一是灵活熟练地运用运算律.运算律有:(1)加法交换律:a+b=b+a(2)加法结合律:(a+b)+c=a+(b+c)(3)乘法交换律:ab=ba(4)乘法结合律:(ab)c=a(bc)(5)分配律: a(b+c)=ab+ac (反过来就是提取公因数)(6)减法(括号)的性质:a-b-c=a-(b+c)(7)除法的性质:a÷(b×c)=a÷b÷c(a+b) ÷c=a÷c+b÷c(a-b) ÷c=a÷c-b÷c和不变的规律:如果一个加数增加另一个加数减少同一个数,它们的和不变.积不变的规律:如果一个因数扩大几倍,另一个因数缩小相同的倍数,积不变.商不变的规律:如果除数和被除数同时扩大或缩小相同的倍数,商不变.【例1】(04陈省身杯数学邀请赛)计算:3.1415×252-3.1415×152分析:(法1):题中的三项都有因数34.5,容易想到把34.5作为公因数提取出来(把乘法分配律反过来用),从而使计算简便.原式=34.5×(8.23+2.77—1)=34.5×10=345.(法2):原式=3.1415×(252-152)=3.1415×(25+15)×(25-15)=3.1415×40×10=1256.6 应用下面的平方差公式【回忆巩固】a、b代表任意数字,(a+b)×(a-b)=a×a-b×b,这个公式在数学上称为平方差公式。
6年级“陈省身杯”模拟答案

六年级“陈省杯”数学竞赛模拟题答案测试时间:60分钟 姓名 成绩一、填空 (每题7分。
)1、20072008×20082008-20072007×20082007=( 40154015 )2、2007年12月21日是星期五,北京奥运会将在2008年8月8日举行,试推算一下,那一天是星期( 五 )。
3、五个评委分别给一名参加“超级女声”歌咏大赛的选手评了分。
如果去掉一个最高分和一个最低分后,平均95.8分;如果去掉一个最低分平均96.6分;如果去掉一个最高分后平均94.6分。
这五个评委给的原始平均分是( 95.48 )分。
4、将12张卡片分给甲、乙、丙、丁4个人,每人3张,卡片分三种,红卡片值是5分、绿卡片值是2分、黄卡片值是1分,结果甲得6分,乙得11分,丙得9分,已知红卡片的张数与黄卡片相同,那么丁得到( 4 )分。
5、王辉和李奕都是IC 卡收集迷。
一天他们在一起整理好IC 卡后,王辉说:如果你给我12张,我们的卡就一样多。
李奕说,如果你给我12张,我的卡就是你的4倍。
他们一共收集了( 80 )张卡。
6、将3支红筷子,9支黄筷子,18支绿筷子和1支黑筷子混合放在一个布袋里,黑暗中至少摸出( 7 )支,才能保证有两双颜色相同的筷子。
7、右图三角形中,AB=4AD AC=5AE 已知四边形BCED 的面积是57平方厘米,那么小三角形ADE 的面积是( 3 )平方厘米。
8、数列的第一个数是4,后面的数规律是:如果前一个数小于(或等于)10,就将它乘以2;如果前一个数大于10,就将它减去7,这样一直写下去,数列的第2007个数是( 16 )。
9、某剧院有20排座位,后一排比一排多2个座位,最后一排有50个座位,这剧院共有( 620 )个座位。
10、1234567891011……383940是一列按一定规律排列的数字,现在要求从中划去61个 数字,使得剩下的数字(前后顺序不变)组成一个最大的多位数,这个多位数是( 9997383940 )。
2010年“陈省身杯”国际青少年数学邀请赛四年级试题

2010年“陈省身杯”国际青少年数学邀请赛四年级1. 计算17474719196634_____⨯+⨯+⨯+⨯=2. 十个连续自然数的和不大于100,这十个数的和最大是______。
3. “陈省身数学周”组委会为了奖励参加活动的学生,买来数学故事数和数学文化书共2010本,其中数学文化书是数学故事书的4倍,那么数学故事数有_____本。
4. 数学课上,李老师布置了两道题,结果有34人答对了第一题;有46人做对了第二题;没有人两道题全部做错。
如果这个班共有52人,那么两道题都做对的有_____人。
5. 为庆祝元旦,学校在大门口安装了50盏彩灯,彩灯按照“黄黄红绿绿红黄黄红绿绿红…”的顺序依次排列,则在这50盏彩灯中,共有黄色的彩灯_____盏。
6. 如图,观察这个数表并找出它的规律,这个数表第15行的第一个数是______。
(2523211917)16141210975421?身杯身省陈第6题图 第8题图 第9题图7. 2004年时,父亲的年龄是哥哥和弟弟年龄之和的4倍;而2010年时,父亲的年龄是哥哥和弟弟年龄之和的2倍,那么父亲出生在______年。
8. 在上面的方格表的每个小方格中填入一个字,使得方格表的每行、每列及每条对角线上的四个方格中的文字都是“陈”、“省”、“身”、“杯”,那么表中“?”所在的方格中应填的汉字是______。
9. 数一数,上图中共有_____个三角形。
10. 计算1(12)(123)(1234)(1298)(1299)_____-++++-++++-+++++++= 。
11. 将1、3、5、7、9、11、13、15、17这9个自然数填入到右图的圆圈中,使得每个正方形的四个角上的数字之和都相等,这个相等的和是_____。
12. A 、B 、C 、D 四名学生猜测自己的数学成绩。
A 说:“如果我得优,那么B 也得优。
”B 说:“如果我得优,那么C 也得优。
”C 说:“如果我得优,那么D 也得优。
2010陈省身杯数学邀请赛四年级答案

2010年“陈省身杯”国际青少年数学邀请赛四年级1. 计算17474719196634_____⨯+⨯+⨯+⨯=分析:1747471919663447171961934=4736653=4766653=2826653=282+536=3356=2010⨯+⨯+⨯+⨯=⨯++⨯+⨯+⨯⨯⨯+⨯⨯+⨯⨯⨯()()()2. 十个连续自然数的和不大于100,这十个数的和最大是______。
分析:和=(首项+尾项)×项数÷2=(首项+尾项)×10÷2=(首项+尾项)×5和是5的倍数,所以最大为953. “陈省身数学周”组委会为了奖励参加活动的学生,买来数学故事数和数学文化书共2010本,其中数学文化书是数学故事书的4倍,那么数学故事数有_____本。
分析:和倍问题。
数学故事书有2010÷(4+1)=402(本)4. 数学课上,李老师布置了两道题,结果有34人答对了第一题;有46人做对了第二题;没有人两道题全部做错。
如果这个班共有52人,那么两道题都做对的有_____人。
分析:容斥原理。
则两道题都做对的有 34+46-52=28(人)5. 为庆祝元旦,学校在大门口安装了50盏彩灯,彩灯按照“黄黄红绿绿红黄黄红绿绿红…”的顺序依次排列,则在这50盏彩灯中,共有黄色的彩灯_____盏。
分析:周期问题。
可以找到是按照“黄黄红绿绿红”的顺序循环,6个一循环,即周期是6.那么50÷6=8…2,有8个这样的循环多两个黄灯,一个循环中有2个黄灯,那么共有黄灯8×2+2=18(盏)6. 如图,观察这个数表并找出它的规律,这个数表第15行的第一个数是______。
(2523211917)16141210975421?身杯身省陈第6题图 第8题图 第9题图分析:发现这个数表的奇数行是奇数,偶数行是偶数,而15是个奇数,所以这一行的数必定是奇数.又数表的每一行的最后一个数就为这一行行数的平方,那么14行的最后一个数为196,那么第15行的第一个数就为197.7. 2004年时,父亲的年龄是哥哥和弟弟年龄之和的4倍;而2010年时,父亲的年龄是哥哥和弟弟年龄之和的2倍,那么父亲出生在______年。
2010陈省身杯数学邀请赛五年级答案
2010年“陈省身杯”国际青少年数学邀请赛五年级1. 计算:58+15⨯⨯8+25⨯8+35⨯8+45⨯8= 。
【分析】: 原式=58358558758958⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯相邻两个加数之间相差258⨯⨯。
是等差数列,所以原式=(58958)521000⨯+⨯⨯⨯÷=2. 在一个减法算式里,被减数、减数与差的和等于2010,而被减数是差的5倍,那么差等于 。
【分析】: 减数+差=被减数,被减数+减数+差=2010,所以2×被减数=2010,被减数=1005,差=被减数÷5=1005÷5=201.3. 数列2,9,17,24,32,39,47,54,62,……的2010项是 。
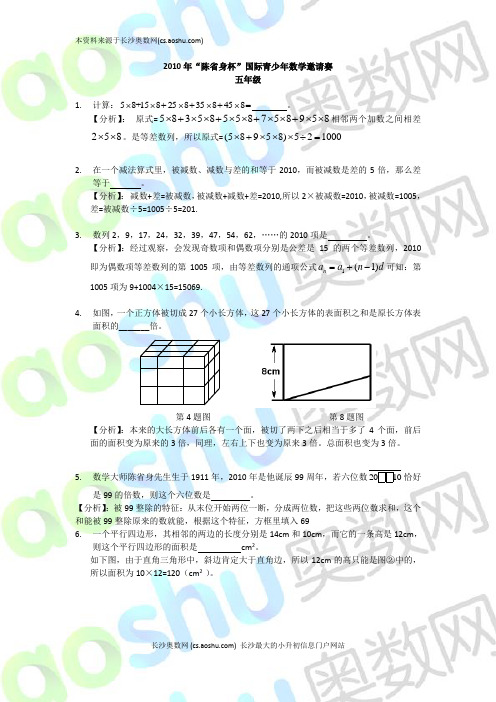
【分析】:经过观察,会发现奇数项和偶数项分别是公差是15的两个等差数列,2010即为偶数项等差数列的第1005项,由等差数列的通项公式1(1)n a a n d =+-可知:第1005项为9+1004×15=15069.4. 如图,一个正方体被切成27个小长方体,这27个小长方体的表面积之和是原长方体表面积的_______倍。
第4题图 第8题图【分析】:本来的大长方体前后各有一个面,被切了两下之后相当于多了4个面,前后面的面积变为原来的3倍,同理,左右上下也变为原来3倍。
总面积也变为3倍。
5. 数学大师陈省身先生生于1911年,2010年是他诞辰99周年,若六位数2010恰好是99的倍数,则这个六位数是 。
【分析】:被99整除的特征:从末位开始两位一断,分成两位数,把这些两位数求和,这个和能被99整除原来的数就能,根据这个特征,方框里填入696. 一个平行四边形,其相邻的两边的长度分别是14cm 和10cm ,而它的一条高是12cm ,则这个平行四边形的面积是 cm 2。
如下图,由于直角三角形中,斜边肯定大于直角边,所以12cm 的高只能是图②中的,所以面积为10×12=120(cm 2 )。
2011年陈省身杯国际青少年数学邀请赛六年级试题及答案

2011年陈省身杯国际青少年数学邀请赛(六年级)试题及答案答题卡(请将答案填入下面的答题卡中)1 2 3 4 56 7 8 9 1011 12 13 14 1516 17 18 19 201.在下面的四个数3.14、3.14%,3.1415和π中,最大的是_________,最小的是_________。
2.一份稿件,甲需要6天才能完成打印,乙需要10天才能完成打印,那么两人合打3天共完成这份稿件的_________。
3.如下图,已知正方形的边长为2cm,则阴影部分的周长为_________cm。
(π取3.14)4.有一个质数,用它分别加上10与4以后,所得和仍为质数,这个质数是_________。
335.如上图表示的长方体(单位:dm ),其长和宽都是3dm ,体积是363dm ,则这个长方体的表面积是_________2dm 。
6.已知A 是大于0的最小自然数,B 是质数中唯一的一个偶数,C 是最小奇质数,C 与D 的和等于70,那么A+B ×C ×D ×(B+C)= _________。
7.一个分数的分子与分母之和是100,将它的分子、分母都减去6后约分得13,那么原来的分数是_________。
8.把同一段铁丝围成一个正方形后,又改围成一个圆形,发现按照面积公式得出的二者面积之和比为4:5,那么在计算圆面积时,圆周率 的取值为_________。
9.一个六位数能被99整除,竖式如图所示,则这个六位数最小可以是_________。
998310.搬运一批货物,甲车单独运要运6次,乙车每次可运72吨,现在甲、乙两车合运,运的次数相同,完成任务时,甲、乙两车搬运货物重量的比是5:3,这批货物共有_________吨。
□□□ □□□ _________□□□ □□□ _________ 011.计算111111111335192124111111111111123234345192021++++++++=⨯⨯⨯⨯⨯⨯⨯⨯ _________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年”陈省身杯”六年级组答案
1.计算:17×47+47×19+19×6+6×34=____________。
答案:2010
方法:原式=47×(17+19)+19×6+6×34=(282+19+34)×6=335×6=2010
2.长方形ABCD 的长为5厘米、宽为3厘米,设其对角线BD 对折后得到的图形如下所示:则图中阴影部分的周长是_______厘米。
答案:16cm
方法:BE=AB, DE=AD
所以阴影部分周长为(5+3)×2=16cm
3. 1911
化成小数后,小数后面的第100位上的数字是_______。
答案:2
方法:1911 1.72∙∙÷=,100÷2=50,所以小数点后第一百个数字为2
4.三个相邻的自然数的乘积是3360,这三个自然数分别是______、______和______。
答案:14,15,16
方法:533602357141516=⨯⨯⨯=⨯⨯
5.用黑白棋子摆成上图(最里面为第1层,奇数层都是黑棋子,偶数层都是白棋子),照这样摆下去,前9层中共有_______粒黑棋子。
答案:220
方法:找规律第一层有12个,每向外一层多8个,所以第三层
有12+16=28,第五层有28+16=44,第七层有44+16=60,第九
层有60+16=76,所以一共12+28+44+60+76=220
6.一个长方形的表面积为88cm 2,若其长宽高之比3:2:1,则其体积为____cm 3。
答案:48立方厘米
88÷2÷(3×2+3×1+2×1)=4平方厘米,所以长方体高为2cm ,宽为4cm ,长为6cm 体积为2×4×6=48立方厘米
7.将7384、4657、89100、2536和5162
分别填入下面空格中,使不等式成立: _____<______<_____<______<______
答案: 254651738936576284100
<<<< 方法:与1进行比较,距离1近的数一定大
8.甲、乙、丙三人共同加工2010个零件,如果他们分别加工一个零件需要10分钟、12分钟和25分钟,那么当工作完成时,甲比丙多加工了_____个零件。
答案:540
方法:甲乙丙三人
9.一个两位数的十位数字是个位数字的3倍。
如果把这个两位数减少36,所得到的数等于原数的十位数字和个位数字对调后的数,原数是______。
答案:62
方法:设个位数字为x ,十位数字为3x ,那么这个两位数为31x ,对调之后的两位数为13x (使用位置原则),可以列出方程31x-36=13x ,解出x=2,所以原数为62
10. 东西两地相距9千米,小明从东向西走,每分钟走60米,小莉从西向东走,小辉骑车从东向西走,每分钟300米,三人同时动身,途中小辉遇见小莉即折回向东骑,遇见小明又折回向西骑,再遇见小莉又折回向东骑,...这样往返,如果小辉第二次返回遇见小明时,小明与小莉相距恰好1千米,那么小莉每分钟走( )米。
答案:100
方法:列方程90009000(60)90006000300300
36060
x x x x -+++=++设速度每分钟走x 米,90009000(60)9000600030030036060x x x x -+++=++ 求出x=100
11.已知A=(1+2+...+2009)×(2+3+ (2010)
B=(1+2+...+2009+2010)×(2+3+ (2009)
则在A 和B 中,较大的数是______。
答案:A
方法:换元设1+2+…+2009=a ;2+3+…+2009=b
原式A=a ×(b+2010)B=(a+2010)×b
展开之后发现A 比较大
12.参加“2010陈省身数学周”活动的学生共有1200人,其中女生人数的
38比男生人数的27多了80人,则参加此次比赛的女生共有_____人。
答案:640
方法:设原有女生x 人,则男生有(1200-x )人 可以列出方程32(1200)8087
x x --=,x=640 13.下图是由五个圆所构成的,其中总公共有3种不同长度的直径,且有部分的圆彼此相切,如图所示,若最大圆内白色的面积是20cm 2,则其中阴影部分的面积是______cm 2。
答案:10
方法:设最小圆的半径为x ,则其他两种圆的半径为2x ,3x ,
空白部分面积为2222946x x x x ππππ-+=
阴影部分面积为22243x x x πππ-=
所以阴影面积是空白部分的一半
14.在方框中填入恰当的数字使乘法竖式成立,则算式成立时,其中两个乘数之和为_____。
答案:453
方法:略两个乘数分别为157和296
15.把一根圆木棍分成等长的4节,每节用红、黄、蓝三中颜色的一种来涂,且三中颜色都要用上,共有_____种不同的涂法。
(如果两根木棍可以经过翻转使得颜色顺序相同,那么认识者两根是一种涂法)
答案:18
方法:乘法原理:3×3×2×1=18
16.计算:
2010201020092010200920082010200943________.2008200820072008200720062008200721
⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯+++⋅⋅⋅+=⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯ 答案:4036080
方法:提取2010和2009,原式=2010×2009×(1-12009
)=4036080
17.李大爷出生在上个世纪,他今年(2010年)的年龄恰好是他出生那一年年份各位数数字之和的4倍,则李大爷今年的年龄是________岁,他出生在________。
答案:1950 60 方法:设李大爷出生年份为19ab ,所以李大爷今年的年龄为(10)(10)a b --,所以又10(10-a )+(10-b )=4(1+9+a+b ),化简得14a+5b=70,解不定方程得a=5,b=0,所以今年
60岁
18.经理有四封信先后交给打字员,要求打字员总是先打最近接到的信。
比如,正在打第3封信时第4封信到了,应立即停下第3封信,转打第4封信;第4封打完后,接着打第三封,而不能先打第1或第2封信,打字员打完这四封信的先后顺序有____种可能。
答案:14种
方法:枚举法
1234,1243,1324,1342,1432,2134,2143,2314,2341,2431,3214,3241,3421,4321
19.某水池有甲乙两个排水管和一个进水管,如果盛满一池水,单开甲管或乙管分别需要6小时和4小时才能把水排完。
如果现在水池中有一部分水,并且当同时打开甲管和进水管,用了10小时就将水排完;而如果同时打开甲管、乙管和进水管,则只用2.5小时就将水排完,那么水池中的水占全部水池的____分之______。
答案:六分之五
方法:甲工效为六分之一,乙工效为四分之一,设进水管工效为x 列出方程:
11110() 2.5(-x)664x -=+ x=112
所以10×(1/6-1/12)=5/6
20.某班参加一次智力竞赛,共abc 三题,每题或者满分或者0分,其中题a 满分20分,题b 、题c 满分分别为25分;竞赛结果,每个学生至少答对了一题,三道题全对的有1人,答对其中2道题的有15人,答对题a 的人数与答对题b 的人数之和为29人;答对题a 的人数与答对题c 的人数之和为25人;答对题b 的人数与答对题c 的人数之和为20人;则这个班的平均成绩是______分。
答案:42
方法:答对题a ,b ,c 的人数总和为(29+25+20)÷2=37人,所以答对a ,b ,c 得人数分别为17,12,8人,所以总分为20×17+25×12+25×8=840人,总人数为17+12+8-15-1×2=20人,所以平均分为42分。
