附合导线平差范例
导线测量平差实例

导线测量平差实例第一篇:导线测量平差实例导线测量平差实例闭合导线:名称表示原理(导线长)D实测边长总合(角度总和)∑β实测左角相加的总和(角度闭合差)Fβ实测左角相加的总和的秒位数(坐标闭和差)Fx△x计算出的坐标增量之合Fy△y计算出的坐标增量之合(距离闭合差)FFx平方加Fy平方开根号(导线精度)KF/D(1÷F×D)附合导线:名称表示原理(导线长)D实测边长总合(角度总和)∑β实测左角相加的总和(角度闭合差)Fβ实测推算出的终点方位角减理论的终点方位角(坐标闭和差)Fx△x总合减(终点x坐标减起始x坐标)Fy△y总合减(终点y坐标减起始y坐标)(距离闭合差)FFx平方+Fy平方开根号(导线精度)KF/D(1÷F×D)坐标增量计算:△x12=D12×cosa12△y12=D12×sina12D :实测两点间的距离。
a :实测两点间的方位角。
近似平差方法:①将角度闭合差除以测站数:Fβ÷N(N表示测站数)=∩(角度均值),然后将角度均值加到实测右角中。
②将Fx平方加Fy平方开根号,得出距离闭合差,用距离闭合差除以观测边长数得出距离均值,然后将距离均值加到每一条实测边长中。
③从起测点开始,再通过公式△x12=D12×cosa12、△y12=D12×sina12求出坐标增量。
用上一测站的坐标加上坐标增量就得出平差后的坐标第二篇:附和导线平差程序[QBASIC]附和导线平差程序[QBASIC]由本人在网络上收集整理DECLARE FUNCTION DEG!(X!)DECLARE FUNCTION DMS!(XX!)DECLARE FUNCTION XCHAR$(XX!, N!)CLSPRINTPRINT “ 附和导线平差程序(2.0R)”PRINT “ 作者:徐振刚”PRINT “ 1999年12月31日”PRINT “功能:本程序可以用来进行一般导线平差计算,包括附和导线、闭合导线和支导线,其中” PRINT “ 闭合导线和支导线需对原始数据进行一定处理。
导线测量平差实例

导线测量平差实例
闭合导线:
名称表示原理
(导线长) D 实测边长总合
(角度总和)∑β 实测左角相加的总和
(角度闭合差)Fβ 实测左角相加的总和的秒位数
(坐标闭和差)Fx △x计算出的坐标增量之合
Fy △y计算出的坐标增量之合
(距离闭合差) F Fx平方加Fy平方开根号
(导线精度)K F/D(1÷F×D)
附合导线:
名称表示原理
(导线长) D 实测边长总合
(角度总和)∑β 实测左角相加的总和
(角度闭合差)Fβ 实测推算出的终点方位角减理论的终点方位角
(坐标闭和差)Fx △x总合减(终点x坐标减起始x坐标)
Fy △y总合减(终点y坐标减起始y坐标)
(距离闭合差) F Fx平方+Fy平方开根号
(导线精度)K F/D(1÷F×D)
坐标增量计算:
△x12=D12×cosa12
△y12=D12×sina12
D :实测两点间的距离。
a :实测两点间的方位角。
近似平差方法:①将角度闭合差除以测站数:Fβ÷N(N表示测站数)=∩(角度均值),然后将角度均值加到实测右角中。
②将Fx平方加Fy平方开根号,得出距离闭合差,用距离闭合差除以观测边长数得出距离均值,然后将距离均值加到每一条实测边长中。
③从起测点开始,再通过公式△x12=D12×cosa12 、△y12=D12×sina12求出坐标增量。
用上一测站的坐标加上坐标增量就得出平差后的坐标。
附合导线平差自动计算表 修改版
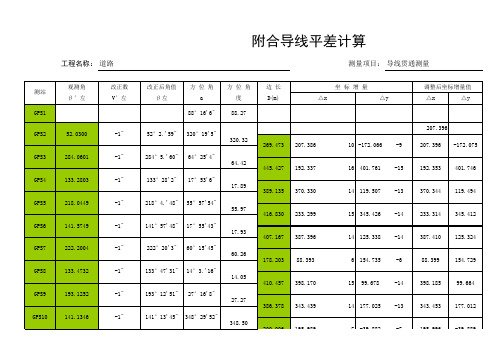
改正后角值 β左
方位角 a
方位角 度
231°18'35" 39°48'27"
39.81
157°2.'7" 16°50'34"
16.84
216°29'20" 53°19'53"
53.33
118°21'27" 351°41'20" 351.69
300°37'38" 112°18'59" 112.32
81°59'6" 14°18'4"
259°5.'55" 50°54'53"
50.91
边长 D(m) 412.681 219.463 103.147 309.760 144.002 165.164 101.439 149.565
坐标增量
△x 178.378
△y 15 372.138 -14
215.958
8 -39.063 -8
51.296
221.992 216.035
143.775
-8.182
163.098
26.076
22.792
98.843
131.837 -70.645
GPS29
4822°39'9"
-22"
角度闭合差改正计算:
∑β测-n*180= 37°20'51"
4822°38'47" 坐标增量闭合差计算: ∑△x=
7,273.778 5098.228 5098.228
25
1001411.681 337826.757
拓普康全站仪导线测量与平差示例

TOPCON 北京技术中心 86-10-67802799
6、在主菜单选择[测量],点击[BS/FS测量]开始测量。
显示的对话框如下:
TOPCON 北京技术中心 86-10-67802799
7、确认后视点点号(b),在盘左状态下照准该后视点
按下面板上的[ENT]键观测并记录数据。
TOPCON 北京技术中心 86-10-67802799
TOPCON 北京技术中心 86-10-67802799
TOPCON 北京技术中心 86-10-67802799
其中限差设置部分,
Hz表示水平角限差:[盘左-(盘右-180)] VA表示垂直角限差:[盘左+盘右-360]
D表示距离限差:[盘左-盘右]
测量方法中“盘左-〉盘右”表示的观测顺序为: 盘左 BS -〉盘左 FS,盘右 FS-〉盘右 BS 注:以上限差应该根据所测导线的等级,按对应的规范 要求来设置。
按下[ENT]键测量,如果限差超限,会显示如下对话框:
点击[重测],重新照准,再次按[ENT]进行测量;点击[采用]则保留 当前测量值。
TOPCON 北京技术中心 86-10-67802799
10、盘右观测后视点(b)
盘右观测完前视点后,TopSURV自动切换到后视点盘右观 测界面:
按[ENT] 观测并记录数据(如果超限也会有提示窗口出现)。
TOPCON 北京技术中心 86-10-67802799
5、点击[坐标平差],显示坐标改正结果
点击[保存报表],可以将此次平差的相关数据 保存到文件中。
TOPCON 北京技术中心 86-10-67802799
6、以下是一个闭合导线的示例(在TopSURV中仍称为 附合导线,并按附合导线进行平差处理)
1-11单导线条件平差计算--附合导线坐标条件方程

平差值条件方程: ALˆ A0 0
改正数条件方程: AV W 0
STEP1
表达成角度和边
长平差值的形式
STEP2
表达成角度和边
长改正数的形式
附合导线坐标条件方程
1、纵坐标附合条件方程式
xˆN 1 xC 0
STEP1
xˆN 1 xB [xˆi ]1N
xˆi Sˆi cosTˆi
3
N
SN-1
SN
D
TCD
βN+1
C (N+1)
纵坐标符合条件方程式就是:xˆN 1 xC 0 横坐标符合条件方程式就是:yˆ N 1 yC 0
B点坐标的已知值 (xB , yB ) 或 (x1, y1)
C点坐标已知值
(xC , yC ) 或 (xN 1, yN 1)
C点坐标观测值
A
D
β2
β4
βN
2
4
β1 S1 S2 β3 S3
N
SN-1
SN βN+1
3
B(1)
附合导线示例图
C(N+1)
附合导线坐标条件方程
补充:具体计算时的单位选取
如果x、y 以米为单位,w、vS 以厘米为单位、vβ 以秒为单位。
[cos Ti
vSi
]1N
1
[( yN 1
yi )vi
]1N
STEP2
表达成角度和边 长改正数的形式
xˆN 1 xB [xˆi ]1N
xˆi Sˆi cosTˆi
非线性从这个式子着手!!
Tˆi TAB ˆ j
i
180
符合导线近似平差

附合导线近似平差附合导线近似平差L1C=0:A>9ÞDefm 2(A-9△Lbl l:C=C+1:{I}:Prog 3:A[C+8]=D:C≠AÞGoto 1△{B}:Prog B:B=D-B:D=B/A:Prog C▲C=0L2Lbl 2:C=C+1:A[C+8]=A[C+8]-DC:B=A[C+8:Prog C▲C≠AÞGoto 2△C=8:D=0:E=0:F=0L3Lbl 3:C=C+1:{B}:D=D+B:E=E+Bcos A[C:F=F+Bsin A[C:A[A+C] =B:C≠A +7ÞGoto 3△D▲{BI}:BGHI:E=E+B-H▲F=F+G-I▲D/√(E2+F2▲E=E/D:F=F /DL4C=8:Lbl 4:C=C+1:B=A[A+C]cos A[C]+B-EA[A+C▲G=A[A+C] sin A[C]+G-FA[A+C▲C≠A+7ÞGoto4△Defm 0说明:①程序10用以单一附合导线的近似平差计算;②程序中:A=测站数、B=起算边坐标方位角、附合边坐标方位角、导线边边长、起点纵坐标、I=观测角(左角)、终点横坐标、G=起点横坐标、H=终点纵坐标;③程序设计可以计算9个测站,大于是9站时只要计算器剩余有步骤数,程序会自动扩充储存器增加储存变量;④算例如表:按Prog 10调用程序显示A?输入测站数5,按EXE键、显示B?输入起算边的坐标方位角169.5359,按EXE键、显示I?输入B点的观测角93.3642,按EXE键、显示I?输入C点的观测角179.56,依次输入各观测角…,按EXE键、显示B?输入附合边的坐标方位角250.06,按EXE 键、显示导线的角度闭合差-0.003699999(-37″),按EXE键、显示平差后B点至C点的坐标方位角83.30484,按EXE键依次显示各导线边平差后的坐标方位角…,按EXE键、显示B?输入B点至C点的边长126.11,按EXE键、显示B?依次输入各导线边的边长…,按EXE键、显示各边长之和508.96,按EXE键、显示B?输入起点纵坐标801.53,按EXE键、显示G?输入起点横坐标724.84,按EXE键、显示H?输入终点纵坐标959.29,按EXE键、显示I?输入终点横坐标1158.41,按EXE 键、显示纵坐标闭合差0.093449934,按EXE键、显示横坐标闭合差-0.02045631,按EXE键、显示导线全长相对闭合差5320.360577(K=1/5320),按EXE键、显示C点纵坐标815.754,按EXE 键、显示C点横坐标850. 148,按EXE键依次显示D、E、F、G点的纵横坐标。
1-10单导线条件平差计算--附合导线方位角条件方程-修改

坐标方位角条件就是: TˆN 1 TCD 0
TˆN 1 TCD 0
代入
TˆN 1
TAB
[ˆi
]N 1
1
(N
1) 180
? 思考
TCD TN 1 TˆN1
TAB [ˆi ]1N 1 (N 1) 180 TCD 0 代入 ˆi i vi (i 1,2,, N 1)
[vi ]1N 1 wT 0
wT (TAB [i ]1N 1 (N 1) 180 TCD ) (TN 1 TCD )
A
D
β2
β4
βN
坐标方位角改正数条件方程: [vi ]1N 1 wT 0
β1 B(1)
2
4
S1 S2 β3 S3
3
N
SN-1
( xˆ N 1,yˆ N 1 )
条件方程类型:
1坐标方位角附合条件方程式 2纵坐标附合条件方程式 3横坐标附合条件方程式
A
D
β2
β4
βN
β1 B(1)
2
4
S1 S2 β3 S3
3
N
SN-1
SN βN+1
C(N+1)
附合导线示例图
理论
感谢聆听,批评指导
公式
思考
平差
算例
Xi’an University of Science & Technology
举一 反三
治学 严谨
Error Theory and Surveying Adjustment
逻辑
性强
主讲人:史经俭 张静 席晶
本讲内容
附合导线方位角条件方程
附合导线严密平差算法总结

附合导线严密平差算法总结图1如图的单一附合导线,有4个已知点A、B、C、D,2个未知点TP1、TP2。
设观测边数为n, 则未知点数为n-1, 观测角数为n+1。
以上图为例,n = 3。
观测边为:S1 = B->TP1,S2 = TP1->TP2, S3 = TP2->C思路:由于A、B坐标已知,则可以算出起始方位角,再根据B点坐标和每个观测角(夹角,左角)推算出TP1、TP2、C点的近似坐标值。
如果是用全站仪进行测量,则用盘左盘右重复观测求平均的方式,直接测出TP1、TP2、C点的近似坐标值以及CD的方位角。
再根据c点的已知坐标与近似坐标求坐标闭合差,由CD的已知方位角和近似方位角求角度闭合差,两个闭合差联立求得边长和角度的改正数,最后求得未知点的坐标平差值。
条件平差过程:1.建立条件方程,求得条件系数2.求法方程系数3.求权阵4.计算出联系数K5.解算出观测值改正数V6.由观测值和改正数计算平差值详细步骤如下:1、建立条件方程在单一附合导线中,只需要三个条件方程即:方位角附合条件、纵坐标附合条件和横坐标附合条件方程。
(省略了条件方程的推导过程,详细过程请查看参考资料:《测量平差.pps》)(1)方位角附合条件[Vβi]n+11+ Wβ= 0式中,Wβ= - (T0– T CD+ [βi]n+11 - (n+1)*180°)(角度闭合差)βi ——角度观测值(夹角,左角)Vβi ——各观测角的改正数。
如果是用全站仪观测,则Wβ= - (T CD– T CD)式中,T CD ——CD的方位角观测值,T CD ——CD的已知方位角(2)纵坐标X附合条件方程[Cos TI * VSi]1n - (1/ ρ”)* [(Yn+1- Yi) * Vβi]1n - W x = 0;式中,TI——各方位角观测值(近似值)VSi——边长改正数Yn+1—— C点即终止点的横坐标Y的观测值(近似值)Yi——待定点的横坐标Y的观测值Wx = - (Xn+1- XC)XC—— C点即终止点的纵坐标X的已知值ρ” = 2062.65(3)横坐标Y附合条件方程[Sin TI * VSi]1n + (1/ ρ”)* [(Xn+1- Xi) * Vβi]1n– W Y = 0;式中,TI——各方位角观测值(近似值)VSi——边长改正数Xn+1—— C点即终止点的纵坐标X的观测值(近似值)Xi——待定点的纵坐标X的观测值WX = - (Yn+1- YC)YC—— C点即终止点的横坐标Y的已知值ρ” = 2062.652、求条件方程的系数矩阵联立3个方程得改正数条件方程组:[Vβi]n+11+ Wβ= 0[Cos TI * VSi]1n - 1/ ρ”* [(Yn+1- Yi) * Vβi]1n - W x = 0;[Sin TI * VSi]1n + 1/ ρ”* [(Xn+1- Xi) * Vβi]1n– W Y = 0;其系数矩阵arrA为:(即改正数V的系数,此处以图1为例, n = 3)3、联系数法方程(简称法方程)AP-1A T K – W = 0A——系数矩阵arrAK ——乘系数P ——权阵W ——闭合差矩阵由上得法方程的系数阵N:N = AP-1A T(权的推导见参考资料:《全站仪观测导线测量平差方法的研究.pdf》)角度权:P βi = 1;(因为角度的标称精度是固定的,各观测角权值相等) 边长权:P Si = (μ0 *μ0 ) / (M D * M D )(误差比例系数固定,边长的误差与距离有关,因此不一致)式中,μ0 ——先验测角中误差,以秒为单位 M D —— 距离观测中误差若 导线边长为S i (米),e1 为仪器的边长标称固定误差(mm ),e2为仪器的边长比例误差系数(无单位),则M D = ± (e1 + e2 * S i * 0.001)mm 需转化为厘米:M D = M D ** 0.1 (cm )由于此处是要P 的逆矩阵P -1,因此要求P 的各元素的倒数(P 是对角矩阵,对角矩阵的逆矩阵就是原矩阵元素的倒数) Psi = 1/ Psi ;由上可得,P -1 矩阵如下:4、求改正数由于N 已经在前面的步骤中求出,求N 的逆矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
观测角度形式角度改正数改正后角度
方位角度形式边长D
°′″°″°°′″°
m A D
∑
109650
24
1096.84
665.38
相对中误差=
F D ∶∑S =1∶2188.22
说明:
1、表中红色数据为观测值;蓝色数据为已知值;绿色数据为角度、方位角以度(不以度分秒)的表达形式,会自动计
2、C19和D19处的数字不能为负或大于60,K列数字不能为负或大于360,否则需人工处理。
测量:记录:
计算:
审核:
4C 2784312212
52
30B 1292175156方位角α
180.7322
230.3706206.8761202.3833
203.11563
1804354角度观测值(左角)点号
317
52
63024306
3018180.731667222292.5016667156.505
175.506667精度分析
附合导线平差计算程序
278.72212.87522
278.7206
212.8756
175.5072
92.50222
156.5056
334
42
42317.8683133.84
154.71
80.74
148.93
301.8361334.7117
147.16
Δx
Δy
υx
υy
Δx′
Δy′
x
y
-357.369-387.255-0.13071-0.27455
秒)的表达形式,会自动计算,可隐藏;紫色数据为平差结果。
-137.00277.59672日期:
-125.021-0.02926-0.02891-58.5294
-125.082
-0.06145-0.060723802.851
4006.77
-70.0025
3903.633
3805.1083833.631
3943.138-103.137
-30.7792
4028.533730.436坐标增量计算值(m)坐标增量改正数(m)改正后的坐标增量(m)
坐标(m)
-0.05522-0.06384-0.03331-0.02629-0.03039-85.3658程序
-0.01586-85.3921-138.03-74.6727-103.082-69.9386-30.7459-137.999-74.6568-136.9733671.033619.24
3593.4333744.322
77.62563-58.468。
