高一数学课件 二次函数在闭区间上的最值
二次方程根的分布情况以及二次函数在闭区间上的最值归纳(完整版)
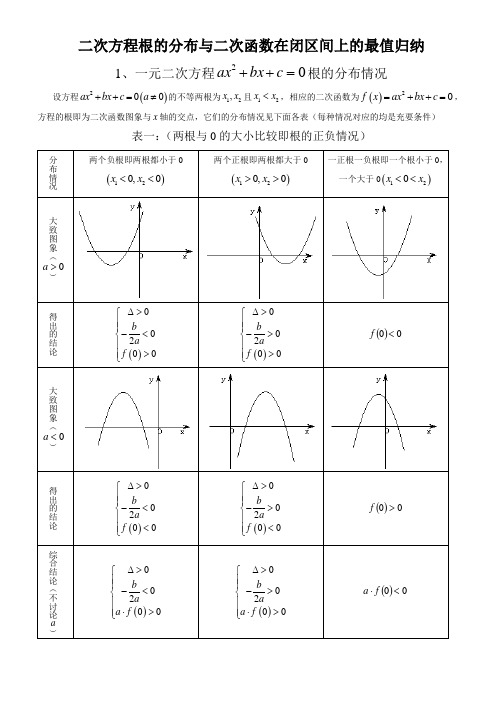
二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)k k k根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求; 2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
二次函数在闭区间上的最值精品文档8页

二次函数在闭区间上的最值一、知识要点:一元二次函数的区间最值问题,核心是函数对称轴与给定区间的相对位置关系的讨论。
一般分为:对称轴在区间的左边,中间,右边三种情况.设,求在上的最大值与最小值。
分析:将配方,得顶点为、对称轴为当时,它的图象是开口向上的抛物线,数形结合可得在[m,n]上的最值:(1)当时,的最小值是的最大值是中的较大者。
(2)当时若,由在上是增函数则的最小值是,最大值是若,由在上是减函数则的最大值是,最小值是当时,可类比得结论。
二、例题分析归类:(一)、正向型是指已知二次函数和定义域区间,求其最值。
对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。
此类问题包括以下四种情形:(1)轴定,区间定;(2)轴定,区间变;(3)轴变,区间定;(4)轴变,区间变。
1. 轴定区间定二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”。
例1.函数在区间[0,3]上的最大值是_________,最小值是_______。
解:函数是定义在区间[0,3]上的二次函数,其对称轴方程是,顶点坐标为(2,2),且其图象开口向下,显然其顶点横坐标在[0,3]上,如图1所示。
函数的最大值为,最小值为。
图1练习. 已知,求函数的最值。
解:由已知,可得,即函数是定义在区间上的二次函数。
将二次函数配方得,其对称轴方程,顶点坐标,且图象开口向上。
显然其顶点横坐标不在区间内,如图2所示。
函数的最小值为,最大值为。
图22、轴定区间变二次函数是确定的,但它的定义域区间是随参数而变化的,我们称这种情况是“定函数在动区间上的最值”。
例2. 如果函数定义在区间上,求的最小值。
解:函数,其对称轴方程为,顶点坐标为(1,1),图象开口向上。
如图1所示,若顶点横坐标在区间左侧时,有,此时,当时,函数取得最小值。
图1如图2所示,若顶点横坐标在区间上时,有,即。
当时,函数取得最小值。
图2如图3所示,若顶点横坐标在区间右侧时,有,即。
二次函数在闭区间上的最值问题

第三讲 二次函数在闭区间上的最值问题 一.知识点介绍1.区间的概念设a 、b 是两个实数,且a<b ,规定:说明:① 对于[a,b],(a,b),[a,b),(a,b]都称数a 和数b 为区间的端点,其中a 为左端点,b 为右端点,称b-a 为区间长度;②在数轴上,这些区间都可以用一条以a 和b 为端点的线段来表示,在图中,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点;③实数集R 也可以用区间表示为(-∞,+∞),“∞”读作“无穷大”,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”,还可以把满足x ≥a, x>a, x ≤b, x<b 的实数x 的全体分别表示为[a,+∞)、(a,+∞)、(-∞,b]、(-∞,b)。
我们把以上区间记为A ,若x 是A 中的一个数,就说x 属于A ,记作x ∈A 。
否则就说x 不属于A ,记作x ∉A 。
2. 二次函数f(x)=ax 2+bx+c(a≠0)在x ∈[α,β]上的最值: 当a>0时,有三种情况:从上述a>0的三种情况可得结论:(1)若[,]2baαβ-∈,则当2b x a =-时,2min4()24b ac b y f a a-=-=,它的最大值为()f α与()f β中较大的一个。
(2) 若[,]2baαβ-∉,则最大值为()f α与()f β中较大的一个,另一个即为最小值。
当a<0可作同样处理。
二.例题讲解:类型一“轴定区间定”例1:已知f(x)=x 2-x+2,当x 在以下区间内取值时,求f(x)的最大值与最小值。
(1) x ∈[-1,0] (2) x ∈[0,1] (3) x ∈[1,2]变式1:求y =的最值。
变式2:已知0≤x≤1,求y =的最值。
变式3:求函数y x =+的最小值。
类型二“轴变区间定”例2:求函数f(x)=2x 2-2ax+3在区间[-1,1]上的最小值。
二次函数在闭区间上的最值问题

二次函数在闭区间上的最值问题
最值问题是函数的基本概念之一,它旨在求出函数在定义域中的最大值和最小值。
函数的最值问题也是极其重要的问题,其研究可以帮助我们求出目标函数的最优解,从而获得最佳的求解结果。
在闭区间上的二次函数最值问题中,其对应的函数形式为:
$f(x)=ax^2+bx+c$
其中,a,b,c为常量。
问题要求给定区间[a,b],求出f(x)在这个区间内的最大值和最小值。
一、求二次函数在闭区间上的最值
二、最值求解:
最终,我们就可以得出该函数在指定的闭区间上的最大值和最小值。
高中数学二次函数在闭区间上的最值优秀课件

物联网工程 光电信息科学与工程
通信工程 医学信息工程 电气工程及其自动化
科类 理工类
理工类 理工类
理工类 理工类 理工类 理工类 理工类
学制 四年
四年 四年
四年 四年 四年 四年 四年
国家“985工程〞 、“211工程〞重 点建设高之一
20xx年9月,入选国家“双 一流〞〔世界一流大学和 一流学科〕A类建设高。
在数据分析、软件开发、保险金融、通讯工程、航空航 天、建筑设计、公司企划等都离不开函数的相关知识。
练习题
1.已 知 f(x)x22x2的 定 义 域 和 值 域 都 为 [1,b],则 b的 值 为 _____.
2.关于已知x的方程 sin2x-2sinx-a=0有实数解,
则a的取值范围是
3.若不等式 2xx2 a 对于任意的x∈[-2,3]恒
清水河、沙河、九里堤三个区, 占地4100余亩,20xx年10月截 止,设23个学院部、66个本科专 业;13个博士后流动站,16个一 级学科博士学位授权点、1个博 士专业学位授授权点,27个一级 学科硕士学位授权点、8个专硕 士业学位授权点;教职工3800余 人;全日制在生33000余人,其 中博士、硕士研究生12000余人
专题复习:二次函数在闭区间上的最值问题
xx三十 范绍超 20xx年11月
复习旧知,进入新课:二次函数的相关知识
典型例题:函数f(x)= x2–2x –3.假设x∈[ –2,0 ] 求函数f(x)的最值。
f(x)ma xf(2)5 f(x)mi nf(0)-3
y
y
O
–2
3
x
O2
–2
3
x
X=1
二次函数在闭区间上的最值问题及其应用

0 一≤, 0 n 2j ()la = , ≤ l ≤ ≤ 日 gc= 等~ 詈 即 , 厂 1 ( / -
+
f 1 =“+b+1 , ) :0
【 ( =2 + 6= 1 f a) “ .
号= 等+ ;当 1 时g ) 一 号④ 号 , 2 ,n 即“ (
> 一2 舍去 ) (
例 1 已 函数
.
厂 ) 一 + ( = 号。
L() f或 4 舍去 ) :
g ) ( 求 函 数 f( 彳 ( ; n) ) F区间 0 l 的最大 值 , 上
区 『左 边 、 间 内 、 问有 边 三种 情 况 论 ; 口 J 区 最 值 按 对称 轴 在 区 间 中 点 左 边 、 区 『 中点 右 边 两 种 和 日 J
一
、
构 建 轻松 愉 快 的 英 语 学 习环 境 应 注 意 的 问
题 区 间 端 点 和 中 点 要 同 时考 虑 , 个 点 把 实 数 集 二
1募 : 若 独 虑 大 和小 , 要 ] 本 罂 套 最值 最嚣前 上析 题单考 分 易 值者
本 个零点把实数集分成三部分, 因此分三种博况讨 、 。
解: 数_ ) X+x b 称轴为 函 厂 : 2 a+ 对 ( =一 号,
薯 鼻 ! 篝 銮 } 差至 蠡 零 i
含 参二次函数在区间 上最值问题是 备级考蒜
高簧 葜 莲 咎 运 爵 覆
若能恰 当地舍弃细节 , 整体分析 , 口使解题变得衙 则 ]
鬻 瞳 辩
・ u
■ 杜艳 丽
教2 材 探 9 析
营造轻松和谐的环境 走出英语学习的国境
( 圳
(  ̄J. a< )
。
综
二次函数闭区间上的最值问题

二次函数闭区间上的最值问题与根的分布一、二次函数闭区间上的最值问题一元二次函数的区间最值问题,核心是对函数对称轴与给定区间的相对位置关系的讨论。
一般分为:对称轴在区间的左边,中间,右边三种情况.设2()(0)f x a x b x c a =++≠,求f x ()在[]x m n ∈,上的最大值与最小值。
分析:将f x ()配方,得对称轴方程x b a=-2当a >0时,抛物线开口向上 若-∈b am n 2[],必在顶点取得最小值,离对称轴较远端点处取得最大值; 若-∉b am n 2[], 当a >0时,抛物线开口向上,此时函数在[]m n ,上具有单调性,故在离对称轴x b a=-2较远端点处取得最大值,较近端点处取得最小值。
当a <0时,如上,作图可得结论,对二次函数的区间最值结合函数图象总结如下: 当a >0时m a x121()()()22()1()()()22b f m m n a f x b f n m n a ⎧-≥+⎪⎪=⎨⎪-<+⎪⎩如图如图,,f x f n b a n f b a m b a n f m b a m ()()()()()()()m in=->-≤-≤-<⎧⎨⎪⎪⎪⎩⎪⎪⎪,,,如图如图如图2222345当a <0时f x f n b a n f b a m b a n f m b a m ()()()()()()()m ax=->-≤-≤-<⎧⎨⎪⎪⎪⎩⎪⎪⎪,,,如图如图如图2222678m i n 9101()()()22()1()()()22b f m m n a f x b f n m n a ⎧-≥+⎪⎪=⎨⎪-<+⎪⎩如图如图,,1. 定二次函数在定区间上的最值二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”。
例1. 函数y x x =-+-242在区间[]03,上的最大值是_________,最小值是_______。
二次函数在闭区间上的最值课件

区间内取得最值
总结词
当二次函数的对称轴恰好落在区间内时,函数在对称轴上取得最值。
详细描述
对于一般的二次函数$f(x) = ax^2 + bx + c$,其对称轴的方程是$x = -frac{b}{2a}$。当这个对称轴落在区间内 时,函数在这一点上取得最值。具体来说,如果二次函数的开口向上,那么在对称轴上取得最小值;如果二次函 数的开口向下,那么在对称轴上取得最大值。
区间端点处取得最值
总结词
对于开口向上的二次函数,其在区间端点处取得最小值;对于开口向下的二次 函数,其在区间端点处取得最大值。
详细描述
由于二次函数的开口方向决定了函数的增减性,因此对于开口向上的二次函数, 其在区间端点处取得最小值。对于开口向下的二次函数,由于其在整个区间内 是递减的,所以在区间端点处取得最大值。
实际应用拓展
将二次函数在闭区间上最值的研究成果应用于更多实际问题中,提 高解决实际问题的能力。
数学与其他学科的交叉研究
探索二次函数在闭区间上最值与其他数学分支或学科的交叉研究, 促进数学的发展和应用。
THANK YOU
二次函数在区上的最 件
• 二次函数的基本性质 • 二次函数在开区间上的最值 • 二次函数在闭区间上的最值求法 • 二次函数在闭区间上的最值应用 • 总结与展望
二次函数的定义和表达式
总结词
二次函数是形式为 $f(x) = ax^2 + bx + c$的函数,其中 $a neq 0$。
详细描述
二次函数的一般形式是 $f(x) = ax^2 + bx + c$ ,其中 $a$ 、 $b$和$c$是常数,且$a neq 0$。
01
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)若x∈[–2,0],求函数f(x)的最值;
(2)若x∈[ 2,4],求函数f(x)的最值;
(3)若x∈[ 1 , 5 ],求函数f(x)的最值;
22
y
(4)若x∈[ 1 , 3],求
22
函数f(x)的最值;
(5)若 x∈[t,t+2]时, 求函数f(x)的最值.
t
t +2
–1 0 1 2 3 4 x
y
–1 0
1
2
x
例3、已知函数f(x)=x2+ax+b,x∈[0,1], 试确定a、b,使f(x)的值域是[0,1].
y
–1 0
1
2
x
例3、已知函数f(x)=x2+ax+b,x∈[0,1], 试确定a、b,使f(x)的值域是[0,1].
y
–1 0
1
2
x
例3、已知函数f(x)=x2+ax+b,x∈[0,1], 试确定a、b,使f(x)的值域是[0,1].
(5)若x∈[t,t+2]时,
求函数f(x)的最值.
t
t +2
–1 0 1 2 3 4 x
例1、已知函数f(x)= x2 –2x – 3.
(1)若x∈[–2,0],求函数f(x)的最值;
(2)若x∈[ 2,4],求函数f(x)的最值;
(3)若x∈[ 1 , 5 ],求函数f(x)的最值;
22
y
13
y
–1 0 1 2 3 4 x
例1、已知函数f(x)= x2 –2x – 3.
(1)若x∈[ –2,0],求函数f(x)的最值; (2)若x∈[ 2,4],求函数f(x)的最值;
(3)若x∈[ 1 , 5 ],求
y
22
函数f(x)的最值;
1
5
2
2
–1 0 1 2 3 4 x
例1、已知函数f(x)= x2 –2x – 3
高中数学
二次函数在闭区间上的最值
石家庄市42中学 于祝
例1、已知函数f(x)= x2–2x –3. (1)若x∈[ –2,0 ], 求函数f(x)的最值;
y
–2 0 1
3
x
例1、已知函数f(x)= x2 –2x – 3. (1)若x∈[ –2,0 ],求函数f(x)的最值; (2)若x∈[ 2,4 ],求函数f(x)的最值;
[–1,2]上的最值.
y
y
–1 0 1 2
x
–1 0 1 2
x
评注:例2属于“轴变区间定”的问题,看作 对称轴沿x轴移动的过程中,函数最值的变化, 即对称轴在定区间的左、右两侧及对称轴在定 区间上变化情况,要注意开口方向及端点情况。
y
y
–1 0 1 2
x
–1 0 1 2
x
例3、已知函数f(x)=x2+ax+b,x∈[0,1], 试确定a、b,使f(x)的值域是[0,1].
(4)若x∈[ , ],求
22
函数f(x)的最值;
(5)若x∈[t,t+2]时,
求函数f(x)的最值.
t
t +2
–1 0 1 2 3 4 x
例1、已知函数f(x)= x2 –2x – 3.
(1)若x∈[–2,0],求函数f(x)的最值;
(2)若x∈[ 2,4],求函数f(x)的最值;
(3)若x∈[ 1 , 5 ],求函数f(x)的最值;
(3)当x0 [m,n]时,f(m)、f(n)中的较大
者是最大值,较小者是最小值.
[–1,2]上的最值.
y
–1 0 1 2
x
例2、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
y
–1 0 1 2
x
例2、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
y
y
–1 0 1 2
x
–1 0 1 2
x
例2、求函数f(x)=ax2–2a2x+1(a≠0)在区间
22
y
13
(4)若x∈[ , ],求
22
函数f(x)的最值;
(5)若x∈[t,t+2]时,
求函数f(x)的最值.
t
t +2
–1 0 1 2 3 4 x
y
评注:例1属于“轴
定区间变”的问题,
看作动区间沿x轴移
动的过程中,函数最
t
t +2
值的变化,即动区间
– 1 0 1 2 3 4 x 在定轴的左、右两侧
y
–数f(x)=x2+ax+b,x∈[0,1], 试确定a、b,使f(x)的值域是[0,1].
y
–1 0
1
2
x
总结:求二次函数f(x)=ax2+bx+c在[m,n]上 的最值或值域的一般方法是:
(1)检查x0=
b 2a
是否属于 [ m,n];
(2)当x0∈[m,n]时,f(m)、f(n)、f(x0) 中的较大者是最大值,较小者是最小值;
例1、已知函数f(x)= x2 –2x – 3.
(1)若x∈[–2,0],求函数f(x)的最值;
(2)若x∈[ 2,4],求函数f(x)的最值;
(3)若x∈[ 1 , 5 ],求函数f(x)的最值;
22
y
(4)若x∈[ 1 , 3],求
22
函数f(x)的最值;
(5)若x∈[t,t+2]时, 求函数f(x)的最值.
(1)若x∈[–2,0],求函数f(x)的最值;
(2)若x∈[ 2,4 ],求函数f(x)的最值;
(3)若x∈[ 1 , 5 ],求函数f(x)的最值;
22
y
(4)若x∈[ 1 , 3],
22
求函数f(x)的最值;
1
3
2
2
–1 0 1 2 3 4 x
例1、已知函数f(x)= x2 –2x – 3.
t
t +2
–1 0 1 2 3 4 x
例1、已知函数f(x)= x2 –2x – 3.
(1)若x∈[–2,0],求函数f(x)的最值;
(2)若x∈[ 2,4],求函数f(x)的最值;
(3)若x∈[ 1 , 5 ],求函数f(x)的最值;
22
y
13
(4)若x∈[ , ],求
22
函数f(x)的最值;
及包含定轴的变化,
要注意开口方向及端
点情况。
例2、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
y
–1 0 1 2
x
例2、求函数f(x)=ax2–2a2x+1(a≠0)在区间
[–1,2]上的最值.
y
–1 0 1 2
x
例2、求函数f(x)=ax2–2a2x+1(a≠0)在区间
