第十章 轴
机械基础 第十章 轴

转轴的结构
轴向固定
轴肩 或轴环 轴端 挡圈
圆螺母
轴套
弹性 挡圈 紧定螺钉 与挡圈
圆锥面
能消除轴与轮毂间的径向间隙 ,装拆方便,可兼做周向固定。常 与轮端挡圈联合使用,实现零件的 双向固定。适用于有冲击载荷和对 中性要求较高的场合,常用于轴端 零件的固定。
转轴的结构
轴上零件的周向固定
平键 连接
目的——保证轴能可靠地传递运动和转矩, 防止轴上零件与轴产生相对转动。
目的——保证零件在轴上有确定的轴 向位置,防止零件作轴向移动,并能承受 轴向力。
这是一种常用的轴向固定方法。轴 肩或轴环的过渡圆角半径r小于轴上零 件孔端的圆角半径R或倒角C(即r<R或 r<C),这样才能使轴上零件的端面紧 靠定位面。它具有结构简单,定位可靠 和能够承受较大轴向力等优点,广泛应 用于各种轴上零件的固定。
常用于医疗器械和电动手持小 型机具,例如铰孔接头机、刮削机 等。
轴的用途和分类
直轴的分类及特点
心轴
转动心轴 固定心轴
转动心轴
火车轮轴 固定心轴
自行车前轴
用来支承转动的零件,工作 时只承受弯矩作用而不传递动力 。例如车辆用的转动心轴;支承 滑轮用的固定心轴。
轴的用途和分类
直轴的分类及特点
心轴
转轴
传动齿轮轴
传动轴
发动机曲轴
汽车传动轴
轴的用途和分类
二、轴的分类 根据轴心线形状的不同,可以把轴分为直轴、曲轴和挠性钢丝软轴(简称挠性轴)三大类。 生产及生活中常用的是直轴。根据直轴所受的承载情况不同,又可分为心轴、转轴和传动轴三类。
轴的类型及特点
直轴
光轴 阶梯轴
直轴的轴线为一直线。按直轴 外形不同,又分为光轴(直径无变 化)和阶梯轴(直径有变化)。
2023七年级数学下册第10章轴对称平移与旋转10

形成轴对称图形时,符合条件的角α有
个.
答案
4.3 如图,满足条件的α的值为90°或180°或270°.故符合条件的角α有3个.
5. 如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB'C'D'E',旋转角为
α(0°≤α≤90°).若DE⊥B'C',则α=
°.
答案
5.54 设DE与B'C'相交于O点,如图,∵五边形ABCDE为正五边形,∴∠B=∠BAE=∠E=(5 −2) ABCDE绕点A顺时针旋转后得到正五边形AB'C'D'E',旋转角为 α(0°≤α≤90°),∴∠BAB'=α,∠B'=∠B=108°.∵DE⊥B'C', ∴∠B'OE=90°,∴∠B'AE=360°-∠B'-∠E-∠B'OE=360°-108°-108°-90°=54°,∴∠BAB 54°=54°, ∴α=54°.
课时2 旋转 的特征
知识点1 旋转 的特征
1. 如图,将直角三角形ABC绕着直角顶点C逆时针旋转90°得到直角三角形EFC.若AC=2,
()
A.1
B.1
C.3
D.2
2
2
答案
1.B 根据旋转的特征,得CF=BC=1,所以AF=AC-CF=2-1=1.
知识点1 旋转 的特征
2. 如图,将△ABC绕点A旋转之后得到△ADE,则下列结论不一定正确的是 ( )
2. 如图,直线x⊥y,直线x,y交于点O,点B,C,E在直线y上,直角三角形ABC经过变换得到直 角三角形ODE.若OC=1,AC=2,则这种变换可以是 ( ) A.△ABC绕点C顺时针旋转90°,再向下平移3 B.△ABC绕点C顺时针旋转90°,再向下平移1 C.△ABC绕点C逆时针旋转90°,再向下平移1 D.△ABC绕点C逆时针旋转90°,再向下平移3
华师版七年级数学下册精品课件(HS) 第10章 轴对称、平移与旋转 专题课堂(十) 图形变换的应用

6.(原创题)如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点 A与CB延长线上的点E重合.
(1)三角尺旋转了多少度? (2)连结CD,试判断△CBD的形状; (3)在等腰三角形中存在“两个底角相等”的事实,请用这个结论,求∠BDC的度 数. 解:(1)因为∠ABC=30°,所以∠ABE=180°-∠ABC=180°-30°=150°, 即三角尺旋转了150° (2)因为由旋转的特征可知BC=BD,所以△CBD是等腰三角形 (3)因为△BCD是等腰三角形,所以∠BCD=∠BDC.∴∠DBE=∠BCD+∠BDC= 2∠BDC.又因为由平移的特征知∠DBE=∠CBA=30°,所以2∠BDC=30°,所以 ∠BDC=15°
(3)略
(3)选择图③,④中的一种说明理由.
解:(2)画图如下:
(3)略
分析:(1)由平移的特征可知∠C=∠BED=45°,根据三角形的内角和求出∠A; (2)由平移的特征可得 DE=AF,DE=FC,则 AF=CF=DE=12 AC,可求出 DE; (3)由(2)即可得出结论.
解:(1)∠A=65°,∠C=45° (2)DE=6 cm (3)成立,理由:由平移可得 DE=AF,DE=FC,所以 DE=AF=FC,所以 2DE=AF+FC,所以 2DE=AC, 所以 DE=12 AC
点E处,若∠A=25°,则∠CDE的度数为( C ) A.50° B.65° C.70° D.75°
3.如图,在Rt△ABC中,∠BAC=90°,将△ABC沿直线BC向右平移得到△DEF,
第十章轴对称平移与旋转复习课课件华东师大版七年级数学下册

对称图形也是轴对称图形.
三、考点探究
方法总结 4:
(1)中心对称图形和轴对称图形的主要区别在于一个是绕一点旋转,另 一个是沿一条直线对折. (2)这是易错点,也是辨别它们不同的关键.
〖当堂检测〗
4. 下列说法不正确的是( B ) A. 任何一个具有对称中心的四边形都是平行四边形 B. 平行四边形既是轴对称图形,又是中心对称图形 C. 线段、平行四边形、矩形、菱形、正方形都是中心对称图形 D. 正三角形、矩形、菱形、正方形都是轴对称图形,且对称轴都不止一条.
第十章 轴对称、平移与旋转 复习课
学习导航
学习目标 知识梳理 考点探究 当堂检测 课堂总结
一、学习目标
1.理解图形经过轴对称、平移、旋转后能得到一个与原图形全等 的图形; 2.会画简单图形经过轴对称、平移、旋转后的图形; 3.会用轴对称、平移、旋转、全等的性质解决简单的数学问题.
二、知识梳理
知识点一:轴对称 1. 轴对称图形:把一个图形沿某条直线对折,对折后两部分能完全重合, 这个图形就是轴对称图形,这条直线即为这个图形的对称轴;
考点四 旋转的概念及性质的应用
例 4:如图,将 △AOB 绕点 O 按逆时针方向旋转 60°后得到△COD,若
∠AOB = 15°,则∠AOD的度数是(C )
D C
A. 15 °
B. 60 °
C. 45 ° D. 75 °
分析:抓住旋转前后图形的角度不变,再找出旋转角即可; O 解:已知 △COD 是由 △AOB 旋转得来,且 ∠AOB = 15°;
角的大小不变,变换前后两个图像是全等图形
全等多边形
全等多边形对应边、角分别相等;反之,可做判定.
A. 点A
B. 点B C. 点C D. 点D
华师版七年级数学下册作业课件(HS) 第十章 轴对称、平移与旋转 轴对称 生活中的轴对称

15.(16分)如图,长方形台球桌ABCD上有两个球P,Q. (1)请画出一条路径,使得球P撞击台球桌边AB反弹后,正好撞到球 Q; (2)请画出一条路径,使得球P撞击台球桌边,经过两次反弹后,正 好撞到球Q.
解:(1)如图,运动路径P→M→Q即为所求 (2)如图,运动路径P→E→F→Q即为所求
华师版
第十章 轴对称、平移与旋转
10.1 轴对称 10.1.1 生活中的轴对称
1.(5分)下列“微信表情”中属于轴对称图形的是( A )
A
B
C
D
2.(5分)(泰安中考)下列图形: 是轴对称图形且只有两条对称轴的是( A )
A.①② B.②③ C.②④ D.③④桌面示意 图,图中四个角上的阴影部分分别表示四个入球孔,如果一个 球按图中所示的方向被击出(球可以经过台球边缘多次反弹), 那么球最后将落入的球袋是( A )
即可)
6.(5分)如图,六边形ABCDEF是轴对称图形,直线CF是它的对称 轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD=( B )
A.150° B.300° C.210° D.330°
7.(10分)如图,四边形ABCD与四边形EFGH关于某一条直 线成轴对称,根据图中提供的条件,求x,y的值.
14.(14分)如图,在△ABC中,AD是BC边上的高,将△ABD沿AD所 在直线折叠,得到△AED,点E在CD上,∠B=50°,∠C=30°.
(1)求∠BAD的度数; (2)求∠CAE的度数. 解:(1)由题意知∠BDA=90°,由三角形内角和定理,知∠BAD= 180°-90°-50°=40° (2) 根 据 题 意 , 知 △ ABD 与 △ AED 关 于 AD 所 在 直 线 对 称 , 则 ∠ B = ∠AED. 由三角形外角性质,知∠AED=∠C+∠CAE,所以∠CAE=50°- 30°=20°
澧县五中七年级数学下册第10章轴对称平移与旋转10.1轴对称4设计轴对称图案课件新版华东师大版5

情景导入
我们已经知道了什么是不等式以 及不等式的性质.这节课我们将学习一 元一次不等式及其解法 , 并用它解决 一些实际问题.
• 学习目标 : 〔1〕知道什么是一元一次不等式 , 会解 一元一次不等式.
〔2〕类比一元一次方程的解法来归纳解 一元一次不等式的方式和步骤 , 加深対 化归思想的体会.
如下图 , 图中哪条线段可以由线段 b 经过平 移得到 ?如何进行平移 ?
解 : 线段 c . 可由线段 b 向右 平移 3 格 , 向上平移 2 格得到.
a c
b
d
知识点2 平移作图
例1 如下图 , 平移△ABC , 使点 A 移动到点 A' , 画出平移后的△A'B'C'.
休息时间到啦
同学们,下课休息十分钟。现在是休 息时间,你们休息一下眼睛,
系数化为1得 : x≥8.
08
(2) 2 x≥2x 1
2
3
解 : 去分母得 : 3〔2+x〕≥2〔2x-1〕 ;
去括号得 : 6+3x≥4x-2 ;
移项得 : 3x-4x ≥ -2-6 ; 合并同类项得 : -x ≥ -8 ;
将解集用数轴表 示 , 那么如以下 图:
系数化为1得 : x≤8.
0
8
随堂练习
1.用四块如下图的瓷砖拼成一个正方形 , 形成轴对称的图案 , 和自己的同伴比一比 , 看 谁的拼法多.
七年级数学下册第10章轴对称平移与旋 转10.1轴对称4设计轴对称图案课件新 版华东师大版5
同学们,下课休息十分钟。现在是休
息时间,你们休息一下眼睛,
看看远处,要保护好眼睛哦~站起来 动一动,久坐对身体不好哦~
华东师大版数学七年级下册第十章《轴对称、平移与旋转》全单元课件

第10章 轴对称、平移与 旋转
10.1 轴对称
10.1.1 生活中的轴对称
导入新课 讲授新课 当堂练习 课堂小结
学习目标
1.经历观察轴对称现象的过程,探索轴对称现象共同特征.(重点)
2.认识轴对称,能够识别简单的轴对称图形及其对称轴.(难点)
导入新课
讲授新课
轴对称和轴对称图形
性质 定 义
轴对称
成轴对 称图形 性质 联 系 轴对称与成 轴 对 称 区别
课后作业
见本课时练习
七年级数学下(HS) 教学课件
10.1 轴对称
10.1.2 轴对称的再认识
导入新课 讲授新课 当堂练习 课堂小结
学习目标
1.探索轴对称现象共同特点.(重点)
2.轴对称图形与垂直平分线的联系.(重点)
轴对称 图形
a
轴对称 图形
m
对称轴
对称轴
如果一个图形沿一条直线折叠,对折后的两部分能完全重 合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
想一想:
折叠后重合的点是对应点,叫做对称点.
如图点A、A ′就是一对对称点. 下面的每对图形有什么共同特点?
A
A′
B
B′ C 对称轴 C′
对称轴
把一个图形沿一条直线折叠,如果它能够与另一个图形重 合,那么就说这两个图形成轴对称,这条直线就是它的对称轴.
课后作业
见本课时练习
七年级数学下(HS) 教学课件
10.1 轴对称
10.1.3 画轴对称图形
导入新课 讲授新课 当堂练习 课堂小结
学习目标
1.能够按要求画简单平面图形经过一次对称后的图形.(难点) 2.掌握作轴对称图形的方法.(重点)
初中数学华师大版七年级下学期第10章 轴对称、平移与旋转测试卷(含解析)
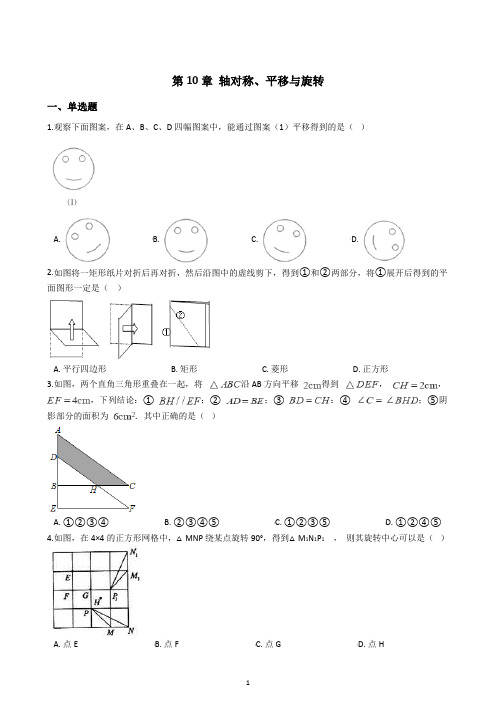
第10章轴对称、平移与旋转一、单选题1.观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)平移得到的是()A. B. C. D.2.如图将一矩形纸片对折后再对折,然后沿图中的虚线剪下,得到①和②两部分,将①展开后得到的平面图形一定是()A. 平行四边形B. 矩形C. 菱形D. 正方形3.如图,两个直角三角形重叠在一起,将沿AB方向平移得到,,,下列结论:① ;② ;③ :④ ;⑤阴影部分的面积为.其中正确的是()A. ①②③④B. ②③④⑤C. ①②③⑤D. ①②④⑤4.如图,在4×4的正方形网格中,△MNP绕某点旋转90°,得到△M1N1P1,则其旋转中心可以是()5.下列银行标志是中心对称图形的是()A. B. C. D.6.如图,在边长为1的小正力形组成的网格中,点A,B,C部在格点上,若将线段AB沿BC方向平移,使点B与点C重合,则线段AB扫过的面积为()A. 11B. 10C. 9D. 87.如图,在△ABC中,BC=5,∠A=80°,∠B=70°,把△ABC沿RS的方向平移到△DEF的位置,若CF=4,则下列结论中错误的是( )A. BE=4B. ∠F=30°C. AB∥DED. DF=58.如图,沿射线方向平移到(点E在线段上),如果,,那么平移距离为()A. 3cmB. 5cmC. 8cmD. 13cm9.如图,是一个纸折的小风车模型,将它绕着旋转中心旋转下列哪个度数后不能与原图形重合.()A. B. C. D.10.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列四个结论:①AC=AD;②AB⊥EB;③BC=EC;④∠A=∠EBC;其中一定正确的是()A. ①②B. ②③C. ③④D. ②③④11.如图,将(其中,),绕点按顺时针方向旋转到的位置,使得点,,在同一直线上,则旋转角的度数为( )A. B. C. D.12.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=4,则BE的长为( )A. 3B. 4C. 5D. 613.图中的两个梯形成中心对称,点P的对称点是()A. 点AB. 点BC. 点CD. 点D14.如图,已知图形是中心对称图形,则对称中心是()A. 点CB. 点DC. 线段BC的中点D. 线段FC的中点15.下列说法中,正确的有()①正方形都是全等形;②等边三角形都是全等形;③形状相同的图形是全等形;④大小相同的图形是全等形;⑤能够完全重合的图形是全等形.A. 1个B. 2个C. 3个D. 4个二、填空题16.如图,将矩形ABCD沿DE折叠,使A点落在BC上的F处,若∠EFB=60°,则∠CFD=________.17.如图,将周长为12的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为________18.如图,在正方形ABCD中,,点E在CD边上,且,将绕点A顺时针旋转90°,得到,连接,则线段的长为________.19.如图,图中有6个条形方格图,图上由实线围成的图形是全等形的有哪几对.20.如图,△DEF是由△ABC沿BC方向向右平移2cm后得到,若△ABC的周长为10cm,则四边形ABFD的周长等于________ cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、轴的结构和轴上零件的固定
3)轴上有切制螺纹要求时,应有退刀槽,以便于螺纹 车刀退出;需要磨削的阶台轴,应留有越程槽,使磨削用砂轮 可越过工作表面。螺纹退刀槽取宽度b≥2P(P为螺距)。越程 槽取宽度b=2~4mm,深度a=0.5~1mm。轴上有多个退刀槽 或越程槽时,应尽可能取相同的尺寸,以方便加工。
二、轴的结构和轴上零件的固定
3)用圆锥销和紧定螺钉作周向固定
二、轴的结构和轴上零件的固定
(3)轴的结构工艺性
1)阶台轴的直径应该是中间大,两端小,由中间向两 端依次减小,便于轴上零件的装拆。
2)轴端、轴颈与轴肩(或轴环)的过渡部位应有倒角 和过渡圆角,以便于轴上零件的装配、避免划伤配合表面,减 少应力集中。轴肩(或轴环)的过渡圆角半径应小于轴上安装 零件内孔的倒角高度或圆角半径,以保证轴上零件端面可靠贴 合轴肩端面。轴上有多处圆角和倒角时,应尽可能使圆角半径 相同和倒角大小一致,以便于加工,减少刀具规格和换刀次数。 自由表面的轴肩过渡圆角不受装配的限制,可取得大些(一般 取r=0.1d),以减少应力集中。
一、轴的分类和应用
转轴(既承受弯矩又承受扭矩 既起支撑作用又起传递作用)
二、轴的结构和轴上零件的固定
1.轴的结构 装配轴承的部分称为轴颈 装配回转零件的部分称为轴头 连接轴头与轴身的部位称为轴身 轴上截面尺寸变化的部分称为轴肩或轴环
2. 轴结构的一般要求 在考虑轴的结构时,应满足下述三个方面的要求: (1)、轴上的零件应有可靠的轴向、周向固定 (2)、便于加工和尽量避免和减小应力集中 (3)、便于轴上零件的安装和拆卸。
二、轴的结构和轴上零件的固定
2)用过盈配合作固向固定 用过盈配合作周向固定主要用于不拆卸的轴与轮毂的连结。 由于包容件轮毂的配合尺寸(孔径)小于被包容件轴的配合尺 寸(轴颈直径),装配后在两者之间产生压力,工作时依靠此 压力所产生的摩擦力来传递转矩。这种连结结构简单,对轴的 削弱小,对中性好,能承受较大的载荷和有较好的抗冲击性能。 其承载能力与抗冲击能力取决于过盈量的大小和配合表面的表 面质量。因此,配合面的加工精度要求高,表面粗糙度值小。 对于对中性要求高、承受较大振动和冲击载荷的周向固定, 可采用键连结与过盈配合组合的固定方法,以传递大的转矩和 使轴上零件的周向固定更牢固,工作过程安全可靠。
二、轴的结构和轴上零件的固定
4)当轴上装有质量较大的零件或与轴颈过盈配合的零 件时,在装入端应加工出半锥角为10°的导向锥面,以便于装 配。
5)为了便于轴 的加工,必要时应设 置中心孔。
二、轴的结构和轴上零件的固定
2.轴上零件的固定(轴向和周向固定) (1)轴上零件的轴向固定
用轴肩和轴环固定
应使轴肩或轴环的过渡圆 角半径r小于轴上零件的 圆角半径R或倒角C 这样才能使轴上零件的断 面紧靠定位面。
二、轴的结构和轴上零件的固定
用圆螺母固定
二、轴的结构和轴上零件的固定
用轴套固定
二、轴的结构和轴上零件的固定
第十章 轴
一、轴的分类和应用 二、轴的结构和轴上零件的固定
第八章 轴系零件
节目录
一、轴的分类和应用
按照轴的轴线形状不同,轴可以分为直轴、曲轴和挠性轴三大类。
一、轴的分类和应用
根据轴所受载荷不同,可将轴分为心轴、转轴和传动轴三类。
心轴(只承受弯矩,起支撑作用)
一、轴的分类和应用
传动轴(只和轴上零件的固定
用弹性挡圈固定
二、轴的结构和轴上零件的固定
(2)轴上零件的周向固定
1)用键作周向固定
键连结用作轴上零件的周向固定形式应用最广。用平键连 结作周向固定,结构简单,制造容易,装拆方便和对中性好, 可用于较高精度、较高转速及受冲击或变载荷作用下的固定连 接,因此应用最普遍,应用平键连结时,对于同一轴上轴径相 差不大的轴颈上的键槽,应尽可能采用同一规格的键槽尺寸, 并使键槽位于相同的角向位置上,以方便加工。用楔键连结作 周向固定,在传递转矩的同时,还能承受单向的轴向力,但对 中性较差。用花键连结作周向固定,具有较高的承载能力,对 中性与导向性均好,但花键制造较困难,成本高。
