2007年全国初中数学竞赛(海南赛区)初赛试题及答案
全国初中数学竞赛(海南赛区)初赛试题(含答案)

11、(3x-2y)212、 13、2 14、3 15、2<x<7
16、13.5 17、1或7 18、5
答案提示:
12、
13、由 得 所以有 所以x的值为2.
因为关于x的方程x2-4x+a=0的两个实数根为x1、x2,由根与系数的关系得x1+x2=4,所以 ,解得 ,所以a=3.
全国初中数学竞赛(海南赛区)
数学试卷
(本试卷共4页,满分120分,考试时间:3月10日8:30——10:30)
题号
一
二
三
总分
(1—10)
(11—18)
19
20
得分
一、选择题(本大题满分50分,每小题5分)
在下列各题的四个备选答案中,只有一个是正确的,请把你认为正确的答案的字母
代号填写在下表相应题号下的方格内
8、由矩形AOBC的面积为8,可求矩形PEOF的面积为2,
又点P在第一象限,所以K=2,故选择B.
9、如图,分别以大的正方形中间”十”字所在的直线为对称轴可画出2、3两图,分别以正方形对角线所在直线为对称轴可画出4、5两图,再加上第1幅图,总共有5个符合条件的三角形,故选择A.
10、若点M在圆上,点M与圆心A的距离等于圆的半径 ,容易判断点(2,0)是圆A与X轴正半轴的交点、点(0,-2)是圆A与y轴负半轴的交点,另外,可以通过构造直角三角形判断点(2,-2)与圆心A的距离等于 ,也可以用两点公式求出点(2,-2)与圆心A的距离等于 ,因此A、B、C三个选项中的点均在圆上,而点(1,-2)与圆心A的距离等于1,小于圆A的半径,点(1,-2)不在圆上,故选择D.
19、海南省某种植园收获香蕉20000千克,其中香牙蕉12000千克、黄帝蕉8000千克,准备运往海口与文昌销售;根据市场供需,海口需要香蕉15000千克,文昌需要香蕉5000千克,海口与文昌两地的香蕉售价如下表所示:
2007年全国初中数学竞赛(初赛)试题
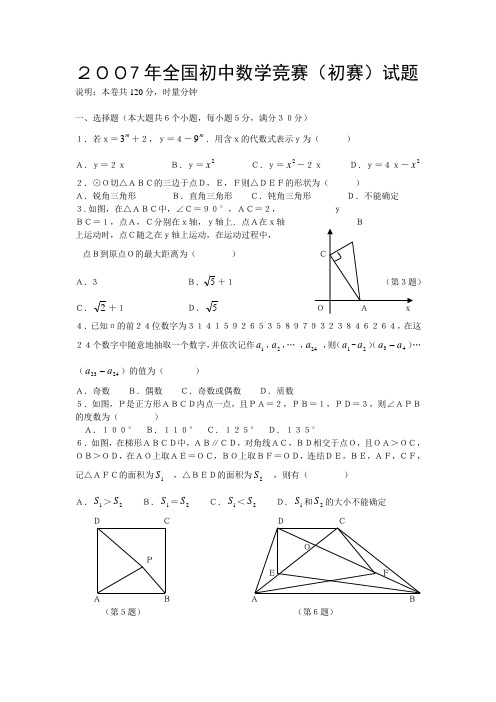
2007年全国初中数学竞赛(初赛)试题说明:本卷共120分,时量分钟一、选择题(本大题共6个小题,每小题5分,满分30分)1.若x=m3+2,y=4-m 9.用含x的代数式表示y为( )A.y=2x B.y=2x C.y=2x -2x D.y=4x-2x 2.⊙O切△ABC的三边于点D,E,F则△DEF的形状为( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定 3.如图,在△ABC中,∠C=90°,AC=2, yBC=1,点A,C分别在x轴,y轴上.点A在x轴 B上运动时,点C随之在y轴上运动,在运动过程中, 点B到原点O的最大距离为( ) A.3 B.5+1 C.2+1 D.5 4.已知π的前24位数字为314159265358979323846264,在这24个数字中随意地抽取一个数字,并依次记作1a ,2a ,… ,24a ,则(1a -2a )(43a a -)…(2423a a -)的值为( )A.奇数 B.偶数 C.奇数或偶数 D.质数5.如图,P是正方形ABCD内点一点,且PA=2,PB=1,PD=3,则∠APB的度数为( )A.100° B.110° C.125° D.135°6.如图,在梯形ABCD中,AB∥CD,对角线AC,BD相交于点O,且OA>OC,OB>OD,在AO上取AE=OC,BO上取BF=OD,连结DE,BE,AF,CF,记△AFC的面积为1S ,△BED的面积为2S ,则有( )A.1S >2S B.1S =2S C.1S <2S D.1S 和2S 的大小不能确定 D C D C O P E FA B A B(第5题)(第6题)二、填空题(本大题共6个小题,每小题5分,满分30分) 7.一个凸多边形的所有内角中,最多有( )个锐角. 8.已知a 1-a =1,那么代数式a1+a 的值为( ). 9.为了了解用电量的多少,小明在3月初连续几天同一时刻观察电表显示的刻度数,记录如下表:由此可以估计小明3月份的用电量大约是( )度. 10.若分式方程22-+x ax =-1的解是正数,则a的取值范围是( ) 11.如图,六面体的4个定点处分别有四只 A蚂蚁1A ,2A ,3A ,4A ,要求它们在爬过所有 A 2A 的9条棱后到达终点B,如果它们的爬速相同,那么最先到达终点的是( ). B12.已知二次函数y=a2x +bx+c和一次函数y=k(x-1)-42k ,若它们的图像对任意实数k都只有一个公共点,则该二次函数的解析式为( )三、解答题(本大题共4个小题,每小题15分,满分60分)13.若多项式2x -(a+5)x+5a-1能分解成两个一次因式x+b,x+c的乘积(要求b,c是整数且b<c),求a,b,c的值.14.如图,已知正方形ABCD的边长为1,G为CD边上的一个动点(点G不与C,D重合)以CG为边在正方形ABCD外作正方形GCEF连结DE交BG的延长线于点H.⑴求证:△BCG≌△DEC⑵BH与DE垂直吗?证明你的结论.⑶当点G运动到什么位置时,BH垂直平分DE?请说明理由.ADHGFBCE15.今有甲,乙两个游团取某公园游览,若分别购票,两团总计应付门票费13140元;若合在一起作为一个团队购票,总计应付门票费10080元,问这两个游团各有多少人?附:公园门票价格购票人数1~50人51~100人100人以上每人门票价格130元110元90元16.如图,AB是⊙O的直径,C是半径OB的中点,D是OB延长线上的一点,且BD=OB,过D的直线交⊙O于M,E,连结MB.(1)求证:MB平分∠CMD;(2)求MD︰MC的值;(3)当MD与⊙O相切时,MD︰MC的值是否发生变化?请说明理由.。
2007年全国初中数学联合竞赛试题及详细解答(含一试二试)

2007年全国初中数学联合竞赛试题第一试一、选择题(本题满分42分,每小题7分)本题共有6小题,每题均给出了代号为D C B A ,,,的四个答案,其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每小题选对得7分;不选、选错或选出的代号字母超过一个(不论是否写在括号内),一律得0分.1. 已知z y x ,,满足xz z y x +=-=532,则z y yx 25+-的值为 ( )(A )1. (B )31. (C )31-. (D )21.2.当x 分别取值20071,20061,20051,…,21,1,2,…,2005,2006,2007时,计算代数式2211x x +-的值,将所得的结果相加,其和等于 ( )(A )-1. (B )1. (C )0. (D )2007.3. 设c b a ,,是△ABC 的三边长,二次函数2)2(2ba cx xb a y ----=在1=x 时取最小值b 58-,则△ABC 是 ( ) (A )等腰三角形. (B )锐角三角形. (C )钝角三角形. (D )直角三角形.4. 已知锐角△ABC 的顶点A 到垂心H 的距离等于它的外接圆的半径,则∠A 的度数是( )(A )30°. (B )45°. (C )60°. (D )75°.5.设K 是△ABC 内任意一点,△KAB 、△KBC 、△KCA 的重心分别为D 、E 、F ,则ABC DEF S S △△:的值为 ( )(A )91. (B )92. (C )94. (D )32.6.袋中装有5个红球、6个黑球、7个白球,从袋中摸出15个球,摸出的球中恰好有3个红球的概率是 ( )(A )101. (B )51. (C )103. (D )52.二、填空题(本题满分28分,每小题7分) 1. 设121-=x ,a 是x 的小数部分,b 是x -的小数部分,则=++ab b a 333______.2. 对于一切不小于2的自然数n ,关于x 的一元二次方程22(2)20x n x n -+-=的两个根记作n n b a ,(2≥n ),则)2)(2(122--b a )2)(2(133--+b a Λ+)2)(2(120072007--+b a =3. 已知直角梯形ABCD 的四条边长分别为6,10,2====AD CD BC AB ,过B 、D 两点作圆,与BA 的延长线交于点E ,与CB 的延长线交于点F ,则BF BE -的值为______..4. 若64100+a 和64201+a 均为四位数,且均为完全平方数,则整数a 的值是______第二试 (A )一、 (本题满分20分)设n m ,为正整数,且2≠m ,如果对一切实数t ,二次函数mt x mt x y 3)3(2--+=的图象与x 轴的两个交点间的距离不小于2t n +,求n m ,的值.ABCDE F G M N二、(本题满分25分)如图,四边形ABCD 是梯形,点E 是上底边AD 上一点,CE 的延长线与BA 的延长线交于点F ,过点E 作BA 的平行线交CD 的延长线于点M ,BM 与AD 交于点N .证明:∠AFN =∠DME .三、 (本题满分25分)已知a 是正整数,如果关于x 的方程056)38()17(23=--+++x a x a x 的根都是整数,求a 的值及方程的整数根. A B C D E F MN P一、(本题满分20分)设n m ,为正整数,且2≠m ,二次函数mt x mt x y 3)3(2--+=的图象与x 轴的两个交点间的距离为1d ,二次函数nt x n t x y 2)2(2+-+-=的图象与x 轴的两个交点间的距离为2d .如果21d d ≥对一切实数t 恒成立,求n m ,的值二、(本题满分25分)题目和解答与(A )卷第二题相同. .三、(本题满分25分)设a 是正整数,二次函数a x a x y -+++=38)17(2,反比例函数xy 56=,如果两个函数的图象的交点都是整点(横坐标和纵坐标都是整数的点),求a 的值.一、(本题满分25分)题目和解答与(B )卷第一题相同. 二、(本题满分25分)题目和解答与(A )卷第二题相同.三、(本题满分25分)设a 是正整数,如果二次函数a x a x y 710)232(22-+++=和反比例函数xay 311-=的图象有公共整点(横坐标和纵坐标都是整数的点),求a 的值和对应的公共整点.2007年全国初中数学联合竞赛 试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请严格按照本评分标准规定的评分档次给分,不要再增加其他中间档次.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试一、选择题(本题满分42分,每小题7分)本题共有6小题,每题均给出了代号为D C B A ,,,的四个答案,其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每小题选对得7分;不选、选错或选出的代号字母超过一个(不论是否写在括号内),一律得0分. 1. 已知z y x ,,满足xz z y x +=-=532,则z y yx 25+-的值为 ( )(A )1. (B )31. (C )31-. (D )21. 【答】B. 解 由x z z y x +=-=532得x z x y 23,3==,所以31333525=+-=+-x x x x z y y x ,故选(B ). 注:本题也可用特殊值法来判断.2.当x 分别取值20071,20061,20051,…,21,1,2,…,2005,2006,2007时,计算代数式2211xx +-的值,将所得的结果相加,其和等于 ( ) (A )-1. (B )1. (C )0. (D )2007. 【答】C.解 因为=+-++-222211)1(1)1(1n n nn 011112222=+-++-n n n n ,即当x 分别取值n 1,n n (为正整数)时,计算所得的代数式的值之和为0;而当1=x 时,0111122=+-.因此,当x 分别取值20071,20061,20051,…,21,1,2,…,2005,2006,2007时,计算所得各代数式的值之和为0.故选(C ). 3. 设c b a ,,是△ABC 的三边长,二次函数2)2(2b a cx x b a y ----=在1=x 时取最小值b 58-,则△ABC 是 ( )(A )等腰三角形. (B )锐角三角形. (C )钝角三角形. (D )直角三角形. 【答】D.解 由题意可得⎪⎪⎩⎪⎪⎨⎧-=----=---,5822,1)2(2b b a c b a b a c 即⎪⎩⎪⎨⎧==+,53,2b c a c b 所以b c 53=,b a 54=,因此222b c a =+,所以△ABC 是直角三角形. 故选(D ).4. 已知锐角△ABC 的顶点A 到垂心H 的距离等于它的外接圆的半径,则∠A 的度数是( )(A )30°. (B )45°. (C )60°. (D )75°.【答】C.解 锐角△ABC 的垂心在三角形内部,如图,设△ABC 的外心为O ,D 为BC 的中点,BO 的延长线交⊙O 于点E ,连CE 、AE ,则CE //AH ,AE //CH ,则OD CE AH OB 2===,所以∠OBD =30°,∠BOD =60°,所以∠A =∠BOD =60°.故选(C ). 5.设K 是△ABC 内任意一点,△KAB 、△KBC 、△KCA 的重心分别为D 、E 、F ,则ABC DEF S S △△:的值为 ( )(A )91. (B )92. (C )94. (D )32. 【答】A.解 分别延长KD 、KE 、KF ,与△ABC 的三边AB 、BC 、CA 交于点M 、N 、P ,由于D 、E 、F 分别为△KAB 、△KBC 、△KCA 的重心,易知M 、N 、P 分别为AB 、BC 、CA 的中点,所以ABC MNP S S △△41=. 易证△DEF ∽△MNP ,且相似比为3:2,所以MNP DEF S S △△2)32(=ABC S △4194⋅=ABC S △91=. 所以:DEF S △19ABC S =△.故选(A ). 6.袋中装有5个红球、6个黑球、7个白球,从袋中摸出15个球,摸出的球中恰好有3个红球的概率是 ( )(A )101. (B )51. (C )103. (D )52.【答】B.解 设摸出的15个球中有x 个红球、y 个黑球、z 个白球,则z y x ,,都是正整数,且7,6,5≤≤≤z y x ,15=++z y x .因为13≤+z y ,所以x 可取值2,3,4,5.当2=x 时,只有一种可能,即7,6==z y ;当3=x 时,12=+z y ,有2种可能,7,5==z y 或6,6==z y ;当4=x 时,11=+z y ,有3种可能,7,4==z y 或6,5==z y 或5,6==z y ;当5=x 时,10=+z y ,有4种可能,7,3==z y 或6,4==z y 或5,5==z y 或4,6==z y . 因此,共有1+2+3+4=10种可能的摸球结果,其中摸出的球中恰好有3个红球的结果有2种,所以所求的概率为51102=.故选(B ). 二、填空题(本题满分28分,每小题7分) 1. 设121-=x ,a 是x 的小数部分,b 是x -的小数部分,则=++ab b a 333____1___.解 ∵12121+=-=x ,而3122<+<,∴122-=-=x a .又∵12--=-x ,而2123-<--<-,∴22)3(-=---=x b .∴1=+b a ,∴=++ab b a 333=++-+ab b ab a b a 3))((221)(3222=+=++-b a ab b ab a .2. 对于一切不小于2的自然数n ,关于x 的一元二次方程22(2)20x n x n -+-=的两个根记作n n b a ,(2≥n ),则)2)(2(122--b a )2)(2(133--+b a Λ+)2)(2(120072007--+b a =.10034016-解 由根与系数的关系得2+=+n b a n n ,22n n a b n ⋅=-,所以=--)2)(2(n n b a (2-n n b a 4)++n n b a 222(2)42(1)n n n n =--++=-+,则11111()(2)(2)2(1)21n n a b n n n n =-=----++,)2)(2(122--b a )2)(2(133--+b a Λ+)2)(2(120072007--+b a=11111111111003()()()()22334200720082220084016⎡⎤--+-++-=--=-⎢⎥⎣⎦L . 3. 已知直角梯形ABCD 的四条边长分别为6,10,2====AD CD BC AB ,过B 、D 两点作圆,与BA 的延长线交于点E ,与CB 的延长线交于点F ,则BF BE -的值为____4_____.解 延长CD 交⊙O 于点G ,设DG BE ,的中点分别为点N M ,,则易知DN AM =.因为10==CD BC ,由割线定理,易证DGBF =,所以42)(2)(2==-=-=-=-AB AM BM DN BM DG BE BF BE .4. 若64100+a 和64201+a 均为四位数,且均为完全平方数,则整数a 的值是___17____. 解 设264100m a =+,264201n a =+,则100,32<≤n m ,两式相减得))((10122m n m n m n a -+=-=,因为101是质数,且101101<-<-m n ,所以101=+m n ,A BCD EF GM N故1012-=-=n m n a .代入264201n a =+,整理得020*******=+-n n ,解得59=n ,或343=n (舍去).所以171012=-=n a .第二试 (A )一、 (本题满分20分)设n m ,为正整数,且2≠m ,如果对一切实数t ,二次函数mt x mt x y 3)3(2--+=的图象与x 轴的两个交点间的距离不小于2t n +,求n m ,的值.解 因为一元二次方程03)3(2=--+mt x mt x 的两根分别为mt 和3-,所以二次函数mt x mt x y 3)3(2--+=的图象与x 轴的两个交点间的距离为3mt +.由题意,32mt t n +≥+,即22(3)(2)mt t n +≥+,即222(4)(64)90m t m n t n -+-+-≥.由题意知,042≠-m ,且上式对一切实数t 恒成立,所以⎪⎩⎪⎨⎧≤----=∆>-,0)9)(4(4)46(,042222n m n m m 22,4(6)0,m mn >⎧⇒⇒⎨-≤⎩⎩⎨⎧=>,6,2mn m 所以⎩⎨⎧==,2,3n m 或⎩⎨⎧==.1,6n m 二、(本题满分25分)如图,四边形ABCD 是梯形,点E 是上底边AD 上一点,CE 的延长线与BA 的延长线交于点F ,过点E 作BA 的平行线交CD 的延长线于点M ,BM 与AD 交于点N .证明:∠AFN =∠DME .证明 设MN 与EF 交于点P ,∵NE //BC , ∴△PNE ∽△PBC ,∴PCPEPB PN =, ∴PC PN PE PB ⋅=⋅.又∵ME //BF ,∴△PME ∽△PBF ,∴PFPEPB PM =, ∴PF PM PE PB ⋅=⋅. ∴PF PM PC PN ⋅=⋅,故PFPCPN PM = 又∠FPN =∠MPE ,∴△PNF ∽△PMC ,∴∠PNF =∠PMC ,∴NF//MC ∴∠ANF =∠EDM.AB CDEFMN P∴∠ANF +∠FAN =∠EDM +∠MED ,∴∠AFN=∠DME.三、 (本题满分25分)已知a 是正整数,如果关于x 的方程056)38()17(23=--+++x a x a x 的根都是整数,求a 的值及方程的整数根.解 观察易知,方程有一个整数根11=x ,将方程的左边分解因式,得[]056)18()1(2=+++-x a x x因为a 是正整数,所以关于x 的方程056)18(2=+++x a x (1)的判别式0224)18(2>-+=∆a ,它一定有两个不同的实数根.而原方程的根都是整数,所以方程(1)的根都是整数,因此它的判别式224)18(2-+=∆a 应该是一个完全平方数.设22224)18(k a =-+(其中k 为非负整数),则224)18(22=-+k a ,即224)18)(18(=-+++k a k a .显然k a ++18与k a -+18的奇偶性相同,且1818≥++k a ,而8284562112224⨯=⨯=⨯=,所以⎩⎨⎧=-+=++,218,11218k a k a 或⎩⎨⎧=-+=++,418,5618k a k a 或⎩⎨⎧=-+=++,818,2818k a k a 解得⎩⎨⎧==,55,39k a 或⎩⎨⎧==,26,12k a 或⎩⎨⎧==,10,0k a 而a 是正整数,所以只可能⎩⎨⎧==,55,39k a 或⎩⎨⎧==.26,12k a当39=a 时,方程(1)即056572=++x x ,它的两根分别为1-和56-.此时原方程的三个根为1,1-和56-.当12=a 时,方程(1)即056302=++x x ,它的两根分别为2-和28-.此时原方程的三个根为1,2-和28-.第二试 (B )一、(本题满分20分)设n m ,为正整数,且2≠m ,二次函数mt x mt x y 3)3(2--+=的图象与x 轴的两个交点间的距离为d ,二次函数nt x n t x y 2)2(2+-+-=的图象与x 轴的两个交点间的距离为2d .如果21d d ≥对一切实数t 恒成立,求n m ,的值.解 因为一元二次方程03)3(2=--+mt x mt x 的两根分别为mt 和3-,所以31+=mt d ; 一元二次方程02)2(2=+-+-nt x n t x 的两根分别为t 2和n -,所以n t d +=22.所以,21d d ≥22)2()3(23n t mt n t mt +≥+⇔+≥+⇔ 09)46()4(222≥-+-+-⇔n t n m t m (1)由题意知,042≠-m ,且(1)式对一切实数t 恒成立,所以⎪⎩⎪⎨⎧≤----=∆>-,0)9)(4(4)46(,042222n m n m m 22,4(6)0,m mn >⎧⇒⇒⎨-≤⎩⎩⎨⎧=>,6,2mn m 所以⎩⎨⎧==,2,3n m 或⎩⎨⎧==.1,6n m 二、(本题满分25分)题目和解答与(A )卷第二题相同. 三、(本题满分25分)设a 是正整数,二次函数a x a x y -+++=38)17(2,反比例函数xy 56=,如果两个函数的图象的交点都是整点(横坐标和纵坐标都是整数的点),求a 的值. 解 联立方程组⎪⎩⎪⎨⎧=-+++=,56,38)17(2x y a x a x y 消去y 得a x a x -+++38)17(2x 56=,即 056)38()17(23=--+++x a x a x ,分解因式得[]056)18()1(2=+++-x a x x (1)显然11=x 是方程(1)的一个根,(1,56)是两个函数的图象的一个交点.因为a 是正整数,所以关于x 的方程 056)18(2=+++x a x (2)的判别式0224)18(2>-+=∆a ,它一定有两个不同的实数根.而两个函数的图象的交点都是整点,所以方程(2)的根都是整数,因此它的判别式224)18(2-+=∆a 应该是一个完全平方数.设22224)18(k a =-+(其中k 为非负整数),则224)18(22=-+k a ,即 224)18)(18(=-+++k a k a .显然k a ++18与k a -+18的奇偶性相同,且1818≥++k a ,而8284562112224⨯=⨯=⨯=,所以⎩⎨⎧=-+=++,218,11218k a k a 或⎩⎨⎧=-+=++,418,5618k a k a 或⎩⎨⎧=-+=++,818,2818k a k a 解得⎩⎨⎧==,55,39k a 或⎩⎨⎧==,26,12k a 或⎩⎨⎧==,10,0k a 而a 是正整数,所以只可能⎩⎨⎧==,55,39k a 或⎩⎨⎧==.26,12k a 当39=a 时,方程(2)即056572=++x x ,它的两根分别为1-和56-,此时两个函数的图象还有两个交点)56,1(--和)1,56(--.当12=a 时,方程(2)即056302=++x x ,它的两根分别为2-和28-,此时两个函数的图象还有两个交点)28,2(--和)2,28(--.第二试 (C )一、(本题满分25分)题目和解答与(B )卷第一题相同.二、(本题满分25分)题目和解答与(A )卷第二题相同.三、(本题满分25分)设a 是正整数,如果二次函数a x a x y 710)232(22-+++=和反比例函数xa y 311-=的图象有公共整点(横坐标和纵坐标都是整数的点),求a 的值和对应的公共整点. 解 联立方程组⎪⎩⎪⎨⎧-=-+++=,311,710)232(22x a y a x a x y 消去y 得a x a x 710)232(22-+++= 113a x-,即0113)710()232(223=-+-+++a x a x a x ,分解因式得 []0311)12()12(2=-+++-a x a x x (1)如果两个函数的图象有公共整点,则方程(1)必有整数根,从而关于x 的一元二次方程 0311)12(2=-+++a x a x (2)必有整数根,所以一元二次方程(2)的判别式∆应该是一个完全平方数,而224)18(10036)311(4)12(222-+=++=--+=∆a a a a a .所以224)18(2-+a 应该是一个完全平方数,设22224)18(k a =-+(其中k 为非负整数),则224)18(22=-+k a ,即224)18)(18(=-+++k a k a .显然k a ++18与k a -+18的奇偶性相同,且1818≥++k a ,而8284562112224⨯=⨯=⨯=,所以⎩⎨⎧=-+=++,218,11218k a k a 或⎩⎨⎧=-+=++,418,5618k a k a 或⎩⎨⎧=-+=++,818,2818k a k a 解得⎩⎨⎧==,55,39k a 或⎩⎨⎧==,26,12k a 或⎩⎨⎧==,10,0k a 而a 是正整数,所以只可能⎩⎨⎧==,55,39k a 或⎩⎨⎧==.26,12k a 当39=a 时,方程(2)即0106512=-+x x ,它的两根分别为2和53-,易求得两个函数的图象有公共整点)53,2(-和)2,53(-.当12=a 时,方程(2)即025242=-+x x ,它的两根分别为1和25-,易求得两个函数的图象有公共整点)25,1(-和)1,25(-.------------------------------------------------------------------------怎样才能学好数学一、把握好课堂的每一分钟如今的小学数学教师,都比较重视课堂教学的效益,所以,老师最期盼的事情就是:学生能够专心听讲,眼睛时刻盯在老师身上,或者盯在黑板上。
2007年全国初中数学竞赛试题及参考答案

中国教育学会中学数学教学专业委员会 2007年全国初中数学竞赛试题参考答案一、选择题(共5小题,每小题6分,满分30分。
以下每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里。
不填、多填或错填得零分)1、方程组⎩⎨⎧=+=+6||12||y x y x 的解的个数为( )A 、1B 、 2C 、3D 、4 答案:A解析:若0≥x ,则⎩⎨⎧=+=+6||12y x y x ,于是6||-=-y y ,显然不可能若0 x ,则⎩⎨⎧=+=+-6||12y x y x于是18||=+y y ,解得9=y ,进而求得3-=x 所以,原方程组的解为⎩⎨⎧=-=93y x ,只有1个解.故选(A ).2、口袋中有20个球,其中白球9个,红球5个,黑球6个.现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数是( )A 、 14B 、 16C 、18D 、20答案:B解析:用枚举法:红球个数 白球个数 黑球个数 种 数 5 2,3,4,5 3,2,1,0 4 4 3,4,5,6 3,2,1,0 4 3 4,5,6,7 3,2,1,0 4 2 5,6,7,8 3,2,1,0 4 所以,共16种. 故选(B ).3、已知ABC ∆为锐角三角形,⊙O 经过点B ,C ,且与边AB ,AC 分别相交于点D ,E . 若⊙O 的半径与ADE ∆的外接圆的半径相等,则⊙O 一定经过ABC ∆的( )A 、内心B 、外心C 、重心D 、垂心 答案:B解析: 如图,连接BE ∵ABC ∆为锐角三角形 ∴BAC ∠,ABE ∠均为锐角又∵⊙O 的半径与ADE ∆的外接圆的半径相等,且DE 为两圆的公共弦 ∴ABE BAC ∠=∠∴BAC ABE BAC BEC ∠=∠+∠=∠2 若ABC ∆的外心为1O 则BAC C BO ∠=∠21 ∴⊙O 一定过ABC ∆的外心 故选(B ).4、已知三个关于x 的一元二次方程02=++c bx ax ,02=++a cx bx ,02=++b ax cx 恰有一个公共实数根,则abc ca b bc a 222++的值为( ) A 、0 B 、1 C 、2 D 、3 答案:D解析:设0x 是它们的一个公共实数根,则02=++c bx ax ,02=++a cx bx ,02=++b ax cx把上面三个式子相加,并整理得()()01020=++++x x c b a因为0432112002+⎪⎭⎫ ⎝⎛+=++x x x所以0=++c b a于是()()33333333222=+-=+-+=++=++abcb a ab abc b a b a abc c b a ab c ca b bc a 故选(D ).5、方程256323+-=++y y x x x 的整数解(x ,y )的个数是( )A 、0B 、1C 、3D 、无穷多 答案:A解析:原方程可化为()()()()()2113212++-=++++y y y x x x x x因为三个连续整数的乘积是3的倍数,所以上式左边是3的倍数,而右边除以3余2,这是不可能的。
2007—2014全国初中数学联赛试题汇编(含答案)

第二试 ( A)
一、 (本题满分 20 分)设 m, n 为正整数,且 m 2 ,如果对一切实数 t ,二次函数
y x 2 (3 mt) x 3mt 的图象与 x 轴的两个交点间的距离不小于 2t n ,求 m, n 的值.
解 因为一元二次方程 x (3 mt ) x 3mt 0 的两根分别为 mt 和 3 ,所以二次函
y 6, z 4 .
因此,共有 1+2+3+4=10 种可能的摸球结果,其中摸出的球中恰好有 3 个红球的结 果有 2 种,所以所求的概率为
2 1 . 故选(B). 10 5
二、填空题(本题满分 28 分,每小题 7 分) 1. 设 x
1 2 1 1
,a 是 x 的小数部分,b 是 x 的小数部分, 则 a 3 b 3 3ab ____1___.
注:本题也可用特殊值法来判断.
2.当 x 分别取值
1 1 1 1 , , ,…, ,1 ,2 ,…, 2005 ,2006 , 2007 时, 2007 2006 2005 2
的 值 , 将 所 得 的 结 果 相 加 , 其 和 等 于
1 x2 计 算 代 数 式 1 x2
( ) (A)-1. 【答】C.
3 3
2. 对于一切不小于 2 的自然数 n , 关于 x 的一元二次方程 x (n 2) x 2n 0 的两个根
2 2
记作 a n , bn( n 2 ) , 则
1 1 1 = (a 2007 2)(b2007 2) (a 2 2)(b2 2) (a3 2)(b3 2)
2007 年全国初中数学联合竞赛
第一试
一、选择题(本题满分 42 分,每小题 7 分) 1. 已知 x, y, z 满足
2007年“数学周报杯”全国初中数学竞赛试卷及试卷解析

2007年“数学周报杯”全国初中数学竞赛试卷一、选择题(共5小题,每小6分,满分30分)1.(6分)方程组的解的个数为()A.1B.2C.3D.42.(6分)口袋中有20个球,其中白球9个,红球5个,黑球6个.现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数是()A.20B.18C.16D.143.(6分)已知△ABC为锐角三角形,⊙O经过点B,C,且与边AB,AC分别相交于点D,E.若⊙O的半径与△ADE的外接圆的半径相等,则⊙O一定经过△ABC的()A.内心B.外心C.重心D.垂心4.(6分)已知三个关于x的一元二次方程ax2+bx+c=0,bx2+cx+a=0,cx2+ax+b=0恰有一个公共实数根,则的值为()A.0B.1C.2D.35.(6分)方程x3+6x2+5x=y3﹣y+2的整数解(x,y)的个数是()A.0B.1C.3D.无穷多二、填空题(共5小题,每小题6分,满分30分)6.(6分)如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC 的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是.7.(6分)如图,点A,C都在函数的图象上,点B,D都x轴上,且使得△OAB,△BCD都是等边三角形,则点D的坐标为.8.(6分)已知点A,B的坐标分别为(1,0),(2,0).若二次函数y=x2+(a ﹣3)x+3的图象与线段AB只有一个交点,则a的取值范围是.9.(6分)如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=n•90°,则n=.10.(6分)已知对于任意正整数n,都有a1+a2+…+a n=n3,则=.三、解答题(共8小题,满分60分)11.(15分)已知点M,N的坐标分别为(0,1),(0,﹣1),点P是抛物线y= x2上的一个动点.(1)求证:以点P为圆心,PM为半径的圆与直线y=﹣1的相切;(2)设直线PM与抛物线y=x2的另一个交点为点Q,连接NP,NQ,求证:∠PNM=∠QNM.12.(15分)已知a,b都是正整数,试问关于x的方程是否有两个整数解?如果有,请把它们求出来;如果没有,请给出证明.13.(15分)已知AB为半圆O的直径,点P为直径AB上的任意一点.以点A 为圆心,AP为半径作⊙A,⊙A与半圆O相交于点C;以点B为圆心,BP为半径作⊙B,⊙B与半圆O相交于点D,且线段CD的中点为M.求证:MP 分别与⊙A和⊙B相切.14.(15分)(1)是否存在正整数m,n,使得m(m+2)=n(n+1)?(2)设k(k≥3)是给定的正整数,是否存在正整数m,n,使得m(m+k)=n (n+1)?15.已知抛物线y=﹣x2﹣3x+4和抛物线y=x2﹣3x﹣4相交于A,B两点.点P在抛物线C1上,且位于点A和点B之间;点Q在抛物线C2上,也位于点A和点B之间.(1)求线段AB的长;(2)当PQ∥y轴时,求PQ长度的最大值.16.实数a,b,c满足a≤b≤c,且ab+bc+ca=0,abc=1.求最大的实数k,使得不等式|a+b|≥k|c|恒成立.17.如图,点E,F分别在四边形ABCD的边AD,BC的延长线上,且满足.若CD,FE的延长线相交于点G,△DEG的外接圆与△CFG的外接圆的另一个交点为点P,连接PA,PB,PC,PD.求证:(1);(2)△PAB∽△PDC.18.证明:对任意三角形,一定存在两条边,它们的长u,v满足1≤.2007年“数学周报杯”全国初中数学竞赛试卷参考答案与试题解析一、选择题(共5小题,每小6分,满分30分)1.(6分)方程组的解的个数为()A.1B.2C.3D.4【分析】由于x、y的符号不确定,因此本题要分情况讨论.【解答】解:当x≥0,y≤0时,原方程组可化为:,解得;由于y≤0,所以此种情况不成立.当x≤0,y≥0时,原方程组可化为:,解得.当x≥0,y≥0时,,无解;当x≤0,y≤0时,,无解;因此原方程组的解为:.故选:A.【点评】在解含有绝对值的二元一次方程组时,要分类讨论,不可漏解.2.(6分)口袋中有20个球,其中白球9个,红球5个,黑球6个.现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数是()A.20B.18C.16D.14【分析】根据题意,则白球有7种取法:2、3、4、5、6、7、8;红球有4种取法:2、3、4、5,黑球有4种取法:0、1、2、3.然后根据所取球的总数为10,用枚举法,将所有可能的情况列举出来,然后再计算一共有多少种取法.【解答】解:用枚举法:因此所求的种数一共有4+4+4+4=16种.故选:C.【点评】此题首先要分析出各种球有多少种取法,再结合总数分析搭配的方法.3.(6分)已知△ABC为锐角三角形,⊙O经过点B,C,且与边AB,AC分别相交于点D,E.若⊙O的半径与△ADE的外接圆的半径相等,则⊙O一定经过△ABC的()A.内心B.外心C.重心D.垂心【分析】连接BE.根据两个圆的半径相等和圆周角定理可以证明∠BAC=∠ABE,再结合三角形的外角的性质可以证明∠BEC=2∠BAC,从而肯定该圆一定过三角形的外心.【解答】解:如图,连接BE.∵△ABC为锐角三角形,∴∠BAC,∠ABE均为锐角.∵⊙O的半径与△ADE的外接圆的半径相等,且DE为两圆的公共弦,∴∠BAC=∠ABE.∴∠BEC=∠BAC+∠ABE=2∠BAC.若△ABC的外心为O1,则∠BO1C=2∠BAC,∴⊙O一定过△ABC的外心.故选:B.【点评】此题综合运用了圆周角定理、三角形的外角的性质.4.(6分)已知三个关于x的一元二次方程ax2+bx+c=0,bx2+cx+a=0,cx2+ax+b=0恰有一个公共实数根,则的值为()A.0B.1C.2D.3【分析】设三个方程的公共根为x0,代入三个方程得到a,b,c的关系,然后代入代数式求出代数式的值.【解答】解:x0是它们的一个公共实数根,则ax02+bx0+c=0,bx02+cx0+a=0,cx02+ax0+b=0.把上面三个式子相加,并整理得(a+b+c)(x02+x0+1)=0.因为,所以a+b+c=0.于是=故选:D.【点评】本题考查的是一元二次方程的公共解,一般是设公共解,代入方程,确定a,b,c的值,然后求出代数式的值.5.(6分)方程x3+6x2+5x=y3﹣y+2的整数解(x,y)的个数是()A.0B.1C.3D.无穷多【分析】先把方程左边化为3的倍数的形式,再根据方程右边不可能是3的倍数判断出方程无整数解即可.【解答】解:原方程可化为x(x+1)(x+2)+3(x2+x)=y(y﹣1)(y+1)+2,∵三个连续整数的乘积是3的倍数,∴上式左边是3的倍数,而右边除以3余2,这是不可能的.∴原方程无整数解.故选:A.【点评】本题考查的是非一次不定方程的解,熟知三个连续整数的乘积是3的倍数是解答此题的关键.二、填空题(共5小题,每小题6分,满分30分)6.(6分)如图,在直角三角形ABC中,∠ACB=90°,CA=4,点P是半圆弧AC 的中点,连接BP,线段即把图形APCB(指半圆和三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是4.【分析】连接OP、OB,把两部分的面积均可转化为规则图形的面积,不难发现两部分面积之差的绝对值即为三角形BOP的面积的2倍.【解答】解:连接OP、OB,∵图形BAP的面积=△AOB的面积+△BOP的面积+扇形OAP的面积,图形BCP的面积=△BOC的面积+扇形OCP的面积﹣△BOP的面积,又∵点P是半圆弧AC的中点,OA=OC,∴扇形OAP的面积=扇形OCP的面积,△AOB的面积=△BOC的面积,=OP•OC=4.∴两部分面积之差的绝对值是2S△BOP【点评】此题要能够把不规则图形的面积转化为规则图形的面积.注意根据已知条件发现面积相等的图形.7.(6分)如图,点A,C都在函数的图象上,点B,D都x轴上,且使得△OAB,△BCD都是等边三角形,则点D的坐标为(2,0).【分析】设△OAB,△BCD边长的一半为a,b,根据等边三角形的性质可得点A的纵坐标,点C的纵坐标,代入反比例函数解析式可得两个等边三角形边长的一半,相加后乘2即为点D的横坐标,点D在x轴上,所以纵坐标为0.【解答】解:如图,分别过点A,C作x轴的垂线,垂足分别为E,F.设OE=a,BF=b,则AE=a,CF=,∴点A,C的坐标为,(a,),(2a+b,),∴,解得,∴点D的坐标为(,0).【点评】综合考查等边三角形和反比例函数的性质;得到用等边三角形边长的一半表示点A和点C的坐标是解决本题的突破点.8.(6分)已知点A,B的坐标分别为(1,0),(2,0).若二次函数y=x2+(a ﹣3)x+3的图象与线段AB只有一个交点,则a的取值范围是﹣1≤a<﹣或a=3﹣2.【分析】根据题意,当二次函数顶点在x轴下方或当二次函数的顶点在x轴上时,分情况讨论问题.借助于根的判别式即可解答.【解答】解:依题意,应分为两种情况讨论,①当二次函数顶点在x轴下方,若y x=1<0且y x=2≥0,即,解得此不等式组无解;若y x=2<0且y x=1≥0,即,解得﹣1≤a<﹣;②当二次函数的顶点在x轴上时,△=0,即(a﹣3)2﹣12=0,解得a=3±2,而对称轴为x=﹣,可知1≤﹣≤2,故a=3﹣2.故答案为:﹣1≤a<﹣或a=3﹣2.【点评】此题是二次函数综合题,主要考查了二次函数对称轴的确定方法,一元二次方程的根的判别式,用分类讨论的数学思想,是解本题的关键.9.(6分)如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=n•90°,则n=6.【分析】连接BE,根据三角形内角与外角的性质可得,∠1=∠A+∠D,∠1+∠G=∠2,再根据四边形及三角形内角和定理解答即可.【解答】解:连接BE,GE.∵∠1是△ADH的外角,∴∠1=∠A+∠D,∵∠2是△JHG的外角,∴∠1+∠G=∠2,∴在四边形BEFJ中,∠EBJ+∠BJF+∠EFJ+∠BEF=360°…①,在△BCE中,∠EBC+∠C+∠BEC=180°…②,①+②得,∠BEG+∠BGF+∠F+∠BEF+∠EBC+∠C+∠BEC=360°+180°=540°,即∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°,∴n==6.∴n=6.故答案为:6.【点评】此题比较复杂,解答此题的关键是作出辅助线,利用三角形内角与外角的关系把所求的角的度数归结到三角形或四边形中,利用三角形和四边形的内角和定理解答.10.(6分)已知对于任意正整数n,都有a1+a2+…+a n=n3,则=.【分析】先根据n≥2时,a1+a2+…+a n+a n=n3,a1+a2+…+a n﹣1=(n﹣1)3,把两式﹣1相减,得出a n的表达式,再根据=(﹣)进行解答即可.【解答】解:∵当n≥2时,有a1+a2+…+a n+a n=n3,a1+a2+…+a n﹣1=(n﹣1)3,﹣1两式相减,得a n=3n2﹣3n+1,∴==(﹣),∴++…+,=(1﹣)+(﹣)+…+(﹣),=(1﹣),=.故答案为:.【点评】本题考查的是部分分式,属规律性题目,能根据题意得出=(﹣)是解答此题的关键.三、解答题(共8小题,满分60分)11.(15分)已知点M,N的坐标分别为(0,1),(0,﹣1),点P是抛物线y= x2上的一个动点.(1)求证:以点P为圆心,PM为半径的圆与直线y=﹣1的相切;(2)设直线PM与抛物线y=x2的另一个交点为点Q,连接NP,NQ,求证:∠PNM=∠QNM.【分析】(1)可先根据抛物线的解析式设出P点的坐标,那么可得出PM的长的表达式,P点到y=﹣1的长就是P点的纵坐标与﹣1的差的绝对值,那么可判断得出的表示PM和P到y=﹣1的距离的两个式子是否相等,如果相等,则y=﹣1是圆P的切线.(2)可通过构建相似三角形来求解,过Q,P作QR⊥直线y=﹣1,PH⊥直线y=﹣1,垂足为R,H,那么QR∥MN∥PH,根据平行线分线段成比例定理可得出QM:MP=RN:NH.(1)中已得出了PM=PH,那么同理可得出QM=QR,那么比例关系式可写成QR:PH=RN:NH,而这两组对应成比例的线段的夹角又都是直角,因此可求出∠QNR=∠PNH,根据等角的余角相等,可得出∠QNM=∠PNM.【解答】解:(1)设点P的坐标为(x0,x20),则PM==x20+1;又因为点P到直线y=﹣1的距离为,x20﹣(﹣1)=x20+1所以,以点P为圆心,PM为半径的圆与直线y=﹣1相切.(2)如图,分别过点P,Q作直线y=﹣1的垂线,垂足分别为H,R.由(1)知,PH=PM,同理可得,QM=QR.因为PH,MN,QR都垂直于直线y=﹣1,所以,PH∥MN∥QR,于是=,所以,因此,Rt△PHN∽Rt△QRN.于是∠HNP=∠RNQ,从而∠PNM=∠QNM.【点评】本题主要考查了相似三角形的性质,平行的性质以及二次函数和一次函数的综合应用.(2)中通过构建相似三角形来求角相等是解题的关键.12.(15分)已知a,b都是正整数,试问关于x的方程是否有两个整数解?如果有,请把它们求出来;如果没有,请给出证明.【分析】不妨设a≤b,且方程的两个整数根为x1,x2(x1≤x2),而a,b都是正整数,根据根与系数的关系得到x1+x2=ab>0,x1x2=(a+b)>0,则如果原方程存在两整数根,则两根必为正整数.当a,b 中至少有一个等于1时,a+b ≥ab;不妨设a=1,此时有(a+b)=(1+b)≤b=ab (当且仅当b=1时等号成立),其余情况下都有(a+b)<a+b≤ab;则有(x1﹣1)(x2﹣1)≤1,得到x1=1,x2=(a+b),则(a﹣1)(b﹣1)=3﹣ab,根据整数的性质得到a=1,b=3,或a=3,b=1.即得到x2=2.【解答】解:关于x的方程有两个整数解.不妨设a≤b,且方程的两个整数根为x1,x2(x1≤x2),而a,b都是正整数,∴x1+x2=ab>0,x1x2=(a+b)>0,∴如果原方程存在两整数根,则两根必为正整数.当a,b 中至少有一个等于1时,a+b≥ab;不妨设a=1,此时有(a+b)=(1+b)≤b=ab (当且仅当b=1时等号成立),其余情况下都有(a+b)<a+b≤ab;∴x1x2≤x1+x2,∴x1x2﹣x1﹣x2+1≤1,∴(x1﹣1)(x2﹣1)≤1,∴x1=1,∴x2=(a+b),∴1+(a+b)=ab,即2+a+b=2ab,∴(a﹣1)(b﹣1)=3﹣ab,而a,b都是正整数,∴3﹣ab≥0,所以a=1,b=3,或a=3,b=1.∴x2=2,∴a=1,b=3,一元二次方程为x2﹣3x+2=0,它的两个根为x1=1,x2=2.【点评】本题考查了求一元二次方程的整数根的方法:利用根与系数的关系消去未知系数,得到两整数根的关系,然后利用整数的性质求出两整数根.13.(15分)已知AB为半圆O的直径,点P为直径AB上的任意一点.以点A 为圆心,AP为半径作⊙A,⊙A与半圆O相交于点C;以点B为圆心,BP为半径作⊙B,⊙B与半圆O相交于点D,且线段CD的中点为M.求证:MP 分别与⊙A和⊙B相切.【分析】要证MP分别与⊙A和⊙B相切,如图示,连接AC,AD,BC,BD,并且分别过点C,D作CE⊥AB,DF⊥AB,垂足分别为E,F则CE∥DF.因为AB 是⊙O的直径,所以∠ACB=∠ADB=90°.在Rt△ABC和Rt△ABD中,由射影定理得PA2=AC2=AE•AB,PB2=BD2=BF•AB.两式相减可得PA2﹣PB2=AB(AE﹣BF),又PA2﹣PB2=(PA+PB)(PA﹣PB)=AB(PA﹣PB),于是有AE﹣BF=PA﹣PB,即PA﹣AE=PB﹣BF,所以PE=PF,也就是说,点P是线段EF的中点.因此,MP 是直角梯形CDEF的中位线,于是得MP⊥AB,进而可得MP分别与⊙A和⊙B 相切.【解答】证明:如图,连接AC,AD,BC,BD,并且分别过点C,D作CE⊥AB,DF⊥AB,垂足分别为E,F∴CE∥DF,∠AEC=90°,∠BFD=90°.∵AB是⊙O的直径,∴∠ACB=∠ADB=90°.又∵∠CAB是△ACB和△AEC的公共角,∴△ACB∽△AEC,∴AC:AB=AE:AC即PA2=AC2=AE•AB,同理PB2=BD2=BF•AB.两式相减可得PA2﹣PB2=AB(AE﹣BF),∴PA2﹣PB2=(PA+PB)(PA﹣PB)=AB(PA﹣PB),∴AE﹣BF=PA﹣PB,即PA﹣AE=PB﹣BF,∴PE=PF,∴点P是线段EF的中点.∵M是CD的中点,∴MP是直角梯形CDEF的中位线,∴MP⊥AB,∴MP分别与⊙A和⊙B相切.【点评】这道题考查了相切两圆的性质和射影定理的应用,以及中位线的知识,同学们应熟练掌握.14.(15分)(1)是否存在正整数m,n,使得m(m+2)=n(n+1)?(2)设k(k≥3)是给定的正整数,是否存在正整数m,n,使得m(m+k)=n (n+1)?【分析】(1)m(m+2)=n(n+1)可以变化成(m+1)2=n2+n+1,若存在,则n2+n+1即是一个平方数,即可判断;(2)当k=3时,利用与(1)相同的方法即可证明;当k≥4时,可以分k是偶数与奇数两种情况进行讨论,当k是偶数时,可以设k=2t(t是不小于2的整数),代入式子进行讨论;当k是奇数时,可以设k=t+1(t是不小于2的整数),代入即可判断.【解答】解:(1)答案是否定的.若存在正整数m,n,使得m(m+2)=n(n+1),则(m+1)2=n2+n+1,显然n>1,于是n2<n2+n+1<(n+1)2,所以,n2+n+1不是平方数,矛盾.(5分)(2)当k=3时,若存在正整数m,n,满足m(m+3)=n(n+1),则4m2+12m=4n2+4n,(2m+3)2=(2n+1)2+8,(2m+3﹣2n﹣1)(2m+3+2n+1)=8,(m﹣n+1)(m+n+2)=2,而m+n+2>2,故上式不可能成立.(10分)当k≥4时,若k=2t(t是不小于2的整数)为偶数,取m=t2﹣t,n=t2﹣1则m (m+k)=(t2﹣t)(t2+t)=t4﹣t2,n(n+1)=(t2﹣1)t2=t4﹣t2,因此这样的(m,n)满足条件.若k=2t+1(t是不小于2的整数)为奇数,取m=,n=则m(m+k)=(+2t+1)=(t4+2t3﹣t2﹣2t),n(n+1)==(t4+2t3﹣t2﹣2t),因此这样的(m,n)满足条件.综上所述,当k=3时,答案是否定的;当k≥4时,答案是肯定的.(15分)【点评】本题主要考查了整数的奇偶性,正确对k的范围进行分类,根据k的奇偶性对已知的式子m(m+k)=n(n+1)进行变形是解题的关键.15.已知抛物线y=﹣x2﹣3x+4和抛物线y=x2﹣3x﹣4相交于A,B两点.点P在抛物线C1上,且位于点A和点B之间;点Q在抛物线C2上,也位于点A和点B之间.(1)求线段AB的长;(2)当PQ∥y轴时,求PQ长度的最大值.【分析】(1)根据抛物线y=﹣x2﹣3x+4和抛物线y=x2﹣3x﹣4相交于A,B两点,联立解方程组求得x、y的值,进而确定A、B的坐标.通过直角坐标系中两点间的距离公式求得AB的长.(2)由(1)可知P点的横坐标取值介于A、B之间.当PQ∥y轴时,说明P、Q两点的横坐标相同,只要作纵坐标的差的绝对值,根据横坐标的取值,确定差的最大值即可.【解答】解:(1)由题意得,解方程组得,;∴点A,B的坐标分别是(﹣2,6),(2,﹣6).于是AB=.(2)如图,当PQ∥y轴时,设点P,Q的坐标分别为(t,﹣t2﹣3t+4),(t,t2﹣3t﹣4),﹣2<t<2,因此PQ=2(4﹣t2)≤8,当t=0时等号成立,所以,PQ的长的最大值为8.答:(1)线段AB的长为;(2)PQ长度的最大值为8.【点评】本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点.主要考查学生数形结合的数学思想方法.16.实数a,b,c满足a≤b≤c,且ab+bc+ca=0,abc=1.求最大的实数k,使得不等式|a+b|≥k|c|恒成立.【分析】通过实数a,b,c满足a≤b≤c,且ab+bc+ca=0,abc=1,利用c表示a+b和ab,并且确定它们的符号.然后写出以a、b为根的一元二次方程,则有△≥0,得到c的范围,再变形|a+b|,有|a+b|=﹣(a+b)=≥4c=4|c|,最后确定k的范围,找到k的最大值.【解答】解:不等式|a+b|≥4|c|对满足题设条件的实数a,b,c恒成立.由已知条件知,a,b,c都不等于0,且c>0.因为abc=1,有ab=>0;又因为ab+bc+ca=0,所以a+b=﹣<0,所以a≤b<0.由一元二次方程根与系数的关系知,a,b是一元二次方程x2+x+=0的两个实数根,于是△=﹣≥0,所以c3≤.因此|a+b|=﹣(a+b)=≥4c=4|c|,不等式|a+b|≥4|c|对满足题设条件的实数a,b,c恒成立,所以k≤4,最大的实数k为4.【点评】本题考查了一元二次方程根的判别式.当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.也考查了一元二次方程根与系数的关系,以a,b两数为根的方程为:x2+(a+b)x+ab=0.熟练掌握不等式的性质和绝对值的含义.17.如图,点E,F分别在四边形ABCD的边AD,BC的延长线上,且满足.若CD,FE的延长线相交于点G,△DEG的外接圆与△CFG的外接圆的另一个交点为点P,连接PA,PB,PC,PD.求证:(1);(2)△PAB∽△PDC.【分析】(1)接PE,PF,PG,可得△PDC∽△PEF,△PDE∽△PCF,得出对应线段成比例,再通过转化即可得出结论;(2)由(1)中的三角形相似可得,∠DPA=∠CPB,得出∠APB=∠DPC,即可得出三角形相似.【解答】证明:(1)连接PE,PF,PG,∵∠PDG=∠PEG,∴∠PDC=∠PEF.又∵∠PCG=∠PFG,∴△PDC∽△PEF,即,∠CPD=∠FPE从而△PDE∽△PCF,∴=.又∵=,∴=;(2)由于∠PDA=∠PGE=∠PCB,结合(1)知,△PDA∽△PCB,从而有,∠DPA=∠CPB,∴∠APB=∠DPC,∴△PAB∽△PDC.【点评】本题主要考查了相似三角形的判定及性质问题,题中涉及一部分圆的有关知识,能够熟练掌握.18.证明:对任意三角形,一定存在两条边,它们的长u,v满足1≤.【分析】设任意△ABC的三边长为a,b,c,不妨设a>b>c.若结论不成立,则可证明和的取值范围,然后记b=c+s,a=b+t=c+s+t,求得和的取值范围,再令x=,y=,根据条件证明y<1.【解答】证明:设任意△ABC的三边长为a,b,c,不妨设a>b>c.若结论不成立,则必有①≥.②记b=c+s,a=b+t=c+s+t,显然s,t>0代入得≥,≥,令x=,y=则≥.③由a<b<c,得c+s+t<c+s+c,即t<c,于是.y=<1由②得=1+x≥,④由③,④得y≥(﹣1)(1+x)≥=1,此式与y<1矛盾.从而命题得证.【点评】本题主要考查抽屉原理的知识点,根据假设法证明是解答本题的关键,本题难度较大.。
全国初中数学竞赛试题参考答案
中国教育学会中学数学教学专业委员会“《数学周报》杯”2007年全国初中数学竞赛试题参考答案一、选择题(共5小题,每小题6分,满分30分. 以下每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填得零分)1.方程组12,6x y x y ⎧+=⎪⎨+=⎪⎩的解的个数为( ).(A )1 (B ) 2 (C ) 3 (D )4答:(A ).解:若x ≥0,则12,6,x y x y +=⎧⎪⎨+=⎪⎩于是6y y -=-,显然不可能. 若0x <,则 12,6,x y x y -+=⎧⎪⎨+=⎪⎩于是18y y +=,解得9y =,进而求得3x =-.所以,原方程组的解为⎩⎨⎧=-=,9,3y x 只有1个解.故选(A ).2.口袋中有20个球,其中白球9个,红球5个,黑球6个.现从中任取10个球,使得白球不少于2个但不多于8个,红球不少于2个,黑球不多于3个,那么上述取法的种数是( ).(A ) 14 (B ) 16 (C )18 (D )20 答:(B ).解:用枚举法:红球个数 白球个数 黑球个数 种 数 5 2,3,4,5 3,2,1,0 4 4 3,4,5,6 3,2,1,0 4 3 4,5,6,7 3,2,1,0 4 2 5,6,7,8 3,2,1,0 4 所以,共16种.故选(B ).3.已知△ABC 为锐角三角形,⊙O 经过点B ,C ,且与边AB ,AC 分别相交于点D ,E . 若⊙O 的半径与△ADE 的外接圆的半径相等,则⊙O 一定经过△ABC 的( ).(A )内心 (B )外心 (C )重心 (D )垂心答:(B ).解: 如图,连接BE ,因为△ABC 为锐角三角形,所以BAC ∠,ABE ∠均为锐角.又因为⊙O 的半径与△ADE 的外接圆的半径相等,且DE 为两圆的公共弦,所以BAC ABE ∠=∠.于是,2BEC BAC ABE BAC ∠=∠+∠=∠.若△ABC 的外心为1O ,则12B OC B A C ∠=∠,所以,⊙O 一定过△ABC 的外心.故选(B ).4.已知三个关于x 的一元二次方程 02=++c bx ax ,02=++a cx bx ,02=++b ax cx 恰有一个公共实数根,则222a b c bc ca ab++的值为( ). (A ) 0 (B )1 (C )2 (D )3答:(D ).解:设0x 是它们的一个公共实数根,则0020=++c bx ax ,0020=++a cx bx ,0020=++b ax cx .把上面三个式子相加,并整理得200()(1)0a b c x x ++++=. 因为22000131()024x x x ++=++>,所以0a b c ++=. 于是222333333()a b c a b c a b a b bc ca ab abc abc+++-+++== 3()3ab a b abc-+==. 故选(D ).5.方程323652x x x y y ++=-+的整数解(x ,y )的个数是( ).(A )0 (B )1 (C )3 (D )无穷多答:(A ).解:原方程可化为2(1)(2)3(1)(1)2x x x x x y y y ++++=-++(),因为三个连续整数的乘积是3的倍数,所以上式左边是3的倍数,而右边除以3余2,这是不可能的.所以,原方程无整数解.故选(A).二、填空题(共5小题,每小题6分,满分30分)6.如图,在直角三角形ABC 中,90ACB ∠=︒,CA =4.点P 是半圆弧AC 的中点,连接BP ,线段BP 把图形APCB 分成两部分,则这两部分面积之差的绝对值是 .答:4.解:如图,设AC 与BP 相交于点D ,点D 关于圆心O 的对称点记为点E ,线段BP 把图形APCB 分成两部分,这两部分面积之差的绝对值是△BEP 的面积,即△BOP 面积的两倍.而1122222BPO S PO CO ∆=⋅=⨯⨯=. 因此,这两部分面积之差的绝对值是4.7.如图, 点A ,C都在函数0)y x =>的图象上,点B ,D 都在x 轴上,且使得△OAB ,△BCD 都是等边三角形,则点D 的坐标为 .答:(0).解:如图,分别过点A ,C 作x 轴的垂线,垂足分别为E ,F .设OE =a ,BF =b , 则AE,CF,所以,点A ,C 的坐标为(a),(2a +b),所以2(2)a b =+= 解得a b ⎧=⎪⎨=⎪⎩ 因此,点D的坐标为(0).8.已知点A ,B 的坐标分别为(1,0),(2,0). 若二次函数()233y x a x =+-+的图象与线段AB 恰有一个交点,则a 的取值范围是 .答:1-≤12a <-,或者3a =- 解:分两种情况:(Ⅰ)因为二次函数()233y x a x =+-+的图象与线段AB 只有一个交点,且点A ,B 的坐标分别为(1,0),(2,0),所以[][]032)3(231)3(122<+⨯-+⨯+⨯-+a a , 得112a -<<-. 由031)3(12=+⨯-+a ,得1a =-,此时11=x ,32=x ,符合题意;由032)3(22=+⨯-+a ,得12a =-,此时21=x ,232=x ,不符合题意. (Ⅱ)令()2330x a x +-+=,由判别式0∆=,得3a =±当3a =+时,12x x ==不合题意;当3a =-12x x ==符合题意.综上所述,a 的取值范围是1-≤12a <-,或者3a =- 9.如图,90A B C D E F G n ∠+∠+∠+∠+∠+∠+∠=⋅︒,则n = . 答:6.解:如图,设AF 与BG 相交于点Q ,则AQG A D G ∠=∠+∠+∠,于是A B C D E F G ∠+∠+∠+∠+∠+∠+∠B C E F AQG =∠+∠+∠+∠+∠B C E F BQF =∠+∠+∠+∠+∠540690=︒=⨯︒.所以,n =6.10.已知对于任意正整数n ,都有 312n a a a n +++=, 则 23100111111a a a +++=---.答:33100. 解:当n ≥2时,有 3121n a a a a n n =++++- ,3121(1)n a a a n -+++=-,两式相减,得 2331n a n n =-+, 所以 ),111(31)1(3111nn n n a n --=-=- ,4,3,2=n 因此 23100111111a a a +++--- 11111111(1)()()32323399100=-+-++- 1133(1)3100100=-=. 三、解答题(共4题,每小题15分,满分60分)11(A ).已知点M ,N 的坐标分别为(0,1),(0,-1),点P 是抛物线214y x =上的一个动点.(1)判断以点P 为圆心,PM 为半径的圆与直线1y =-的位置关系;(2)设直线PM 与抛物线214y x =的另一个交点为点Q ,连接NP ,NQ ,求证:PNM QNM ∠=∠.解:(1)设点P 的坐标为2001(,)4x x ,则 PM =20114x ==+; 又因为点P 到直线1y =-的距离为220011(1)144x x --=+, 所以,以点P 为圆心,PM 为半径的圆与直线1y =-相切.…………5分(2)如图,分别过点P ,Q 作直线1y =-的垂线,垂足分别为H ,R .由(1)知,PH =PM ,同理可得,QM=QR .因为PH ,MN ,QR 都垂直于直线1y =-,所以,PH ∥MN ∥QR ,于是 QM MP RNNH =, 所以 Q R P H R N H N=, 因此,Rt △PHN ∽Rt △QRN .于是HNP RNQ ∠=∠,从而PNM QNM ∠=∠.…………15分12(A ).已知a ,b 都是正整数,试问关于x 的方程21()02x abx a b -++=是 否有两个整数解?如果有,请把它们求出来;如果没有,请给出证明.解:不妨设a ≤b ,且方程的两个整数根为12,x x (1x ≤2x ),则有1212,1(),2x x ab x x a b +=⎧⎪⎨=+⎪⎩所以 12121122x x x x a b ab --=+-,124(1)(1)(21)(21)5x x a b --+--=. …………5分因为a ,b 都是正整数,所以x 1,x 2均是正整数,于是,11x -≥0,21x -≥0,21a -≥1,21b -≥1,所以12(1)(1)0,(21)(21)5,x x a b --=⎧⎨--=⎩ 或 ⎩⎨⎧=--=--.1)12)(12(,1)1)(121b a x x ( (1)当12(1)(1)0,(21)(21)5x x a b --=⎧⎨--=⎩时,由于a ,b 都是正整数,且a ≤b ,可得 a =1,b =3,此时,一元二次方程为2320x x -+=,它的两个根为11x =,22x =.(2)当12(1)(1)1,(21)(21)1x x a b --=⎧⎨--=⎩时,可得 a =1,b =1,此时,一元二次方程为210x x -+=,它无整数解.综上所述,当且仅当a =1,b =3时,题设方程有整数解,且它的两个整数解为11x =,22x =. ……………15分13(A ).已知AB 为半圆O 的直径,点P 为直径AB上的任意一点.以点A 为圆心,AP 为半径作⊙A ,⊙A 与半圆O 相交于点C ;以点B 为圆心,BP 为半径作⊙B ,⊙B 与半圆O 相交于点D ,且线段CD 的中点为M .求证:MP 分别与⊙A 和⊙B 相切.证明:如图,连接AC ,AD ,BC ,BD ,并且分别过点C ,D 作AB 的垂线,垂足分别为,EF ,则CE ∥DF .因为AB 是⊙O 的直径,所以90ACB ADB ∠=∠=︒.在Rt △ABC 和Rt △ABD 中,由射影定理得22PA AC AE AB ==⋅,22PB BD BF AB ==⋅. ……………5分两式相减可得()22PA PB AB AE BF -=-,又 ()22()()PA PB PA PB PA PB AB PA PB -=+-=-, 于是有 AE BF PA PB -=-,即 PA AE PB BF -=-,所以PE PF =,也就是说,点P 是线段EF 的中点.因此,MP 是直角梯形CDFE 的中位线,于是有MP AB ⊥,从而可得MP 分别与⊙A 和⊙B 相切.……………15分14(A ).(1)是否存在正整数m ,n ,使得(2)(1)m m n n +=+?(2)设k (k ≥3)是给定的正整数,是否存在正整数m ,n ,使得()(1)m m k n n +=+?解:(1)答案是否定的.若存在正整数m ,n ,使得(2)(1)m m n n +=+,则22(1)1m n n +=++,显然1n >,于是2221(1)n n n n <++<+,所以,21n n ++不是平方数,矛盾. ……………5分(2)当3k =时,若存在正整数m ,n ,满足(3)(1)m m n n +=+,则2241244m m n n +=+,22(23)(21)8m n +=++,(2321)(2321)8m n m n +--+++=,(1)(2)2m n m n -+++=,而22m n ++>,故上式不可能成立.………………10分当k ≥4时,若2k t =(t 是不小于2的整数)为偶数,取22,1m t t n t =-=-,则 2242()()()m m k t t t t t t +=-+=-, 2242(1)(1)n n t t t t +=-=-,因此这样的(m ,n )满足条件.若2k t =+1(t 是不小于2的整数)为奇数,取222,22t t t t m n -+-==, 则 224321()(21)(22)224t t t t m m k t t t t t --+=++=+--, 2243221(1)(22)224t t t t n n t t t t +-++=⋅=+--, 因此这样的(m ,n )满足条件.综上所述,当3k =时,答案是否定的;当k ≥4时,答案是肯定的.……………15分 注:当k ≥4时,构造的例子不是唯一的.11(B ).已知抛物线1C :234y x x =--+和抛物线2C :234y x x =--相交 于A ,B 两点. 点P 在抛物线1C 上,且位于点A 和点B 之间;点Q 在抛物线2C 上,也位于点A 和点B 之间.(1)求线段AB 的长;(2)当PQ ∥y 轴时,求PQ 长度的最大值.解:(1)解方程组2234,34,y x x y x x ⎧=--+⎪⎨=--⎪⎩ 得 112,6,x y =-⎧⎨=⎩ 222,6,x y =⎧⎨=-⎩所以,点A ,B 的坐标分别是(-2,6),(2,-6).于是AB ==.…………5分(2)如图,当PQ ∥y 轴时,设点P ,Q 的坐标分别为)43,(2+--t t t , )43,(2--t t t , 22t -<<,因此 PQ 22(4)t =-≤8,当0t =时等号成立,所以,PQ 的长的最大值8.……………15分12(B ).实数a ,b ,c 满足a ≤b ≤c ,且0ab bc ca ++=,abc =1.求最大的实数k ,使得不等式a b +≥k c恒成立.解:当a b ==2c =时,实数a ,b ,c 满足题设条件,此时k ≤4. ……………5分 下面证明:不等式a b +≥4c 对满足题设条件的实数a ,b ,c 恒成立. 由已知条件知,a ,b ,c 都不等于0,且0c >.因为2110,0ab a b c c=>+=-<, 所以a ≤b 0<.由一元二次方程根与系数的关系知,a ,b 是一元二次方程22110x x c c++= 的两个实数根,于是414c c∆=-≥0, 所以 3c ≤14. ……………10分因此 21()a b a b c+=-+=≥44c c =. ……………15分13(B ).如图,点E ,F 分别在四边形ABCD 的边AD ,BC 的延长线上,且满足DE AD CF BC=.若CD ,FE 的延长线相交于点G ,△DEG 的外接圆与△CFG 的外接圆的另一个交点为点P ,连接P A ,PB ,PC ,PD .求证: (1)AD PD BC PC =; (2)△PAB ∽△PDC .证明:(1)连接PE ,PF ,PG ,因为PDG PEG ∠=∠,所以PDC PEF ∠=∠.又因为PCG PFG ∠=∠,所以△PDC ∽△PEF ,于是有 ,PD PE CPD FPE PC PF=∠=∠, 从而 △PDE ∽△PCF ,所以 PD DE PC CF=. 又已知DE AD CF BC =,所以,AD PD BC PC =. ………………10分(2)由于PDA PGE PCB ∠=∠=∠,结合(1)知,△PDA ∽△PCB ,从而有,PA PD PB PC= DPA CPB ∠=∠, 所以APB DPC ∠=∠,因此△PAB ∽△PDC . ………………15分14(B ).证明:对任意三角形,一定存在两条边,它们的长u ,v 满足1≤12u v +<证明:设任意△ABC 的三边长为a ,b ,c ,不妨设a b c >>.若结论不成立,则必有a b, ○1 b c≥12. ○2 ………………5分记,b c s a b t c s t =+=+=++,显然,0s t >,代入○1得c s t c s +++≥, 11s t c c s c+++, 令,s tx y c c==,则11x y x +++≥12+. ○3 由a b c <+,得c s t c s c ++<++,即t c <,于是1ty c=<. 由○2得1b c s x c c +==+, ○4 由○3,○4得y≥1(1)x ⎫+⎪⎪⎝⎭1=, 此式与1<y 矛盾.从而命题得证.………………15分2007年宁波市东海杯初二数学竞赛试卷第1试一、填空题(第1--20题每题3分,第21-30题每题4分,共100分)1.若实数a ,b ,c 满足abc=-2,a+b+c>O ,则a ,b ,c 中有 1 个负数.2.设a △b=a 2-2b ,则(-2)△(3△4)的值为 2 .3.如图,已知AB ∥CD ,MF ⊥FG ,∠AEM=50°,∠NHC=55°.则∠FGH 的度数为 15 .(第3题) (第4题)4.如图,把一个长26cm ,宽14cm 的长方形分成五块,其中两个大正方形和两个长方形分别全等.那么中间小正方形的面积是 36 cm 。
2007联赛答案
2007年全国初中数学联合竞赛试题参考答案及评分标准【答】B. 解 由x z z y x +=-=532得x z x y 23,3==,所以31333525=+-=+-x x x x z y y x ,故选(B ).注:本题也可用特殊值法来判断.【答】C.解 因为=+-++-222211)1(1)1(1n n nn 011112222=+-++-n n n n ,即当x分别取值n 1,n n (为正整数)时,计算所得的代数式的值之和为0;而当1=x 时,0111122=+-.因此,当x 分别取值20071,20061,20051,...,21,1,2, (2005)2006,2007时,计算所得各代数式的值之和为0.故选(C ).【答】D.解 由题意可得⎪⎪⎩⎪⎪⎨⎧-=----=---,5822,1)2(2b b a c b a b a c 即⎪⎩⎪⎨⎧==+,53,2b c a c b 所以b c 53=,b a 54=,因此222b c a =+,所以△ABC 是直角三角形. 故选(D ).【答】C.解 锐角△ABC 的垂心在三角形内部,如图,设△ABC 的外心为O ,D 为BC 的中点,BO 的延长线交⊙O 于点E ,连CE 、AE ,则CE //AH ,AE //CH ,则OD CE AH OB 2===,所以∠OBD =30°,∠BOD =60°,所以∠A =∠BOD =60°.故选(C ).【答】A.解 分别延长KD 、KE 、KF ,与△ABC 的三边AB 、BC 、CA 交于点M 、N 、P ,由于D 、E 、F 分别为△KAB 、△KBC 、△KCA 的重心,易知M 、N 、P 分别为AB 、BC 、CA 的中点,所以ABC MNP S S △△41=. 易证△DEF ∽△MNP ,且相似比为3:2,所以MNP DEF S S △△2)32(=ABC S △4194⋅=ABC S △91=. 所以:DEF S △19ABC S =△.故选(A ). 【答】B.解 设摸出的15个球中有x 个红球、y 个黑球、z 个白球,则z y x ,,都是正整数,且7,6,5≤≤≤z y x ,15=++z y x .因为13≤+z y ,所以x 可取值2,3,4,5.当2=x 时,只有一种可能,即7,6==z y ;当3=x 时,12=+z y ,有2种可能,7,5==z y 或6,6==z y ;当4=x 时,11=+z y ,有3种可能,7,4==z y 或6,5==z y 或5,6==z y ;AECB D O H当5=x 时,10=+z y ,有4种可能,7,3==z y 或6,4==z y 或5,5==z y 或4,6==z y .因此,共有1+2+3+4=10种可能的摸球结果,其中摸出的球中恰好有3个红球的结果有2种,所以所求的概率为51102=.故选(B ). 解 ∵12121+=-=x ,而3122<+<,∴122-=-=x a .又∵12--=-x ,而2123-<--<-,∴22)3(-=---=x b .∴1=+b a , ∴=++ab b a 333=++-+ab b ab a b a 3))((221)(3222=+=++-b a ab b ab a . 解 由根与系数的关系得2+=+n b a n n ,22n n a b n ⋅=-,所以=--)2)(2(n n b a (2-n n b a 4)++n n b a 222(2)42(1)n n n n =--++=-+,则11111()(2)(2)2(1)21n n a b n n n n =-=----++,)2)(2(122--b a )2)(2(133--+b a +)2)(2(120072007--+b a =11111111111003()()()()22334200720082220084016⎡⎤--+-++-=--=-⎢⎥⎣⎦. 解 延长CD 交⊙O 于点G ,设DG BE ,的中点分别为点N M ,,则易知DN AM =.因为10==CD BC ,由割线定理,易证DG BF =,所以42)(2)(2==-=-=-=-AB AM BM DN BM DG BE BF BE .解 设264100m a =+,264201n a =+,则100,32<≤n m ,两式相减得 ))((10122m n m n m n a -+=-=,因为101是质数,且101101<-<-m n ,所以101=+m n ,故1012-=-=n m n a .代入264201n a =+,整理得020*******=+-n n ,解得59=n ,或343=n (舍去).所以171012=-=n a .第二试 (A )解 因为一元二次方程03)3(2=--+mt x mt x 的两根分别为mt 和3-,所以二次函数mt x mt x y 3)3(2--+=的图象与x 轴的两个交点间的距离为3mt +.由题意,32mt t n +≥+,即22(3)(2)mt t n +≥+,即222(4)(64)90m t m n t n -+-+-≥. 由题意知,042≠-m ,且上式对一切实数t 恒成立,所以A BCD E FGM N⎪⎩⎪⎨⎧≤----=∆>-,0)9)(4(4)46(,042222n m n m m 22,4(6)0,m mn >⎧⇒⇒⎨-≤⎩⎩⎨⎧=>,6,2mn m 所以⎩⎨⎧==,2,3n m 或⎩⎨⎧==.1,6n m 证明 设MN 与EF 交于点P ,∵NE //BC ,∴△PNE ∽△PBC ,∴PCPEPB PN =, ∴PC PN PE PB ⋅=⋅.又∵ME //BF ,∴△PME ∽△PBF ,∴PFPEPB PM =, ∴PF PM PE PB ⋅=⋅. ∴PF PM PC PN ⋅=⋅,故PFPCPN PM = 又∠FPN =∠MPE ,∴△PNF ∽△PMC ,∴∠PNF =∠PMC ,∴NF//MC∴∠ANF =∠EDM.又∵ME//BF ,∴∠FAN =∠MED.∴∠ANF +∠FAN =∠EDM +∠MED ,∴∠AFN=∠DME.解 观察易知,方程有一个整数根11=x ,将方程的左边分解因式,得[]056)18()1(2=+++-x a x x因为a 是正整数,所以关于x 的方程056)18(2=+++x a x (1)的判别式0224)18(2>-+=∆a ,它一定有两个不同的实数根.而原方程的根都是整数,所以方程(1)的根都是整数,因此它的判别式224)18(2-+=∆a 应该是一个完全平方数.设22224)18(k a =-+(其中k 为非负整数),则224)18(22=-+k a ,即224)18)(18(=-+++k a k a .显然k a ++18与k a -+18的奇偶性相同,且1818≥++k a ,而8284562112224⨯=⨯=⨯=,所以⎩⎨⎧=-+=++,218,11218k a k a 或⎩⎨⎧=-+=++,418,5618k a k a 或⎩⎨⎧=-+=++,818,2818k a k a 解得⎩⎨⎧==,55,39k a 或⎩⎨⎧==,26,12k a 或⎩⎨⎧==,10,0k a 而a 是正整数,所以只可能⎩⎨⎧==,55,39k a 或⎩⎨⎧==.26,12k a当39=a 时,方程(1)即056572=++x x ,它的两根分别为1-和56-.此时原方程的三个根为1,1-和56-. 当12=a 时,方程(1)即056302=++x x ,它的两根分别为2-和28-.此时原方程的三个根为1,2-和28-.ABCDE F MN P第二试 (B )解 因为一元二次方程03)3(2=--+mt x mt x 的两根分别为mt 和3-,所以31+=mt d ; 一元二次方程02)2(2=+-+-nt x n t x 的两根分别为t 2和n -,所以n t d +=22. 所以,21d d ≥22)2()3(23n t mt n t mt +≥+⇔+≥+⇔09)46()4(222≥-+-+-⇔n t n m t m (1)由题意知,042≠-m ,且(1)式对一切实数t 恒成立,所以⎪⎩⎪⎨⎧≤----=∆>-,0)9)(4(4)46(,042222n m n m m 22,4(6)0,m mn >⎧⇒⇒⎨-≤⎩⎩⎨⎧=>,6,2mn m 所以⎩⎨⎧==,2,3n m 或⎩⎨⎧==.1,6n m 解 联立方程组⎪⎩⎪⎨⎧=-+++=,56,38)17(2x y a x a x y 消去y 得a x a x -+++38)17(2x 56=,即 056)38()17(23=--+++x a x a x ,分解因式得[]056)18()1(2=+++-x a x x (1)显然11=x 是方程(1)的一个根,(1,56)是两个函数的图象的一个交点. 因为a 是正整数,所以关于x 的方程056)18(2=+++x a x (2)的判别式0224)18(2>-+=∆a ,它一定有两个不同的实数根.而两个函数的图象的交点都是整点,所以方程(2)的根都是整数,因此它的判别式224)18(2-+=∆a 应该是一个完全平方数.设22224)18(k a =-+(其中k 为非负整数),则224)18(22=-+k a ,即224)18)(18(=-+++k a k a .显然k a ++18与k a -+18的奇偶性相同,且1818≥++k a ,而8284562112224⨯=⨯=⨯=,所以⎩⎨⎧=-+=++,218,11218k a k a 或⎩⎨⎧=-+=++,418,5618k a k a 或⎩⎨⎧=-+=++,818,2818k a k a 解得⎩⎨⎧==,55,39k a 或⎩⎨⎧==,26,12k a 或⎩⎨⎧==,10,0k a 而a 是正整数,所以只可能⎩⎨⎧==,55,39k a 或⎩⎨⎧==.26,12k a当39=a 时,方程(2)即056572=++x x ,它的两根分别为1-和56-,此时两个函数的图象还有两个交点)56,1(--和)1,56(--.当12=a 时,方程(2)即056302=++x x ,它的两根分别为2-和28-,此时两个函数的图象还有两个交点)28,2(--和)2,28(--.解 联立方程组⎪⎩⎪⎨⎧-=-+++=,311,710)232(22x ay a x a x y 消去y 得a x a x 710)232(22-+++= 113ax-,即0113)710()232(223=-+-+++a x a x a x ,分解因式得 []0311)12()12(2=-+++-a x a x x (1)如果两个函数的图象有公共整点,则方程(1)必有整数根,从而关于x 的一元二次方程0311)12(2=-+++a x a x (2)必有整数根,所以一元二次方程(2)的判别式∆应该是一个完全平方数,而224)18(10036)311(4)12(222-+=++=--+=∆a a a a a .所以224)18(2-+a 应该是一个完全平方数,设22224)18(k a =-+(其中k 为非负整数),则224)18(22=-+k a ,即224)18)(18(=-+++k a k a .显然k a ++18与k a -+18的奇偶性相同,且1818≥++k a ,而8284562112224⨯=⨯=⨯=,所以⎩⎨⎧=-+=++,218,11218k a k a 或⎩⎨⎧=-+=++,418,5618k a k a 或⎩⎨⎧=-+=++,818,2818k a k a 解得⎩⎨⎧==,55,39k a 或⎩⎨⎧==,26,12k a 或⎩⎨⎧==,10,0k a 而a 是正整数,所以只可能⎩⎨⎧==,55,39k a 或⎩⎨⎧==.26,12k a当39=a 时,方程(2)即0106512=-+x x ,它的两根分别为2和53-,易求得两个函数的图象有公共整点)53,2(-和)2,53(-.当12=a 时,方程(2)即025242=-+x x ,它的两根分别为1和25-,易求得两个函数的图象有公共整点)25,1(-和)1,25(-.。
2007年初中数学竞赛试题赏析(含解答)-
2007年初中数学竞赛试题赏析2007年春末夏初,国内的初中数学竞赛基本告一段落,暑假期间,在放松避暑纳凉的同时,对数学爱好者来说,把玩一下新的试题,也是一件乐事.下面为大家选析一些试题,供同学们玩赏.一、代数问题例1 已知a ,b ,c 是实数,若2222b c a bc +-,2222c a b ac +-,2222a b c ab+-之和恰等于1,求证:这三个分数的值有两个为1,一个为-1.(2007年北京市初二数学竞赛试题三)证明 由题设2222b c a bc +-+2222c a b ac +-+2222a b c ab+-=1, 即(2222b c a bc +--1)+(2222a c b ac +--1)+(2222a b c ab+-+1)=0, 通分,分子部分因式分解,(请自己完成演算)可得()()()2a b c c a b c a b abc+-+--+=0. 所以,或者a+b-c=0或者c+a-b=0或者b+c-a=0.①若a+b-c=0,则222222222222222222()21;222()21;222()2 1.222b c a b c b c bc bc bc bcc a b c a c a ac ac ac cab c a a b a b ab bc ab ab+-+--===+-+--===+-+-+-===- ②若c+a-b=0,同理可得2222b c a bc +-=1,2222c a b ac +-=-1,2222a b c ab+-=1, ③若c+a-b=0,同理可得2222b c a bc +-=-1,2222c a b ac +-=1,2222a b c ab+-=1. 综合①、②、③可得,三个分数2222b c a bc +-,2222c a b ac +-,2222a b c ab+-的值有两个为1,一个为-1.评析:由题设2222b c a bc +-+2222c a b ac +-+2222a b c ab+-=1,要证这三个分数的值有两个为1,一个为-1,想到证(2222b c a bc +--1)+(2222a c b ac +--1)+(2222a b c ab+-+1)=0 是关键.其中分子部分的因式分解,可检验你的代数式恒等变形的基本功是否过硬. 例2 设a 是正整数,二次函数y=x 2+(a+17)x+38-a ,反比例函数y=56x,•如果这两个函数的图象的交点都是整点(横坐标和纵坐标都是整数的点),求a 的值.(2007年全国初中数学联合竞赛(B 组)试题第三大题)解 联立方程组2(17)38,56,y x a x a y x ⎧=+++-⎪⎨=⎪⎩消去y 得x 2+(a+17)x+38-a=56x, 即x 3+(a+17)x 2+(38-a )x-56=0,分解因式得(x-1)[x 2+(a+18)x+56]=0. (1)显然x 1=1是方程(1)的一个根,(1,56)是两个函数的图象的一个交点, 因为a 是正整数,所以关于x 的方程x 2+(a+18)x+56=0 (2)的判别式△=(a+18)2-224>0,它一定有两个不同的实数根.而两个函数的图象的交点都是整点,所以方程(2)的根都是整数,•因此它的判别式△=(a+18)2-224应该是一个完全平方数.设(a+18)2-224=k 2(其中k 为非负整数),则(a+18)2-k 2=224,即(a+18+k )(a+18-k )=224.显然a+18+k 与a+18-k 的奇偶性相同,且a+18+k ≥8,而224=112×2=56×4=28×8,18112,1856,1828,182,184,188.39,12,0,55,26,10.a k a k a k a k a k a k a a a k k k ++=++=++=⎧⎧⎧⎨⎨⎨+-=+-=+-=⎩⎩⎩===⎧⎧⎧⎨⎨⎨===⎩⎩⎩所以或或解得或或 而a 是正整数,所以只可能39,12,55,26,a a k k ==⎧⎧⎨⎨==⎩⎩或 当a=39时,方程(2)即x 2+57x+56=0,它的两根分别为-1和-56,此时两个函数的图象还有两个交点(-1,-56)和(-56,-1).当a=12时,方程(2)即x 2+30x+56=0,它的两根分别为-2和-28,此时两个函数的图象还有两个交点(-2,-28)和(-28,-2).评析:这是初中数学的重点知识与方法高度综合的题目,要求会自行演算独立解答.二、几何问题在初中阶段,图形的运动主要是合同变换,包含平移、轴对称、旋转和中心对称.另外,在我国的几何教学中,对等积变换的知识日益普及,主要是利用“同底等高的两个三角形面积相等”和三角形面积公式来证题、计算,包括解决线段的比例问题.例3 如图1所示,△ABC 中,∠ABC=46°,D 是BC 边上一点,DC=AB ,∠DAB=21°,•试确定∠CAD 的度数.(2007年北京市中学生数学竞赛初二年级试题四)图1 图2解如图2,作△ABD关于AD的轴对称图形△AED,即∠EAD=21°,AE=AB,•所以DE=BD.易知∠ADC=21°+46°=67°,所以∠ADE=∠ADB=180°-67°=113°,∠CDE=113°-67°=46°,连接CE,DC=AB,△ABD≌△CDE≌△ADE.设O为AE与DC的交点,由于∠ODE=∠OED=46°,所以OD=OE.又DC=AE,所以AO=CO ∠OCA=∠OAC ∠COE=2∠ACO.易知∠COE=2×46°=92°,因此2∠ACO=∠COE=92°∠ACO=46°=∠OAC.所以∠DAC=∠DAE+∠EAC=21°+46°=67°.例4如图3,已知等腰△ABC中,AB=AC,P、Q分别为AC、AB上的点,且AP=PQ=•QB=BC,则∠PCQ=______.(2007年北京市中学生数学竞赛初二年级试题)图3 图4解:如图4,过P作AB的平行线,过B作PQ的平行线,二平行线相交于O,则PQBO•是个菱形.连接CO.由AB=AC,AP=QB,则PC=AQ,AP=QB=PO,∠CPO=∠PAQ,所以△PQC≌△APQ,因此CO=PQ=CB=OB,可知△BCO为等边三角形,∠BCO=∠CBO=60°,•设∠CAB=θ,•则∠PCO=∠QBO=θ,由三角形内角和定理,得3θ+2×60°=180°⇒θ=20°,因此∠PCQ=80°-•50°=30°.例5 如图5,四边形ABCD 是梯形,点E 是上底AD 边上一点,CE 的延长线与BA 的延长线交于点F ,过点E 作BA 的平行线CD 交的延长线于点M ,BM 与AD 交于点N .证明:∠AFN=∠DME .(2007全国初中数学联合竞赛试题)例5分析 延长BF ,CM 相交于Q ,因为EM ∥AF ,所以∠DME=∠DQA .要证∠AFN=∠DME ,只需证∠AFN=∠DQA 即可.为此,只需证FN ∥MC .证明 (面积法)连接FM ,BE ,CN ,因为EM ∥AF ,所以S △PFM =S △PBE ,因为AD ∥BC ,S △BNE =S △CNE ,因此S △BNE +S △PNE =S △CNE +S △PNE .即S △PBE =S △PNC ,所以S △PFM =S △PNC .两边同加S △PMC 得S △FMC =S △NMC ,所以FN ∥MC ,又已知FB ∥ME ,所以∠AFN=∠DME .至于其它的证法我们就不再例举了.例6 试问:18能否表示为3个互异的正整数的倒数的和?18能否表示为3•个互异的完全平方数的倒数的和?如果能,请给出一个例子;如果不能,请说明理由. (第12届华杯赛初一组决赛试题14)解:(1)由于18=14×12=14×(112+16+14)=114824++116,所以18能表示为3个互异的正整数的倒数的和.(2)不妨设三个正整数a<b<c ,满足18=21a +21b +21c. 由于a ,b ,c 是互异的正整数,则21c <21b <21a, 从而18=21a +21b +21c <23a ,所以a 2>24.又18>21a,所以a 2>8,故a 2=9或16. 若a 2=9,则21b +21c =18-19=172,于是172>21b,有b 2>72; 又因为21c <21b ,所以172=21b +21c <22b , 因此b 2<144,所以72<b 2<144.故b 2=81,100或121,将b 2=81,100,121分别代入c 2=227272b b -,没有一个是完全平方数,此时无解.若a 2=16,则21b +21c =18-116=116, 同上讨论可得:16<b 2<32,所以b 2=25,c 2=22161625169b b ⨯=-不是整数. 综上所述,18不能表示为3个互异的完全平方数的倒数之和. 例7 已知a ,b 都是正整数,试问关于x 的方程x 2-abx+12(a+b )=0是否有两个整数解?如果有,请把它们求出来;如果没有,请给出证明.解 不妨设a ≤b ,且方程的两个整数根为x 1,x 2(x 1≤x 2),则有12121()2x x ab x x a b +=⎧⎪⎨=+⎪⎩ 所以x 1x 2-x 1-x 2=12a+12b-ab ,4(x 1-1)(x 2-1)+(2a-1)(2b-1)=5. 因为a ,b 都是正整数,所以x 1,x 2均是正整数.于是x 1-1≥0,x 2-1≥0,2a-1≥1,2b-1≥1,所以12(1)(1)0(21)(21)5x x a b --=⎧⎨--=⎩或12(1)(1)1(21)(21)1x x a b --=⎧⎨--=⎩ (1)当12(1)(1)0(21)(21)5x x a b --=⎧⎨--=⎩时,由于a ,b 都是正整数,且a ≤b ,可得a=1,b=3. 此时,一元二次方程为x 2-3x+2=0,它的两个根为x=1,x=2.(2)当12(1)(1)1(21)(21)1x x a b --=⎧⎨--=⎩时,可得a=1,b=1,此时,一元二次方程为x 2-x+1=0,它无整数解.综上所述,当且仅当a=1,b=3时,题设方程有整数解,且它的两个整数解为x 1=1,x 2=2.例8 (1)是否存在正整数m ,n ,使得m (m+2)=n (n+1)?(2)设k (k ≥3)是给定的正整数,是否存在正整数m ,n ,使得m (m+k )=n (n+1)? 解:(1)答案是否定的.若存在正整数m ,n ,使得m (m+2)=n (n+1). 则(m+1)2=n 2+n+1,显然n>1.于是n 2<n 2+n+1<(n+1)2,所以n 2+n+1不是平方数,矛盾.(2)当k=3时,若存在正整数m ,n ,使得m (m+3)=n (n+1),则4m 2+12m=4n 2+4n ⇔(2m+3)2=(2n+1)2+8即(2m+3-2n-1)(2m+3+2n+1)=8⇔ (m-n+1)(m+n+2)=2, 而m+n+2>2,故上式不可能成立.当k ≥4时,若k=2t (t 是不小于2的整数)为偶数,取m=t 2-t ,n=t 2-1,则m (m+k )=(t 2-t )(t 2+t )=t 4-t 2,n (n+1)=(t 2-1)t 2=t 4-t 2,因此这样的(m ,n )满足条件.若k=2t+1(t是不小于2的整数)为奇数,取m=22t t-,n=222t t+-,则m(m+k)=22t t-(22t t-+2t+1)=14(t4+2t3-t2-2t)n(n+1)=222t t+-·22t t+=14(t4+2t3-t2-2t),因此这样的(m,n)满足条件.综上所述,当k=3时,答案是否定的;当k≥4时,答案是肯定的.(注:当k≥4时,构造的例子不是唯一的.)四、组合与极值组合问题对锻炼思维意义重大,初中只适宜分类计数、加法原理、乘法原理的简单运用,简单的包含排除原理,基本的抽屉原理也是重要的内容.但在初中阶段,不应提前引入排列组合的计算公式.特别是提前较大范围的培训高中的排列组合知识,会激起大范围超前学习的竞争热,从而影响基础教育,并且也影响竞赛的公平性.建议命一些以几何元素为背景的构造性的问题,容易引发学生兴趣,又使套用组合公式的人容易出错,这类问题的研制特别引人注目.例9 平面上有6个点,其中任何3个点不在同一条直线上,以这6个点为顶点可以构造多少个不同的三角形?从这些三角形中选出一些,如果要求其中任何两个三角形没有公共点,则最多可以选出多少个三角形?(第12届华杯赛初一组决赛试题12)解答:(1)先从6个点中选取1个做三角形的一个顶点,有6种取法;•再从余下的5点中选取1个做三角形的第二个顶点,有5种取法;再从余下的4个点中选取1个点做三角形的第三个顶点者,有4种取法.因为任何3个点不在同一条直线上,所以,这样选出的三个点可以做出一个三角形.但是,如果选出的三个点相同的话,则做出的三角形相同,•三个点相同的取法有3×2×1=6种,所以,以这6个点为顶点可以构造654321⨯⨯⨯⨯=20个不同的三角形.(2)每个三角形有3个顶点,所以,6个点最多只能做出2个三角形,•它们没有公共顶点,如图4(1).(3)用英文大写字母A,B,C,D,E,F记这6个点,如果可以选出5个三角形,它们共有15个顶点,需要15个英文大写字母.但是,不同的英文大写字母仅有6个,因此,这5•个三角形中至少有三个三角形有同一个顶点,不妨设为点A.根据题目条件,这三个三角形没有公共边,即除去公共顶点A之外,其余6•个顶点互不相同,即表示这6个顶点的字母不相同.否则,根据题目条件,它们将有公共边.但是,除A之外,我们仅有5个不同的字母,所以,不可能存在5个三角形,它们没有公共边.如图4(2)所示,△ABC,△ADE,△BDF和△CEF这4个三角形没有公共边,所以,最多可以选出4个三角形,它们没有公共边.例10 若对于任意n个连续正整数中,总存在一个数的数字之和8是的倍数.试确定n的最小值,并说明你的理由.(2007北京市中学生数学竞赛初二年级试题五)解先证n≤14时题设的性质不成立.因为,当n=14时,对于9999993,9999994,…,999999,…,10000006这14个连续整数中,任意一个数字的数字之和均不能被8整除.所以n≤14时题设的性质不成立.因此要使题设的性质成立,应有n≥15.再证n=15时,题设的性质成立.设a1,a2,…,a15为任意的连续15个正整数,则这15个正整数中,个位数字为0•的整数最多有两个,最少有一个,可分为:(1)当a1,a2,…,a15中个位数字为0的整数有两个时,设a i<a j,且a i,a j的个位数字为0.则满足a i,a i+1,a i+2,…,a i+9,a j为连续的11个整数,其中a i,a i+1,a i+2,…,a i+9无进位设n i表示a i各位数字之和.则前10个数的各位数字之和分别为n i,n i+1,…,n i+9则这连续的10个数中至少有一个被8整除.(2)当a1,a2,…,a15中个位数字为0的整数只有一个时,设其中的a i的个位数字为0,•①若整数满足1≤i≤8,则在a i后面至少有7个连续整数,则a i,a i+1,a i+2,…,a i+7这8个连续整数的各位数字和也为8个连续整数,所以必有一个数能被8整除.②若整数i满足9≤i≤15,则在a前面至少有8个连续整数,不妨设为a i-8,a i-7,a i-5,a i-4,a i-3,a a-2,a a-2,a i-1,这8个连续整数的各位数字和也为8个连续整数,所以必有一个数能被8整除.由①、②可知,当a1,a2,…,a15中个位数字为0的整数只有一个时,必有一个数,其各位数字之和是8的倍数.综上(1)、(2)所述,对于任意15个连续整数中,必有一个数,•其各位数字之和是的倍数.而小于15个的任意连续整数不成立此性质,所以n的最小值是15.例11 平面上有若干个点,其中任意三点都不在同一直线上,将这些点分成三组,并按下面的规则用线段连接:①在同一组的任意两点都没有线段连接;②不在同一组的任意两点间一定有线段连接.(1)若平面上恰好有9个点,且平均分成三组,那么平面上有多少条线段?(2)若平面上恰好有9个点,且点数分成2,3,4三组,那么平面上有多少条线段?(3)若平面上共有192条线段,那么平面上至少有多少个点?(第十八届“希望杯”全国数学邀请赛初二第2试23题)解:(1)平面上恰好有9个点,且平均分成三组,每组3个点,•按题设规则用线段连接,可以连出3×3+3×3+3×3=27条线段.(2)平面上恰好有9个点,且点数分成2,3,4三组,按题设规则用线段连接,可以连出2×3+2×4+3×4=26条线段.(3)设平面上三组点数为m,n,p个,s=m+n+p,目标求s的最小值?按题设规则用线段连接,可以连出mn+mp+np=192条线段.由于s2=(m+n+p)2=m2+n2+p2+2mn+2mp+2np≥mn+mp+np+2mn+2mp+2np=3mn+3mp+3np=•3(mn+mp+np)=3×192=576=242所以s≥24.s的最小值是24.事实上,当这24个点平分为3组,每组8个点,按题设规则用线段连接,恰可以连出8×8+8×8+8×8=3×64=192条线段.因此平面上至少有24个点.- 11 -。
[“数学周报杯”2007]2007年“数学周报杯”全国初中数学竞赛初赛试题(含答案)
频数(学生人数) 16 12 10 8 E
F m O(D) C
B
50 60 70 80 90 100 成绩(分) (注:每组不含最小值,含最大值)
24、 (本题 7 分)小宇同学在布置班级文化园地时,想从一块长为 20cm,宽为 8cm 的长方形 彩色纸板上剪下一个腰长为 10cm 的等腰三角形,并使其一个顶点在长方形的一边上,另两个顶点 落在对边上,请你帮他计算出所剪下的等腰三角形的底边长。 25、 (本题 8 分)在修建某条公路的过程中,需挖通一条隧道,甲、乙两个工程队从隧道两端 同时开始挖掘。施工期间,乙队因另有任务提前离开,余下的 任务由甲队单独完成,直至隧道挖通。下图是甲、乙两个工程 y /米 队所挖隧道的长度 y (米)与挖掘时间 x (天)之间的函数图 象,请根据图象所提供的信息解答下列问题: (1)求该隧道的长; (2)乙工程队工作多少天时,两队所挖隧道的长度相差 18 米? 432
C、30°或 60°
D、30°或 90°
17、 平面直角坐标系中, 若一个点的横、 纵坐标都是整数, 则称该点为整点。 若函数 y = 2 x 1 与 y = kx + k 的图象的交点为整点时,则整数 k 的值可取( )
A、2 个 B、3 个 C、4 个 D、5 个 18、如图,△ABC 的面积为 60,点 D 在 BC 上,BD=2CD, A 连接 AD,点 E 为 AD 中点,连接 BE 并延长交 AC 于点 F,则△ AEF 的面积为( ) F E A、2 B、4 C、5 D、8 19、甲、乙二人从 M 地同时出发去 N 地,甲用一半时间以每小时 a 千米的速度行走,另一半时间以每小时 b 千米的速度行走;乙 B C D 以每小时 a 千米的速度行走一半路程,另一半路程以每小时 b 千 米的速度行走。若 a ≠ b ,则下列说法正确的是( ) A、二人同时到达 N 地 B、甲先到达 N 地 C、乙先到达 N 地 D、若 a > b ,甲先到达 N 地;若 a < b ,乙先到达 N 地 20、一些完全相同的小正方体搭成一个几何体,这个几何体从正面和左面看所得的平面图形 均为右图所示,小正方体的块数可能有( ) A、7 种 B、8 种 C、9 种 D、10 种
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007年全国初中数学竞赛(海南赛区)初赛试卷(本卷满分120分,考试时间:3月18日8:30——10:30)一、选择题(本大题满分50分,每小题5分)在下列各题的四个备选答案中,只有一个是正确的,请把正确的答案的字母代号填写括号内.1.若m 为实数,则代数式m +m 的值一定是( ).A 、正数B 、0C 、负数D 、非负数2.如图1所示,是两架处在平衡状态的天平,那么,对于a 、b 、c 三种物体的重量,下列判断正确的是( ).A 、c >aB 、a <bC 、a <cD 、b <c3.如图2,点C 是∠P AQ 的平分线上一点,点B 、B ′分别在边AP 、AQ 上,如果再添加一个条件,即可推出AB =AB′,那么该条件不可以是( ).A 、BB′⊥ACB 、CB =CB ′C 、∠ACB =∠ACB ′D 、∠ABC =∠AB ′C4.图3是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的两条直角边长分别为a 、b ,则(a +b )2的值是( ).A 、13B 、19C 、25D 、1695.已知m 是方程01x -x 2=+2006的一个根,则代数式 3+1++22m 20062005m -m 的值等于( ). A 、2005 B 、2006 C 、2007 D 、.20086.将一段72cm 长的绳子,从一端开始每3cm 作一记号,每4cm 也作一记号,然后从有记号的地方剪断,则这段绳子共被剪成的段数为( ).A 、37B 、36C 、35D 、347.某旅游团92人在快餐店就餐,该店备有9种菜,每份菜单单价分别为1、2、3、4、5、6、7、8、9(元),旅游团领队交代:每人可选不同的菜,但金额都须正好10元,且每一种菜最多只能买一份,这样,该团成员在购菜完全符合要求的所有方案中,至少有一个方案的人数不少于( ).A 、9人B 、10人C 、11人D 、12人8.如图4是由几块相同的小正方体搭成的立体图形的三视图,则这立体图形中小正方体共有( )块.A 、9B 、10C 、11D 、12图 2图1 图39.如图5,将△ABC 沿着它的中位线DE 折叠后,点A 落到点A ′,若∠C =120 ,∠A =26 ,则∠A ′DB 的度数是( ). A 、120 B 、112 C 、110 D 、10810.方程222x x x-=的正根的个数是( ). A 、0个 B 、1个 C 、2个 D 、3个二、填空题(本大题共8小题,每小题5分,满分40分)11.若[]x 表示不超过x 的最大整数,如[][][]3233740.70..=-=-=,,等,则[]3p +-=_________ 12.在直径为4cm 的⊙O 中,长度为32cm 的弦BC 所对的圆周角的度数为 .13.如图6,电路图上有四个开关A 、B 、C 、D 和一个小灯泡,闭合开关D 或同时闭合开关A 、B 、C 都可以使小灯泡放光,那么随机闭合其中两个开关,能使小灯泡发光的概率为 .14.如图7,在△ABC 中,AB =5,AC =3,D 为BC 的中点,AD =2,则tan ∠BAD = __________.15.若干个工人装卸一批货物,每个工人的装卸速度相同,如果这些工人同时工作,则需10小时装卸完毕;现改变装卸方式,开始一个人干,以后每隔t (整数)小时增加一个人干,每个参加装卸的人都一直干到装卸完毕,且最后参加的一个人 装卸的时间是第一个人的41,则按改变的方式装卸, 自始至终共需时间 小时.16.在一次自行车越野赛中,甲、乙两名选手所走的路程y (千米)随时间x (分钟)变化的图象(全程)分别用图8中的实线(O→A→B→C )与虚线(OD )表示,那么,在本次比赛过程中,乙领先甲时的x 的取值范围是 .17.已知a <3,b >3,且1a b k +=-,ab =3,则k 的最小整数值是_____________.18.若30350x y z x y z ++=+-=,, 且x 、y 、z 均为非负数,则542M x y z =++的最大值为________.三、解答题(本大题共2小题,每小题15分,满分30分)19.已知在△ABC 中,∠ACB =90 ,AC =BC =4,现将一块边长足够大的直角三角板的直角顶点置于AB 的中点O ,两直角边分别经过点B 、C ,然后将三角板绕点O 按顺时针方向旋转一个角度 0(α<α<90 ),旋转后,直角三角板的直角边分别与AC 、BC 相交于点K 、H ,四边形CHOK 是旋转过程中三角板与△ABC 的重叠部分(如图所示).那么,在上述旋转过程中:(1)线段BH 与CK 具有怎样的数量关系?四边形CHOK 的面积是否发生变化?证明你发现的结论;(2)连接HK ,设BH =x ,①当△CKH 的面积为32时,求出x 的值; ②试问△OKH 的面积是否存在最小值,若存在,求出此时x 的值,若不存在,请说明理由.20.某农机租赁公司共有50台收割机,其中甲型20台、乙型30台,现将这50台联合收割机派往A 、B 两地区收割水稻,其中30台派往A 地区,20台派往B 地区,两地区与该农机公司商定的每天租赁价格如下表:(1)设派往A 地区x 台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y 元,求y 关于x 的函数关系式;(2)若使农机租赁公司这50台收割机一天所获租金不低于79600元,试写出满足条件的所有分派方案;(3)农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由。
2007年全国初中数学竞赛初赛(海南赛区)参考答案一、选择题:1、D ;2、A ;3、B ;4、C ;5、D ;6、B ;7、C ;8、A ;9、B ;10、A .1.提示:若m ≥0,则|m |+m =2m ≥0;若m <0,则|m |+m =-m +m =0,故选D ;2.提示:由左天平知a >b ,由右天平知b >c ,∴a >c 故选A ;3.提示:由已知条件和选项B 不能保证△ACB ≌△ACB ′,从而无法推出AB =AB ′,故选B ;4.提示:依题意知(a -b )2=1,∴a 2-2ab + b 2=1,又∵a 2+ b 2=13,∴2ab =12,∴(a +b )2=a +2ab +b 2=13+12=25,故选C ;5.由已知条件得m 2-2006m +1=0,∴m 2-2005m = m -1,m 2+1= 2006m ,于是原式=m -1+20062006m +3=-1+1m +3= 2+1m m m-+3=2006m m m -+3=3005+3=2008,故选D ; 6.提示:每隔3cm 剪一刀共剪72÷3-1=24-1=23(刀),每隔4cm 剪一刀, 共剪72÷4-1=17(刀),所以应共剪23+17=40(刀),但其中重复位置的刀数为: 72÷12-1=5(刀),因此互不重复的刀数为40-5=35(刀),所以72cm 长的绳子 按要求被剪的段数为35+1=36(段),故选B ,7.提示:因为每份菜单价为别为1、2、3、4、5、6、7、8、9(元),共9种菜,所有符合要求的购菜方案为:1+9,2+8,3+7,4+6,1+2+7,1+3+6,1+4+5,2+3+5,1+2+3+4,共9种,又共有92人就餐,∴92÷9=10…余2,故选C ;8.提示:从俯视图知该立体图形从前到后共排了三排小正方体,各位置上小正方体的个数如图所示,故选A ;9.提示:分别延长BD ,CE 相交,则交点即为点A ,由三角形中位线的性质知DE ∥BC ,∴∠ADE =∠B =180°-∠C -∠A=180°-120°-26°=34°,又由轴对称的性质知∠A ′DE =∠ADE =34°, ∴∠A ′DB =180°-2×34°, ∴∠A ′DB =180°-2×34°=112°,故选B ;10.提示,分别画出函数22y x x =-和2yx=(x >0)图象 (如图所示),因为函数22y x x =-和2y x=的图象在第一 象限内无交点,因此,方知222x x x-=无正数根,故选A . 另解:令2x -x 2=0,解得x 1=0,x 2=2,易知方程222x x x -=的 正数解x 的值的范围应是0<x <2,而此时2x -x 2=-(x -1)2+1≤1,2x >1,因此,原方程无正数解。
二、填空题:11.10;12.60°或120°;13.12;14.34;15.16;16.24<x <38;17.-18.130.11.-10,提示:+3〔-π〕=2+3(-4)=2-12=10;12.60°或120°,提示:作⊙O径AB,连结AC,则在△ABC中,AB=4,BC∠C=90°,∴∠A=60°,设BC所对的圆周角为∠P.当∠P的顶点P在BAC上时,∠P=∠A=60°,当∠P的顶点P在劣弧BC上时,∠P+∠A=180°,∴∠P=120°;13.12,提示:画出树状图求解,答案为12;14.34,提示:延长AD到E,使DE=AD=2,连结BE,则△BDE≌△CDA,∴BE=AC=3,又AE=4,AB=5,显然△AEB为Rt△,∠E=90°,∴tan∠BAD=BEAD=34;15.16,提示:设自始至终需x小时,由于每个工人的装卸速度相同,且工作时间是等差递减的,因此,这些工人的装卸时间的平均数为12·(x+14x);于是得:方程12·(x+14x)=10.16.24<x<38,提示:分别求线段AB、BC与线段OD的交点的横坐标.17.6. 提示:∵a<3,b>3,∴a-3<0,b-3>0,∴(a-3)(b-3)<0,∴ab-3(a+b)+9<0,又∵a+b=k-1,ab=3,代入上述不等式,得3-3(k-1)+9<0,解得k>5.18.130,提示:由30350x y zx y z++=⎧⎨+-=⎩用x来表示y、z,得y=40-2x,z=x-10,又由y≥0,z≥0,得402xx-≥0⎧⎨-10≥0⎩解得10≤x≤20,又把y=40-2x,z=x-10代入M=5x+4y+2z得,M=-x+140,显然M是关于x的一次函数,且M随x增大而减小,所以当x=10时,M 的最大值为130.三、解答题:19.(1)在旋转过程中,BH=CK,四边形CHOK的面积始终保持不变,其值为△ABC 面积的一半.理由如下:连结OC∵△ABC为等腰直角三角形,O为斜边AB的中点,CO⊥AB;∴∠OCK=∠B=45°,CO=OB,又∵∠COK与∠BOH均为旋转角,∴∠COK=∠BOH=α,∴△COK≌△BOH,∴BH=CK,S四边形CHOK=S△COK+S△COH=S△BOH+S△COH=S△COB=12S△ABC=4.(2)①由(1)知CK=BH=x,∵BC=4,∴CH=4-x,根据题意,得12CH·CK=32,即(4-x)x=3,解这个方程得x1=1,x2=3,此两根满足条件:0<x<4所以当△CKH的面积为3 2时,x的取值是1或3;②设△OKH的面积为S,由(1)知四边形CHOK的面积为4,于是得关系式:S=4-S△CKH=4-12x(4-x)=12(x2-4x)+4=12(x2-2)+2当x=2时,函数S有最小值2,∵x=2时,满足条件0<x<4,∴△OKH的面积存在最小值,此时x的值是2.20.(1)由于派往A地的乙型收割机x台,则派往B地的乙型收割机为(30-x)台,派往A、B地区的甲型收割机分别为(30-x)台和(x-10)台.∴y=1600x+1200(30-x)+1800(30-x)+1600(x-10)=200x+74000(10≤x≤30)(2)由题意,得200x+74000≥79600,解得x≥28,∵10≤x≤30,x是正整数∴x=28、29、30∴有3种不同分派方案:①当x=28时,派往A地区的甲型收割机2台,乙型收割机28台,余者全部派往B地区;②当x=29时,派往A地区的甲型收割机1台,乙型收割机29台,余者全部派往B地区;③当x=30时,即30台乙型收割机全部派往A地区,20台甲型收割机全部派往B地区;(3)∵y=200x+74000中y随x的增大而增大,∴当x=30时,y取得最大值,此时,y=200×30+74000=80000,建议农机租赁公司将30台乙型收割机全部派往A地区,20台甲型收割机全部派往B地区,这样公司每天获得租金最高,最高租金为80000元.。
