连续介质力学-第1章-四川大学
合集下载
第一章 四川大学高分子流变
2rl rz pr 0
2
在一定压力梯度（△p/L）下，剪切应力同离开轴的距离成 正比，且与流体性质无关。
在轴上，剪切应力为零，在管壁上剪切应力的最大值为
rz
pr 2L
管壁处
R max
管中心处
pR 2L
0
牛顿流体分布
dvz pr dr 2l
积 分
速度分布式
n p v(r ) n 1 2 KL
1 n 1 nn n R r 1 n 1 n 1 n n r n p R n 1 n 1 2 KL R
1 n
(8 4)
改 写
则体积流率为
qv
R
0
n p v(r )2rdr R 3n 1 2 KL
1 n
3 n 1 n
(8 5)
式中令n=1，K=μ，就为牛顿流体流率
w
1 dQ 1 Qd ln Q ( 3 Q ) (3 Q ) w 3 3 R d w R d ln w
4Q 3 1 d ln Q 1 1 d ln a ( ) ( ) a 3 R 4 4 d ln w 4 4 d ln w
－－Rabinowitsch方程 上式反映了非牛流体偏离牛顿流体的程度
1 0.4 w M Z 1 B M E( ) B RT Mw
熔体破裂 是挤出物表面出现凹凸不平或外形发生畸变以致 支离或断裂的总称。
不仅影响挤出产量， 也影响挤出制品的质量
流动是稳定的，剪切应力随剪切速 率“线性”增加（幂律行为），挤 出物具有光滑的外表 当剪切应力达到第一临界值 cr1 时， 在挤出物表面出现小幅度的周期性 的畸变，这是流动曲线的斜率也有 变化 这种不稳定性称为鲨鱼皮症或表面 熔体破裂
连续介质力学作业(第一章参考答案)
(
)
5
x ⋅ S ⋅ x = xm g m ⋅ =
1 ij S − S ji g i g j ⋅ xn g n 2
(
)
1 ij S − S ji xm x n g m ⋅ g i g j ⋅ g n 2 1 = S ij − S ji xm xn δim δ n j 2 1 1 = S ij xi x j − S ji xi x j 2 2 1 1 = S ij xi x j − S ji x j xi 2 2 1 1 = S ij xi x j − S ij xi x j 2 2 =0
其他两个，同理可证。 (1)如果二阶张量 S 是反对称张量，对于任意一阶张量 x ，证明 x ⋅ S ⋅ x = 0 (2) S 是二阶反对称张量， A 是二阶对称张量，证明 A : S = 0
5.
¾
解答：
m
（1） x = xm g
因为二阶张量 S 是反对称张量
S=
1 ij S − S ji g i g j 2
(
)
(
)
（2） S = S g i g j ， A = Amn g g ，
ij m n ij A : S = S ij g i g j : Amn g m g n = S ij Amn δim δ n j = S Aij
S ij Aij = − S ji Aij = − S ji A ji = − S ij Aij
c） R ε g R = ε l 所以
T
1 ⎤ ⎥ 2 ⎥ ⎡1.6 ⎢ 3 ⎥⎣ 0 2 ⎥ ⎦
⎡ 0 ⎤⎢ ⎢ 2.3⎥ ⎦⎢ ⎢ ⎣
3 2 1 2
1⎤ − ⎥ ⎡ 1.775 0.3031⎤ 2⎥ = ⎢ ⎥ 3 ⎥ ⎣0.3031 2.125 ⎦ 2 ⎥ ⎦
连续介质力学-第3章-四川大学
3 应力
n
t (n)
n
t(n) (n) 1
t(n) 2
0
一点的应力状态包括经过这点的所 有方向上的应力矢量
Cauchy定理：
如果空间某点x处的张量 是通过x的微元面 da的法线n的连续函数，则存在比 高一阶的
张量s(x : t)，使
成立。
(x, n; t) s(x; t) n
几个和应力有关的概念：
➢ 三个主应力
➢ 应力的主平面 主应力曲面(3D)，主应力迹线(2D)
➢ 平均正应力，应力偏量
T
1 3
IT I
T
➢ 最大切应力
max
1 2
( 1
3)
1 2
(
1
3)
方向: 与第一主轴和第三主轴成45°的夹角
➢ 八面体应力
oct
n t (n)
如果要求K点处法线方向为 n 的斜截面上的法向应力 ，
只需在该点处的应力张量 T 的前后分别点乘单位矢量 n
即可，即
T11 T12 T13 n1
n T n nT Tn n1
n2
n3 T21
T22
T23
n2
T31 T32 T33 n3
Cauchy应力张量
T11 T12 T13 e1
T (e1
e2
e3 )T21
T22
T23
e
2
Tij ei e
j
T31 T32 T33 e3
对于应力状态，人们常采用单元体的表示方法， 即：将这一点“放大”为一个微元六面体，并取其六 个面分别平行于坐标面，这样的微元六面体就称为单 元体。单元体的六个面上的应力表示过该点的法线方 向与坐标轴正向重合或相反的六个微元面上的应力。 根据作用力与反作用力相等的原理，单元体中相对表 面的应力矢量总是大小相等而方向相反的。
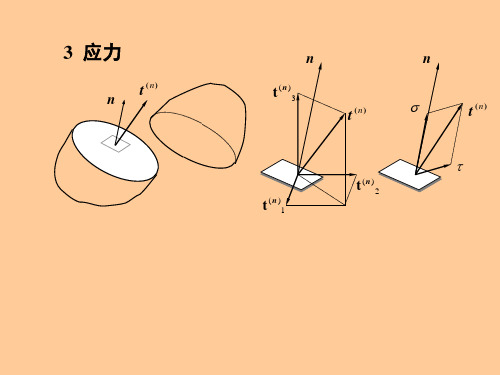
n
t (n)
n
t(n) (n) 1
t(n) 2
0
一点的应力状态包括经过这点的所 有方向上的应力矢量
Cauchy定理：
如果空间某点x处的张量 是通过x的微元面 da的法线n的连续函数，则存在比 高一阶的
张量s(x : t)，使
成立。
(x, n; t) s(x; t) n
几个和应力有关的概念：
➢ 三个主应力
➢ 应力的主平面 主应力曲面(3D)，主应力迹线(2D)
➢ 平均正应力，应力偏量
T
1 3
IT I
T
➢ 最大切应力
max
1 2
( 1
3)
1 2
(
1
3)
方向: 与第一主轴和第三主轴成45°的夹角
➢ 八面体应力
oct
n t (n)
如果要求K点处法线方向为 n 的斜截面上的法向应力 ，
只需在该点处的应力张量 T 的前后分别点乘单位矢量 n
即可，即
T11 T12 T13 n1
n T n nT Tn n1
n2
n3 T21
T22
T23
n2
T31 T32 T33 n3
Cauchy应力张量
T11 T12 T13 e1
T (e1
e2
e3 )T21
T22
T23
e
2
Tij ei e
j
T31 T32 T33 e3
对于应力状态，人们常采用单元体的表示方法， 即：将这一点“放大”为一个微元六面体，并取其六 个面分别平行于坐标面，这样的微元六面体就称为单 元体。单元体的六个面上的应力表示过该点的法线方 向与坐标轴正向重合或相反的六个微元面上的应力。 根据作用力与反作用力相等的原理，单元体中相对表 面的应力矢量总是大小相等而方向相反的。
连续介质力学
连续介质力学的应用领域包括：工 程力学、流体力学、固体力学、生 物力学等。
连续性假设：假设介质是连续的没 有空隙或裂缝
各向同性假设：假设介质在各个方 向上都是相同的
添加标题
添加标题
添加标题
添加标题
均匀性假设：假设介质在各个方向 上都是均匀的
小变形假设：假设介质的变形很小 不会影响其物理性质
流体：不可压缩、连续、无固定形状的 物质如空气、水等
多尺度连续介质力学：研究不同尺度下的连续介质力学问题如分子动力学、介观力学等
跨学科连续介质力学：与其他学科交叉如生物力学、环境力学等
计算连续介质力学：发展高效的计算方法和软件解决复杂问题如流体动力学、固体力学 等
PRT SIX
连续介质力学是研究流体和固体力学 的重要学科
连续介质力学的特点包括：连续性、 守恒性、对称性等
研究方法：数学模型、数值 模拟、实验验证等
研究对象：连续介质如液体、 气体、固体等
基本概念：应力、应变、位 移、速度、加速度等
应用领域：工程力学、流体 力学、固体力学等
PRT THREE
弹性力学的定义：研究弹性体在外力作用下的变形和应力分布的学科 弹性力学的基本假设：连续性假设、小变形假设、均匀性假设、各向同性假设 弹性力学的基本方程：平衡方程、几何方程、物理方程 弹性力学的应用：工程结构设计、地震工程、材料科学等
,
汇报人：
CONTENTS
PRT ONE
PRT TWO
连续介质力学是研究连续介质（如 液体、气体、固体等）在力作用下 的变形、流动和应力分布的学科。
连续介质力学的研究内容包括：应 力、应变、变形、流动、热传导等。
添加标题
添加标题
添加标题
连续介质力学
b1
=
1 H1
g1
bi
=
1 Hi
gi
b2
=
1 H2
g2
b3
=
1 H3
g3
则 bi 为正交曲线坐标系的标准化正交基。
因此，显然有
ei
⋅ej
=
bi
⋅bj
= δij
=
⎧1 ⎨⎩0
i= j i≠ j
（2.1.4） （2.1.5）
质量守恒定律（非相对论，牛顿力学观点）； 能量守恒（热力学定律）； 有限变形及连续性条件（几何方程）。 2）材料本构方程 不同材料具有不同特性是材料属性，这属性称为本构属性。本构属性的描述为本构方 程。在本课程中，只讨论本构方程的框架（形式）。 具体本构方程只有通过实验得出，本构方程包含：①应力、应变关系；②材料常数。 本课程中，研究本构方程框架所应用的基本理论为： ① 基本连续介质热力学的内变量理论； ② 基于理性化公理的本构方程原理。 所得到的本构方程框架具有本构方程的指导原则。 非线性方面在下面两个方面反映： ① 有限变形—称为几何非线性。 ② 本构方程非线性—称为物理（材料）非线性。 若同时考虑以上两个方面的非线性因素，则称为双非线性问题。
2．空间的维数
设α i 为 m 个标量，若能选取α i ，使得
m
∑αiai = 0
i =1
（2.1.1）
且α i 不全为零，则称此 m 个矢量线性相关，否则，称为线性无关。
例 1 位于同一平面内的两个矢量 a1 和 a2 （如图
2.1.1）是线性无关的，即
a1
α1a1 + α2a2 ≠ 0 （α1 和α 2 可为任意值，
3．本课程的特点
① 普遍性； ② 严密性（只有一个基本假设，物理定律和公理作为依据）； ③ 溶入于连续介质热力学； ④ 对连续介质的本构方程作框架的理论研究。
连续介质力学-第2章-四川大学
0 0.36
10
4
0 Ω 3.22
3.22
0
10
4
B点
E
0.36
0
0 0.09
104
0 Ω 8.62
8.62
0
10
4
C点
0 E 0.11
0.11
0
10
4
0 Ω 6.64
6.64
0
pa
pa cos
pa
1
1
2!
2
L
pa
pa
dX 1
u1 X 1
dX 1 ,
12
u2 X 1
u1 X 2
2E12
pb
pb
dX 2
u 2 X 2
dX 2
u1 X 1
E
1 2
u1 X 2
X 1 x1
p
x2 X2
物质坐标：X
空间坐标：x
物质描述 （Lagrange 描述）
x xˆ ( X ,t) ˆ( X ,t)
空间描述 （Euler 描述）
X X(x,t)
ˆ(x, t)
x xˆ ( X ,t)
X X(x,t)
互逆
互为隐函数
x1 x1 x1
Lij vi , j
x点邻域的dv是x dx 处的速度对x点处的速度的偏离
加法分解 L D W
连续00连续介质的运动学
第二部分 连续介质力学第一章 连续介质的运动学物质是由原子和分子组成的。
因此，物质是不连续的。
但在日常生活中却有许多有关物质行为的外观现象，它们可以用不考虑物质分子结构的宏观理论来加以描述和预示。
例如，钢杆在已知力的作用下的伸长量，管道中水流的排出速度和物质在空气中运动所受到的阻力等等。
连续介质力学把物质看作是无限可分的,因此我们需要将物质的无限小体积看作是连续介质中的物质点或“粒子”。
1.1 连续介质的运动假设一个物体在某一瞬时(t t =0)占有物理空间V 0(充满物质的某一空间区域)。
在该瞬时物体中任一物质点P 的几何位置可以用由某一固定点O 引出的位置矢量X 来描述，而该物质点P 在任意瞬时t 的位置用位置矢量x 来表示(图1.1)。
因此，任何一个物质点的运动路线可由下列形式的方程描述：()t X x x ,= (1.11) 上式表示在初始0时刻占据位置X 的的物质在时刻t 的位置。
我们可以把方程看成是从空间区域V 0到V 的关于X 和x 的一一对应的连续变换。
它描述物体中任一物质的瞬时位置。
我们把对组成物质的全体物质点位置的完全刻画称为物体的构形(Configuration)。
另一方面，物体的运动也可由下列形式的方程描述：()t x X X ,= (1.12) 它表示在时刻t ，通过空间x 处的物质原来的初始位置。
如果在时刻t ，处于整个空间中每一物质点的原始位置都被给出，那么物体在t 时刻的构形也被完全地描述了。
若方程1.11和1.12描述同一运动过程，并且雅可比行列式 0det ≠⎥⎥⎦⎤⎢⎢⎣⎡=j i X x J ∂∂ (1.13)则式1.11和式1.12为互逆变换，且唯一。
在直角坐标系基矢量下()321,,e e e ,1.11式可以表示成x x e x e x e =++112233 (1.14) 于是方程具有下列分量形式: ()t X X X x x ,,,32111= ()t X X X x x ,,,32122=()t X X X x x ,,,32133= (1.15) 写成指标记法形式则为()t X X X x x i i ,,,321= (1.16) 同样地，方程1.12的指标记法形式为()t x x x X X i i ,,,321= (1.17)方程中X 是用来确定物体中的不同物质的，称之为物质坐标；而方程中的x 是用来确定物理空间中物体内各个物质点的空间位置的，因此我们称之为物质的空间坐标。
连续介质力学-例题与习题
《连续介质力学》例题和习题第一章 矢量和张量分析第一节 矢量与张量代数一、矢量代数令112233A A A =++A e e e ,112233B B B =++B e e e ,则有112233A A A αααα=++A e e e111222333()()()A B A B A B +=+++++A B e e e112233112233112233()()A A A B B B A B A B A B •=++•++=++A B e e e e e e112233112233111112121313212122222323313132323333()() A A A B B B A B A B A B A B A B A B A B A B A B ⨯=++⨯++=⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯A B e e e e e e e e e e e e e e e e e e e e e e e e又因为: 11⨯=e e 0;123⨯=e e e ;132⨯=-e e e ;213⨯=-e e e ;22⨯=e e 0;231⨯=e e e ; 312⨯=e e e ;321⨯=-e e e ;33⨯=e e 0则: 233213113212213(_)()()A B A B A B A B A B A B ⨯=+-+-A B e e e 习题:1、证明下列恒等式：1）[]2()()()()⨯•⨯⨯⨯=•⨯A B B C C A A B C2) [][]()()()()⨯•⨯=•⨯-•⨯A B C D A C D B B C D A2、请判断下列矢量是否线性无关？1232=-+A e e e 23=--B e e 12=-+C e e .其中i e 为单位正交基矢量。
3、试判断[]816549782-⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦A 是否有逆矩阵；如有，请求出其逆阵[]1-A 。
二、张量代数例1：令T 是一个张量，其使得矢量a ，b 经其变换后变为2=+Ta a b ，=-Tb a b ，假定一个矢量2=+c a b ，求Tc 。
《连续介质力学》课件
动量矩守恒定律
描述物质系统动量矩变化规律的定律。
动量矩守恒定律也是连续介质力学中的基本定律之一。它指出在一个没有外力矩作用的封闭系统中，系统的总动量矩保持不 变。动量矩是系统动量和位置矢量的乘积，因此这个定律说明系统的旋转运动状态只与系统的初始状态有关，而与时间无关 。
能量守恒定律
描述物质系统能量变化规律的定律。
金属材料的疲劳和断裂 研究
01
02
03
复合材料的细观结构和 力学行为分析
04
无损检测和结构健康监 测技术
环境科学
01
土壤和岩石的力学性质研究
02
地质工程和地震工程中的稳定性分析
03
生态系统和自然资源的可持续性发展研究
04
环境流体力学的模拟和分析
06
连续介质力学的未来发展
新材料与新结构的挑战
新材料特性
能量守恒定律是物理学中的基本定律之一，它在连续介质力学中也有重要应用。这个定律指出在一个 封闭系统中，系统的总能量保持不变。能量的形式可以包括动能、势能、内能等，但不论能量的形式 如何转化，总量始终保持不变。
熵增原理
描述系统无序程度变化规律的定律。
熵增原理是热力学中的基本定律之一，它指出在一个 封闭的热力学系统中，系统的熵（表示系统无序程度 的物理量）总是趋向于增加。也就是说，系统总是倾 向于向更加混乱和无序的状态发展，而不是向更加有 序和有组织的状态发展。这个原理在连续介质力学中 也有重要的应用，例如在研究流体和热传导等问题时 需要考虑熵增原理的影响。
THANKS
感谢观看
《连续介质力学》ppt课 件
• 连续介质力学概述 • 连续介质力学的基本概念 • 连续介质力学的物理定律 • 连续介质力学的数学模型 • 连续介质力学的应用领域 • 连续介质力学的未来发展
第一章2连续介质力学
⎡e1′ ⋅ e1 M = ⎢⎢e′2 ⋅ e1
⎢⎣e3′ ⋅ e1
e1′ ⋅ e2 e′2 ⋅ e2 e3′ ⋅ e2
e1′ ⋅ e3 ⎤ ⎡cos(e1′，e1 )
e′2
⋅
e3
⎥ ⎥
=
⎢⎢cos(e′2，e1
)
e3′ ⋅ e3 ⎥⎦ ⎢⎣cos(e3′，e1 )
cos(e1′，e2 ) cos(e′2，e2 ) cos(e3′，e2 )
A
A
A
J′ = MJMT
例1.26 证明： ∇v 是二阶张量。
解：
∇v
=
ei
∂ ∂xi
(v je j )
=
v j，i ei e j
xi = M mi xm′
∂xi ∂xm′
= M mi
vn′ = M nj v j
∂vn′ ∂xm′
= ∂vn′ ∂xi
∂xi ∂xm′
=
∂(Mnjvj ∂xi
)
Mmi
cos(e1′，e3 )⎤ cos(e′2，e3 )⎥⎥ cos(e3′，e3 )⎥⎦
b = (e1′ e′2 e3′ ) b′ = (e1 e2 e3 ) b b = (e1′ e′2 e3′ ) b′ = (e1 e2 e3 ) MT b′ = (e1 e2 e3 ) b
b = MTb′
b′ = Mb
定义：基矢量ei和ej可作并积，而形成二阶单位并矢量eiej
∇v = 2x1e1e1 + x2e1e2 + 4x2e2e1 + (x1 + 2x2 )e2e2
∇v = (e1
e2 )⎢⎣⎡42xx12
x2 ⎤ ⎡e1 ⎤
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
[a，b，c] [b，c，a] [c，a，b] [a，b，c] [b，a，c] [c，b，a] [a，c，b]
例:导出Kronecker符号与置换符号间的运算关系。
11 12 13 21 22 23 1 31 32 33
1i 1 j 1k ijk 2i 2 j 2k
(2) 数乘
a b (b j e j ) (b j )e j
(3) 数积
a b (ai ei ) (b j e j ) aibi a1b1 a2b2 a3b3
a b (ai ei ) (b j e j ) aibi a1b1 a2b2 a3b3
km kn kk
ijk mnk kkim jn jm kn ik kmin jk im kn jk kk jmin km jn ik 3im jn jm kn ik kmin jk im kn jk 3 jm in km jn ik 3im jn jm ni mjin im nj 3 jm in mi jn
➢矢量的旋度仍为矢量，是空间坐标点的函数
➢一点的旋度的大小是该点环量面密度的最大值。
➢旋度的方向是与该点最大环量面密度对应的法线方 向。
在矢量场中，若rot u＝J≠0，称之为旋度场(或涡旋场 )，J 称为旋度源(或涡旋源)，若矢量场处处rotu＝0 ，称之为无旋场。
小节：
梯度： grad u u
Einstein求和约定
哑标: 求和约定中的重复脚标
哑标可以用其它的字母代替，只要该字母在本项中 没有出现过就行
a aiei a je j
a jb j ck ambmck
哑标在同一项中只能重复一次
aibi ci
3
aibici
i 1
矢量的代数运算
(1) 加法
c a b aiei biei (ai bi )ei ciei
kk 3
kn ik ni
小结：
➢ Einstein求和约定 a ai ei
➢ Kronecker记号
ij
1 0
(i j) (i j)
➢ 置换符号
1
ijk 1
0
(当ijk是123的偶排列时) (当ijk是123的奇排列时) (当ijk有两个值相等时)
奇排列: 132，213，321
c a b (aiei ) (b j e j ) ijk aib j ek
ei e j ijk ek
ab ba
a b b a
(5) 混合积
[a，b，c] a (b c)
如果a、b、c的空间位置顺序服
(4) 矢积
c b a
c的模就是a和b所张成的平行四边形的面积
e1 e2 e3
c a b a1 a2 a3
b1 b2 b3
a1b2e3 a2b3e1 a3b1e2 a1b3e2 a2b1e3 a3b2e1
1. a、b和e的脚标一定是1、2、3的一个排列，在同一项内，不会重复出现1、2、 3中的任何一个数。
a b a b cos
1 ei e j 0
(i j) (i j)
ij
1 0
(i j) (i j)
Kronecker记号 ij
11 22 33 1
12 21 23 32 13 31 0
并积
散度： div u gu
数积
旋度： rot u u
矢积
( , , ) x1 x2 x 3
u (u1, u2 , u3)
矩阵：
▪ 方阵：行数＝列数； ▪ 矩阵的转置：将m×n的矩阵A的行列互换，得
到n×m的新矩阵，称作A的转置，记为AT； ≠ ▪ 列矩阵：只有一列的矩阵；
➢ 若div u > 0 则表示在该点处有“源”
➢ 若div u = 0 则表示在该点处无“源”无“汇”
➢ 其大小表示“源”和“汇”的强度
➢ 与坐标系无关
3. 旋度（rotation）
Stokes公式：
设 为分段光滑的空间有向闭曲线 , 是以 为边界的分片光滑的有向曲面, 的正向与的 法线符合右手规则 , 函数 P( x, y, z),Q( x, y, z) R( x, y, z)在包含曲面 在内的一个空间区域内
e1 e2 e3
令： rot u = u = x1 x2 x3
u1 u2 u3
物理意义：
旋度是用来描述一个旋涡源 (vortex source) 的 旋 涡 流 强 度 的 ， 而 所 谓 的 旋 涡 源 (vortex source)就是一个能在其周围造成一个“环”(即： 环量∮u.tdL) 的流源。因此为了描述此旋涡源 的強度，定义: 单位面积的最大环量称作旋度, 其方向为此环所为的面的法向量。
, 余子式： A1*n
A2*n
A21
An*n
Ai1
A22 L L Ai 2 L L
A2 j L L
Aij L L
A2 n Ain
An1 An2 L Anj L Ann
代数余子式： Ai*j =(-1)i+j余子式
关于转置和逆的计算规则:
转置: (A)T AT (A B)T AT BT
➢ 逆矩阵：对于方阵A，若存在方阵B，使AB = BA = I，则 称B是A的逆矩阵，记为B = A－1
逆矩阵存在的充要条件是|A|≠0
➢ 克莱默法则： A-1=A*/|A|
A11 A12 L A1 j L A1n
其中： 伴随矩阵A*
A1*1 A2*1
A1*2 L A2*2 L L
An*1 An*2 L
3i 3 j 3k
pi pj pk pqr ijk qi qj qk
ri rj rk
例1.5 证明 ijk mnk im jn in jm
im in ik ijk mnk jm jn jk
c
从右手螺旋法则，那么混合积的几
b
何意义就是由a、b、c所张成的平行
a
六面体的体积
三个矢量的混合积
[a，b，c] aiei (bje j ckek )
aiei jklbjckel jkl il aibjck jkiaibjck ijk aibjck
S
S
(v1dx2dx3 v2dx3dx1 v3dx1dx2 )
S
Gauss公式(奥高公式，或奥式公式)：
u n dS div u dV
S
V
通量
散度
divu
u
ui，i
u1 x1
u2 x2
u3 x3
物理意义:
➢ 若div u < 0 则表示在该点处有“汇”
▪ 行矩阵：列矩阵的转置；
a1
a
a2
M
an
A11 A12 L
A
A21
A22
L
L
An1 An2 L
A1n
A2n
Ann
▪ 对称矩阵：对于方阵A，有A=AT；
▪ 反对称矩阵：若AT =－A；
▪ 对角阵：方阵A的主对角线上有非零元素，其余元素均为零，
cos 2
x3
cos3
2. 散度（divergence）
v n dS vi nidS (v1cos1 v2cos2 v3cos3 )dS
S
S
S
称为矢量v在S上的通量
v n dS (v1cos1 v2cos2 v3cos3 )dS
置换符号 若数需次ijk要则交 是换偶01 奇排数列次。((当当则iijj该kk是有排1两2列3个的是值奇奇相排排等列列时时，))交换偶
方法二：
1
2
3
方法三 ：ijk 死 记jki 硬背 kij ijk jik ikj kji
偶排列: 123，231，312
n
曲线L的走向与n满足右手法则，
则根据Stokes公式，有：
L
Ñ ugtudLt dL
LL
=
S
( u3 x2
u2 x3
)dx2dx3
(u1 x3
u3 x1
)dx3dx1
( u
e1 e2 e3
dS S x1 x2 x3 u1 u2 u3
1.1 矢量、矩阵与张量
3
a a1e1 a2e2 a3e3 aiei i 1
a aiei
x3
e3
e2
e1
x2
x1 直角坐标系的基矢量
x3
a
a3
x2
x1
a1
a2
矢量的分量
在式子中的一项内，若出现了重复脚标，则表示该项关于这一
脚标对1、2、3求和，而勿须再写出求和记号
a aiei
2. 当a、b和e的脚标是123这个自然顺序的一个偶排列（即123，231，312）时， 该项取正号。
3. 当a、b和e的脚标是123这个自然顺序的一个奇排列（即132，213，321）时， 该项取负号。
偶排列与奇排列：
方法一： 123是偶排列；