明渠恒定非均匀流

在临界底坡上作均匀流时，满足临界流的条件式
Q
Ak g Bk
2
3
另一方面又要同时满足均匀流的基本方程式
Q Ak Ck Rk ik
联立可得临界底坡的计算式为
gAk g k ik 2 Ck Rk Bk Ck 2 Bk
一个坡度为i 的明渠，与其相应（即同流量、同 断面尺寸、同糙率）的临界底坡相比较可能有三种 情况： i i K 为缓坡
相应于断面单位能量最小值的水深称为临界水 深，以 hK 表示。 3 dEs Q2 AK 由临界流方程 0
dh g BK
当流量和过水断面形状及尺寸给定时，利用上式即 可求解临界水深 hK 。
可以用临界水深hk和实际水深h的大小，来判别流
态： 当 h hK 时，Fr 1 ，为缓流，
3、跃后长度的计算
Lh (2.5 ~ 3) Lj
（五）棱柱体水平明渠中水跃的能量损失计算 水跃的能量损失,以跃前断面的能量与跃后断面的 能量差作为水跃的消能量： 2 2 3 h） h (1 8Fr12 3) a1v1 a2v2 （h H j (h ) (h )= 2g 2g 4hh 16 (1 8Fr12 1)
v12 q2 Fr12 3 gh1 gh1
（四）棱柱体水平明渠水跃长度的计算 在水跃段内，水流紊动强烈，底部流速很大，一 般需设置护坦加以保护。此外，跃后段的一部分范 围内也需铺设海漫以免底部冲刷破坏。 1、矩形明渠的跃长的经验公式 欧拉-佛托斯基公式： L j 6.9(h h) Lj 10.3h(Fr1 1)0.81 切尔托乌索夫公式 吴春庭公式 Lj 9.4h( Fr1 1) 2、梯形断面跃长的经验公式 B1及B2为水跃前后断面处的水面宽度 B2 B1 L j 5h(1 4 ) B1
A、试算法
3 dEs Q2 AK 0 dh g BK
当给定流量Q及明渠断面形状、尺寸后，式的左端
aQ2 A3 g 为一定值，该式的右端 B 乃仅仅是水深的函数。
可以假定若干个水深h，从而可算出若干个与之对应
A3 B
的值，当某一
A3 B
aQ2 值刚好与 相等时，其相应的水 g
深即为所求的临界水深 hK 。
Fr
v v 2g = 2 h gh
2
佛汝德数的力学意义是： 代表水流的惯性力和重力两种作用的对比关系。（P138)
二、断面单位能量、临界水深 明渠中水流的流态也可从能量的角度来分析。 1、断面单位能量
如图所示渐变 流，若以0-0为 基准面，则过 水断面上单位 重量液体所具 有的总能量为
E z
水跃消能量与跃前断面水流的总能量的比值，称 为水跃消能率。
Kj H j H1 = (1 8Fr12 3)3 8 (1 8Fr12 1) 2+Fr12 ) （
Kj
Fr1
各种类型的水跃见图7-3
1 Fr1 1.7
，波状水跃，消能率很小；
1.7 Fr1 2.5 ，为弱水跃，紊动很弱，效能率<20%
横坐标，以
hK hK m ' hK ' 为纵坐标，画出 hK hK ' b
关曲线。
hK hK '
m hK b
当求解梯形断面临界水深时， 求出与梯形断面底宽相等的矩形断面的临界水深 hK 3
'
q2 g
根据梯形断面已知m , b值算出 m hK ' b
hK m ' h ~ hK 关系曲线上查出相应的 K ' 值， 由 ' b hK hK
（3）等腰梯形断面临界水深的计算
m 1 2 hK hK b ' m hK 1 hK b
1/ 3
m hK b
hK 3
'
q2 g
m ' m 现给定若干个 hK 值，则可得若干组对应的 b hK 和 b m ' hK m ' hK hK 和 ' 值，以 hK 为 ' 的值。利用这若干组对应的 b hK b hK
v 2
2g
z 0 h cos
v 2
2g
如果我们把参考基准面选在渠底这一特殊位置， 把对通过渠底的水平面 0' 0' 所计算得到的单位能量 称为断面比能，并以 E s 来表示
Es h cos h h
v
2
2g
v2
2g
Q
2
2 gA2
• 当流量Q和过水 断面的形状及尺 寸一定时，断面 比能仅仅是水深 的函数，即Es＝ f(h)，以图表示
水跃水力计算的主要内容有： (1) 共轭水深h1、h2的计算； (2) 水跃跃长的计算； (3) 水跃能量损失计算 。
（二）棱柱体水平明渠的水跃基本方程
1
根据断面1-1和2-2的动量方程和流量连续性方程， 可得到水跃方程：
Q2 Q2 A1hc1 A2 hc 2 gA1 gA2
当明渠断面的形状、尺寸以及渠中的流量一定时， 水跃方程的左右两边都仅是水深h的函数——水跃 函数： Q2
J ( h) gA Ahc
水跃方程也可记为：
J (h1 ) J (h2 )
上式表明，在棱柱体水平明渠中，跃前水深h1与跃后水深 h2具有相同的水跃函数值，两个水深为共轭水深。
水跃函数曲线： 与J(h)= min相应的水深即是临界水深
Q2 J ( h) Ahc gA
（三）棱柱体水平明渠共轭水深的计算
h1 q2 h2 1 8 3 1 2 gh1
或
h2 h1 2
q2 1 8 3 1 gh2
h2
h1 2
1 8Fr 1 或
2 1
h2 h1 1 8Fr22 1 2
2 v2 q2 Fr22 3 gh2 gh2
当 h hK 时，Fr 1 ，为临界流，
当 h hK 时，Fr 1 ，为急流。
（1）矩形断面明渠临界水深的计算
Q 为单宽流量。 b （2）断面为任意形状时，临界水深的计算 q
q2 hK 3 g
试算法
图解法
若明渠断面形状不规则，过水面积A与水深之间的 函数关系比较复杂，把这样的复杂函数代入条件式，不 能得出临界水深 hK 的直接解。在这种情况下，一般只能 用试算法或图解法求解 hK 。
B、图解法
3 dEs Q2 AK 0 dh g BK
图解法的实质和试算法相同。当假定不同的水深h时 A3 A3 ，可得出若干相应的 值，然后将这些值点绘成 h B B 关系曲线图（见图）
A3 在该图的 轴上，量取 B aQ2 其值为 的长度，由此引铅 g
垂线 hK 与曲线相交于C点，C 点所对应的h值即为所求
全国高职高专水利水电类精品规划教材
• 水力学课件

重庆电力高等专科学校
第七章
明渠恒定非均匀流
明渠水流的三种型态及其判别 缓流、急流的转换现象—水跌与水跃 明渠恒定非均匀渐变流基本方程 棱柱体渠道恒定非均匀渐变流水面线 分析 明渠恒定非均匀渐变流水面线分析 弯道水流简介
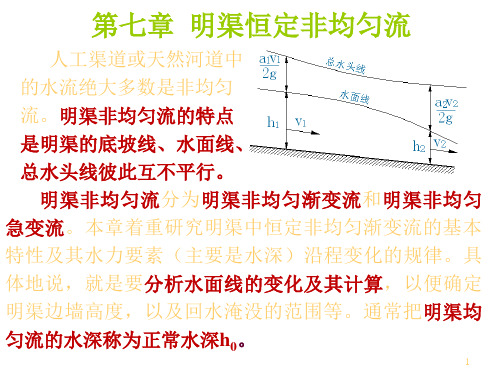
人工渠道或天然河道中的水流绝大多数是非均匀 流。 明渠非均匀流的特点是明渠的底坡线、水面线、 总水头线彼此互不平行。
v2 v2 ids dh cos ( )d( ) J f ds dh ( )d( ) J f ds 2g 2g Q2 其中，沿程损失坡降J f 2 K
s
0
在底坡为i的明渠渐变流中，沿水流方向任取一微 分流段 ds 。 对微分流段上、下游断面建立能量方程如下： 2 1v z0 h cos 2g
2 (v dv)2 ( z0 ids) (h dh) cos dh f dh j 2g 明渠恒定非均匀渐变流的基本微分方程式(1 2 )
2.5 Fr1 4.5 ，为摆动水跃，水跃不稳定，跃后水面
波动大，效能率<45%
4.5 Fr1 9.0 ，为稳定水跃，效能效率较45%~70%
建筑物下游消能，最好采用此范围。
Fr1 9.0
，为强水跃，跃后水面波动，而且下 游传播距离远。消能率>70%
例题7-4 例题7-5
7-3 明渠恒定非均匀渐变流基本方程 一、基本微分方程
从而可算出梯形断面的 hK 值。
三、临界底坡、缓坡与陡坡 到目前我们知道了三种水深： 均匀流正常水深 h 0 非均匀流水深 h 临界水深 hk 明渠均匀流的正常水深h0恰好与临界水深hk相等 时，此坡度定义为临界底坡。 若已知明渠断面形状及尺寸，当流量一定时，均 匀流情况下可将底坡与渠中正常水深的关系绘出。
（一）明渠中微波传播的相对波速
v vw gh (矩形断面）
v vw gh （任意断面）
（二）流态的判别数—佛汝德数Fr
v Fr vm
v v 2g = 2 h gh
2
当Fr＜1，水流为缓流； 当Fr＝1，水流为临界流； 当Fr＞1，水流为急流。
佛汝德数的物理意义是：
过水断面单位重量液体平均动能与平均势能之比的二倍 开平方。
（1）当缓坡渠道末端自由跌落时
上图所示的自由跌落是水跌的一个特例。跌落水 面必经过临界水深，但上坎缘处水深小于临界水深。
（2）当渠道底坡自缓坡变为陡坡时
hk
•渠道底坡由缓坡变为陡坡时，缓坡上游的均匀流为 缓流，水深大于临界水深。陡坡上的均匀流为急流， 水深小于临界水深。
• •
（3）当水流自水库进入陡坡渠道时 水库中水流为缓流，而陡坡渠道中均匀流为急流， 水流由缓流过渡到急流时，必经过临界水深。