2016建平中学自招数学答案
重点中学高中部自主招生数学考试试题(含答案)

2016年高中部自主招生考试试题数学(试题卷)一.选择题(共6小题,每小题6分,共36分)1.一列数a1,a2,a3,…,其中a1=,a n =(n为不小于2的整数),则a100=()A.B.2C.﹣1 D.﹣22.已知,则的值为()A.B.C.D.或13.已知AD∥BC,AB⊥AD,点E,点F分别在射线AD,射线BC上.若点E与点B关于AC对称,点E与点F 关于BD对称,AC与BD相交于点G,则()A.1+tan∠ADB=B.2BC=5CFC.∠AEB+22°=∠DEF D.4cos∠AGB=4.如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设a=1,则b=()A.B.C.D.5.如图所示,在直角坐标系中,A点坐标为(﹣3,﹣2),⊙A的半径为1,P为x轴上一动点,PQ切⊙A于点Q,则当PQ最小时,P点的坐标为()A.(﹣4,0)B.(﹣2,0) C.(﹣4,0)或(﹣2,0)D.(﹣3,0)6.已知抛物线y=﹣x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA()A.始终不相似B.始终相似C.只有AB=AD时相似D.无法确定二.填空题(共4小题,每小题6分,共24分)7.如果函数y=b的图象与函数y=x2﹣3|x﹣1|﹣4x﹣3的图象恰有三个交点,则b的可能值是.8.如图,已知直线交x轴、y轴于点A、B,⊙P的圆心从原点出发以每秒1个单位的速度向x轴正方向移动,移动时间为t(s),半径为,则t=s时⊙P与直线AB相切.9.一般地,我们把研究对象统称为元素,把一些元素组成的总体称为集合.一个给定集合中的元素是互不相同的,也就是说,集合中的元素是不重复出现的.如一组数1,1,2,3,4就可以构成一个集合,记为A={1,2,3,4}.类比实数有加法运算,集合也可以“相加”.定义:集合A与集合B中的所有元素组成的集合称为集合A与集合B的和,记为A+B.若A={﹣2,0,1,5,7},B={﹣3,0,1,3,5},则A+B=.10.对于X,Y定义一种新运算“*”:X*Y=aX+bY,其中a,b为常数,等式右边是通常的加法和乘法的运算.若成立,那么2*3=.三.解答题(共5题,每题12分,共60分)11.如图,二次函数与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位每秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动.设PQ交直线AC于点G.(1)求直线AC的解析式;(2)设△PQC的面积为S,求S关于t的函数解析式;(3)在y轴上找一点M,使△MAC和△MBC都是等腰三角形.直接写出所有满足条件的M点的坐标;(4)过点P作PE⊥AC,垂足为E,当P点运动时,线段EG的长度是否发生改变,请说明理由.试题图备用图12.已知直线y=﹣x+4与x轴和y轴分别交与B、A两点,另一直线经过点B和点D(11,6).(1)求AB、BD的长度,并证明△ABD是直角三角形;(2)在x轴上找点C,使△ACD是以AD为底边的等腰三角形,求出C点坐标;(3)一动点P速度为1个单位/秒,沿A﹣B﹣D运动到D点停止,另有一动点Q从D点出发,以相同的速度沿D ﹣B﹣A运动到A点停止,两点同时出发,PQ的长度为y(单位长),运动时间为t(秒),求y关于t的函数关系式.13.在边长为1的正方形ABCD中,以点A为圆心,AB为半径作圆,E是BC边上的一个动点(不运动至B,C),过点E作弧BD的切线EF,交CD于F,H是切点,过点E作EG⊥EF,交AB于点G,连接AE.(1)求证:△AGE是等腰三角形;(2)设BE=x,△BGE与△CEF的面积比,求y关于x的函数关系式,并写出自变量x的取值范围;(3)在BC边上(点B、C除外)是否存在一点E,使得GE=EF,若存在,求出此时BE的长,若不存在,请说明理由.14.如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3,MN=2.(1)求∠COB的度数;(2)求⊙O的半径R;(3)点F在⊙O上(是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.15.如图,直角梯形ABCO的两边OA,OC在坐标轴的正半轴上,BC∥x轴,OA=OC=4,以直线x=1为对称轴的抛物线过A,B,C三点.(1)求该抛物线的函数解析式;(2)已知直线l的解析式为y=x+m,它与x轴交于点G,在梯形ABCO的一边上取点P.①当m=0时,如图1,点P是抛物线对称轴与BC的交点,过点P作PH⊥直线l于点H,连结OP,试求△OPH 的面积;②当m=﹣3时,过点P分别作x轴、直线l的垂线,垂足为点E,F.是否存在这样的点P,使以P,E,F为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.2016年高中部自主招生考试数学参考答案选择题1-6.ABABDB填空题7.﹣6、﹣8.或249.{﹣3,﹣2,0,1,3,5,7}10.1解答题11.(1)y=﹣x2+2,x=0时,y=2,y=0时,x=±2,∴A(﹣2,0),B(2,0),C(0,2),设直线AC的解析式是y=kx+b,代入得:,解得:k=1,b=2,即直线AC的解析式是y=x+2;(2)当0<t<2时,OP=(2﹣t),QC=t,∴△PQC的面积为:S=(2﹣t)t=﹣t2+t,当2<t≤4时,OP=(t﹣2),QC=t,∴△PQC的面积为:S=(t﹣2)t=t2﹣t,∴;(3)当AC=CM=BC时,M的坐标是:(0,),(0,﹣2);当AM=BM=CM时,M的坐标是:(0,0),(0,);一共四个点,(0,),(0,0),(0,),(0,﹣2);(4)当0<t<2时,过G作GH⊥y轴,垂足为H.由AP=t,可得AE=.∵GH∥OP∴即=,解得GH=,所以GC=GH=.于是,GE=AC﹣AE﹣GC==.即GE的长度不变.当2<t≤4时,过G作GH⊥y轴,垂足为H.由AP=t,可得AE=.由即=,∴GH(2+t)=t(t﹣2)﹣(t﹣2)GH,∴GH(2+t)+(t﹣2)GH=t(t﹣2),∴2tGH=t(t﹣2),解得GH=,所以GC=GH=.于是,GE=AC﹣AE+GC=2﹣t+=,即GE的长度不变.综合得:当P点运动时,线段EG的长度不发生改变,为定值.12.(1)令x=0,y=4,令y=0,则﹣x+4=0,解得x=3,所以,A(0,4),B(3,0),由勾股定理得,AB==5,BD==10,过点D作DH⊥y轴于H,DH=11,AH=2,由勾股定理得,AD===,∵AB2=25,BD2=100,∴AB2+BD2=AD2,∴△ABD是直角三角形;(2)设OC长为x,由等腰三角形以及勾股定理得到x2+42=(11﹣x)2+62,解得x=,所以,C(,0);(3)设t秒时相遇,由题意得,t+t=5+10,解得t=7.5,点P在AB上时,0≤t≤5,PB=5﹣t,BQ=10﹣t,PQ===,点P、Q都在BD上重合前,5<t≤7.5,PQ=5+10﹣t﹣t=15﹣2t,重合后,7.5<t≤10,PQ=t+t﹣5﹣10=2t﹣15,点Q在AB上时,10<t≤15,PB=t﹣5,BQ=t﹣10,PQ===.13.(1)连AH,∵AH⊥EF,GE⊥EF,∴GE∥AH,∴∠GEA=∠EAH,∵AH=AB,AE=AE,∠ABE=∠AHB,∴△AHE≌△ABE,∴∠BAE=∠EAH,∴∠BAE=∠GEA,∴AG=EG,即△AGE是等腰三角形.(2)∵EH=EB=x,∴EC=1﹣x,CF=1﹣FD,∵FD=FH,∴EF=EH+HF=x+FD,在Rt△ECF中,EF2=EC2+CF2,∴(1﹣x)2+(1﹣FD)2=(x+FD)2,整理得,(1+x)FD=1﹣x,∴,∵∠B=∠C,又GE⊥EF,∴∠GEB=∠FEC,∴△GEB∽△EFC,∴,∴,∴(0<x<1).(3)假设BC上存在一点E,能使GE=EF,则,∴,解得x=0或x=1,经检验x=0或x=1是原方程的解但动点E不能与B,C点重合,故x≠0且x≠1,∴BC边上符合条件的E点不存在.14.(1)∵AE切⊙O于点E,∴AE⊥CE,又OB⊥AT,∴∠AEC=∠CBO=90°,又∠BCO=∠ACE,∴△AEC∽△OBC,又∠A=30°,∴∠COB=∠A=30°;(2)∵AE=3,∠A=30°,∴在Rt△AEC中,tanA=tan30°=,即EC=AEtan30°=3,∵OB⊥MN,∴B为MN的中点,又MN=2,∴MB=MN=,连接OM,在△MOB中,OM=R,MB=,∴OB==,在△COB中,∠BOC=30°,∵cos∠BOC=cos30°==,∴BO=OC,∴OC=OB=,又OC+EC=OM=R,∴R=+3,整理得:R2+18R﹣115=0,即(R+23)(R﹣5)=0,解得:R=﹣23(舍去)或R=5,则R=5;(3)以EF为斜边,有两种情况,以EF为直角边,有四种情况,所以六种,画直径FG,连接EG,延长EO与圆交于点D,连接DF,如图所示:∵EF=5,直径ED=10,可得出∠FDE=30°,∴FD=5,则C△EFD=5+10+5=15+5,由(2)可得C△COB=3+,∴C△EFD:C△COB=(15+5):(3+)=5:1.∵EF=5,直径FG=10,可得出∠FGE=30°,∴EG=5,则C△EFG=5+10+5=15+5,∴C△EFG:C△COB=(15+5):(3+)=5:1.15.(1)由题意得:A(4,0),C(0,4),对称轴为x=1.设抛物线的解析式为y=ax2+bx+c,则有:,解得.∴抛物线的函数解析式为:y=﹣x2+x+4.(2)①当m=0时,直线l:y=x.∵抛物线对称轴为x=1,∴CP=1.如答图1,延长HP交y轴于点M,则△OMH、△CMP均为等腰直角三角形.∴CM=CP=1,∴OM=OC+CM=5.S△OPH=S△OMH﹣S△OMP=(OM)2﹣OM•CP=×(×5)2﹣×5×1=﹣=,∴S△OPH=.②当m=﹣3时,直线l:y=x﹣3.设直线l与x轴、y轴交于点G、点D,则G(3,0),D(0,﹣3).假设存在满足条件的点P.a)当点P在OC边上时,如答图2﹣1所示,此时点E与点O重合.设PE=a(0<a≤4),则PD=3+a,PF=PD=(3+a).过点F作FN⊥y轴于点N,则FN=PN=PF,∴EN=|PN﹣PE|=|PF﹣PE|.在Rt△EFN中,由勾股定理得:EF==.若PE=PF,则:a=(3+a),解得a=3(+1)>4,故此种情形不存在;若PF=EF,则:PF=,整理得PE=PF,即a=3+a,不成立,故此种情形不存在;若PE=EF,则:PE=,整理得PF=PE,即(3+a)=a,解得a=3.∴P1(0,3).b)当点P在BC边上时,如答图2﹣2所示,此时PE=4.若PE=PF,则点P为∠OGD的角平分线与BC的交点,有GE=GF,过点F分别作FH⊥PE于点H,FK⊥x轴于点K,∵∠OGD=135°,∴∠EPF=45°,即△PHF为等腰直角三角形,设GE=GF=t,则GK=FK=EH=t,∴PH=HF=EK=EG+GK=t+t,∴PE=PH+EH=t+t+t=4,解得t=4﹣4,则OE=3﹣t=7﹣4,∴P2(7﹣4,4)c)∵A(4,0),B(2,4),∴可求得直线AB解析式为:y=﹣2x+8;联立y=﹣2x+8与y=x﹣3,解得x=,y=.设直线BA与直线l交于点K,则K(,).当点P在线段BK上时,如答图2﹣3所示.设P(a,8﹣2a)(2≤a≤),则Q(a,a﹣3),∴PE=8﹣2a,PQ=11﹣3a,∴PF=(11﹣3a).与a)同理,可求得:EF=.若PE=PF,则8﹣2a=(11﹣3a),解得a=1﹣2<0,故此种情形不存在;若PF=EF,则PF=,整理得PE=PF,即8﹣2a=•(11﹣3a),解得a=3,符合条件,此时P3(3,2);若PE=EF,则PE=,整理得PF=PE,即(11﹣3a)=(8﹣2a),解得a=5>,故此种情形不存在.d)当点P在线段KA上时,如答图2﹣4所示.∵PE、PF夹角为135°,∴只可能是PE=PF成立.∴点P在∠KGA的平分线上.设此角平分线与y轴交于点M,过点M作MN⊥直线l于点N,则OM=MN,MD=MN,由OD=OM+MD=3,可求得M(0,3﹣3).又因为G(3,0),可求得直线MG的解析式为:y=(﹣1)x+3﹣3.联立直线MG:y=(﹣1)x+3﹣3与直线AB:y=﹣2x+8,可求得:P4(1+2,6﹣4).e)当点P在OA边上时,此时PE=0,等腰三角形不存在.综上所述,存在满足条件的点P,点P坐标为:(0,3)、(3,2)、(7﹣4,4)、(1+2,6﹣4).。
建平中学自招真题解析

同理可得高一(2) (2)共 69 人,高一(1) (3)共 65 人.
14. 如图,在平面直角坐标系中,点 A 4,0 ,以 OA 为直径在 第一象限作半圆 C , 点 B 是该半圆周上一动点, 连结 OB 、
上
因此高一(1) , (2) , (3)班各有 30,34,35 人.
海
昂
x y 64 x 30 因此设高一(1) , (2) , (3)班各有 x, y, z 人可列方程组 y z 69 ,解得 y 34 . z x 65 z 35
2
分别对应 a 0, a 3, 0 a 3 的情况. 若 x 0 时取最小值,则 a 2 符合条件; 若 x 3 时取最小值,则 a 2.2 不符合条件. ; 若 x a 时取最小值,则 a a 2 2 ,解得 a 2, 1 ,其中 a 2 符合条件. 因此 a 2 或 2 .
sin DAE
DP AP
DP AD 2 DP 2
5 2 5 52 2
2
C
5 , 5
所以 DE 2
11. 如图,在梯型 ABCD 中, AB // CD , AC 、 BD 相交于点 O ,若 AC 6 , BD 8 ,中
内
【答案】 2 6 . 【解析】因为 AB // CD , 所以
【解析】原式
2 3 2
3
7 13 7
13
2 3 2 3
2 3
3 2 2 6 5.
5.
建平中学社团活动丰富多彩,有 JTV 社(金苹果电视台) 、04 辩论社、智能机器人社、 健美操社……,在一次社团文化节上,中国象棋社开展了社员 PK 活动,每个选手和其 他选手比赛一局,每局赢者得 2 分,输者得 0 分,平各记 1 分,现有四位同学统计了比 学只有一位同学统计正确,则这次比赛中有 名选手参加比赛. 赛中全部选手得分总数,总分分别是 1054、1056、1060、1066,经核实,上述四位同
建平中学自招真题含解析

y
y
y
y 99
y 99
所以 x 1 10x 1 2019 10 2009 .
y
y 99 99 99
4. 计算: 14 26 21 39
.
14 26 21 39
【答案】 2 6 5 .
2 3 【解析】原式
7 13
2 3
2 3
3 2 2 65.
2 3 7 13 2 3
将120 从十进制转换为15 进制可得结果为80 .
2. 如果 x 1 x4 1成立,那么满足它的所有整数 x 的值是
.
【答案】 2, 4 .
【解析】若 x 1x4 1,则 x 1 1或 x 4 0 且 x 1 0 . 因此 x 2 或 x 4 .
3. 设实数 x 、 y 分别满足 99x2 2019x 1 0 、 y2 2019 y 99 0 ,并且 xy 1 ,则
5. 建平中学社团活动丰富多彩,有 JTV 社(金苹果电视台)、04 辩论社、智能机器人社、
健美操社……,在一次社团文化节上,中国象棋社开展了社员 PK 活动,每个选手和其
他选手比赛一局,每局赢者得 2 分,输者得 0 分,平各记 1 分,现有四位同学统计了比
赛中全部选手得分总数,总分分别是 1054、1056、1060、1066,经核实,上述四位同
验证可知只有 x x 1 1056 有整数解 x 33 ,因此共有 33 名选手参赛.
6. 二次函数 y x2 2ax a 在 0 x 3 上有最小值 2 ,则 a 的值为
.
【答案】 2 或 2 .
【解析】二次函数 y x2 2ax a 在 0 x 3 上的最小值在 x 0 或 x 3 或 x a 时取到,
(中考)自主招生考试数学试题与答案(201605202013)

自主招生考试数学试题第Ⅰ卷(选择题,共36分)一、选择题(本大题共12个小题,每小题3分,共36分.每小题给出的四个选项中,只有一个符合题目的要求)1.4-的相反数是 ( )A.14-B.14 C.4 D.4-2.科技城2012年国民生产总值约为14000000万元,用科学记数法表示为 ( ) A.71410⨯ B.71.410⨯C.61.410⨯ D.70.1410⨯3.一次数学测试后,随机抽取九年级某班5名学生的成绩如下:91,78,98,85, 98.关于这组数据说法错误的是( )A.平均数是91 B.极差是20 C.中位数是91 D.众数是984.在一个不透明的盒子中装有3个红球、2个黄球和1个绿球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到黄球的概率为()A.12 B.13 C.16 D.15.已知x是实数,且(2)(3)10x x x---=,则x2+x+1的值为()A.13 B. 7 C. 3 D. 13或7或36. 如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则sin C等于 ( )A.34 B.43 C.45 D.357.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是 ( )A.点(0,3) B.点(2,3) C.点(6,1) D.点(5,1)8.将抛物线23xy=向左平移2个单位,再向下平移1个单位,所得抛物线为()A.23(2)1y x=-+ B.23(2)1y x=+-C.23(2)1y x=-- D.23(2)1y x=++9.图中各图是在同一直角坐标系,二次函数y=ax2+(a-c)x+c与一次函数y ax c=+的大致图象,有且只有一个是正确的,正确的是 ( )10. 如图O⊙是ABC△的外接圆,AD是O⊙的直径,O⊙半径为23,2AC=,则sin B为()A .23B .32C .34D .4311.如图,在矩形ABCD 中,AB=2,BC=4.将矩形ABCD 绕点C 沿顺时针方向旋转90°后,得到矩形FGCE (点A 、B 、D 的对应点分别为点F 、G 、E ).动点P 从点B 开始沿BC-CE 运动到点E 后停止,动点Q 从点E 开始沿EF-FG 运动到点G 后停止,这两点的运动速度均为每秒1个单位.若点P 和点Q 同时开始运动,运动时间为x (秒),∆APQ 的面积为y ,则能够正确反映y 与x 之间的函数关系的图象大致是( )A B C D12. 如图,在ABC ∆中,5==AC AB ,8=CB ,分别以AB 、AC 为直径作半圆,则图中阴影部分面积是 ( )A .25244π-B .2524π-C .2512π-D .25124π-第Ⅱ卷(非选择题,共114分)二、填空题(本大题共6个小题,每小题4分,共24分.请将答案填入答题卡相应的横线上.) 13.函数2y x =-x 的取值围是 .14.分解因式:3244a a a -+= . 15.已知⊙O 1与⊙O 2的半径分别是方程28150x x -+=的两根,且两圆的圆心距122O O t =+,若这两个圆相交,则t 的取值围为 .16. 在平面直角坐标系xOy 中,有一只电子青蛙在点A(1,0)处.第一次,它从点A 先向右跳跃1个单位,再向上跳跃1个单位到达点A 1;第二次,它从点A 1先向左跳跃2个单位,再向下跳跃2个单位到达点A 2;第三次,它从点A 2先向右跳跃3个单位,再向上跳跃3个单位到达点A 3;第四次,它从点A 3先向左跳跃4个单位,再向下跳跃4个单位到达点A 4;……依此规律进行,点7A的坐标为 ;若点A n 的坐标为(2014,2013),则n= .17. 如图,PA 与⊙O 相切于点A ,PO 的延长线与⊙O 交于点C ,若⊙O 的半径为3,PA=4.弦AC 的长为 .18. 在直角梯形ABCD 中,AD BC ∥,90ABC AB BC E ∠==°,,为AB 边上一点,15BCE ∠=°,且AE AD =.连接DE 交对角线AC 于H ,连接BH .下列结论:①ACD ACE △≌△; ②CDE △为第12题图A CB O 第10题图 第11题图第17题P BO CA绵阳市2008-2012年农业观光园 经营年收入统计图 绵阳市2009-2012年农业观光园 经营年收入增长率统计表 等边三角形; ③2EH BE =; ④EBC EHCS AH S CH =△△.其中结论正确的是( )三、解答题(本大题共7个小题,共90分.解答应写出文字说明、证明过程或演算步骤) 19.(本题共2个小题,每小题8分,共16分)(1)计算:0112(31)2sin 603-+--︒+.(2)先化简,后计算: ,其中33a =-.20.(本小题满分12分)近年来,郊区依托丰富的自然和人文资源,大力开发建设以农业观光园为主体的多类型休闲旅游项目,城郊旅游业迅速崛起,农民的收入逐步提高.以下是根据市统计局2013年1月发布的“市主要经济社会发展指标”的相关数据绘制的统计图表的一部分.请根据以上信息解答下列问题:(1) 市2010年农业观光园经营年收入的年增长率 是 ;(结果精确到1%) (2) 请补全条形统计图并在图中标明相应数据;(结果精确到0.1)(3) 如果从2012年以后,市农业观光园经营年收入都按30%的年增长率增长,请你估算,若经营年收入要不低于2008年的4倍,至少要到 年(填写年份).21. (本小题满分12分)如图,已知等腰直角△ABC 中,∠BAC=︒90,圆心O 在△ABC 部,且⊙O 经过B 、C 两点,若BC=8,AO=1,求⊙O 的半径.年份 年增长率(精确到1%)2009年 12% 2010年 2011年 22% 2012年 24%第18题图22.(本小题满分12分)某科技开发公司研制出一种新型产品,每件产品的成本为2300元,销售单价定为3000元.在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2500元. (1)商家一次购买这种产品多少件时,销售单价恰好为2500元?(2)设商家一次购买这种产品x 件,开发公司所获得的利润为y 元,求y (元)与x (件)之间的函数关系式,并写出自变量x 的取值围. 23.(本小题满分12分)如图,在△ABC 中,AB=AC ,以A C 为直径作⊙O 交BC 于点D ,过点D 作FE ⊥AB于点E ,交AC 的延长线于点F .(2) 若AE=6,sin∠CF D=35,求EB 的长.24. (本小题满分12分)如图,AB 为⊙O 的直径,AB=4,P 为AB 上一点,过点P 作⊙O 的弦CD ,设∠BCD=m∠ACD.(1)已知221+=m m ,求m 的值,及∠BCD、∠ACD 的度数各是多少?第23题图(2)在(1)的条件下,且21=PB AP ,求弦CD 的长; (3)当323-2+=PB AP 时,是否存在正实数m ,使弦CD 最短?如果存在,求出m 的值,如果不存在,说明理由.25. (本小题满分14分)如图1,在平面直角坐标系xOy 中,直线l :34y x m =+与x 轴、y 轴分别交于点A 和点B(0,32-),抛物线234y x bx c =++经过点B ,且与直线l 的另一个交点为C9(,)4n . (1) 求n 的值和抛物线的解析式;(2) 点D 在抛物线上,且点D 的横坐标为(0)t t n <<.DE∥y 轴交直线l 于点E ,点F 在直线l 上,且四边形DFEG 为矩形(如图2).若矩形DFEG 的周长为p ,求p 与t 的函数关系式以及p 的最大值; (3) M 是平面一点,将△AOB 绕点M 沿逆时针方向旋转90°后,得到△A 1O 1B 1,点A 、O 、B 的对应点分别是点A 1、O 1、B 1.若△A 1O 1B 1的两个顶点恰好落在抛物线上,请求出点A 1的横坐标.(答案 D AA D二、填空题(本大题共6个小题,每小题4分,共24分) 13. 14. 2(2)a a - 15. 16.(5,4),4025 17.12518..(1)(2)(4)三19.(本题共2个小题,每小题8分,共16分)(1)解:原式31423123233+-⨯+=+. ………………………8分(2)原式= …………………5分当33a =-时,原式233=. …………………………………8分20. (1)17%; ……………………………4分 (2)所补数据为21.7; ……………………6分补全统计图如图20; …………………8分(3)2015. …………………………12分 21. 解:联结BO 、CO ,联结AO 并延长交BC 于D …1分 ∵等腰直角三角形ABC 且∠BAC=︒90 ∴ AB=AC ……2分 ∵ O 是圆心 ∴OB=OC∴直线OA 是线段BC 的垂直平分线 …4分 ∴ AD⊥BC,且D 是BC 的中点 ……………6分在Rt△ABC 中,AD=BD=BC21∵BC=8 BD=AD = 4 ……………8分 ∵AO=1 ∴OD=BD -AO=3 ……………10分∵AD⊥BC ∴∠BDO=︒90 ∴OB=5432222=+=+BD OD ……12分22. 解:(1)设商家一次购买该种产品x 件时,销售单价恰好为2500元,依题意得300010(10)2500x --=,解得60x =. ………………………………3分答:商家一次购买该种产品60件时,销售单价恰好为2500元. ………… 4分 (2)当010x ≤≤时,(30002300)700y x x =-=; ……………… 6分当1060x <≤时,[]2300010(10)230010800y x x x x =---=-+; …… 8分当60x >时,(25002300)200y x x =-= . ……………………10分所以,()()()⎪⎩⎪⎨⎧∈>∈≤<+-∈≤≤=Z x x x Z x x x x Z x x x y ,60,200,6010,80010,100,7002……………………12分23. (1)证明:连接OD . ∵OC=OD,∴∠OCD=∠ODC. ………1分 ∵AB=AC,∴∠ACB=∠B. ………2分∴∠ODC=∠B.∴OD∥AB. …………………………… 3分 ∴∠ODF=∠AEF. ………4分 ∵EF⊥AB,图20CBOA 第21题∴∠ODF =∠AEF =90°. ………5分∴OD⊥EF . ∵OD 为⊙O 的半径,∴EF 与⊙O 相切. ……6分 (2)解:由(1)知:OD∥AB,OD⊥EF .在Rt △AEF 中,sin∠CFD = AE AF = 35,AE=6.∴AF=10. ……8分∵OD∥AB,∴△ODF∽△AEF.∴AE ODAF OF =. ………9分 设⊙O 的半径为r ,∴10-r 10 = r6.解得r= 154. …………………………10分∴AB= AC=2r = 152 . ∴EB=AB -AE= 152 -6= 32. …… ………… 12 分24.解:(1)由221+=m m ,得 2=m . …………………………1分连结AD 、BD. ∵AB 是⊙O 的直径∴∠ACB=90°,∠ADB=90°, 又∵∠BCD=2∠ACD,∠ACB=∠BCD+∠ACD.∴∠ACD=30°,∠BCD=60°. ……………………2分 (2)连结AD 、BD ,则∠ABD=∠ACD=30°,AB=4, ∴AD=2,32=BD . ……3分∵21=PB AP ,∴34=AP ,38=BP . …………4分 ∵∠APC=∠DPB,∠ACD=∠ABD.∴△APC∽△DPB …………………5分∴BP PCDP AP DB AC ==, ∴3383234=⋅=⋅=⋅DB AP DP AC ①,4832339PC DP AP BP ⋅=⋅=⋅=②同理△CPB∽△APD ……………………6分∴AD BC DP BP =,∴316238=⋅=⋅=⋅AD BP DP BC ③, 由①得DP AC 338=,由③得16,3BC DP=23316338==::BC AC , 在△ABC 中,AB=4,∴2224)316()338=+DP DP (,∴372=DP.由②329PC DP PC ⋅==,得PC =.∴DC CP PD =+=+=. ……………………8分方法二由①÷③得23316338==::BC AC ,在△ABC 中,AB=4,72143774=⋅=AC ,7782774=⋅=BC . 由③316778=⋅=⋅DP DP BC ,得372=DP .由②329PC DP PC ⋅==,得PC =.∴DC CP PD =+=+=. ……………………8分(3)连结OD ,由323-2+=PBAP ,AB =4, 则323-24+=-AP AP ,则AP AP )()(3-2)32(432--=+, 则32-=AP .32=-=AP OP . ……………………10分要使CD 最短,则CD⊥AB 于P ,于是23cos ==∠OD OP POD .︒=∠30POD ,∴∠ACD=15°,∠BCD=75°,∴m=5,故存在这样的m 值,且m=5. ……………12分25.解:解:(1)∵直线l :34y x m=+经过点B (0,32-),∴32m =-.∴直线l 的解析式为3342y x =-.∵直线l :3342y x =-经过点9(,)4c n , ∴933,442n =-解得5n = .………………………1分 ∵抛物线234y x bx c=++经过点9(,)4c n 和点B (0,32-),23,29355.44c b c ⎧=-⎪⎪∴⎨⎪=⨯++⎪⎩解得3,3.2b c =-⎧⎪⎨=-⎪⎩ ……………2分∴抛物线的解析式为233342y x x =--. ……………3分(2)∵直线l :3342y x =-与x 轴交于点A ,∴点A 的坐标为(2,0).∴OA=2.在Rt△OAB 中,OB=32,22OA OB +22352()22+=. ……………5分∵DE∥y 轴,∴∠OBA=∠FED.∵矩形DFEG 中,∠DFE=90°, ∴∠DFE=∠AOB=90°.∴△OAB∽△FDE . ………6分∴OA OB ABFD FE DE ==. ∴45OA FD DE DE AB =⋅=,35OB FE DE DE AB =⋅=. ……………………7分FG yxO BADC El图25∴p =2(FD+ FE)=43142()555DE DE⨯+=.∵D(t ,233342t t --),E (t ,3342t -),且05t <<, ∴223333315()(3)424244DE t t t t t=----=-+. ∴22143152121()544102p t t t t =⨯-+=-+. ∵2215105()1028p t =--+,且21010-<,∴当52t =时,p 有最大值1058…………………………9分(3)根据题意可得11O B 与x 轴平行,11O A 与y 轴平行.1)当11,O B 在抛物线上时,根据条件可设11113(,),(,)2O t y B t y +,则223333333()3()424222t t t t --=+-+-,解得54t =. …………11分 2)当11,A B 在抛物线上时,根据条件可设11113(,),(,2)2A t y B t y +-,则223333333()3()2424222t t t t --=+-+-+,解得1336t =. .……13分 综上,点A 1的横坐标为54或1336. .……14分。
上海中考自招真题26套及其答案

四校八大历年自招真题答案目录2013年上中自招试卷2014年上中自招试卷2015年上中自招试卷2011年华二自招试卷2012年华二自招试卷2014年华二自招试卷2013年华二冬令营数学试卷2015年年华二自招试卷2017年年华二自招试卷2013年复附自招试题2014年复附自招试题一2014年复附自招试题二2015年复附自招试题一2015年复附自招试题二2012年交附自招试题2013年交附自招试题2014年交附自招试题2015年交附自招试题2016年交附自招试题2014年七宝自招试题2016年七宝自招试题2016年南模自招试题2016年建平自招试题2017年建平自招试题建平数学培训资料试卷2015年控江自招试题2013年华二冬令营数学试卷1、“帽子函数”的图像如图所示:(1)求此函数的解析式;(2)若有抛物线23(),4y x a a =-+<求它与“帽子函数”图像的交点个数; (3)请试写出一个抛物线解析式,使它与“帽子函数”图像有且只有2个交点,横坐标分别为5722,.【解析】:⑴1,211,12x k x k y x k k x k ⎧≤<+⎪⎪=⎨⎪-+++≤<+⎪⎩⑵0a <时,无交点0a =时,一个交点304a <<时,两个交点 ⑶考虑到34a =时,抛物线234y x =-+与帽子函数交于11,22⎛⎫- ⎪⎝⎭、11,22⎛⎫ ⎪⎝⎭两点, 所以可以将234y x =-+向右平移3个单位,即满足条件 该抛物线解析式为()2334y x =--+2、在一个8×8的正方形方格纸中,一个角剪去一个2×2的小正方形,问其余部分可否剪成15块“L ”型(如图)纸片,若能剪,给出剪切方法,若不能剪,请说明理由。
【解析】(一道基础的染色问题)如图进行黑白相间染色,那么L 型放入方格纸中,必定可以盖住1个黑格子和3个白格子,或者3个黑格子和1个白格子。
建平中学2016-2017学年高二下学期期中数学试卷 含解析

2016-2017学年上海市建平中学高二(下)期中数学试卷一。
填空题1.设复数z=3+4i(i是虚数单位),则•z=.2.已知复数为纯虚数(i是虚数单位),则实数a= .3.已知点A、B到平面α的距离分别是4、6,则线段AB的中点M 到平面的距离α是.4.如图,正方体ABCD﹣A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于.5.二面角α﹣l﹣β为60°,异面直线a、b分别垂直于α、β,则a与b所成角的大小是.6.已知A是△BCD所在平面外一点,E、F分别是BC和AD的中点,若BD⊥AC,BD=AC,则EF与BD所成角的大小是.7.双曲线3y2﹣x2=1的两条渐近线的夹角是.8.已知椭圆C:,点M与C的焦点不重合,若M关于C的焦点的对称点分别为A,B,线段MN的中点在C上,则|AN|+|BN|= .9.已知复数z满足|z+2﹣i|=1,则|2z﹣1|的取值范围是.10.设实系数一元二次ax2+bx+c=0的两根是x1、x2,下列命题中,假命题的序号是(1)方程可能有两个相等的虚根(2)ax2+bx+c=(x﹣x1)(x﹣x2)(3)(4)若b2﹣4ac<0,则x1﹣x2一定是纯虚数.11.定长是3的线段AB的两端点在抛物线y2=x上移动,M是线段AB的中点,则M到y轴距离的最小值是.12.斜率是1的直线与椭圆交于A、B两点,P为线段AB上的点,且AP=2PB,则点P的轨迹方程是.二.选择题13.下列几何体中,多面体是()A.B.C.D.14.一条直线和该直线外不共线的三点最多可以确定平面的个数为()A.1个B.3个 C.4个 D.6个15.下列命题中,假命题的个数是()(1)若直线a在平面α上,直线b不在平面α上,则a、b是异面直线(2)若a、b是异面直线,则与a、b都垂直的直线有且只有一条(3)若a、b是异面直线,则与c、d与直线a、b都相交,则c、d 也是异面直线(4)设a、b是两条直线,若a∥平面α,a∥b,则b∥平面αA.1个B.2个 C.3个 D.4个16.已知圆F的方程是x2+y2﹣2y=0,抛物线的顶点在原点,焦点是圆心F,过F引倾斜角为α的直线l,l与抛物线和圆依次交于A、B、C、D四点(在直线l上,这四个点从左至右依次为A、B、C、D),若|AB|,|BC|,|CD|成等差数列,则α的值为( )A.±arctan B .C.arctan D.arctan或π﹣arctan三.简答题17.实数x取什么值时,复数z=(x2﹣2x﹣3)+(x2+3x+2)i(i为虚数单位);(1)是实数?(2)对应的点位于复平面的第二象限?18.在长方体ABCD﹣A1B1C1D1中,AA1=AD=2,AB=4;(1)求证:AD1⊥平面A1B1D;(2)求BD与平面ACC1A1所成角的大小.19.某乳业公司生产甲、乙两种产品,需要A、B、C三种苜蓿草饲料,生产1个单位甲种产品和生产1个单位乙种产品所需三种苜蓿草饲料的吨数如表所示:产品苜蓿草A B C饲料甲483乙5510现有A种饲料200吨,B种饲料360吨,C种饲料300吨,在此基础上生产甲乙两种产品,已知生产1个单位甲产品,产生的利润为2万元,生产1个单位乙产品,产生的利润为3万元,分别用x、y表示生产甲、乙两种产品的数量;(1)用x、y列出满足生产条件的数学关系式,并画出相应的平面区域;(2)问分别生产甲乙两种产品多少时,能够产出最大的利润?并求出此最大利润.20.已知下列两个命题:命题p:实系数一元二次方程x2+mx+2=0有虚根;命题q:关于x的方程:2x2﹣4(m﹣1)x+m2+7=0(m∈R)的两个虚根的模的和不大于,若p、q均为真命题,求实数m的取值范围.21.已知椭圆左、右焦点分别为F1、F2,点p为直线l:x+y=2上且不在x轴上的任意一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D,O为坐标原点;(1)求△ABF2的周长;(2)设直线PF1、PF2的斜率分别为k1、k2,证明:;(3)问直线l是否存在点P,使得直线OA、OB、OC、OD的斜率k OA、k OB、k OC、k OD满足k OA+k OB+k OC+k OD=0?若存在,求出所有满足条件的点P的坐标,若不存在,说明理由.2016—2017学年上海市建平中学高二(下)期中数学试卷参考答案与试题解析一.填空题1.设复数z=3+4i(i是虚数单位),则•z=25 .【考点】A5:复数代数形式的乘除运算.【分析】利用复数的运算法则即可得出.【解答】解:•z=(3+4i)•(3﹣4i)=32+42=25.故答案为:25.2.已知复数为纯虚数(i是虚数单位),则实数a= 4 .【考点】A5:复数代数形式的乘除运算.【分析】利用复数的运算法则、纯虚数的定义即可得出.【解答】解:复数==+i为纯虚数,∴=0,≠0,解得a=4.故答案为:4.3.已知点A、B到平面α的距离分别是4、6,则线段AB的中点M 到平面的距离α是5或1 .【考点】MK:点、线、面间的距离计算.【分析】由于A,B的位置可在同侧与异侧,故需要讨论.考虑两种情况:当A、B两点有平面α的同侧时,当A、B两点有平面α的异侧时,分别利用平面几何的知识求得M到平面α的距离即可.【解答】解:考虑两种情况:当A、B两点有平面α的同侧时,如图,分别过A、B、M作α的垂线,可得直角梯形,则AB中点M到平面α的距离为5;当A、B两点有平面α的异侧时,如图,分别过A、B、M作α的垂线,则,∴,则点M到平面α的距离为1.综上,点M到平面α的距离为5或1.故答案为:5或1.4.如图,正方体ABCD﹣A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于.【考点】LT:直线与平面平行的性质.【分析】根据已知EF∥平面AB1C和线面平行的性质定理,证明EF∥AC,又点E为AD的中点,点F在CD上,以及三角形中位线定理可知点F是CD的中点,从而求得线段EF的长度.【解答】解:∵EF∥平面AB1C,EF⊆平面AC,平面AB1C∩平面AC=AC,∴EF∥AC,又点E为AD的中点,点F在CD上,∴点F是CD的中点,∴EF=.故答案为.5.二面角α﹣l﹣β为60°,异面直线a、b分别垂直于α、β,则a 与b所成角的大小是60°.【考点】LM:异面直线及其所成的角.【分析】根据二面角的定义,及线面垂直的性质,我们可得若两条直线a,b分别垂直于两个平面,则两条直线的夹角与二面角相等或互补,由于已知的二面角α﹣l﹣β的平面角为60°,故异面直线所成角与二面角相等,即可得到答案.【解答】解:根据二面角的定义则线面垂直的性质,∵二面角α﹣l﹣β的平面角为60°,有两条异面直线a,b分别垂直于平面,设异面直线a,b的夹角为θ则θ=60°.故答案为:60°.6.已知A是△BCD所在平面外一点,E、F分别是BC和AD的中点,若BD⊥AC,BD=AC,则EF与BD所成角的大小是45°.【考点】LM:异面直线及其所成的角.【分析】取CD的中点G,利用三角形中位线的性质找出异面直线成的角∠FEG,把此角放在一个三角形中,解此三角形,求出此角的大小.【解答】解:取CD的中点G,连接EG、FG,则EG∥BD,所以相交直线EF与EG所成的锐角或直角即为异面直线EF与BD 所成的角.在Rt△EGF中,求得∠FEG=45°,即异面直线EF与BD所成的角为45°.7.双曲线3y2﹣x2=1的两条渐近线的夹角是.【考点】KC:双曲线的简单性质.【分析】根据题意,由双曲线的方程计算可得其渐近线方程,由渐近线方程得到渐近线的倾斜角,即可得到结论【解答】解:根据题意,双曲线的方程为:3y2﹣x2=1,其渐近线方程为y=±x,直线y=x的倾斜角为,直线y=﹣x的倾斜角为,则直线y=x与y=﹣x的夹角为,故答案为:.8.已知椭圆C:,点M与C的焦点不重合,若M关于C的焦点的对称点分别为A,B,线段MN的中点在C上,则|AN|+|BN|= 20 .【考点】K4:椭圆的简单性质.【分析】由题意作出图象,设线段MN的中点为D,连结DF1,DF2,用椭圆的定义解答即可.【解答】解:如图,设线段MN的中点为D,连结DF1,DF2,则DF1,DF2,分别是△AMN,△BMN的中位线,则|AN|+|BN|=2|DF1|+2|DF2|=2(|DF1|+|DF2|)=2×2a=4×5=20.故答案为:209.已知复数z满足|z+2﹣i|=1,则|2z﹣1|的取值范围是.【考点】A4:复数的代数表示法及其几何意义.【分析】复数z满足|z+2﹣i|=1,表示以C(﹣2,1)为圆心,1为半径的圆.可得|2z﹣1|=2|z﹣|表示圆上的点到P的距离的2倍.圆心C到点P的距离d.即可得出.【解答】解:复数z满足|z+2﹣i|=1,表示以C(﹣2,1)为圆心,1为半径的圆.则|2z﹣1|=2|z﹣|表示圆上的点到P的距离的2倍.圆心C到点P的距离d==.∴|2z﹣1|的取值最值分别为:2=±2.∴取值范围是:.故答案为:.10.设实系数一元二次ax2+bx+c=0的两根是x1、x2,下列命题中,假命题的序号是(1)(2)(1)方程可能有两个相等的虚根(2)ax2+bx+c=(x﹣x1)(x﹣x2)(3)(4)若b2﹣4ac<0,则x1﹣x2一定是纯虚数.【考点】A7:复数代数形式的混合运算.【分析】(1)实系数一元二次ax2+bx+c=0的两根是x1、x2,方程可能有两个共轭虚根,即可判断出真假.(2)由ax2+bx+c=a(x﹣x1)(x﹣x2),即可判断出真假.(3)x1+x2=﹣,x1x2=,可得+=(x1+x2)•x1x2,即可得出.(4)由b2﹣4ac<0,则x1﹣x2一定是纯虚数.即可得出.【解答】解:(1)实系数一元二次ax2+bx+c=0的两根是x1、x2,方程可能有两个共轭虚根,因此是假命题.(2)由于ax2+bx+c=a(x﹣x1)(x﹣x2),因此(2)是假命题.(3)∵x1+x2=﹣,x1x2=,∴+=(x1+x2)•x1x2=﹣•=,是真命题.(4)若b2﹣4ac<0,则x1﹣x2一定是纯虚数.因此是真命题.综上可得:假命题的序号是(1)(2).故答案为:(1)(2).11.定长是3的线段AB的两端点在抛物线y2=x上移动,M是线段AB的中点,则M到y轴距离的最小值是.【考点】K8:抛物线的简单性质.【分析】先设出A,B的坐标,根据抛物线方程可求得其准线方程,进而可表示出M到y轴距离,根据抛物线的定义,以及利用两边之和大于第三边且A,B,F三点共线时取等号判断出﹣≥﹣=﹣=,进而求得其最小值.【解答】解:设A(x1,y1) B(x2,y2),焦点为F(,0)抛物线准线x=﹣所求的距离为S=||=﹣=﹣,[两边之和大于第三边且A,B,F三点共线时取等号]∴﹣≥﹣=﹣=,故答案为:.12.斜率是1的直线与椭圆交于A、B两点,P为线段AB上的点,且AP=2PB,则点P的轨迹方程是148x2+13y2+64xy﹣20=0(在椭圆内).【考点】K4:椭圆的简单性质.【分析】设直线l的方程,代入椭圆方程,由x1,x2是方的两个根,分别求得x1,x2,由AP=2PB,求得x′=,代入即可即可求得P 的轨迹方程.【解答】解:设动点为P(x′,y′),则过y=x+(y′﹣x′),整理得:5x2+2(y′﹣x′)x+(y′﹣x′)2﹣4=0,(※)若直线l椭圆交于A(x1,y1),B(x2,y2),x1<x2,则x1,x2是方程(※)的两个根,且x1=,①x2=,②由AP=2PB,x1<x2,则x′=,代入整理得:4x′+y′=,丨y′﹣x′丨<,两边同时平方:148x′2+13y′2+64x′y′﹣20=0,∴点P的轨迹方程148x2+13y2+64xy﹣20=0(在椭圆内).故答案为:148x2+13y2+64xy﹣20=0(在椭圆内).二。
上海中考自招建平数学资料
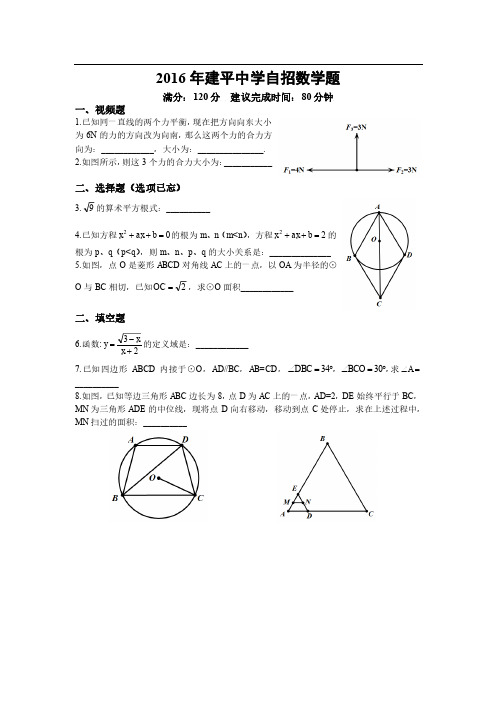
2016年建平中学自招数学题满分:120分 建议完成时间:80分钟一、视频题1.已知同一直线的两个力平衡,现在把方向向东大小为6N 的力的方向改为向南,那么这两个力的合力方向为:____________,大小为:_______________.2.如图所示,则这3个力的合力大小为:___________二、选择题(选项已忘)3.9的算术平方根式:__________4.已知方程02=++b ax x 的根为m 、n (m<n ),方程22=++b ax x 的根为p 、q (p<q ),则m 、n 、p 、q 的大小关系是:______________5.如图,点O 是菱形ABCD 对角线AC 上的一点,以OA 为半径的⊙O 与BC 相切,已知2=OC ,求⊙O 面积____________二、填空题6.函数:23+-=x x y 的定义域是:____________ 7.已知四边形ABCD 内接于⊙O ,AD//BC ,AB=CD ,,,︒=∠︒=∠3034BCO DBC 求=∠A __________8.如图,已知等边三角形ABC 边长为8,点D 为AC 上的一点,AD =2,DE 始终平行于BC ,MN 为三角形ADE 的中位线,现将点D 向右移动,移动到点C 处停止,求在上述过程中,MN 扫过的面积:__________三、解答题9.已知)(),(0,86,0B A ,点O 为AB 上的一点,以点O 为圆心,AO 为半径作圆,交AB 于点P ,AP=a .过点P 作x 轴的垂线段,垂足为点M.(1)求AB 的长;(2)如果⊙O 与x 轴相切,求a 的值,(3)点D 为x 轴上的一点,如果△AOD 与△DMP相似,请直接写出点D 的个数,及在该个数的情况下a 的取值范围.10.一名老师带领7名学生去参加数学竞赛,他们决定租车前往,每辆车可以乘坐4个人,于是他们决定分成A 、B 两组前往。
上海建平中学数学三角形解答题(提升篇)(Word版 含解析)

上海建平中学数学三角形解答题(提升篇)(Word 版 含解析)一、八年级数学三角形解答题压轴题(难)1.(1)如图1.在△ABC 中,∠B =60°,∠DAC 和∠ACE 的角平分线交于点O ,则∠O = °,(2)如图2,若∠B =α,其他条件与(1)相同,请用含α的代数式表示∠O 的大小; (3)如图3,若∠B =α,11,PAC DAC PCA E n nAC ∠=∠∠=∠,则∠P = (用含α的代数式表示).【答案】(1)∠O =60°;(2)90°-12α;(3)11(1)180P n nα∠=-⨯- 【解析】 【分析】(1)由题意利用角平分线的性质和三角形内角和为180°进行分析求解;(2)根据题意设∠BAC=β,∠ACB=γ,则α+β+γ=180°,利用角平分线性质和外角定义找等量关系,用含α的代数式表示∠O 的大小;(3)利用(2)的条件可知n=2时,∠P=111-18022α︒⨯-(),再将2替换成n 即可分析求解. 【详解】解:(1)因为∠DAC 和∠ACE 的角平分线交于点O ,且∠B=60°, 所以18060120OAC OCA οοο∠+∠=-=, 有∠O=180120οο-=60°.(2)设∠BAC=β,∠ACB=γ,则α+β+γ=180° ∵∠ACE 是△ABC 的外角, ∴∠ACE=∠B+∠BAC=α+β ∵CO 平分∠ACE11()22ACO ACE αβ∴∠=∠=+ 同理可得:1()2CAO αγ∠=+ ∵∠O+∠ACO+∠CAO=180°,∴11180180()()22O ACO CAO αβαγ︒︒∠=-∠-∠=-+-+1180()2αβαγ︒=-+++111180()1809090222αβααα︒︒︒︒=-++=--=-;(3)∵∠B=α,11,PAC DAC PCA E n nAC ∠=∠∠=∠, 由(2)可知n=2时,有∠P=1180902α︒︒--=111-18022α︒⨯-(),将2替换成n 即可, ∴11(1)180P n nα∠=-⨯-. 【点睛】本题考查用代数式表示角,熟练掌握并综合利用角平分线定义和三角形内角和为180°以及等量替换技巧与数形结合思维分析是解题的关键.2.如图, A 为x 轴负半轴上一点, B 为x 轴正半轴上一点, C(0,-2),D(-3,-2). (1)求△BCD 的面积;(2)若AC ⊥BC,作∠CBA 的平分线交CO 于P ,交CA 于Q,判断∠CPQ 与∠CQP 的大小关系, 并证明你的结论.【答案】(1)3;(2)∠CPQ =∠CQP ,理由见解析; 【解析】 【分析】(1)求出CD 的长度,再根据三角形的面积公式列式计算即可得解;(2)根据角平分线的定义可得∠ABQ=∠CBQ ,然后根据等角的余角相等解答; 【详解】解:(1)∵点C (0,-2),D (-3,-2), ∴CD=3,且CD//x 轴∴△BCD 面积=12×3×2=3; (2)∠CPQ =∠CQP , ∵AC ⊥BC ,∴∠ACO+∠BCO=90°,又∠ACO+∠OAC=90°∴∠OAC=∠BCO,又BQ平分∠CBA,∴∠ABQ=∠CBQ,∵∠CQP=∠OAC+∠ABQ∠CPQ=∠CBQ+∠BCO,∴∠CQP=∠CPQ(2)∠CPQ=∠CQP,∵AC⊥BC,∴∠ACO+∠BCO=90°,又∠ACO+∠OAC=90°∴∠OAC=∠BCO,又BQ平分∠CBA,∴∠ABQ=∠CBQ,∵∠CQP=∠OAC+∠ABQ∠CPQ=∠CBQ+∠BCO,∴∠CQP=∠CPQ【点睛】本题考查了坐标与图形性质,三角形的角平分线,三角形的面积,三角形的内角和定理,三角形的外角性质,综合题,熟记性质并准确识图是解题的关键.3.如图四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G.(1)求证:∠BAG=∠BGA;(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°.①若点E在线段AD上,求∠AFC的度数;②若点E在DA的延长线上,直接写出∠AFC的度数;(3)如图3,点P在线段AG上,∠ABP=2∠PBG,CH∥AG,在直线AG上取一点M,使∠PBM=∠DCH,请直接写出∠ABM:∠PBM的值.【答案】(1)证明见解析;(2)①20°;②160°;(3)13或73【解析】【分析】(1)根据AD//BC可知∠GAD=∠BGA,由AG平分∠BAD可知∠BAG=∠GAD,即可得答案.(2)①根据CF平分∠BCD,∠BCD=90°,可求出∠GCF的度数,由AD//BC可求出∠AEF 和∠DAB的度数,根据三角形外角的性质求出∠AFC的度数即可;②根据三角形外角性质求出即可;(3)根据M点在BP的上面和下面两种情况讨论,分别求出∠PBM和∠ABM 的值即可.【详解】(1)∵AD∥BC,∴∠GAD=∠BGA,∵AG平分∠BAD,∴∠BAG=∠GAD,∴∠BAG=∠BGA;(2)①∵CF平分∠BCD,∠BCD=90°,∴∠GCF=45°,∵AD∥BC,∠ABC=50°,∴∠AEF=∠GCF=45°;∠DAB=180°﹣50°=130°,∵AG平分∠BAD,∴∠BAG=∠GAD=65°,∴∠AFC=65°﹣45°=20°;②如图:∵∠AGB=65°,∠BCF=45°,∴∠AFC=∠CGF+∠BCF=115°+45°=160°;(3)有两种情况:①当M在BC的下方时,如图:∵∠ABC=50°,∠ABP=2∠PBG,∴∠ABP=(1003)°,∠PBG=(503)°,∵AG∥CH,∴∠BCH=∠AGB=65°,∵∠BCD=90°,∴∠DCH=∠PBM=90°﹣65°=25°,∴∠ABM=∠ABP+∠PBM=(1003+25)°=(1753)°,∴∠ABM:∠PBM=(1753)°:25°=73;②当M在BC的上方时,如图:同理得:∠ABM=∠ABP﹣∠PBM=(1003﹣25)°=(253)°,∴∠ABM:∠PBM=(253)°:25°=13;综上,∠ABM:∠PBM的值是13或73.【点睛】本题考查平行线的性质和三角形外角性质,熟练掌握平行线性质是解题关键.4.已知:如图①,BP、CP分别平分△ABC的外角∠CBD、∠BCE,BQ、CQ分别平分∠PBC、∠PCB,BM、CN分别是∠PBD、∠PCE的角平分线.(1)当∠BAC=40°时,∠BPC=,∠BQC=;(2)当BM∥CN时,求∠BAC的度数;(3)如图②,当∠BAC=120°时,BM、CN所在直线交于点O,直接写出∠BOC的度数.【答案】(1) 70°,125°;(2)∠BAC=60° (3) 45°【解析】分析:(1)根据三角形的外角性质分别表示出∠DBC与∠BCE,再根据角平分线的性质可求得∠CBP+∠BCP,最后根据三角形内角和定理即可求解;根据角平分线的定义得出∠QBC=12∠PBC ,∠QCB=12∠PCB,求出∠QBC+∠QCB 的度数,根据三角形内角和定理求出即可;(2)根据平行线的性质得到∠MBC+∠NCB=180°,依此求解即可;(3)根据题意得到∠MBC+∠NCB,再根据三角形外角的性质和三角形内角和定理得到∠BOC 的度数.详解:(1)∵∠DBC=∠A+∠ACB ,∠BCE=∠A+∠ABC , ∴∠DBC+∠BCE=180°+∠A=220°,∵BP 、CP 分别是△ABC 的外角∠CBD 、∠BCE 的角平分线,∴∠CBP+∠BCP=12(∠DBC+∠BCE )=110°, ∴∠BPC=180°﹣110°=70°,∵BQ 、CQ 分别是∠PBC 、∠PCB 的角平分线,∴∠QBC=12∠PBC ,∠QCB=12∠PCB , ∴∠QBC+∠QCB=55°, ∴∠BQC=180°﹣55°=125°; (2)∵BM ∥CN ,∴∠MBC+∠NCB=180°,∵BM 、CN 分别是∠PBD 、∠PCE 的角平分线,∴34(∠DBC+∠BCE )=180°, 即34(180°+∠BAC )=180°, 解得∠BAC=60°; (3)∵∠BAC=120°,∴∠MBC+∠NCB=34(∠DBC+∠BCE )=34(180°+α)=225°,∴∠BOC=225°﹣180°=45°.点睛:本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.5.ABC 中,AD 是BAC ∠的平分线,AE BC ⊥,垂足为E ,作CF//AD ,交直线AE 于点F.设B α∠=,ACB β∠=.()1若B 30∠=,ACB 70∠=,依题意补全图1,并直接写出AFC ∠的度数; ()2如图2,若ACB ∠是钝角,求AFC ∠的度数(用含α,β的式子表示);()3如图3,若B ACB ∠∠>,直接写出AFC ∠的度数(用含α,β的式子表示).【答案】(1)补图见解析,AFC 20∠=;(2) ()1AFC 180βα2∠=--;(3) ()1AFC αβ2∠=-. 【解析】 【分析】(1)先根据三角形内角和定理求出∠BAC 和∠CAE ,根据角平分线定义求出∠CAD ,即可求出答案;(2)先根据三角形内角和定理求出∠BAC ,根据角平分线定义求出∠BAD ,根据三角形外角性质求出∠ADC ,根据三角形内角和定理求出∠DAE ,根据平行线的性质求出即可; (3)求出∠DAE 度数,根据平行线的性质求出即可. 【详解】 解:()1如图1,B 30∠=,ACB 70∠=,BAC 180B ACB 80∠∠∠∴=--=,AD 是BAC ∠的平分线,1CAD CAB 402∠∠∴==,AE BC ⊥,AEC 90∠∴=,ACB 70∠=,EAC 180907020∠∴=--=,DAE CAD CAE 402020∠∠∠∴=-=-=,CF//AD ,AFC DAE 20∠∠∴==;()2如图2,ABC 中,BAC B ACB 180∠∠∠++=, ()BAC 180B ACB ∠∠∠∴=-+. ()180αβ=-+,AD 是BAC ∠的平分线,()11BAD BAC 90αβ22∠∠∴==-+,()()11ADE B BAD α90αβ90βα22∠∠∠∴=+=+-+=--,AE BC ⊥,DAE ADE 90∠∠∴+=,()1DAE 90ADE βα2∠∠∴=-=-, CF//AD ,DAE AFC 180∠∠∴+=,()1AFC 180βα2∠∴=--; ()3如图3,ABC 中,BAC B ACB 180∠∠∠++=, ()BAC 180B ACB ∠∠∠∴=-+, ()180αβ=-+,AD 是BAC ∠的平分线,()11CAD BAC 90αβ22∠∠∴==-+,AE BC ⊥,AEC 90∠∴=, ACB β∠=,EAC 18090β90β∠∴=--=-,()()()11DAE CAE CAD 90β90αβαβ22∠∠∠⎡⎤∴=-=----=-⎢⎥⎣⎦.【点睛】本题考查了三角形内角和定理、三角形角平分线定义、三角形的高、平行线的性质等,熟练掌握相关的性质与定理是解题的关键.6.我校快乐走班数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°)小棒依次摆放在两射线之间,并使小棒两端分别落在两射线上.活动一:如图甲所示,从点A 1开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A 1A 2为第1根小棒.数学思考:(1)小棒能无限摆下去吗?答: .(填“能“或“不能”) (2)设AA 1=A 1A 2=A 2A 3=1.则θ= 度;活动二:如图乙所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.数学思考:(3)若只能摆放5根小棒,求θ的范围.【答案】(1)能.(2)θ=22.5;(3) 15°≤θ<18°.【解析】【分析】(1)根据已知条件:小棒两端能分别落在两射线上进行判断即可;(2)根据等腰三角形的性质和三角形的外角性质即得结果;(3)根据等腰三角形的性质和三角形的内角和定理可得关于θ的不等式组,解不等式组即得结果.【详解】(1)∵根据已知条件∠BAC=θ(0°<θ<90°)小棒两端能分别落在两射线上,∴小棒能继续摆下去;(2)∵A1A2=A2A3,A1A2⊥A2A3,∴∠A2A1A3=45°,∴∠AA2A1+∠θ=45°,∵∠AA2A1=∠θ,∴∠θ=22.5°;(3)如图乙,∵A2A1=A2A3,∴∠A2A3A1=∠A2A1A3=2θ°,∵A2A3=A4A3,∴∠A3A2A4=∠A3A2A4=3θ°,∵A4A3=A4A5,∴∠A4A3A5=∠A4A5A3=4θ°,根据三角形内角和定理和等腰三角形的性质,可得6θ⩾90°,5θ<90°,∴15°⩽θ<18°.【点睛】本题考查了等腰三角形的性质、三角形内角和定理和三角形的外角性质,根据题意找出规律并结合等腰三角形的性质是解题的关键.7.已知△ABC,(1)如图1,若D点是△ABC内任一点、求证:∠D=∠A+∠ABD+∠ACD.(2)若D点是△ABC外一点,位置如图2所示.猜想∠D、∠A、∠ABD、∠ACD有怎样的关系?请直接写出所满足的关系式.(不需要证明)(3)若D点是△ABC外一点,位置如图3所示、猜想∠D、∠A、∠ABD、∠ACD之间有怎样的关系,并证明你的结论.【答案】(1)证明见解析;(2)∠D+∠A+∠ABD+∠ACD=360°;(3)∠D+∠ACD=∠A+∠ABD,证明见解析.【解析】试题分析:(1)由∠BDC=∠2+∠CED,∠CED=∠A+∠1,可以得出∠D=∠A+∠ABD+∠ACD.(2)由∠D+∠A+∠ABD+∠ACD=∠A+∠ABC+∠ACB+∠D+∠DBC+DCB,∠A+∠ABC+∠ACB=180°,∠D+∠DBC+DCB=180°,可以得出∠D+∠A+∠ABD+∠ACD=360°.(3)根据三角形的外角性质定理即三角形的一个外角等于与它不相邻的两个内角之和,可知∠AED=∠1+∠A,∠AED=∠D+∠2,所以可知∠A+∠1=∠D+∠2即∠D+∠ACD=∠A+∠ABD. 试题解析:(1)证明:延长BD 交AC 于点E .∵∠BDC 是△CDE 的外角,∴∠BDC=∠2+∠CED,∵∠CED 是△ABE 的外角,∴∠CED=∠A+∠1.∴∠BDC=∠A+∠1+∠2.即∠D=∠A+∠ABD+∠ACD.(2)∵∠D+∠A+∠ABD+∠ACD=∠A+∠ABC+∠ACB+∠D+∠DBC+DCB,∠A+∠ABC+∠ACB=180°,∠D+∠DBC+∠DCB=180°,∴∠D+∠A+∠ABD+∠ACD=360°.(3)证明:令BD 、AC 交于点E ,∵∠AED 是△ABE 的外角,∴∠AED=∠1+∠A,∵∠AED 是△CDE 的外角,∴∠AED=∠D+∠2.∴∠A+∠1=∠D+∠2即∠D+∠ACD=∠A+∠ABD.点睛:本题主要考查三角形的外角性质及三角形的内角和定理,解题的关键是熟练掌握三角形的外角性质定理即三角形的一个外角等于与它不相邻的两个内角之和.8.已知,在ABC 中,∠A =60°,(1)如图①,∠ABC 和∠ACB 的角平分线交于点O ,则∠BOC= ;(2)如图②,∠ABC 和∠ACB 的三等分线分别对应交于点O 1,O 2,则2_________BO C ∠=;(3)如图③,∠ABC 和∠ACB 的n 等分线分别对应交于点O 1,O 2,……,1n O -(内部有1n -个点),则1-∠=n BO C ;(4)如图③,∠ABC 和∠ACB 的n 等分线分别对应交于点O 1,O 2,……,1n O -,若190-∠=︒n BO C ,求n 的值.【答案】(1)120°;(2)100°;(3)60120+⎛⎫︒⎪⎝⎭n n ;(4)n=4 【解析】【分析】 (1)根据三角形的内角和定理即可求出∠ABC +∠ABC ,然后根据角平分线的定义即可求出∠OBC +∠OCB ,再根据三角形的内角和定理即可求出结论;(2)根据三角形的内角和定理即可求出∠ABC +∠ABC ,然后根据三等分线的定义即可求出∠O 2BC +∠O 2CB ,再根据三角形的内角和定理即可求出结论; (3)根据三角形的内角和定理即可求出∠ABC +∠ABC ,然后根据n 等分线的定义即可求出∠O n -1BC +∠O n -1CB ,再根据三角形的内角和定理即可求出结论; (4)根据(3)的结论列出方程即可求出结论.【详解】解:(1)∵在ABC 中,∠A =60°,∴∠ABC +∠ABC=180°-∠A=120°∵∠ABC 和∠ACB 的角平分线交于点O ,∴∠OBC=12∠ABC ,∠OCB=12∠ACB ∴∠OBC +∠OCB=12∠ABC +12∠ACB =12(∠ABC +∠ACB ) =60°∴∠BOC=180°-(∠OBC +∠OCB )=120°故答案为:120°.(2)∵在ABC 中,∠A =60°,∴∠ABC +∠ABC=180°-∠A=120°∵∠ABC 和∠ACB 的三等分线分别对应交于点O 1,O 2,∴∠O 2BC=23∠ABC ,∠O 2CB=23∠ACB ∴∠O 2BC +∠O 2CB=23∠ABC +23∠ACB=23(∠ABC +∠ACB ) =80° ∴2∠=BO C 180°-(∠O 2BC +∠O 2CB )=100°故答案为:100°.(3)∵在ABC 中,∠A =60°,∴∠ABC +∠ABC=180°-∠A=120°∵∠ABC 和∠ACB 的n 等分线分别对应交于点O 1,O 2,……,1n O -∴∠O n -1BC=1n n -∠ABC ,∠O n -1CB=1n n-∠ACB ∴∠O n -1BC +∠O n -1CB=1n n -∠ABC +1n n -∠ACB =1n n-(∠ABC +∠ACB ) =120120-⎛⎫ ⎪⎝⎭n n ° ∴1-∠=n BO C 180°-(∠O 2BC +∠O 2CB )=60120+⎛⎫︒⎪⎝⎭n n 故答案为:60120+⎛⎫︒ ⎪⎝⎭n n (4)由(3)知:1-∠=n BO C 60120+⎛⎫︒ ⎪⎝⎭n n ∴6012090+=n n解得:n=4 经检验:n=4是原方程的解.【点睛】本题考查了n 等分线的定义和三角形的内角和定理,掌握n 等分线的定义和三角形的内角和定理是解决此题的关键.9.已知:△ABC 中 ∠A=64°, 角平分线BP 、CP 相交于点P .1若BP 、CP 是两内角的平分线,则∠BPC=_____(直接填数值) 求证:01902BPC A ∠=+∠. 2若BP 、CP 是两外角的平分线,则∠BPC=_____(直接填数值)3若BP 、CP 是一内角的平分线,一外角的平分线,则∠BPC=_______(直接填数值)4 由①②③的数值计算可知:∠BPC 与∠A 有着密切的数量关系,请就第②③写出你的发现【答案】(1)122°;(2)58°;(3)32°.(4).若BP 、CP 是两外角的平分线,则∠BPC=90°-12∠A ; 若BP 、CP 是一内角的平分线,一外角的平分线,则∠BPC=12∠A . 【解析】【分析】①根据三角形角平分线的性质可得,∠BPC +∠PCB =90°-12∠A ,根据三角形内角和定理可得∠BPC =90°+12∠A ; ②根据三角形外角平分线的性质可得∠BCP =12(∠A +∠ABC )、∠PBC =12(∠A +∠ACB );根据三角形内角和定理可得∠BPC =90°-12∠A ; ③根据BP 为∠ABC 的角平分线,CP 为△ABC 外角∠ACE 的平分线,可知,∠A =180°-∠1-∠3,∠P =180°-∠4=∠5=180°-∠3-12(∠A +2∠1),两式联立可得2∠P =∠A . ④根据前面的情况直接写出∠BPC 与∠A 的数量关系,【详解】 解:(1)证明:∵在△ABC 中,PB 、PC 分别是∠ABC 、∠ACB 的平分线,∠A 为x ° ∴∠PBC +∠PCB =12(180°-∠A )=12×(180°-x °)=90°-12∠A故∠BPC=180°-(∠PBC+∠PCB)=180°-(90°-12∠A)=90°+12∠A;则∠BPC=122°;(2)理由如下:∵BP、CP为△ABC两外角∠ABC、∠ACB的平分线,∠A为x°∴∠BCP=12(∠A+∠ABC)、∠PBC=12(∠A+∠ACB),由三角形内角和定理得,∠BPC=180°-∠BCP-∠PBC,=180°-12[∠A+(∠A+∠ABC+∠ACB)],=180°-12(∠A+180°),=90°-12∠A;则∠BPC=58°;(3)如图:∵BP为∠ABC的内角平分线,CP为△ABC外角∠ACE的平分线,两角平分线交于点P,∴∠1=∠2,∠5=12(∠A+2∠1),∠3=∠4,在△ABE中,∠A=180°-∠1-∠3∴∠1+∠3=180°-∠A----①在△CPE中,∠P=180°-∠4-∠5=180°-∠3-12(∠A+2∠1),即2∠P=360°-2∠3-∠A-2∠1=360°-2(∠1+∠3)-∠A----②,把①代入②得2∠P=∠A.则∠BPC=32°;(4)若BP、CP是两外角的平分线,则∠BPC=90°-12∠A;若BP、CP是一内角的平分线,一外角的平分线,则∠BPC=12∠A.故填为:(1)122°;(2)58°;(3)32°.【点睛】此类题目考查的是三角形内角与外角的关系,角平分线的性质,三角形内角和定理,属中学阶段的常规题.10.已知:如图,等边三角形ABD与等边三角形ACE具有公共顶点A,连接CD,BE,交于点P.(1)观察度量,BPC∠的度数为____.(直接写出结果)(2)若绕点A将△ACE旋转,使得180BAC∠=︒,请你画出变化后的图形.(示意图)(3)在(2)的条件下,求出BPC∠的度数.【答案】(1)120°;(2)作图见解析;(3)∠BPC =120°.【解析】分析:(1)∠BPC的度数为120°,理由为:由△ABD与△ACE都是等边三角形,利用等边三角形的性质得到∠DAB=∠ABD=∠CAE=60°,AD=AB,AC=AE,利用等式的性质得到夹角相等,利用SAS得出三角形DAC与三角形BAE全等,由全等三角形的对应角相等得到∠ADC=∠ABE,利用外角性质,等量代换即可得到所求;(2)作出相应的图形,如图所示;(3)解法同(1),求出∠BPC的度数即可.本题解析:(1)∠BPC的度数为120°,理由为:证明:∵△ABD与△ACE都是等边三角形,∴∠DAB=∠ABD=∠CAE=60°,AD=AB,AC=AE,∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,在△DAC与△BAE中,{AD ABDAC BAEAC AE=∠=∠=,∴△DAC≌△BAE(SAS),∴∠ADC=∠ABE,∵∠ADC+∠CDB=60°,∴∠ABE+∠CDB=60°,∴∠BPC=∠DBP+∠PDB=∠ABE+∠CDB+∠ABC=120°;(2)作出相应的图形,如图所示;(3)∵△ABD与△ACE都是等边三角形,∴∠ADB=∠BAD=∠ABD=∠CAE=60°,AD=AB,AC=AE,∴∠DAB+∠DAE=∠CAE+∠DAE,即∠DAC=∠BAE,在△DAC与△BAE中,{AD ABDAC BAC AC AE=∠=∠=,∴△DAC≌△BAE(SAS),∴∠ADC=∠ABE,∵∠ABE+∠DBP=60°,∴∠ADC+∠DBP=60°,∴∠BPC=∠BDP+∠PBD=∠ADC+∠DBP+∠ADB=120°.点睛:本题考查了等边三角形的性质,外角性质,以及全等三角形的判定与性质,熟练掌握等边三角形的性质是解本题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4、已知方程 x2 ax b 0 的根为 m , n m n ,方程 x2 ax b 2 的根为 p , q p q ,则 m , n , p , q 的
大小关系是____________________. 【解析】 p m n q 5、如图,点 O 是菱形 ABCD 对角线 AC上 的一点,以 OA 为半径的 O 与 BC 相切,已知 OC 2 ,则 O 面积是 ________________________.
四、解答题 9、已知 A(0,6) , B(8,0) ,点 O 为 AB 上的一点,以点 O 为圆心, AO 为半径作圆,交 AB 于点 P , AP a ,过点 P 作 x 轴的垂线段,垂足为点 M . (1)求 AB 的长; (2)如果 O 与 x 轴相切,求 a 的值, (3)点 D 为 x 轴上的一点,如果 AOD 与 DMP 相似,请直接写出点 D 的个数及在该个数的情况下 a 的取值范围. 【解析】(1) AB 10 (2) a 15
【解析】(1) tn a n 1d
(2)
Sn
na
nn 1
d 2
3 尹充
【解析】(1) y 2x2 8x 6
(2) 9 2
(3) (1,0)
12、(英语题,翻译出来大致如下)高斯用下述方法求出了 S 1 2 3 99 100 的值: S 1 2 3 99 10( S 100 99 98 2 1
Hale Waihona Puke 乘坐的车.已知人行走的速度为 5km / h ,车速为 60km / h ,从故障发生起 42 分钟后不得进入考场.
(1)师生们决定让车先送 B 组去考场, A 组在原地等候,等车辆返回后再送 A 组去考场,请通过计算说明: A 组能
否进入考场?
(2)为了节省时间,队伍中的小红同学建议先让车送 B 组去考场, A 组向前行走,等车辆返回时沿路遇上 A 组后再送
8、如图,已知等边 ABC 边长为 8 ,点 D 为 AC 上的一点, AD 2 , DE E 始终平行于 BC , MN 为 ADE 的中位 线,现将点 D 向右移动,移动到点 C 处停止,则在上述过程中, MN 扫过的面积是__________________. 【解析】 15 3
4
1 尹充
他们去考场,绘制出的函数图象如图 1 所示(时间利路程均从出故障后算起):
①求直线 OA 的函数解析式;
②求 a 的值;
(3)老师进一步改进了方案:先让车送 B 组去考场, A 组向前行走,车辆行驶到离考场还有一段距离时方 B 组同学下
车,然后返回,沿路遇上 A 后送他们去考场,已知在这个方案下 A 、 B 两组同学同时到达考场,绘制函数图象如图
2 (3) a 60 ,有一个 D 点
11 0 a 5 且 a 60 时, D 不存在
11
10、一名老师带领 7 名学生去参加数学竞赛,他们决定租车前往,每辆车可以乘坐 4 个人,于是他们决定分成 A ,
B 两组前往,当两辆车行驶到离考场15km 处时,A 组乘坐的车出现故障无法行驶,唯一能使用的交通工具只有 B 组
2016 年建平中学自招数学题
满分:120 分 建议完成时间:80 分钟 一、视频题 1、已知同一直线的两个力平衡,现在把方向向东大小为 6N 的力的方向改为向南,那么这两个力的合力方向为:____, 大小为:_________________. 【解析】西南方向: 6 2N 2、如图所示,则这 3 个力的合力大小为:___________________. 【解析】 10N 二、选择题(选项已忘) 3、 9 的算术平方根式是_______________________.
2S 1 100 2 99 3 97 100 1 101 101 101
S 101100 5050 2
现有: Sn a a d a 2d tn d tn ,请用同样的方法用含 a 、 d 的代数式表示 tn 和 Sn ,
【解析】
2
三、填空题 6、函数: y 3 x 的定义域是__________________.
x2 【解析】 x 3 且 x 2 7、已知四边形 ABCD 内接于 O , AD / /BC , AB CD , DBC 34 , BCO 30 ,则 A __________. 【解析】 BAD 94
2 所示,请直接写出点 P 坐标.
【解析】(1) 15 15 15 3 h 42 min ,所以不能进入考场
60
4
(2) y 1 x , a 35
12
52
(3)
37 60
,
15
2 尹充
11、如图,己知抛物线 y 2x2 bx c 经过点 A(3,0) 和 B(1,0) ,交 y 轴与点 C ,点 P 从点 C 出发沿抛物线运动,到 点 A 时停止运动,过点 P 作 PD y 轴交 AC 于点 D . (1)求抛物线解析式; (2)求 PD 的最大值: (3)如果 APD 为直角三角形,求点 P 坐标.
