2012年中考数学试题分类汇编《三角形》及解析
【中考12年】浙江省温州市2001-2012年中考数学试题分类解析 专题9 三角形

2001-2012年某某某某中考数学试题分类解析汇编(12专题)专题9:三角形一、选择题1. (2001年某某某某3分)等腰三角形的一个底角是30°,则它的顶角是【】A.30° B.40° C.75° D.120°【答案】D。
【考点】等腰三角形的性质,三角形内角和定理。
【分析】根据等腰三角形底角相等的性质和三角形内角和定理,它的顶角是1800-2×300=1200。
故选D。
2. (2001年某某某某3分)在Rt△ABC中,∠C=90°,BC=4,AC=3,则tanA的值是【】A.43B.34C.35D.45【答案】A。
【考点】锐角三角函数定义。
【分析】根据正切函数定义,得tanA=BC4AC3=。
故选A。
3. (2002年某某某某4分)在△ABC中,点D、E分别在边AB,AC上,且DE∥BC,AE=3,EC=2,那么S△ADE:S△ABC等于【】A.2:3 B.3:5 C 9:4 D 9:25【答案】D。
【考点】相似三角形的判定和性质。
【分析】∵AE=3,EC=2,∴AE3 AC5=。
∵DE∥BC,∴△ADE∽△ABC。
∴22ADEABCS AE39S AC525∆∆⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭==。
故选D。
4. (2004年某某某某4分)如图,△ABC 中,∠C=90°,AB=5,BC=3,CA=4,那么sinA 等于【 】(A)43 (B) 34 (C) 53 (D)54 【答案】C 。
【考点】锐角三角函数定义, 【分析】根据正弦函数定义,得sinA=BC 3AB 5=。
故选C 。
5. (2006年某某某某4分)如图,在△ABC 中,∠C=90°,BC=5,AC=12,则 cosA 等于【 】A.512 B. 513 C. 125 D. 1213【答案】D 。
【考点】勾股定理,锐角三角函数定义。
【分析】∵在△ABC 中,∠C=90°,BC=5,AC=12,∴根据勾股定理得2222AB BC AC 51213=+=+=。
2012年全国中考数学试题分类解析汇编专题52:平面几何的综合
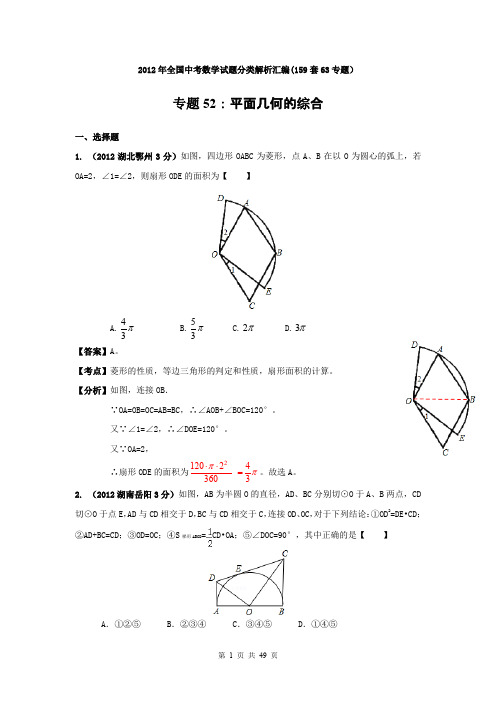
2012年全国中考数学试题分类解析汇编(159套63专题)专题52:平面几何的综合一、选择题1. (2012湖北鄂州3分)如图,四边形OABC 为菱形,点A 、B 在以O 为圆心的弧上,若OA=2,∠1=∠2,则扇形ODE 的面积为【 】A.π34B.π35C.π2D.π3【答案】A 。
【考点】菱形的性质,等边三角形的判定和性质,扇形面积的计算。
【分析】如图,连接OB .∵OA=OB=OC=AB=BC,∴∠AOB+∠BOC=120°。
又∵∠1=∠2,∴∠DOE=120°。
又∵OA=2,∴扇形ODE 的面积为21202 4 3603ππ⋅⋅=。
故选A 。
2. (2012湖南岳阳3分)如图,AB 为半圆O 的直径,AD 、BC 分别切⊙O 于A 、B 两点,CD 切⊙O 于点E ,AD 与CD 相交于D ,BC 与CD 相交于C ,连接OD 、OC ,对于下列结论:①OD 2=DE•CD; ②AD+BC=CD;③OD=OC;④S 梯形ABCD =CD•OA;⑤∠DOC=90°,其中正确的是【 】A .①②⑤ B.②③④ C.③④⑤ D.①④⑤【答案】A 。
【考点】切线的性质,切线长定理,相似三角形的判定与性质。
1052629【分析】如图,连接OE ,∵AD 与圆O 相切,DC 与圆O 相切,BC 与圆O 相切,∴∠DAO=∠DEO=∠OBC=90°,∴DA=DE,CE=CB ,AD∥BC。
∴CD=DE+EC=AD+BC。
结论②正确。
在Rt△ADO 和Rt△EDO 中,OD=OD ,DA=DE ,∴Rt△ADO≌Rt△EDO(HL )∴∠AOD=∠EOD。
同理Rt△CEO≌Rt△CBO,∴∠EOC=∠BOC。
又∠AOD+∠DOE+∠EOC+∠COB=180°,∴2(∠DOE+∠EOC)=180°,即∠DOC=90°。
结论⑤正确。
∴∠DOC=∠DEO=90°。
2012年全国中考数学试题分类解析汇编专题46:相似和位似

2012年全国中考数学试题分类解析汇编(159套63专题)专题46:相似和位似一、选择题1. (2012海南省3分)如图,点D 在△ABC 的边AC 上,要判断△ADB 与△ABC 相似,添加一个条件,不正确...的是【 】A .∠ABD=∠C B.∠ADB=∠ABC C.AB CB BD CD = D .AD AB AB AC= 【答案】C 。
【考点】相似三角形的判定。
【分析】由∠ABD=∠C 或∠ADB=∠ABC,加上∠A 是公共角,根据两组对应相等的两三角形相似的判定,可得△ADB∽△ABC;由AD AB AB AC=,加上∠A 是公共角,根据两组对应边的比相等,且相应的夹角相等的两三角形相似的判定,可得△ADB∽△ABC;但AB CB BD CD =,相应的夹角不知相等,故不能判定△ADB 与△ABC 相似。
故选C 。
2. (2012陕西省3分)如图,在△ABC 中,AD ,BE 是两条中线,则EDC ABC S S :∆∆=【 】A .1∶2B .2∶3C .1∶3D .1∶4【答案】D 。
【考点】三角形中位线定理,相似三角形的判定和性质。
【分析】∵△ABC 中,AD 、BE 是两条中线,∴DE 是△ABC 的中位线,∴DE∥AB,DE=12AB 。
∴△EDC∽△ABC。
∴()2EDC ABC S :S ED:AB =1:4∆∆=。
故选D 。
3. (2012浙江湖州3分)△ABC 中的三条中位线围成的三角形周长是15cm ,则△ABC 的周长为【 】A .60cmB .45cmC .30cmD .152cm 【答案】C 。
【考点】三角形中位线定理,相似三角形的性质。
【分析】∵三角形的中位线平行且等于底边的一半,∴△ABC 三条中位线围成的三角形与△ABC 相似,且相似比是12。
∵△ABC 中的三条中位线围成的三角形周长是15cm ,∴△ABC 的周长为30cm 。
故选C 。
4. (2012湖北咸宁3分)如图,正方形OABC 与正方形ODEF 是位似图形,O 为位似中心,相似比为1∶2,点A 的坐标为(1,0),则E 点的坐标为【 】.A .(2,0)B .(23,23)C .(2,2)D .(2,2)【答案】C 。
中考数学三角形试题归类(含答案)

中考数学三角形试题归类(含答案) 以下是查字典数学网为您推荐的中考数学三角形试题归类(含答案),希望本篇文章对您学习有所帮助。
中考数学三角形试题归类(含答案)选择题1. (天津3分)sin45的值等于(A) (B) (C) (D) 1【答案】B。
【考点】特殊角三角函数。
【分析】利用特殊角三角函数的定义,直接得出结果。
2.(河北省3分)如图,在△ABC 中,C=90,BC=6,D,E 分别在 AB、AC上,将△ABC沿DE折叠,使点A落在点A处,若A为CE的中点,则折痕DE的长为A、 B、2 C、3 D、4【答案】B。
【考点】翻折变换(折叠问题),相似三角形的判定和性质。
【分析】∵△ABC沿DE折叠,使点A落在点A处,EDA=EDA=90,AE=AE,△ACB∽△AED。
又∵A为CE的中点,AE=AE=AC。
ED=2。
故选B。
3.(山西省2分)如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为A. cmB.4cmC. cmD. cm【答案】D。
【考点】等腰三角形的性质,三角形中位线定理,正方形的性质,勾股定理。
【分析】根据三角形的中位线定理可得出BC=4,由AB=AC,可证明BG=CF=1,由勾股定理可求出CE= ,即可得出AC=2 。
故选D。
4.(内蒙古呼和浩特3分)如果等腰三角形两边长是6cm和3cm,那么它的周长是A、9cmB、12cmC、15cm或12cmD、15cm【答案】D。
【考点】等腰三角形的性质,三角形三边关系。
【分析】求等腰三角形的周长,即要确定等腰三角形的腰与底的长,根据三角形三边关系知当6为腰,3为底时,6﹣36+3,能构成等腰三角形,周长为6+6+3=15;当3为腰,6为底时,3+3=6,不能构成三角形。
故选D。
5.(内蒙古呼伦贝尔3分)如图,△ACB≌△A1CB1, BCB1=30,则ACA1的度数为A. 20B. 30C. 35D. 40【答案】B。
【中考12年】江苏省淮安市2001-2012年中考数学试题分类 专题9 三角形

【中考12年】江苏省淮安市2001-2012年中考数学试题分类 专题9三角形选择题1. (2002年江苏淮安3分)使两个直角三角形全等的条件是【 】A .一个锐角对应相等B .两个锐角对应相等C .一条边对应相等D .两条边对应相等2. (2002年江苏淮安3分)等边三角形的外接圆半径与它的内切圆半径之比是【 】A .1B 1:C .21 :D :23. (2002年江苏淮安3分)已知△ABC 的三边长分别是3cm 、4cm 、5cm ,则△ABC 的面积是【 】A .6cm2B .7.5cm 2C .10cm2D .12cm2【答案】A 。
【考点】勾股定理逆定理。
【分析】∵△ABC 的三边长分别是3cm 、4cm 、5cm ,且222345+=,∴△ABC 是直角三角形。
∴△ABC 的面积是13462⨯⨯=(cm2)。
故选A 。
5. (2004年江苏淮安3分)如图,小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度,已知她与树之间的距离为9.0 m,眼睛与地面的距离为1.6m,那么这棵树的高度大约是【】=+=≈⨯+=≈。
∵CE=BD=1.6m,∴AE AC CE 1.63 1.73 1.6 6.79 6.8∴这棵树的高度大约是6.8m。
故选B。
6. (2005年江苏淮安课标3分)如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A:25米,离路灯B:5米,如果小亮的身高为1.6米,那么路灯高度为【】7. (2005年江苏淮安课标3分)如图,点D 、E 、F 分别是△ABC (AB >AC )各边的中点,下列说法中,错误的是【 】AD 平分∠BAC B . EF=21BCC . EF 与AD 互相平分 D . △DFE 是△ABC 的位似图形【答案】A 。
【考点】反证法,三角形中位线定理,平行四边形的判定和性质,位似的判定。
江苏省泰州市2001-2012年中考数学试题分类解析 专题9 三角形

2001-2012年江苏泰州中考数学试题分类解析汇编(12专题)专题9:三角形一、选择题1.(江苏省泰州市2002年4分)Rt△ABC中,∠C=90°,a:b=3:4,运用计算器计算,∠A的度数是【】(精确到1°)A、30°B、37°C、38°D、39°【答案】B。
【考点】三角函数定义,计算器的应用。
【分析】根据题中所给的条件,在直角三角形中应用正切函数解题:∵Rt△ABC中,∠C=90°,,∴tan A= a:b=3:4=0.75。
运用计算器得,∠A≈37°。
故选B。
2.(江苏省泰州市2003年4分)如图,某防洪大坝的横断面是梯形,斜坡AB的坡度i=1∶2.5,则斜坡AB的坡角 为【】(精确到1°)A.24° B.22° C.68° D.66°【答案】B。
【考点】解直角三角形的应用(坡度坡角问题),正切函数定义,计算器的应用。
【分析】算出坡角的正切值,用计算器即可求得坡角:如图,∵坡度tanα=铅直高度AC:水平距离BC=1:2.5=0.4,∴α=21.8°≈22°。
故选B。
3.(江苏省泰州市2003年4分)在Rt△ABC的直角边AC边上有一点P(点P与点A、C不重合),过点P作直线截△ABC,使截得的三角形与△ABC相似,满足条件的直线共有【】A.1条 B.2条 C.3条 D.3条或4条【答案】D。
【考点】相似三角形的判定。
【分析】过点P作直线与另一边相交,使所得的三角形与原三角形已经有一个公共角,只要再作一个等于△ABC 的另一个角即可:(1)若AC <BC (如图1),过点P 作PD 1⊥AB,或作PD 2⊥AC,或作PD 3∥AB,或作∠PD 4C=∠A,这样截得的三角形与△ABC 相似。
即满足条件的直线共有4条。
(2)若AC >BC 且PC BC >(如图2),同(1)有PD 1,PD 2,PD 3。
重庆市2001-2012年中考数学试题分类解析专题9:三角形
一、选择题1. (重庆市2001年4分)如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是【 】.A .带①去B .带②去C .带③去D .带①和②去2. (重庆市2002年4分)如图,⊙O 为△ABC 的内切圆,∠C=90度,OA 的延长线交BC 于点D ,AC=4,CD=1,则⊙O 的半径等于【 】A54 B45 C43 D65【答案】A 。
【考点】三角形的内切圆与内心,相似三角形的判定和性质。
【分析】设圆O 与AC 的切点为M ,圆的半径为r ,如图,连接OM 。
∵∠C=90°,∴CM=r。
∵△AOM∽△ADC,∴OM:CD=AM :AC ,即r:1=(4-r):4,解得r=45。
故选A。
3. (重庆市2003年4分)如图,在△ABC中,∠AED=∠B,DE=6,AB=10,AE=8,则BC的长度为【】A.152B.154C.3 D.834. (重庆市2003年4分)如图所示,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°,②AD∥BC,③PC⊥AB,④四边形ABCD是轴对称图形,其中正确的个数为【】A.1个 B.2个 C.3个 D.4个5. (重庆市2003年4分)如图,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=15,则AD 的长是【 】A B .2 C .1 D .6. (重庆市2004年4分)如图,CD 是平面镜,光线从A 点出发经CD 上点E 反射后照射到B 点,若入射角为α (入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C 、D ,且AC =3,BD =6,CD =11,则tan α的值为【 】A 、311 B 、113 C 、119 D 、9117. (重庆市2004年4分)秋千拉绳长3米,静止时踩板离地面0.5米,某小朋友荡该秋千时,秋千在最高处踩板离地面2米(左右对称),则该秋千所荡过的圆弧长为【 】A 、π米B 、π2米C 、π34米 D 、π23米8. (重庆市大纲卷2005年4分)如图,DE 是△ABC 的中位线,M 是DE 的中点,CM 的延长线交AB 于点N ,则DMN S ∆∶ANMES 四边形等于【 】A 、1∶5 B、1∶4 C、2∶5 D、2∶7 【答案】A 。
2012至2017年广东省中考数学试题分类汇编解直角三角形及应用解答
20、解直角三角形及应用18.(2012广东)如图,小山岗的斜坡AC的坡度是tanα=,在与山脚C距离200米的D 处,测得山顶A的仰角为26.6°,求小山岗的高AB(结果取整数:参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).考点:解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题。
解答:解:∵在直角三角形ABC中,=tanα=,∴BC=∵在直角三角形ADB中,∴=tan26.6°=0.50即:BD=2AB∵BD﹣BC=CD=200∴2AB﹣AB=200解得:AB=300米,答:小山岗的高度为300米.25.(2015)如题25图,在同一平面上,两块斜边相等的直角三角板Rt△ABC与Rt△ADC拼在一起,使斜边AC 完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm.(1) 填空:AD= (cm),DC= (cm);(2) 点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB 上沿A→D,C →B的方向运动,当N点运动到B点时,M,N两点同时停止运动,连结MN,求当M,N点运动了x秒时,点N到AD的距离(用含x的式子表示);(3) 在(2)的条件下,取DC 中点P ,连结MP ,NP ,设△PMN 的面积为y(cm2),在整个运动过程中,△PMN 的面积y 存在最大值,请求出这个最大值.(参考数据:sin75°=,sin15°=)【解析】(1)(2) 如图,过点N 作NE ⊥AD 于E ,作NF ⊥DC 延长线于F ,则NE =DF .∵∠ACD =60°,∠ACB =45°,∴∠NCF =75°,∠FNC =15°,∴sin 15°=FC NC ,又NC =x ,∴FC =,∴NE =DF+.∴点N 到AD+cm ;(3) ∵sin 75°=FN NC ,∴FN =, ∵PD =CP∴PF∴111)222y x x =++-·)即2y =+,当x =时,y有最大值为.20、(2014)如题20图,某数学兴趣小组想测量一棵树CD 的高度,他们先在点A 处测得树顶C 的仰角为30°,然后沿AD 方向前行10m ,到达B 点,在B 处测得树顶C 的仰角高度为60°(A 、B 、D 三点在同一直线上)。
2012年中考数学试题分类解析汇编专题9:三角形
2012年中考数学试题分类解析汇编专题9:三角形一、选择题1. (2012湖北荆门3分)下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是【】A.B.C.D.【答案】B。
【考点】网格问题,勾股定理,相似三角形的判定。
【分析】根据勾股定理,AB=22,BC=2,AC=10,∴△ABC的三边之比为2:22:10=1:2:5。
A、三角形的三边分别为2,10,32,三边之比为2:5:3,故本选项错误;B、三角形的三边分别为2,4,25,三边之比为1:2:5,故本选项正确;C、三角形的三边分别为2,3,13,三边之比为2:3:13,故本选项错误;D、三角形的三边分别为5,13,4,三边之比为5:13:4,故本选项错误.故选B。
2.(2012湖北荆门3分)如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,则PE的长为【】A. 2 B.2C.D.3【答案】C。
【考点】等边三角形的性质,角平分线的定义,锐角三角函数,特殊角的三角函数值,线段垂直平分线的性质。
【分析】∵△ABC是等边三角形,点P是∠ABC的平分线,∴∠EBP=∠QBF=30°,∵BF=2,FQ⊥BP,∴BQ=BF•cos30°=2×3=32。
∵FQ是BP的垂直平分线,∴BP=2BQ=23。
在Rt△BEF中,∵∠EBP=30°,∴PE=12BP=3。
故选C。
3. (2012湖北天门、仙桃、潜江、江汉油田3分)如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC.若△ABC的边长为4,AE=2,则BD的长为【】A.2 B.3 C.3D.3+1【答案】A。
【考点】全等三角形的判定和性质,等腰三角形的性质,平行线分线段成比例,等边三角形的性质。
三年中考2010-2012全国各地中考数学试题分类汇编汇编:直角三角形与勾股定理
2012年全国各地中考数学真题分类汇编第24章直角三角形与勾股定理一.选择题1.(2012•广州)在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是()A.B.C.D.2.(2012毕节)如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E式垂足,连接CD,若BD=1,则AC的长是()A.23B.2C.43D. 43.(2012湖州)如图,在Rt△ABC中,∠ACB=900,AB=10,CD是AB边上的中线,则CD的长是()5A.20B.10C.5D.24.(2012安徽)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是()DA.10B.54C. 10或54D.10或1725. (2012•荆门)下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )A .B .C .D .6. ( 2012巴中)如图3,已知AD 是△ABC 的BC 边上的高,下列能使△ABD≌△ACD 的条件是( )A.AB=ACB.∠BAC=900C.BD=ACD.∠B=450二.填空题7.( 2012巴中)已知a 、b 、c 是△ABC 的三边长,且满足关系c 2-a 2-b 2 +|a-b|=0,则△ABC的形状为______ 8(2012泸州)如图,在△ABC 中,∠C=90°,∠A=30°,若AB=6cm ,则BC= .9.(2012青岛)如图,圆柱形玻璃杯,高为12cm ,底面周长为18cm ,在杯内离杯底4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为 cm.11.(2012南州)如图1,矩形ABCD 中,AB=3,AD=1,AB 在数轴上,若以点A 为圆心,对角线AC 的长为半径作弧交数轴的正半轴于M ,则点M 的坐标为( )A 、(2,0)B 、1,0)C 、)D 、)12.(2012临沂)在Rt△ABC 中,∠ACB=90°,BC=2cm ,CD⊥AB,在AC 上取一点E ,使EC=BC ,过点E 作EF⊥AC 交CD 的延长线于点F ,若EF=5cm ,则AE= cm .13.(2012陕西)如图,从点()02A ,发出的一束光,经x 轴反射,过点()43B ,,则这束光从点A 到点B 所经过路径的长为 .14.(2012•资阳)直角三角形的两边长分别为16和12,则此三角形的外接圆半径是 10或8 .15.(2012无锡)如图,△ABC中,∠ACB=90°,AB=8cm,D是AB的中点.现将△BCD 沿BA方向平移1cm,得到△EFG,FG交AC于H,则GH的长等于 3 cm.16.(2012黔西南州)如图6,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,CE=4,则四边形ACEB的周长为______________.三.解答题17.(2012菏泽)如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1,P2,P3,P4,P5是△DEF边上的5个格点,请按要求完成下列各题:(1)试证明三角形△ABC为直角三角形;(2)判断△ABC和△DEF是否相似,并说明理由;(3)画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△ABC 相似(要求:用尺规作图,保留痕迹,不写作法与证明).2011年全国各地中考数学真题分类汇编第24章直角三角形与勾股定理一、选择题1.(2011山东滨州,9,3分)在△ABC中,∠C=90°, ∠C=72°,AB=10,则边AC的长约为(精确到0.1)()A.9.1B.9.5C.3.1D.3.52. (2011山东烟台,7,4分)如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m和8m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是()A2m B.3mC.6mD.9m3. (2011台湾全区)已知小龙、阿虎两人均在同一地点,若小龙向北直走160公尺,再向东直走80公尺后,可到神仙百货,则阿虎向西直走多少公尺后,他与神仙百货的距离为340公尺?A.100 B.180 C.220 D.2604. (2011湖北黄石,7,3分)将一个有45度角的三角板的直角顶点放在一张宽为3cm的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30度角,如图(3),则三角板的最大边的长为A. 3cmB. 6cmC. 32cmD. 62cm5. (2011贵州贵阳,7,3分)如图,△ABC中,∠C=90°,AC=3,∠B=30°,点P是BC边上的动点,则AP长不可能是(第7题图)(A )3.5 (B )4.2 (C )5.8 (D )76. (2011河北,9,3分)如图3,在△ABC 中,∠C=90°,BC=6,D,E 分别在AB,AC 上,将△ABC 沿DE 折叠,使点A 落在点A ′处,若A ′为CE 的中点,则折痕DE 的长为( )A .21B .2C .3D .4图3A '【答案】B7.8.二、填空题1. (2011山东德州13,4分)下列命题中,其逆.命题成立的是______________.(只填写序号)①同旁内角互补,两直线平行;②如果两个角是直角,那么它们相等;③如果两个实数相等,那么它们的平方相等;④如果三角形的三边长a ,b ,c 满足222a b c +=,那么这个三角形是直角三角形.【答案】① ④2. (2011浙江温州,16,5分)我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1,S2,S3=10,则S2的值是.【答案】1033. (2011重庆綦江,16,4分) 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米. 当正方形DEFH运动到什么位置,即当AE=米时,有DC=AE+BC.14【答案】:34. (2011四川凉山州,15,4分)把命题“如果直角三角形的两直角边长分别为a、b,斜边长为c,那么222+=”的逆命题改写成“如果……,那么……”的形式:a b c。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012中考数学试题及答案分类汇编:三角形2.选择题1. (天津3分)sin45°的值等于(A) 12 (B) 2 (C) 2 (D) 1【答案】B 。
【考点】特殊角三角函数。
【分析】利用特殊角三角函数的定义,直接得出结果。
2.(河北省3分)如图,在△ABC 中,∠C=90°,BC=6,D ,E 分别在 AB 、AC 上,将△ABC 沿DE 折叠,使点A 落在点A′处,若A′为CE 的中点,则折痕DE 的长为A 、B 、2C 、3D 、4【答案】B 。
【考点】翻折变换(折叠问题),相似三角形的判定和性质。
【分析】∵△ABC 沿DE 折叠,使点A 落在点A′处,∴∠EDA=∠EDA′=90°,AE=A′E,∴△ACB∽△AED。
∴ED AE BC AC=。
又∵A′为CE 的中点,∴AE=A′E=A′C 。
∴ED 163=。
∴ED=2。
故选B 。
3.(山西省2分)如图,△ABC 中,AB=AC ,点D 、E 分别是边AB 、AC 的中点,点G 、F 在BC 边上,四边形DEFG 是正方形.若DE=2cm ,则AC 的长为A .B .4cmC ..【答案】D 。
【考点】等腰三角形的性质,三角形中位线定理,正方形的性质,勾股定理。
【分析】根据三角形的中位线定理可得出BC=4,由AB=AC ,可证明BG=CF=1,由勾股定理可求出D 。
4.(内蒙古呼和浩特3分)如果等腰三角形两边长是6cm 和3cm ,那么它的周长是A 、9cmB 、12cmC 、15cm 或12cmD 、15cm【答案】D 。
【考点】等腰三角形的性质,三角形三边关系。
【分析】求等腰三角形的周长,即要确定等腰三角形的腰与底的长,根据三角形三边关系知当6为腰,3为底时,6﹣3<6<6+3,能构成等腰三角形,周长为6+6+3=15;当3为腰,6为底时,3+3=6,不能构成三角形。
故选D 。
5.(内蒙古呼伦贝尔3分)如图,△ACB≌△A 1CB 1, ∠BCB 1=30°,则∠ACA 1的度数为A . 20° B. 30° C. 35° D. 40°【答案】B 。
【考点】全等三角形的性质。
【分析】根据全等三角形对应角相等的性质,得∠ACB=∠A 1CB 1,所以∠ACB-∠BCA 1=∠A 1CB 1-∠BCA 1,即 ∠ACA 1=∠BCB 1=35°。
故选B 。
3.填空题1. (山西省3分)如图,已知AB=12;AB⊥BC 于B ,AB⊥AD 于A ,AD=5,BC=10.点E 是CD 的中点,则AE 的长是 ▲ 。
【答案】132。
【考点】平行的性质,相似三角形的判定和性质,勾股定理。
【分析】过点E 作EG⊥AB,垂足为点G ,AB 与DC 交于点F ,则DA∥GE∥BC。
∵点E 是CD 的中点,AB=12,∴根据平行的性质,得AG=6。
∵DA∥BC,∴△ADF∽△BCF。
∴DA AF CB BF=。
∵AB=12,即BF=12-AF 。
∴DA AF CB 12AF=-。
又∵AD=5,BC=10,∴5AF 1012AF =-,解得,AF=4,FB=8。
FG=6-4=2。
∵GE∥BC,∴△FGE∽△FBC。
∴FG GE FB BC=,即2GE 810=,解得,GE=52。
∴在Rt△AGE 中,由勾股定理,得132=。
2.(内蒙古巴彦淖尔、赤峰3分)如图,AD 是△ABC 的中线,∠ADC=60°,BC=6,把△ABC 沿直线AD 折叠,点C 落在C′处,连接BC′,那么BC′的长为 ▲ .【答案】3。
【考点】翻折变换(折叠问题),轴对称的性质,平角定义,等边三角形的判定与性质。
【分析】根据题意:BC=6,D 为BC 的中点;故BD=DC=3。
由轴对称的性质可得:∠ADC=∠ADC′=60°,∴DC=DC′=2,∠BDC′=60°。
故△BDC′为等边三角形,故BC′=3。
3.(内蒙古巴彦淖尔、赤峰3分)如图,EF 是△ABC 的中位线,将△AEF 沿AB 方向平移到△EBD 的位置,点D 在BC 上,已知△AEF 的面积为5,则图中阴影部分的面积为 ▲ .【答案】10。
【考点】三角形中位线定理,相似三角形的判定和性质,平移的性质。
【分析】∵EF 是△ABC 的中位线,∴EF∥BC,∴△AEF∽△ABC。
∴EF:BC=1:2,∴S △AEF :S △ABC =1:4。
∵△AEF 的面积为5,∴S △ABC =20。
∵将△AEF 沿AB 方向平移到△EBD 的位置,∴S △EBD =5。
∴图中阴影部分的面积为:S △ABC ﹣S △EBD ﹣S △AEF =20﹣5﹣5=10。
4.(内蒙古包头3分)如图,△ABD 与△AEC 都是等边三角形,AB≠AC,下列结论中:①BE=DC;②∠BOD=60°;③△BOD∽△COE.正确的序号是 ▲ . 【答案】①②。
【考点】等边三角形的性质,全等三角形的判定和性质,三角形的内角和定理,相似三角形的判定。
【分析】∵△ABD、△AEC 都是等边三角形,∴AD=AB,AE=AC ,∠DAB=∠CAE=60°。
∴∠DAC=∠BAC+60°,∠BAE=∠BAC+60°。
∴∠DAC=∠BAE。
∴△DAC≌△BAE (SAS )。
∴BE=DC。
【①正确】∴∠ADC=∠ABE。
∵∠BOD+∠BDO+∠DBO=180°,∴∠BOD=180°﹣∠BDO﹣∠DBO=60°。
【②正确】 ∵由△DAC≌△BAE 和AB≠AC,得∠ADC≠∠AEB,∴∠ODB≠∠OEC。
又∵∠ODB<60°,∠OCE>60°,∴∠ODB≠∠OCE。
而∠DOB=∠EOC,∴△BOD 和△COE 不相似。
【③错误】5.(内蒙古呼和浩特3分)如图所示,在梯形ABCD 中,AD∥BC,CE 是∠BCD 的平分线,且CE⊥AB,E 为垂足,BE=2AE ,若四边形AECD 的面积为1,则梯形ABCD 的面积为 ▲ .A D EO【答案】157。
【考点】角平分线和垂直的定义,全等三角形的判定和性质,相似三角形的判定和性质,等腰三角形的判定和性质,三角形的面积,梯形的面积,一元一次方程的应用。
【分析】延长BA与CD,交于F,∵CE是∠BCD的平分线,∴∠BCE=∠FCE。
∵CE⊥AB,∴∠BEC=∠FEC=90°。
∵EC=EC,∴△BCE≌△FCE(ASA)。
∴BE=EF。
∵BE=2AE,∴BF=4AF。
又∵AD∥BC,∴△FAD∽△FBC。
∴2FADFBCS AF1S BF16∆∆⎛⎫=⎪⎝⎭=。
设S△FAD=x,S△FBC=16x,S△BCE=S△FEC=8x,∴S四边形AECD=7x。
∵四边形AECD的面积为1,∴7x=1,∴x=17。
∴梯形ABCD的面积为:S△BCE+S四边形AECD=15x=157。
6.(内蒙古乌兰察布4分)如图,在Rt△ABC中,∠ABC = 900, AB = 8cm , BC= 6cm , 分别以A,C为圆心,以AC2的长为半径作圆, 将 Rt△ABC截去两个扇形,则剩余(阴影)部分的面积为▲cm2(结果保留π)【答案】25244π-。
【考点】直角三角形两锐角的关系,勾股定理,扇形的面积。
【分析】由题意可知,阴影部分的面积为三角形面积减去两个扇形面积。
三角形面积为16824 2=⨯⨯。
由勾股定理,得AC=10,圆半径为5。
∵在Rt△ABC中,∠ABC = 900,∴∠A+∠C =900。
∴两个扇形的面积的和为半径5,圆心角900的扇形的面积,即四分之一圆的面积25 4π。
∴阴影部分的面积为25244π- cm 2。
7.(内蒙古乌兰察布4分)某厂家新开发的一种电动车如图,它的大灯A 射出的光线AB,AC 与地面MN 所夹的锐角分别为 80和 100,大灯A 与地面离地面的距离为lm 则该车大灯照亮地面的宽度BC 是 ▲ m .(不考虑其它因素)【答案】75。
【考点】解直角三角形的应用,锐角三角函数定义。
【分析】过点A 作AD⊥BC,垂足为点D 。
由锐角三角函数定义,得BC =BD -CD =00AD AD 2877AD 71tan8tan10555===⎛⎫--⨯ ⎪⎝⎭。
4.解答题1.(北京5分)如图,点A 、B 、C 、D 在同一条直线上,BE∥DF ,∠A=∠F,AB=FD .求证:AE=FC .【答案】证明:∵BE∥DF,∴∠ABE=∠D。
在△ABC 和△FDC 中ABE D AB FD A F ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC≌△FDC(ASA )。
∴AE=FC.【考点】平行线的性质,全等三角形的判定和性质。
【分析】利用平行线同位角相等的性质可得∠ABE=∠D,由已知用ASA 判定△ABC≌△FDC,再由全等三角形对应边相等的性质证得AE=FC 。
2.(北京5分)如图,在△ABC,AB=AC ,以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ,点F 在AC 的延长线上,且∠CBF=12∠CAB. (1)求证:直线BF 是⊙O 的切线;(2)若AB=5BC 和BF 的长. 【答案】解:(1)证明:连接AE 。
∵AB 是⊙O 的直径,∴∠AEB=90°。
∴∠1+∠2=90°。
∵AB=AC,∴∠1=12∠CAB。
∵∠CBF=12∠CAB,∴∠1=∠CBF。
∴∠CBF+∠2=90°。
即∠ABF=90°。
∵AB 是⊙O 的直径,∴直线BF 是⊙O 的切线。
(2)过点C 作CG⊥AB 于点G 。
∵∠AEB=90°,AB=5在Rt△ABE 中,由勾股定理得 在Rt△CBG 中,可求得GC=4,GB=2,∴AG=3。
∵GC∥BF ,∴△AGC∽△BFA 。
∴GC AG BF AB =。
∴GC AB 20BF AG 3⋅==。
【考点】切线的判定和性质,勾股定理,圆周角定理,相似三角形的判定和性质,解直角三角形。
【分析】(1)连接AE ,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABE=90°。
(2)利用已知条件证得∴△AGC∽△BFA,利用对应边的比求得线段的长即可。
3.(北京5分)阅读下面材料:小伟遇到这样一个问题,如图1,在梯形ABCD 中,AD∥BC,对角线AC ,BD 相交于点O .若梯形ABCD 的面积为1,试求以AC ,BD ,AD+BC 的长度为三边长的三角形的面积.小伟是这样思考的:要想解决这个问题,首先应想办法移动这些分散的线段,构造一个三角形,再计算其面积即可.他先后尝试了翻折,旋转,平移的方法,发现通过平移可以解决这个问题.他的方法是过点D作AC的平行线交BC的延长线于点E,得到的△BDE即是以AC,BD,AD+BC的长度为三边长的三角形(如图2).参考小伟同学的思考问题的方法,解决下列问题:如图3,△ABC的三条中线分别为AD,BE,CF.(1)在图3中利用图形变换画出并指明以AD,BE,CF的长度为三边长的一个三角形(保留画图痕迹);(2)若△ABC的面积为1,则以AD,BE,CF的长度为三边长的三角形的面积等于34.【答案】解:△BDE的面积等于1。
